基于Caputo导数下的含时滞的Hamilton系统的分数阶Noether理论*
丁金凤,金世欣,张 毅
(1.苏州科技大学数理学院,江苏 苏州 215009;2.南京理工大学理学院,江苏 南京 210094;3.苏州科技大学土木工程学院,江苏 苏州 215009)
基于Caputo导数下的含时滞的Hamilton系统的分数阶Noether理论*
丁金凤1,金世欣2,张 毅3
(1.苏州科技大学数理学院,江苏 苏州 215009;2.南京理工大学理学院,江苏 南京 210094;3.苏州科技大学土木工程学院,江苏 苏州 215009)
提出并讨论了Caputo导数定义下的含时滞的Hamilton系统的分数阶Noether对称性与守恒量。 根据含时滞的Hamilton系统的分数阶Hamilton原理,建立了相应的含时滞的分数阶Hamilton正则方程;依据分数阶Hamilton作用量在无限小变换下的不变性,得到了含时滞的Hamilton系统的分数阶Noether对称性;最后,建立了系统的含时滞的分数阶Noether理论,并举例说明结果的应用。
时滞;Hamilton系统;Caputo导数;Noether对称性;守恒量
随着人们认识的深入,发现自然界在本质上是分数阶的,使用分数阶模型能够更好地描述和理解复杂系统的动力学行为及其内在的物理本质,因此分数阶微积分开始广泛应用于力学、物理学、生物学、化学、经济和社会科学,智能控制等领域[1-2]。1996年,Riewe[3-4]首次将分数阶微积分应用到非保守力学建模,开始对于分数阶变分问题的研究近20年来,关于分数阶模型下的变分问题的研究取得了一系列成果[5-11]。Frederico和Torres[12-13]研究了分数阶模型下的分数阶变分与最优化问题的Noether定理。Atanackovi等[14]依据经典的守恒量定义了分数阶守恒量,得到了力学系统的分数阶Noether定理。然而对于分数阶导数下含时滞的变分问题的研究是最近几年才开始的。2008年,Baleanu,Maaraba和Jarad[15-17]首次讨论了分数阶导数下的含时滞的分数阶变分问题,又研究了Caputo分数阶导数下的含时滞的分数阶变分原理,并讨论了含时滞的Caputo分数阶导数下的高阶分数阶变分最优化控制问题。张毅等[18-21]对分数阶导数下非保守力学以及Birkhoff系统动力学的变分问题及其对称性进行了研究,并得到了一些研究成果。本文将进一步研究基于Caputo导数的含时滞的Hamilton系统动力学的分数阶Noether对称性。
1 分数阶导数的定义及其性质
本节列出将要用到的Riemann-Liouville导数以及Caputo导数的定义和性质。详细讨论见文献[1-2]。
左Riemann-Liouville分数阶导数的定义为[5]
(1)
右Remiann-Liouville分数阶导数的定义为
(2)
左Caputo分数阶导数为
(3)
右Caputo分数阶导数为
(4)

(5)
分数阶分部积分公式为
(6)
以及
(7)
其中r∈(t1,t2), 且有
(8)
(9)
2 含时滞的分数阶Hamilton正则方程
假设力学系统由n个广义坐标qs(s=1,2,…,n)来确定。含时滞的分数阶Lagrange函数为
(10)
其中时滞常量τ 引入含时滞的分数阶广义动量和Hamilton函数为 (11) (12) 则对(12)式进行分数阶广义动量进行求导,得到 (13) 非保守系统的分数阶Hamilton原理为 (14) 且满足条件 (15) 其中Ωs(t)为[t1-τ,t1]上的已知分段光滑函数,qs(t2)为已知实数。 类似于文献[20]的推导,由(13)和(14)式,可导出 (16) 联立方程(13)和(16)给出Caputo导数下的含时滞的力学系统的分数阶Hamilton正则方程。 Caputo导数下的含时滞的Hamilton系统的分数阶Hamilton作用量表示为 (17) 其中γ为某已知曲线,引入无限小群变换 (18) 其展开式 (19) (20) (21) 由于 (22) 将式(22)代入式(21),有 (23) 注意到 (24) 以及变换(18)和分部积分公式(6)、(7)、(8)和(9),则式(32)可化为 (25) 其中 (26) 式(23)和式(25)称为Caputo导数下的含时滞的力学系统的分数阶Hamilton作用量变分的基本公式。 如果成立 (27) 则称无限小变换(18)是含时滞的分数阶Noether意义下的对称变换。此时,由式(23)得 当t1≤t≤t2-τ时,有 (28) 当t2-τ (29) 式(28)和(29)可化为,当t1≤t≤t2-τ时,有 (30) 当t2-τ (31) 当r=1时,式(30)和(31)称为含时滞的Hamilton系统的分数阶Noether等式。 如果成立 (32) 其中G=G(t,qs,pαs,ps,qsτ,psτ)为规范函数,则称无限小变换(18)是含时滞的分数阶Noether意义下的准对称变换。此时,由式(23)得 当t1≤t≤t2-τ时,有 (33) 当t2-τ (34) 式(33)和(34)可化表示为,当t1≤t≤t2-τ时,有 (35) 当t2-τ (36) 其中ΔG=εσGσ,当r=1时,式(35)和(36)也称为含时滞的Hamilton系统的分数阶Noether等式。 函数 称为含时滞的力学系统的分数阶守恒量,当且仅当沿着运动方程(13)和(16)的解曲线恒成立 (37) 对于含时滞的分数阶Hamilton系统(13)和(16),如果能找到系统的分数阶Noether对称变换或Noether准对称变换,便可求得相应的分数阶守恒量。于是,有如下定理 定理1 对于含时滞的分数阶Hamilton系统(13)和(16),如果无限小变换(18)是系统的分数阶Noether对称变换,则系统存在r个线性独立的分数阶守恒量,当t1≤t≤t2-τ时,形如 (38) 当t2-τ (39) 证明:将系统的分数阶Hamilton正则方程代入式(25),并考虑到εσ的独立性和积分区间的任意性,当t1≤t≤t2-τ时,得到 (40) 当t2-τ (41) 将式(40)和(41)积分,便得到结果。 定理2 对于含时滞的分数阶Hamilton系统(13)和(16),如果无限小变换(18)是系统的分数阶Noether准对称变换,则系统存在r个线性独立的分数阶守恒量,当t1≤t≤t2-τ时,形如 (42) 当t2-τ (43) 证明:结合式(25)和(32),并利用分数阶正则方程(13)和(16),且考虑到εσ的独立性和积分区间的任意性,即得结论。 定理1和定理2称为含时滞的Hamilton系统的分数阶Noether定理。由分数阶Noether定理可知,对于Caputo导数下的含时滞的Hamilton系统,如果能找到一个含时滞的分数阶Noether对称变换或分数阶Noether准对称变换,便可能得到力学系统的一个分数阶守恒量。 例 已知力学系统的Lagrange函数为 (44) 其中k为常数,时滞常量τ 由式(11)和(12),得到 (45) 则系统的正则方程为 (46) 分数阶Noether等式(35)和(36),得到 (47) 方程(47)有解 (48) (49) 生成元(48)和(49)得到相应于系统的分数阶Noether对称性。由定理1和定理2,得到 const. t1≤t≤t2-τ, const. t2-τ (50) (51) 式(50)和(51)为含时滞的Hamilton系统相应于分数阶Noether对称性(48)和Noether准对称性(49)的分数阶守恒量。 若分数阶导数项不存在时,守恒量(50)和(51)就成为 const. t1≤t≤t2 (52) (53) 式(52)和(53)是含时滞的Hamilton系统的Noether对称性和准对称性的守恒量。如果时滞常量τ不存在,则式(52)和(53)就简化为经典力学系统的守恒量。 本文基于Caputo导数建立了含时滞的Hamilton系统的分数阶Hamilton原理,导出了含时滞的Hamilton系统的分数阶Hamilton正则方程(13)和(16), 得到了含时滞的分数阶Hamilton作用量变分的两个基本公式(23)和(25), 得到了含时滞的分数阶Noether对称性;建立了含时滞的Hamilton系统的分数阶Noether理论。文章的方法和结果具有普遍适用性,可应用于分数阶模型下的含时滞的最优控制系统,也可应用于含时滞的各种约束力学系统。 [1]OLDHAMKB,SPANINERJ.Thefractionalcalculus[M].NewYork:AcademicPress, 1974. [2]PODLUBNYI.Fractionaldifferentialequations[M].SanDiego:AcademicPress, 1999. [3]RIEWEF.Nonconservationlagrangianandhamiltonianmechanics[J].PhysRevE, 1996,53(2): 1890-1899. [4]RIEWEF.Mechanicswithfractionalderivatives[J].PhysRevE, 1997, 55(3): 3581-3592. [5]AGRAWALOP.Formulationofeuler-lagrangeequationsforfractionalvariationalproblems[J].JMathAnalAppl, 2002,272(1): 368-379. [6]BALEANUD,AGRAWALOP.Fractionalhamiltonformalismwithincaputo’sderivative[J].CzechoslovakJPhys, 2006, 56 (10/11): 1087-1092. [7]BALEANUD,TRUJILLOJI.AnewmethodoffindingthefractionalEuler-LagrangeandHamiltonequationswithCaputofractionalderivatives[J].CommunNonlinearSciNumerSimulat, 2010, 15: 1111-1115. [8]ZHANGY.FractionaldifferentialequationsofmotionintermsofcombinedRiemann-Liouvillederivatives[J].ChinPhysB, 2012, 21(8): 084502. [9]LILin,LUOShaokai.FractionalgeneralizedHamiltonianmechanics[J].ActaMech, 2013, 224(8): 1757-1771. [10] 丁金凤,张毅. 基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff变分问题的Noether对称性[J]. 中山大学学报(自然科学版), 2014, 48(6): 829-833. [11] 何胜鑫,朱建青. 基于分数阶模型的相空间中非保守力学系统的Noether对称性[J].中山大学学报(自然科学版), 2015, 54(4): 37-42. [12]FREDERICOGSF,TORRESDFM.Noether’stheoremforfractionaloptimalcontrolproblems[J].Math, 2006, 2(1):74-89. [13]FREDERICOGSF,TORRESDFM.Fractionalconservationlawsinoptimalcontroltheory[J].NonlinearDyn, 2008, 53(3): 215-222. [14]ATANACKOVITM,KONJIKS,SIMIS.Variationalproblemswithfractionalderivatives:InvarianceconditionsandNoether’stheorem[J].NonlinearAnal, 2009, 71(5/6): 1504-1517. [15]JARADF,ABDELJAWADT,BALEANUD.FractionalvariationalprincipleswithdelaywithinCaputoderivatives[J].MathPhys, 2010, 1(65): 17-28. [16]JARADF,ABDELJAWADT,BALEANUD.Fractionalvariationaloptimalcontrolproblemswithdelayedargument[J].NonlinearDyn, 2010, 62 (3): 609-614. [17]JARADF,ABDELJAWADT,BALEANUD.Higherorderfractionalvariationalandoptimalcontrolproblemswithtimedelay[J].ApplMathCom, 2012, 218(2): 9234-9240. [18]ZHAIXH,ZHANGY.NoethersymmetriesandconservedquantitiesforfractionalBirkhoffiansystems[J].NonlinearDyn, 2014, 77(1): 73-86. [19]JINSX,ZHANGY.Noethersymmetriesfornon-conservativeLagrangesystemswithtimedelaybasedonfractionalmodel[J].NonlinearDyn, 2015, 79: 1169-1183. [20]JINSX,ZHANGY.Noethertheoremfornon-conservativesystemswithtimedelayinphasespacebasedonfractionalmodel[J].NonlinearDyn, 2015, 82: 663-676. [21] 金世欣,张毅.基于Caputo分数阶导数的含时滞的非保守系统动力学的Noether对称性[J].中山大学学报(自然科学版), 2015, 54(5): 49-55. Fractional Noether theorems for Hamilton system with time delay based on Caputo dervitaves DINGJinfeng1,JINShixin2,ZHANGYi3 (1. College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China;2. College of Physics, Nanjing University of Science and Technology, Nanjing 210018, China;3. College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215009, China) The fractional Noether symmetries and fractional conserved quantities for Hamilton system with time delay based on Caputo derivatives are discussed. The fractional Hamilton canonical equations of the corresconding system with time delay are established base upon the fractional Hamilton principle of the Hamilton systems with time delay. Then, the fractional Noether symmetries of the Hamilton system with time delay are obtained, which based on the invariance of the fractional Hamilton action with time delay under the infinitesimal transformations of group. Finally, fractional Noether theorems with time delay of the Hamilton system are established. At the end, one example is given to illustrate the application of the results. time delay; Hamilton system; Caputo derivatives; Noether symmetry; conserved quantity 10.13471/j.cnki.acta.snus.2016.06.012 2016-05-12 国家自然科学基金资助项目(10972151,11272227) 丁金凤(1983年生),女;研究方向:力学中的数学方法;E-mail:vividding@126.com O A 0529-6579(2016)06-0079-073 含时滞的Hamilton系统的分数阶Noether对称性



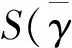





4 含时滞的Hamilton系统的分数阶Noether理论






5 算 例

6 结 论

