焊接H形截面钢柱板组弹塑性相关屈曲和容许宽厚比

邓长根　 张晨辉　 周　江

(同济大学土木工程学院, 上海 200092)

焊接H形截面钢柱板组弹塑性相关屈曲和容许宽厚比

邓长根 张晨辉 周江

(同济大学土木工程学院, 上海 200092)

摘要:建立了竖向轴压力和单调水平荷载作用下焊接H形截面悬臂钢柱板组弹塑性相关屈曲的有限元分析模型,通过改变轴压比、翼缘宽厚比、腹板高厚比及翼缘-腹板厚度比等参数,对非特厚实截面钢柱进行几何非线性和材料非线性有限元分析.然后,基于分析结果,利用最小相对误差拟合法得到极限弯矩比的实用计算公式.最后,基于整体-局部等稳原则导出板组容许宽厚比相关曲线方程,并通过算例对容许宽厚比相关曲线与钢结构设计规范的翼缘和腹板宽厚比限值曲线进行比较.结果表明:构件长细比较小时,规范规定的翼缘和腹板宽厚比限值可能超出容许宽厚比相关曲线限定的范围;翼缘宽厚比与腹板高厚比限值相关,并且两者均随轴压比、翼缘-腹板厚度比、构件长细比、塑性发展系数的变化而变化.

关键词:焊接H形截面;局部相关屈曲;弹塑性;极限弯矩比;宽厚比限值

H形截面构件由平板组成,在压力和弯矩作用下可能出现构件整体失稳和板件局部失稳的情况.板件局部失稳不仅会降低构件的极限承载力,还会局限截面塑性发展,降低构件的抗震延性和耗能能力.因此,设计H形截面压弯钢构件时,需要限制板件的宽厚比,使板件的屈曲应力不低于构件整体的屈曲应力或钢材的屈服强度,防止板件发生局部屈曲,从而提高构件的极限承载力、抗震延性和耗能能力.我国2003版钢结构设计规范[1]按照等稳原则(板件屈曲应力等于构件整体屈曲应力)确定板件宽厚比限值,而新版钢结构设计规范[2]和欧洲钢结构设计规范[3]则依据等强原则(板件屈曲应力等于钢材屈服强度),先确定板件屈服宽厚比,再乘以不同的折减系数,来确定不同等级(S1,S2,S3,S4[2])或不同类别(第1,2,3,4类[3])截面的板件界限宽厚比.这些规范的共同点在于,均采用单一板件原则[4]确定宽厚比限值,或忽略板件间的相互作用,或利用固定的约束系数或嵌固系数近似考虑翼缘对腹板的约束作用,翼缘宽厚比限值与腹板高厚比限值之间不存在显式的耦合关系.

然而,组成构件的板件稳定性有强弱之分,板件屈曲时会产生相关作用,且板件屈曲后仍存在相关性,计算构件极限承载力时应考虑这种相关性[5].各种型钢截面(包括H形截面)的板件弹性相关屈曲研究结果表明,板件弹性屈曲系数与板件宽厚比及相邻板件宽厚比相关[6],即翼缘屈曲与腹板屈曲之间存在明显的耦合关系.因此,确定板件宽厚比限值时应考虑翼缘与腹板的相关屈曲,翼缘屈曲与腹板屈曲的耦合关系无法用某些固定的约束系数或嵌固系数来表示.H形(或I形)轴压构件、压弯构件的弹塑性局部相关屈曲及局部-整体相关屈曲研究结果表明,翼缘宽厚比限值与腹板高厚比限值之间存在相互耦合关系[7-9].文献[8]研究了H形截面钢构件不同延性等级截面的转动能力,采用椭圆标准方程来表示翼缘宽厚比限值与腹板高厚比限值之间的相互耦合关系;日本旧版钢结构极限状态设计指南[10]中,H形截面翼缘宽厚比限值与腹板高厚比限值采用了类似的椭圆相关公式;然而,这些椭圆相关公式尚未体现轴压比的影响,无法应用于轴压比较大的压弯构件.文献[9]研究了H形截面钢梁-柱构件的极限承载力和塑性变形能力,并给出了极限弯矩比和延性系数的计算公式,其中正则化宽厚比由翼缘宽厚比限值与腹板高厚比限值的类似椭圆相关公式演变而来,相当于椭圆缩小比例系数;这些公式反映了梁-柱轴压比、剪-弯应力比、弯矩梯度等参数的影响,体现了翼缘宽厚比与腹板高厚比的耦合关系,依据日本新版钢结构极限状态设计指南[11],可确定不同延性等级截面的翼缘宽厚比限值与腹板高厚比限值相关曲线.

本文通过对焊接H形截面钢柱在竖向轴压力和单调水平荷载作用下进行非线性有限元分析,考察了轴压比、翼缘宽厚比、腹板高厚比及翼缘-腹板厚度比等参数对构件弹塑性局部相关屈曲极限弯矩比的影响;在参数分析的基础上,拟合得到极限弯矩比的实用计算公式;基于等稳原则推导出板组容许宽厚比相关曲线方程,并通过算例揭示了我国钢结构设计规范中翼缘宽厚比和腹板高厚比限值存在的局限性,分析各参数对容许宽厚比相关曲线的影响.

1板组弹塑性相关屈曲有限元分析

1.1钢柱受力及加载模式

对于竖向重力荷载和水平地震共同作用下的钢框架,钢柱同时承受轴压力、水平地震剪力和绕截面强轴弯矩,2层以上钢柱的反弯点可近似假设在钢柱中点处.从钢框架中提取反弯点以下半层高为L的悬臂钢柱作为计算模型(见图1),钢柱受竖向轴压力Nn和水平荷载F作用,下端梁柱连接处点o可简化为固定端,上端反弯点可简化为悬臂端.图中,Δ为悬臂端水平位移;θ=Δ/L为层间位移角.

图1　荷载和位移简图

本文对图1中钢柱在给定竖向轴压力Nn和单调水平荷载F作用下的板组弹塑性相关屈曲性能进行了研究.首先,施加竖向轴压力N到给定值Nn,然后单调增大水平位移Δ(相应的水平荷载为F),直至构件产生足够大的变形.钢柱底部绕强轴弯矩M=FL,考虑板组弹塑性相关屈曲效应的极限荷载(即F-Δ曲线上F的极大值)为Fu,极限弯矩Mu=FuL.

1.2钢柱基本参数和正则化参数

本文中钢采用双轴对称H形截面(见图2).图中,bf,tf分别为翼缘宽度和翼缘厚度;h,tw分别为腹板(名义)高度和厚度;fy,fwy分别为翼缘、腹板的钢材屈服强度.当H形截面钢柱绕强轴压弯时,板件宽厚比组配和轴压比为影响其极限承载力和延性的主要因素[12].令翼缘宽厚比rf=0.5bf/tf,腹板高厚比rw=h/tw,翼缘-腹板厚度比rt=tf/tw.

图2　H形截面及残余应力分布图

为便于将研究结果扩展至其他钢材,定义如下正则化参数:轴压比n=Nn/Np,弯矩比φ=M/Mp.其中,Np=2Affy+Awfwy,Af,Aw分别为单块翼缘截面积和腹板截面积;Mp为不考虑轴力作用、仅在绕强轴弯矩作用下的截面塑性极限弯矩.考虑板组弹塑性相关屈曲效应的极限弯矩比φu=Mu/Mp,简称为(局部稳定)极限弯矩比.

选取翼缘宽厚比等级和腹板高厚比等级组配在S2级～S5级[2]之间的非特厚实截面,各参数的取值范围如下:10.000≤rf≤18.333,52.0≤rw≤84.5,1.25≤rt≤2.00,n=0.1～0.6,L=1.5m.

1.3有限元分析模型

采用ANSYS软件建立焊接H形截面钢柱(压弯构件)的有限元模型(见图3).选用4节点、支持初应力功能的SHELL181单元,沿截面板件宽度和构件轴向进行均匀网格划分;选择合适的等分数,保证计算结果的准确性与精度.固定端约束所有6个自由度;为了控制构件长细比,避免构件发生整体失稳,悬臂端约束弯矩作用平面外位移Uz与绕截面弱轴y和绕构件轴线x的转动自由度Ry和Rx.钢材采用理想弹塑性本构模型,弹性模量E=2.06×105MPa,Q235钢材屈服强度fy=fwy=235MPa,泊松比ν=0.3.采用一致缺陷模态法引入几何缺陷,按图4所示的压弯构件一阶屈曲模态施加板组的初始鼓曲变形,其峰值取bf/100[13];引入图2所示的残余应力模式(轧制边或剪切边)[14],假定残余应力沿构件轴向不变.

图3　有限元模型及约束条件

图4　一阶屈曲模态

1.4弹塑性局部相关屈曲极限承载力

先施加轴压力Nn于悬臂端,再分级增大水平位移Δ,进行几何非线性和材料非线性分析,跟踪构件平衡路径(即跟踪F-Δ曲线),越过平衡路径极值点(相应荷载为极限荷载Fu),直至构件产生足够大的变形.由F-Δ曲线可得到φ-θ曲线,从系列φ-θ曲线中提取不同参数对应的极限弯矩比φu,则可绘出极限弯矩比φu与计算参数的相关曲线.改变轴压比、翼缘宽厚比、腹板高厚比及翼缘-腹板厚度比等参数,对不同压弯荷载作用下的系列焊接H形截面钢柱进行几何非线性和材料非线性有限元分析.将板组弹塑性相关屈曲导致钢柱达到承载能力极限状态的有限元分析结果作为有效分析结果.

2极限弯矩比相关曲线及拟合公式

改变轴压比n、翼缘宽厚比rf、腹板高厚比rw及翼缘-腹板厚度比rt,对系列焊接H形截面钢柱进行板组弹塑性相关屈曲极限承载力非线性有限元分析,分别考察这些参数对钢柱极限弯矩比的影响.

当rt=1.5,rw=72.0,rf=13.333,15.000时,极限弯矩比与轴压比的相关曲线见图5.

当rt=1.5,n=0.2,0.4,rw=52.0,59.5,72.0,84.5时,极限弯矩比与翼缘宽厚比的相关曲线见图6.

图5　极限弯矩比与轴压比的相关曲线

(a) n=0.2

(b) n=0.4

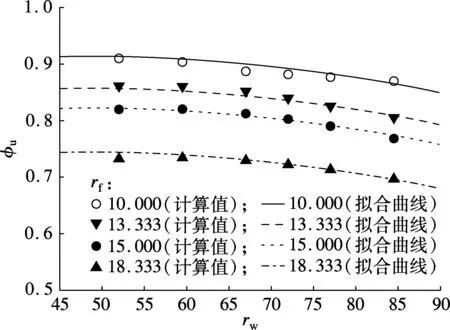
当rt=1.5,n=0.2,0.4,rf=10.000,13.333,15.000,18.333时,极限弯矩比与腹板高厚比的相关曲线见图7.

当rf=11.667,13.333,15.000,16.667,rw=59.5,72.0,n=0.2,0.4时,极限弯矩比与翼缘-腹板厚度比的相关曲线见图8.

由图5～图8可知,随着轴压比、翼缘宽厚比的增大,极限弯矩比显著降低;随着腹板高厚比的增大,极限弯矩比也降低,但影响不如翼缘宽厚比明显;翼缘-腹板厚度比对极限弯矩比也有影响,但影响不显著.

根据极限弯矩比的变化规律,利用关于参数n,

(a) n=0.2

(b) n=0.4

rf,rw,rt的二次多项式,拟合得到极限弯矩比φu的实用计算公式.进一步将腹板高厚比rw和翼缘宽厚比rf进行正则化处理,即

(1)

式中,λw,λf分别为正则化腹板高厚比和翼缘宽厚比;rwy,rfy分别为四边简支矩形板、三边简支一边自由矩形板在单向均匀压力作用下屈曲的弹性极限宽厚比.

利用最小相对误差拟合法,得到极限弯矩比φu的正则化实用计算公式(简称拟合公式):

φu=φu(λw,λf,rt,n)=0.883+0.246λw+0.197λf+

0.167rt-n(0.891+0.264λw+0.096λf-

(2)

拟合公式(2)的相对误差为±2.54%,拟合参数范围为52.0≤rw≤84.5,10.000≤rf≤18.333,0.1≤n≤0.6,1.25≤rt≤2.00.

极限弯矩比φu的拟合曲线与有限元计算点对比如图5～图8所示.由图可知,拟合公式与有限元计算点吻合良好,且变化趋势一致,可适当将拟合公式的适用参数范围拓宽为40≤rw≤100,8≤rf≤20,0.05≤n≤0.65,1.00≤rt≤2.25.采用正则化参数λw,λf,n后,拟合公式(2)可适当扩展至其他钢材,而不仅限于Q235钢材.

(a) n=0.2,rw=59.5

(b) n=0.4,rw=59.5

(c) n=0.2,rw=72.0

(d) n=0.4,rw=72.0

3板组容许宽厚比相关曲线

3.1平面内稳定板组容许宽厚比相关曲线

根据等稳原则,同时满足压弯构件平面内整体稳定性和局部相关稳定性要求,推导腹板高厚比限值与翼缘宽厚比限值的相关曲线方程.

利用压弯构件平面内整体稳定性验算公式[2]近似计算平面内整体稳定性极限弯矩时,采用钢材屈服强度替换钢材设计强度f,得到压弯构件平面内整体稳定性极限弯矩为

(3a)

(3b)

根据拟合公式(2),得到考虑板组弹塑性相关屈曲效应的极限弯矩Mu=φuMp=φuγpfyW1x.令Mu=Mxu,导出平面内等稳方程为

(4)

(5)

对于H形截面无侧移框架柱和两端支承的压弯构件[2],等效弯矩系数βmx=0.6+0.4M2/M1,其中M1,M2为端弯矩;当悬臂端弯矩M2=0时,βmx=0.6.设翼缘和腹板均为Q235钢材,取γx=1.05,rt=1.0,1.5,2.0.当n=0.4,λx=70和n=0.3,λx=80时,平面内稳定板组容许宽厚比相关曲线与按照我国钢结构设计规范[1-2]及日本钢结构极限状态设计指南[10-11]得到的板组宽厚比限值曲线(即腹板高厚比限值和翼缘宽厚比限值曲线)对比见图9.由图可知,当n=0.4,λx=70时,新版规范中S4,S3级截面和2003版规范中的翼缘宽厚比限值超越了容许宽厚比相关曲线的限定范围;当n=0.3,λx=80时,新版规范中S4级截面和2003版规范中的腹板高厚比限值和翼缘宽厚比限值均超越了容许宽厚比相关曲线的限定范围.在适当范围内调整轴压比n、厚度比rt和长细比λx,进行更多算例分析,同样可发现新版规范和2003版规范的腹板高厚比限值和翼缘宽厚比限值可能超越容许宽厚比相关曲线的限定范围,表明构件在丧失平面内整体稳定性之前会先发生弹塑性局部相关屈曲.此外,我国钢结构设计规范[1-2]未考虑板组相关屈曲,故板组宽厚比限值曲线中出现了阶跃突变;日本钢结构极限状态设计指南[10-11]中考虑了板组相关屈曲,故板组宽厚比限值曲线连续光滑,且变化趋势与板组容许宽厚比相关曲线的变化趋势吻合,由此可知,按日本钢结构极限状态设计指南[10-11]确定的板组宽厚比限值曲线更加合理.

(a) n=0.4,λx=70

(b) n=0.3,λx=80

图9　平面内稳定容许宽厚比相关曲线及板组宽厚比限值曲线

由图9(b)还可看出,翼缘-腹板厚度比rt对容许宽厚比相关曲线有较大影响,rt减小时容许宽厚比相关曲线向外扩展;当腹板高厚比rw=50～60时,翼缘容许宽厚比达到极大值,在其达到极大值之前(即腹板高厚比rw<50时),腹板高厚比越小则翼缘容许宽厚比越小.根据日本钢结构极限状态设计指南[10-11]中的椭圆相关公式,腹板高厚比越小则翼缘容许宽厚比越大,这与上述容许宽厚比相关曲线变化趋势截然相反.

当长细比λx和轴压比n均较小时,即使厚度比rt、腹板高厚比rw、翼缘宽厚比rf及其他参数在适当范围内变化,平面内等稳方程(4)仍无解,表明构件的局部相关稳定性弱于平面内整体稳定性,构件先发生弹塑性局部相关屈曲.

当塑性发展系数γx=1.05时,具有不同轴压比n和厚度比rt的构件的容许宽厚比相关曲线见图10.结合平面内等稳方程(4)可知,一般情况下,n增大,容许宽厚比相关曲线向外扩展,宽厚比限值放松;rt增大,容许宽厚比相关曲线的扩展方向不确定,受其他参数取值影响.

当塑性发展系数γx=1.05时,具有不同长细比λx的构件的容许宽厚比相关曲线见图11.结合平面内等稳方程(4)可知,一般情况下,λx减小,容许宽厚比相关曲线向里收缩,宽厚比限值更加严格.

进一步考察平面内等稳方程(4)发现,等效弯矩系数βmx对H形截面构件平面内稳定容许宽厚比相关曲线影响较大.特别是βmx取较小值甚至最小值0.2时,对钢柱的局部稳定性不利.当钢柱两端弯矩反号时,应预防最大弯矩区域发生弹塑性局部相关屈曲.

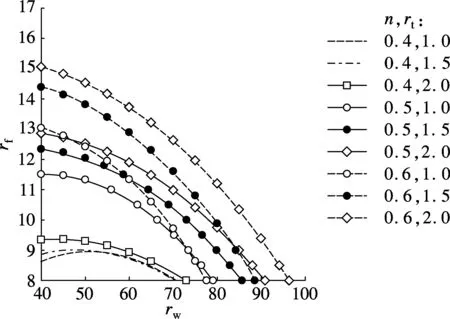
(a) λx=60

(b) λx=80

(a) n=0.3,rt=1.5

(b) n=0.4,rt=1.5

3.2平面外稳定板组容许宽厚比相关曲线

根据等稳原则,同时考虑压弯构件平面外整体稳定性和局部相关稳定性要求,推导腹板高厚比限值与翼缘宽厚比限值的相关曲线方程.

利用压弯构件平面外整体稳定性验算公式[2]近似计算平面外整体稳定性极限弯矩时,采用钢材屈服强度替换钢材设计强度f,得到压弯构件平面外整体稳定性极限弯矩为

(6)

式中,λy为弯矩作用平面外长细比;φy=φy(λy)为焊接H形截面(翼缘为轧制或剪切边)绕弱轴的轴心受压构件(c类)稳定系数;φb=φb(λy)为双轴对称H形截面受弯构件整体稳定系数.

(7)

对于H形截面压弯构件,设翼缘和腹板均为Q235钢材,取γx=1.05,rt=1.0,1.5,2.0.当n=0.1,λy=30和n=0.5,λy=40时,平面外稳定板组容许宽厚比相关曲线与按照我国钢结构设计规范[1-2]及日本钢结构极限状态设计指南[10-11],得到的板组宽厚比限值曲线对比见图12.

由图12可知,当n=0.1,λy=30时,我国新版规范中S4级截面的腹板高厚比限值和翼缘宽厚比限值部分超越了rt=1.5,2.0时的容许宽厚比相关曲线的限定范围;新版规范中S3,S2,S1级截面与2003版规范的腹板高厚比限值和翼缘宽厚比限值在容许宽厚比相关曲线限定范围内.当n=0.5,λy=40时,新版规范中S4,S3,S2,S1级截面与2003版规范的腹板高厚比限值和翼缘宽厚比限值在容许宽厚比相关曲线限定范围内.由此表明,当轴压比较小、弯矩作用平面外长细比较小时,新版规范的腹板高厚比限值可能导致构件发生弹塑性局部屈曲.

4试验验证拟合公式及有限元分析

(a) n=0.1,λy=30

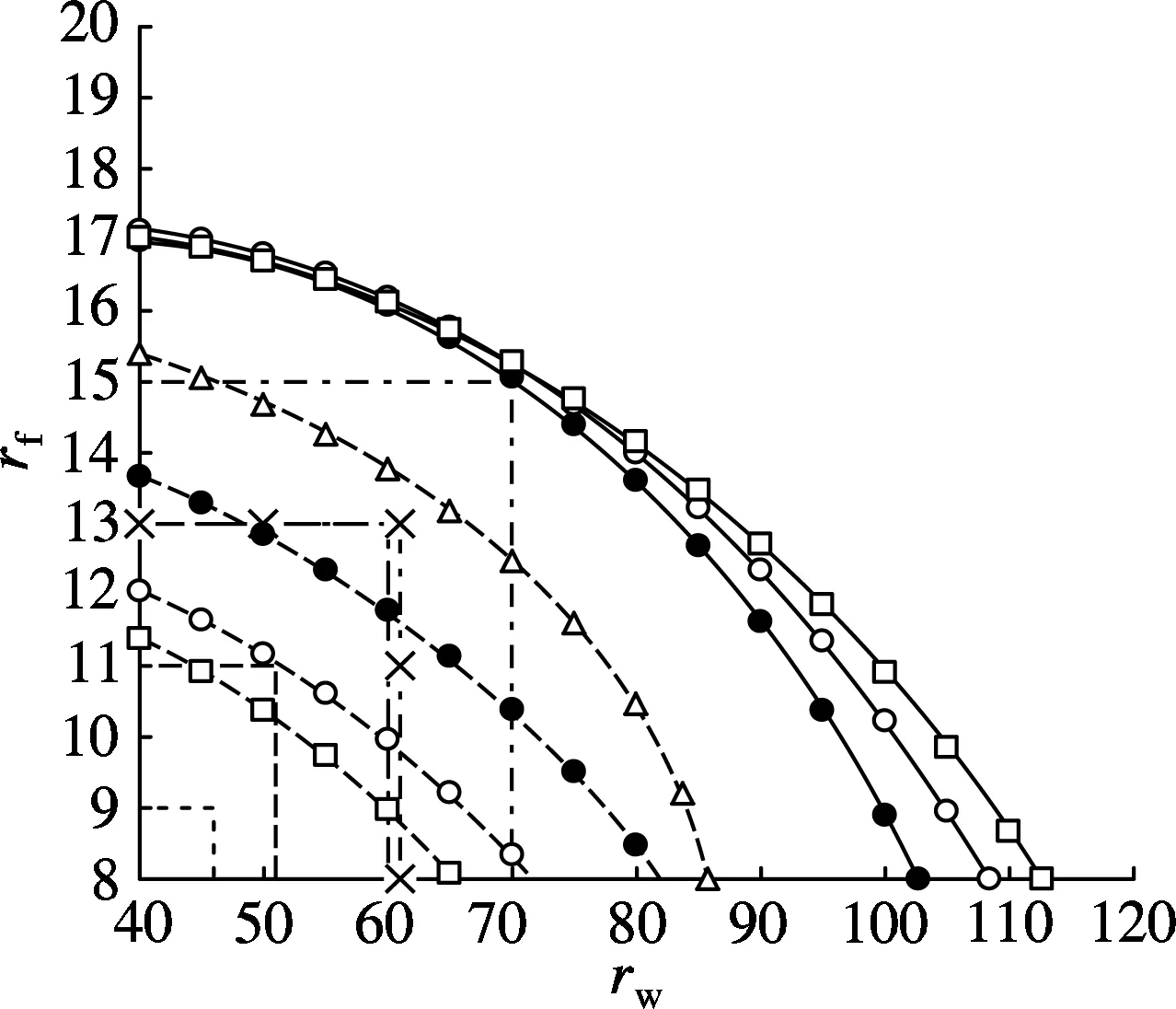
(b) n=0.5,λy=40

图12　平面外稳定容许宽厚比相关曲线及板组宽厚比限值曲线

试件编号H1H2H3H4H5H6h/mm293291292293339295bf/mm159.8156157.5198.8158.5156.5tw/mm6.145.645.065.045.205.10tf/mm7.645.795.805.787.745.74fwy/MPa283.08283.08369.23369.23369.23369.23fy/MPa260.08283.08283.08283.08260.08283.08腹板等级S1S1S3S3S3S4翼缘等级S3S4S4S5S2S4Nn/kN200.4171.5157.9180.5198.8315.8n0.1750.1760.1490.1510.1540.297Meu/(kN·m)153.59114.89126.15131.22192.51103.74Mu/(kN·m)125.3397.0298.06104.70147.9174.59Mfu/(kN·m)119.5292.52100.02106.24149.5878.33Mxu/(kN·m)161.87136.53135.94164.84188.98105.61eM/%-4.64-4.642.001.471.135.01

试件H1的腹板等级为S1级,翼缘等级为S3级,其试验和有限元分析破坏变形模式见图13.由图可知,受压一侧翼缘与腹板以一个屈曲半波的形式明显鼓曲,表明局部相关屈曲导致构件达到承载能力极限.其他5个试件的试验和有限元分析破坏变形模式与试件H1类似.

(a) 试验照片

5结论

1) 随着轴压比、翼缘宽厚比、腹板高厚比的增大,焊接H形截面钢柱的极限弯矩比均降低;轴压比、翼缘宽厚比的影响比腹板高厚比的影响更显著.翼缘-腹板厚度比对钢柱的极限弯矩比也有一定影响,但影响不显著.

2) 拟合得到的极限弯矩比实用计算公式最大相对误差为±2.54%,精度较高,但偏于保守,适用范围可适当从Q235钢材扩展到其他钢材,且不会引起很大误差.

3) 我国2003版钢结构设计规范及新版钢结构设计规范中S4,S3级截面的腹板高厚比限值和翼缘宽厚比限值都可能超越容许宽厚比相关曲线限定的范围,S2级、S1级截面翼缘宽厚比限值也可能超越容许宽厚比相关曲线限定的范围.

4) 在一定条件下,翼缘容许宽厚比达到极大值,在其达到最大值之前,翼缘容许宽厚比随着腹板高厚比减小而略有减小.因此,以往研究中腹板高厚比越小则翼缘容许宽厚比越大的结果可能是片面的,腹板高厚比较小时,根据椭圆相关公式得到的翼缘宽厚比限值可能偏大.

5) 为避免板件局部失稳先于平面内整体失稳发生,一般情况下,构件长细比和轴压比越小,塑性发展系数越大,板组宽厚比限值应越严格.

6) 等效弯矩系数取较小值甚至最小值0.2时,对钢柱的局部稳定性不利,当钢柱两端弯矩反号时,应预防最大弯矩区域发生弹塑性局部相关屈曲.

参考文献 (References)

[1]中华人民共和国建设部.GB50017—2003钢结构设计规范[S].北京:中国计划出版社,2003.

[2]《钢结构设计规范》国家标准管理组.GB50017—201X钢结构设计规范(报批稿)[S].(待出版)

[3]EuropeanCommitteeforStandardization.EN1993-1-1Eurocode3:Designofsteelstructures,part1.1:Generalrulesandrulesforbuildings[S].Brussels:EuropeanCommitteeforStandardization, 2005.

[4]ChenYY,ChengX,NethercotDA.Anoverviewstudyoncross-sectionclassificationofsteelH-sections[J]. Journal of Constructional Steel Research, 2013, 80: 386-393.DOI:10.1016/j.jcsr.2012.10.006.

[5]陈绍蕃.冷弯型钢板件相关屈曲和极限承载力[J].建筑钢结构进展,2002,4(1):3-6.DOI:10.3969/j.issn.1671-9379.2002.01.001.

ChenShaofan.Plateinteractivebucklingandultimate

capacityofcold-formedsections[J]. Progress in Steel Building Structures, 2002, 4(1): 3-6.DOI:10.3969/j.issn.1671-9379.2002.01.001.(inChinese).

[6]SeifM,SchaferBW.Localbucklingofstructuralsteelshapes[J]. Journal of Constructional Steel Research, 2010, 66(10): 1232-1247.

[7]ShokouhianM,ShiYJ.ClassificationofI-sectionflexuralmembersbasedonmemberductility[J]. Journal of Constructional Steel Research, 2014, 95: 198-210.DOI:10.1016/j.jcsr.2013.12.004.

[8]KatoB.RotationcapacityofH-sectionmembersasdeterminedbylocalbuckling[J]. Journal of Constructional Steel Research, 1989, 13(2/3): 95-109.

[9]HasegawaR,IkarashiK.StrengthandplasticdeformationcapacityofH-shapedbeam-columns[C]//IABSE Symposium Report, IABSE Madrid Symposium: Engineering for Progress, Nature and People.Zurich,Switzerland:InternationalAssociationforBridgeandStructuralEngineering, 2014, 102: 579-586.DOI:10.2749/222137814814028223.

[10]日本建築学会.鋼構造限界状態設計指針[S].東京：日本建築学会,1990.

[11]日本建築学会.鋼構造限界状態設計指針[S].東京：日本建築学会,2010.

[12]程欣,陈以一.考虑板件相关作用的H形截面压弯钢构件抗弯承载力[J].工程力学,2015,32(3):41-49.

ChengXin,ChenYiyi.MomentresistanceofH-sectionsteelbeam-columnsconsideringtheinteractiveeffectofplaneelements[J]. Engineering Mechanics, 2015, 32(3): 41-49. (inChinese)

[13]中华人民共和国建设部.GB50205—2001钢结构工程施工质量验收规范[S].北京:中国计划出版社,2001.

[14]周江.焊接H型截面钢构件弹塑性相关屈曲试验与有限元分析[D].上海:同济大学土木工程学院,2012.

Elasto-plasticinteractivebucklingandallowablewidth-thicknessratiosofplateassemblyinweldedH-sectionsteelcolumns

DengChanggenZhangChenhuiZhouJiang

(CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)

Abstract:The finite element analysis model was built for the elasto-plastic interactive buckling of plate assembly in a welded H-section cantilevered steel column subjected to the vertical axial compressive force and the horizontal monotonic shear force. A series of geometrical and material nonlinear finite element analyses for steel columns with non-plastic sections were carried out by varying the axial compression ratio, the flange width-thickness ratio, the web height-thickness ratio, and the flange-web thickness ratio. Then, the practical formula of the ultimate moment ratio was obtained by the minimum relative error fitting algorithm based on the analysis results. Finally, the equation for the allowable width-thickness ratio correlation curves of plate assembly was derived on the basis of the principle of simultaneous overall and local interactive buckling. And the allowable width-thickness ratio correlation curves were compared with the flange and web width-thickness ratio limitation curves according to Code for Design of Steel Structures. The results show that the width-thickness ratio limitations of the flange and the web according to the code may exceed the regions enclosed by the allowable width-thickness ratio correlation curves when the slenderness ratio is small. The flange width-thickness ratio is relative to the web height-thickness ratio limitations, and both of them vary with the changes of the axial compression ratio, the flange-web thickness ratio, the member slenderness ratio, and the plasticity development coefficient.

Key words:welded H-section; local interactive buckling; elasto-plasticity; ultimate moment ratio; width-thickness ratio limitation

DOI:10.3969/j.issn.1001-0505.2016.03.012

收稿日期:2015-07-28.

作者简介:邓长根(1962—)，男，博士，教授，博士生导师，dengcg@tongji.edu.cn.

基金项目:国家自然科学基金重点资助项目(51038008)、国家自然科学基金资助项目(51478330).

中图分类号:TU391

文献标志码:A

文章编号:1001-0505(2016)03-0523-09

引用本文: 邓长根,张晨辉,周江.焊接H形截面钢柱板组弹塑性相关屈曲和容许宽厚比[J].东南大学学报(自然科学版),2016,46(3):523-531.DOI:10.3969/j.issn.1001-0505.2016.03.012.