图上具有可变指数反应项的波动方程解的爆破
许 璐,辛 巧
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
图上具有可变指数反应项的波动方程解的爆破
许璐,辛巧
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
[摘要]本文利用能量方法,讨论带有可变指数反应项的波动方程解的爆破性质,并给出解的爆破时间的上界估计。
[关键词]波动方程;爆破;变指数;反应项
偏微分方程解的爆破现象及其解的渐近行为是偏微分方程研究的重要内容,而其爆破行为存在于非常多类型的偏微分方程,如Schrödinger方程、半线性热传导方程、多孔介质方程、Ginzburg-Landau方程和波动方程[1-3].图上的偏微分方程可以看作连续型的偏微分方程的数值模拟,应用于图像处理、分子扰动和动力系统等领域[4-5],对其解的渐近行为的研究已得到了国内外越来越多学者的关注[6-10].本文主要讨论如下图上具有可变指数反应项的波动方程解的爆破行为和爆破时间的上界估计.
(1)
其中,初值条件u1(x),u2(x)≥0,并且不恒等于零.
在文献[11]中,作者引入了图上微积分,并讨论其上的调和方程的性质及其反传导问题.设G表示一个有限、简单、连通图,其中V=S∪∂S表示图G顶点的集合,S和∂S是顶点集V的两个不相交的子集,分别称为V的内部和边界;E表示图G的边集;ω∶V×V→[0,+∞)表示定义在图G边上的权重函数,且满足:(a)对于任意的x∈V,有ω(x,x)=0;(b)对于任意的x,y∈V,若x~y,则有ω(x,y)=ω(y,x)>0;(c)边(x,y)∉E,则有ω(x,y)=0.其中x~y表示图G的顶点x,y存在一条边,也可表示为(x,y)∈E.

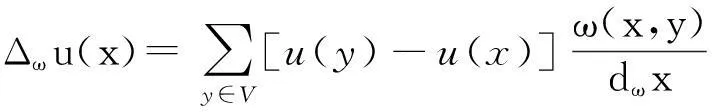
本文中关于图上的函数的积分和ω-Laplacian算子的定义和符号主要参考文献[10].
下面讨论解的爆破性质,在此之前,先给出两个引理.
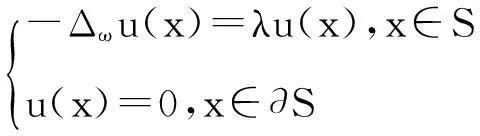
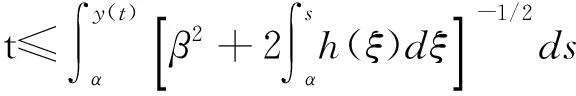

证明设η(t)=∫x∈Suφ,由格林公式可得
η″(t)=∫x∈Suttφ=∫x∈SφΔωu+∫x∈Sφup(x)=-λ1η+∫x∈Sφup(x).
(2)
下面讨论上述等式的第二项∫x∈Sφup(x).
对于任意固定的t>0,设Su≥1={x|x∈S,u(x,t)≥1} ,Su<1={x|x∈S,u(x,t)<1},则有
∫x∈Sφup(x)=∫Su≥1φup(x)+∫Su<1φup(x)≥∫Su≥1φup-
=∫Su≥1φup-+∫Su<1φup--∫Su<1φup-
(3)
=∫Sφup--∫Su<1φup-≥∫Sφup--N.
此外,由Jensen不等式,可知

(4)
联合不等式(2)、(3)、(4)可知
η″(t)≥-λ1η+cηp--N.
(5)
其中,c是正常数,N=|S|表示图G内部顶点的个数.
因为η(0)=∫x∈Su1φ>0,η′(0)=∫x∈Su2φ>0.此外,由于p->1,当η(0)足够大时,可使-λ1η(0)+cηp-(0)-N>0.如果再假设函数h(s)=-λ1s+csp--N,容易验证,当s≥η(0)时,h(s)单调递增,即知s≥η(0),有h(s)>0.综上可知,微分不等式(5)满足引理2的条件,由引理2可知η′(t)>0,且t≤

另一方面,还有η(t)=∫x∈Suφ≤‖u(x,t)‖∞∫x∈Sφ=‖u(x,t)‖∞,所以u(x,t)在有限时间爆破.
综上所述,本文讨论了图上的带有可变指数反应项的波动方程解的爆破行为,得到了解的爆破时间的上界估计.事实上,本文的方法还可以用于带有非局部项的波动方程解的爆破研究.
[参考文献]
[1]Hu B.Blow-up Theories for semilinear Parabolic Equations[M].Berlin Heidelberg:Springer-Verlag,2011.
[2]Llanos M P, Rossi J D. Blow-up for a non-local diffusion problem with Neumann boundary conditions and a reaction term [J].Nonlinear Analysis:ATM,2009,70(4):1629-1640.
[3]Pinasco J P. Blow-up for parabolic and hyperbolic problems with variable exponents[J].Nonlinear Anal:ATM, 2009,71(3-4):1094-1099.
[4]Chung S Y,Chung Y S,Kim J H.Diffusion and elastic equations on networks[J].Publ Res Inst Math Sci,2007, 43(3):699-725.
[5]Trinajstic N,Babic D,Nikoli S.The Laplacian matrix in chemistry[J].J Chem Inf Comput Sci,1994,34(2):368-376.
[6]Zakrzewski W J.Laplacians on lattices[J].J Nonlinear Math Phys,2005,12(4):530-538.
[7]Elmoataz A,Lezoray O,Bougleux S.Nonlocal discrete regularization on weighted graphs:a framework for image and manifold processing[J].IEEE Tans Image Process,2008,17(7):1047-1060.
[8]Xin Q,Xu L,Mu C L.Blow-up for the ω-heat equation with dirichlet boundary conditions and a reaction term on graphs[J].Appl Anal,2013,93(8):1691-1701.
[9]Chung S Y. Critical blow-up and global existence for discrete nonlinear p-Laplacian parabolic equations[J]. Disc Dyna Nat Soc,2014:1-10.
[10]Zhou W C,Chen M M,Liu W J.Critical exponent and blow-up rate for the ω-diffusion equations on graphs with dirichlet boundary conditions[J].Elec J Diff Equa 2014:1-13.
[11]Chung S Y,Berenstein C A.ω-Harmonic function and inverse conductivity problems on networks[J].SIAM J Appl Math,2005,56(4):1200-1226.
[12]Chung F R K.Spectral graph theory[M].Providence:American Mathematical Society,1997.
Blow-up of the Wave Equation with Variable Source on Finite Graphs
XU Lu, XIN Qiao
(College of Mathematics and Statistics, Yili Normal University, Yining Xinjiang 835000, China)
Abstract:By the energy method, we mainly discuss the blow-up of the wave equation with variable source, and also give the upper bound of the blow-up time.
Key words:wave equation; blow-up; variable exponent; reaction term
[收稿日期]2016-03-07
[基金项目]新疆维吾尔自治区自然科学基金项目“图上的偏微分方程解的性质研究”(201442137-30)。
[作者简介]许璐(1986- ),女,助教,硕士,从事偏微分方程理论研究。
[通讯作者]辛巧(1981- ),男,副教授,博士,从事偏微分方程及其应用研究。
[中图分类号]O175
[文献标识码]A
[文章编号]2095-7602(2016)06-0006-03

