基于改进高斯-牛顿迭代法的吊杆参数识别

杨吉新,周兴宇,刘前瑞

(1.武汉理工大学 交通学院，湖北 武汉　430063; 2.中国市政工程中南设计研究总院有限公司，浙江 杭州　310009)



基于改进高斯-牛顿迭代法的吊杆参数识别

杨吉新1,周兴宇1,刘前瑞2

(1.武汉理工大学 交通学院，湖北 武汉430063; 2.中国市政工程中南设计研究总院有限公司，浙江 杭州310009)

摘要：文章针对目前振动频率法在系杆拱桥吊杆索力测试中存在的不足，依据吊杆两端简支并考虑其抗弯刚度的模型，以计算长度、抗弯刚度、吊杆索力为参数进行参数灵敏度分析，利用改进的高斯-牛顿迭代法对抗弯刚度及计算长度进行迭代识别，以梅山南路桥施工监控为背景，将识别得到的吊杆索力值与有限元模型计算所得的理论值比较。结果表明，该迭代算法在吊杆参数识别中收敛速度快、精度高，修正了由于简化复杂边界条件给两端简支模型带来的误差，满足系杆拱桥在施工和运营期间索力测试的精度要求。

关键词：吊杆；灵敏度；迭代法；参数识别

0引言

吊杆是钢管混凝土系杆拱桥重要的传力构件,工程中常用的吊杆索力测定方法主要有千斤顶法、压力传感器法和振动频率法[1]。

千斤顶法适用于张拉过程中的索力测量,其值可通过油压表读数经过标定公式换算得到;压力传感器法须在锚垫板下安装压力环,且不可拆卸,因而费用较为昂贵;振动频率法所采用设备体积小、测量过程简单及频率测量精度高,可以对已张拉完成的吊杆进行复测[2]。

因而,振动频率法在目前工程实践中得到广泛应用。在钢管混凝土拱桥中,吊杆边界条件比较复杂,选取不同的简化模型利用振动频率法将得到不同的索力值。

文献[3]假设理想的弦两端固定,不计吊杆的抗弯刚度,则关系式为

(1)

其中,T为吊杆索力;m为吊杆单位长度质量;fn为振动频率,n为振动阶次;l为吊杆计算长度。

文献[4]基于(1)式,并计入抗弯刚度得到关系式为

(2)

其中,EI为吊杆的抗弯刚度。

文献[5]将吊杆两端的边界条件视为固结,同时考虑吊杆抗弯刚度的影响,得到一个超越方程,利用数值分析拟合出经验公式。文献[6]考虑复杂边界条件,如减震器的影响等,通过理论分析得到同时包含频率、索力的隐式表达式。

实际工程中,上述4种算法均存在不足之处。第1种方法未考虑抗弯刚度的影响,当吊杆振动阶次较高时,计算所得的索力存在较大的误差[7];第2、第3种方法虽然考虑抗弯刚度的影响,但由于吊杆中钢丝之间结合程度未知,在实际工程中很难得到抗弯刚度的准确数值[8];第4种方法全面地考虑吊杆边界条件,但其包含边界条件较多,对各影响边界条件的参数精度要求较高。

笔者在六安市梅山南路桥施工监控期间发现,由于吊杆安装过程中会存在一定的位置偏差,导致张拉过后,吊杆会偏向预埋件边缘而挤压减震器,因而,无法确定减震器各项实际参数。

鉴于上述原因,结合实际监控项目,若要利用振动频率法准确测得吊杆索力,必须找到对实测频率影响较大的参数,然后对其进行有效地识别,从而提高实际测试精度。

1吊杆参数灵敏度分析

1.1吊杆灵敏度分析方法

考虑吊杆的抗弯刚度,由结构动力学基本原理,建立吊杆自由振动方程[9]为

其中,y(x,t)为吊杆在横向振动的位移。

该式求解复杂,根据文献[10]得到

(4)

根据(4)式进行灵敏度分析,讨论吊杆固有频率对各参数的灵敏程度。

(4)式可简单地表示为

(5)

对于(5)式这类显式表达式,可对其求导得到各参数灵敏度表达式,即

(6)

其中,i取值为1,2,3。

对(4)式求导,可以得到fn对T、EI、l的灵敏度表达式,即

(7)

1.2吊杆参数灵敏度分析工程实例

六安市梅山南路桥是一座斜靠式钢管混凝土拱桥,其计算跨径为92 m,桥面宽为51 m。全桥共有60根吊杆,其中主拱、斜拱分别设置15对吊杆,吊杆顺桥向间距均为5 m,具体布置如图1所示,该桥吊杆共分2次张拉。

图1　梅山南路桥主拱吊杆布置图

选取8根长度不同的吊杆,分别命名为S1～S8,结合S7进行灵敏度分析。

经计算，其吊杆第1次张拉力为1 434 kN,单位长度质量为35.28 kg/m,抗弯刚度为273.7 kN·m2(取同等直径下钢柱的抗弯刚度),吊杆两端锚垫板之间的距离为21.647 m。将相关数据代入(4)、(7)式,结果如图2、图3、图4所示。

图2　频率阶次对吊杆索力的灵敏度

图3　频率阶次对吊杆抗弯刚度的灵敏度

图4　频率阶次对吊杆长度的灵敏度

由图2、图3、图4可以看出:

(1) 当固有频率的阶数比较低时,频率对吊杆索力的灵敏度随阶数的增加而增加,当固有频率的阶数较高时,其灵敏度值随阶数的增加而趋于稳定。

(2) 频率对吊杆抗弯刚度的灵敏度随着频率阶数的增加而增加。此外,当阶数较高时,其灵敏度值增加更迅速,表明利用频率法间接测量索力时,若主振动频率的阶数较高时,抗弯刚度对索力的贡献将会变大。

(3) 频率对吊杆长度的灵敏度随着频率阶数的增加而增加,但其灵敏度值为负,当阶数较高时,其值增加更迅速,吊杆的计算长度对吊杆索力的影响也就越大。

(4) 对于索力,频率对吊杆抗弯刚度以及吊杆长度的灵敏度较高。同一振动阶次时,频率对吊杆长度的灵敏度最大。鉴于此,为保证测量精度,有必要对吊杆抗弯刚度及吊杆长度这2个重要参数进行识别。

在2次张拉过程中,实际测得的频率阶次具有偶然性,这增加了参数识别的难度以及工作量。为解决这一问题,可利用改进高斯-牛顿迭代法进行计算。

2基于改进迭代法的吊杆参数识别原理

对于某根吊杆,单位长度质量为已知量,抗弯刚度、吊杆计算长度为待识别参数,固有频率为自变量,其值用动测仪测得,索力为因变量。则吊杆张力T与EI、 l、f之间的关系可用函数关系表示为

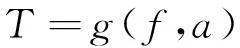
(8)

其中,f是单个变量,a=(a1,a2)=(EI, l)。

由动测仪读数可以测得不同吊杆索力下的吊杆固有振动频率f1、f2,由千斤顶油表读数可以测得2次张拉过程中的张拉力T1、T2。根据2现场实际观测值(fk,Tk)(k=1,2),可以利用迭代法识别出EI、l参数。改进的高斯-牛顿迭代法[11]迭代步骤如下:

(9)

(10)

(11)

由(11)式可以得到

(12)

(13)

(2) 求迭代矩阵,即

(14)

其中,n1为第1次张拉测得固有频率对应的阶数；n2为第2次张拉测得固有频率对应的阶数。

考虑到JTJ可能会出现病态,即通过JTJ迭代可能会导致迭代过程无法收敛,现引入阻尼因子λ,求出JTJ+λI。

(15)

(3) 求εi,即

(16)

继而根据(9)式算出ai值。

(5) 在迭代过程中,若发现εi值趋向于下降时,则适当减小阻尼因子λ值。反之,在迭代过程中若发现εi值趋向于上升时,则适当增加阻尼因子λ值。

结合梅山南路桥施工监控中现场实测数据,利用此法进行迭代计算,验证此算法的可行性。

3改进的高斯-牛顿迭代法应用

梅山南路桥吊杆张拉分2次进行,采用JMM-268动测仪测得2次张拉时的吊杆振动频率,并读取千斤顶油压表读数。

选取3种不同长度的吊杆(S2、S6、S8),利用改进的高斯-牛顿迭代法算法对其进行参数识别。2次张拉过程中,各吊杆实测数据见表1所列。

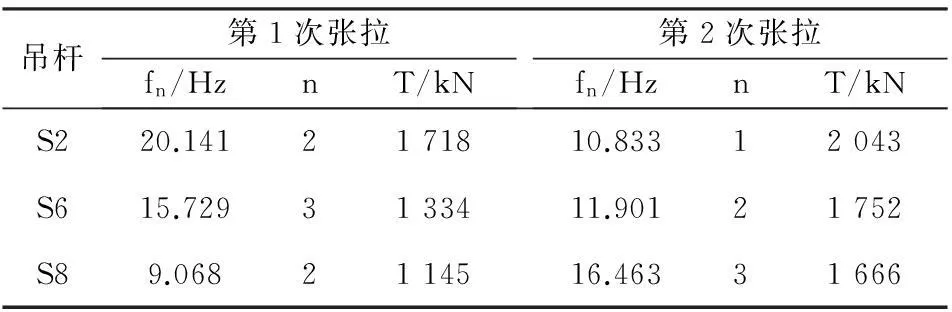
表1　吊杆实测数据表

本例中,对S2,EI0取140 kN·m2,l0取10 m,λ取0.001。将各初始数据输入到Mat lab,经过迭代后得到l、EI的识别值分别为11.148 m、190.9 kN·m2。S2、S6、S8各参数识别结果见表2所列。

表2　吊杆参数识别表

由表2可知,利用该算法可以在考虑测量误差的情况下,准确地识别出利用(4)式计算系杆拱桥吊杆索力的吊杆计算长度及抗弯刚度。同时可发现,利用此法计算时,随着吊杆实际锚固长度的增加,吊杆计算长度逐渐接近于锚垫板之间的长度,即随着吊杆长度的增加,边界条件的变化对吊杆索力的测试影响越来越小。随着吊杆长度的增加,所识别出来的抗弯刚度逐渐变小,表明抗弯刚度的影响越来越小。

在施工阶段2次张拉过程中,分别对其中16根吊杆(由于主拱、斜拱均为对称结构,吊杆也对称布置,故全桥共有16根长度不同的吊杆)利用此法进行计算长度及抗弯刚度识别,将识别出的参数分别代入公式中,以便于在张拉完成之后成桥状态下的索力测试工作。由于篇幅有限,本文仅列出半跨主拱共计8根吊杆的参数识别数据及实测索力等,结果见表3所列。

表3　各吊杆参数识别结果及实测索力

表3中,T为现场实测值,T0为成桥状态下,即在第2次张拉完成、桥下落架之后的理论值,该值经过建立有限元模型计算所得。

由表3可以看出,根据实测吊杆振动频率,利用此法得到的吊杆索力值与理论值误差在±6%之内。鉴于该桥工况较多、工艺复杂且存在一定的测量误差,可以认为其吻合度较好,能够满足工程精度要求。

4结论

针对目前振动频率法在钢管混凝土拱桥索力测试中存在的问题,本文对梅山南路桥吊杆进行参数灵敏度分析,然后利用改进的高斯-牛顿迭代法识别出吊杆计算长度及抗弯刚度的2个主要参数。

(1) 对于钢管混凝土拱桥中的吊杆,固有振动频率对吊杆计算长度最为敏感,抗弯刚度次之。在工程实践中,为保证得到较为精确的索力值,需要对吊杆计算长度及抗弯刚度进行识别。

(2) 利用改进的高斯-牛顿迭代法进行吊杆参数识别,通过引入阻尼因子参数,能够有效地避免迭代过程中不收敛情况的发生,极大地提高迭代效率。同时,将迭代后识别出的抗弯刚度及吊杆计算长度,利用(4) 式计算得到的索力与理论值吻合较好,修正了由于公式未考虑吊杆两端边界条件的复杂情况所带来的误差。

〔参考文献〕

[1]王荣辉，薛礼建.矮塔斜拉桥索力测试方法研究[J].中外公路, 2011, 31(2):116-120.

[2]吴晓亮.频率法在钢管混凝土吊杆拱桥索力测试中的研究与应用[D].合肥：合肥工业大学，2010.

[3]Taehyo P，Do H L，Byeong H K. Estimation of tension force in double hangers by a system identification approach[J]. Inverse Problems in Science and Engineering,2010,18(2):197-216.

[4]张戎令，杨子江，朱学辉，等.基于频率计算系杆拱桥吊杆张拉力的实用公式[J].西南交通大学学报(自然科学版),2015,50(5):823-829.

[5]安振源，宋一凡，刘国，等.刚性短索索力的实用测试方法研究[J].公路工程,2009,34(5):46-50.

[6]何容，陈淮，何伟.考虑复合边界条件的中、下承式拱桥吊杆张力计算公式[J].中国铁道科学,2012,33(5):15-21.

[7]赵瑞鹏.悬索桥索力测试分析研究[J].公路交通科技,2015(10):170-172.

[8]陈彦江，程建旗，闫维明，等.基于参数灵敏度分析的吊杆索力识别[J].振动与冲击,2011,30(7):256-260.

[9]雷凡.带减振器的斜拉桥索力测试方法的理论与试验研究[D].武汉：武汉理工大学,2007.

[10]方志，汪建群，颜江平.基于频率法的拉索及吊杆张力测试[J].振动与冲击, 2007,26(9):78-82.

[11]张鸿燕，耿征. Levenberg-Marquardt算法的一种新解释[J].计算机工程与应用,2009,45(19):5-8.

收稿日期：2016-04-05；修改日期：2016-04-12

基金项目：安徽省高校自然科学研究资助项目(KJ2016A448)

作者简介：杨吉新(1964-)，男，湖南永州人，博士，武汉理工大学教授．

中图分类号：U448.25

文献标识码：A

文章编号：1673-5781(2016)02-0145-04