竞争物种的分数阶对流-弥散方程组的有限元方法

吴红英

(怀化学院 数学与计算科学学院,湖南 怀化　418008)



竞争物种的分数阶对流-弥散方程组的有限元方法

吴红英

(怀化学院 数学与计算科学学院,湖南 怀化418008)

摘要：描述种群增长的分数阶偏微分方程组一般没有解析解，有限元方法是进行数值模拟的有效途径.针对两个竞争物种的非线性分数阶对流-弥散方程组，先进行时间半离散,然后运用压缩映射原理证明变分解的局部存在唯一性,同时给出求解有限元解的一种迭代算法.数值实例表明三次有限元迭代算法的时空收敛阶分别为1和4.

关键词：对流-弥散方程组;分数微分算子;存在唯一性;迭代算法

1引言

考虑非线性空间分数阶微分方程组:

(1.1)

(1.2)

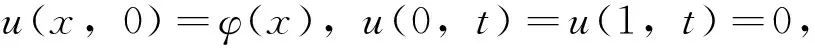
(1.3)

(1.4)

其中0<βi<1(i=1,2),D,K>0,r∈R,(x,t)∈Ω×T,Ω=(0,1),T=(0,T).空间分数导数定义如下:

(1.5)

上述偏微分方程组在人口增长模型中有许多应用(文献[5-7]).一般地,u和v表示两个竞争种群密度,r表示出生率,D为弥散系数,K为环境容量.如果hi(x,t)≡0,系统是封闭的,u,v随时间自主发展,不受外界影响.文献[8-10]研究了分数微分方程解的存在唯一性和在计算物理中的一些实际应用;文献[1,3,4,6,8,11-13]讨论了数值解的实现，但都是基于线性方程(组)或单个非线性方程的.由于分数积分的复杂性,对模型(1.1)-(1.4)不论是解析解的研究还是数值解的实现都具有一定挑战性.

2存在唯一性定理

定义时间剖分

(2.1)

(2.2)

这里

记μi=1-βi/2(i=1,2),定义双线性形式:

+((σ1-r+σ2v)u,φ),∀u,φ∈Hμ1(Ω),

+((σ1-r+σ2u)v,φ),∀v,φ∈Hμ2(Ω),

其中(·,·)为L2(Ω)空间上的内积,<·,·>μi为Hμi(Ω)和H-μi(Ω)空间上的偶对.对充分大的σ1,上述双线性形式满足强制性和连续性(Ervin和Roop[2]).给定fn∈H-μ1(Ω),gn∈H-μ2(Ω),定义线性泛函

从而(2.1)(2.2)的Galerkin变分解定义如下:寻找u∈Hμ1(Ω),v∈Hμ2(Ω)使得

(2.3)

(2.4)

上述变分方程组问题是半线性的，其解的存在性还未见相关文献讨论.通常处理非线性问题总是需要假设fn,gn满足Lipchitz条件,本问题显然不满足.我们设计一种迭代算法，将方程组进行线性化处理，再运用Ervin和Roop关于线性问题的存在唯一性结果证明(2.3)-(2.4)的存在唯一性.

假设:假定Δtn充分小,从而σ1充分大使得下列条件满足

(2.5)

(2.6)

(2.7)

其中M1,M2由(2.11)式定义.

定理:在条件(2.5)-(2.7)下,变分问题(2.3)-(2.4)存在唯一解u∈Hμ1(Ω),v∈Hμ2(Ω).

证明:运用压缩映射原理证明.定义有界闭集

(2.8)

其中C1,C2为双线性强制常数,与u,v无关.取(u(0),v(0))∈S,定义映射

T1∶Hμ1(Ω)→Hμ1(Ω)

u(i)→u(i+1),i=0,1,…

T2∶Hμ2(Ω)→Hμ2(Ω)

v(i)→v(i+1),i=0,1,…

满足

(2.9)

(2.10)

接下来分三步证明.

第1步：序列(u(i),v(i))∈S.由于σ1充分大,双线性B1,v(i)和B2,u(i)中u,v的系数为正,根据Ervin和Roop的讨论，上述映射T1,T2确实存在.另外有限元解u(i),v(i)有界,即

上式表明(u(i),v(i))∈S对所有i成立.同时注意到μi>1/2(i=1,2),由Sobolev不等式存在正常数M1,M2使得

(2.11)

几乎处处成立.

第2步：序列(u(i),v(i))按L2范数收敛.由(2.9)式有

从而

(2.12)

进一步变形得

(2.13)

令φ=u(i+1)-u(i)并注意到B1(u(i+1)-u(i),u(i+1)-u(i))≥0,

故

(2.14)

与(2.14)类似,关于v有

(2.15)

结合(2.14)，(2.15)及假设条件(2.7)有

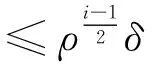
(2.16)

(2.17)

(2.18)

(2.19)

(2.20)

综合(2.18)，(2.20)知变分问题(2.3)，(2.4)存在唯一解u=limi→∞u(i),v=limi→∞v(i),且u∈L2(Ω),v∈L2(Ω).

第3步：序列(u(i),v(i))按Hμi(Ω),(i=1,2)范数收敛.令φ=u(i+1)-u(i)代入(2.13)并注意到σ1-r-σ2v(i)≥σ1-r-|σ2|M2≥0,

(2.21)

运用B1,v(i)的强制性定理，方程两边同时约去‖u(i+1)-u(i)‖L2(Ω)得

(2.22)

再应用(2.19)式有

(2.23)

(2.24)

采用相同的方法可证明

(2.25)

综合(2.24)，(2.25)知变分问题(2.3)，(2.4)存在唯一解u=limi→∞u(i),v=limi→∞v(i),且u∈Hμ1(Ω),v∈Hμ2(Ω).定理证毕.

注解:在上述证明过程中,必须通过缩小实间步长Δtn使得(2.5)-(2.7)3个条件同时成立.换言之,变分解的存在唯一性关于时间是局部的,要得到全局存在性必须附加其它条件,例如解的一致有界性.事实上证明过程给出了一个有限元求解的迭代算法,而(2.5)-(2.7)正是迭代算法收敛的充分条件,ρ的大小决定迭代解收敛到解析解的速率.

迭代算法:设V为分段连续的m次多项式有限元空间(关于分数微分方程有限元方法的实现见参考文献[11]),迭代算法如下:

第2步：for i=0:TolN分别求解线性有限元方程(2.9)和(2.10);

l=i+1;退出循环;

end

3数值实例

我们采用三次有限元方法验证算法的有效性.取模型参数D=r=K=1,β=0.2,p=1,q=0,T=1,令

可以验证u(x,t)=t2x2(1-x),v(x,t)=t3x3(1-x)是系统方程(1.1)-(1.2)的精确解.收敛阶按如下公式计算：

表-1列出了固定空间步长Δx和时间步长Δt的误差和收敛阶.数值结果显示随着时间和空间步长的逐步缩小，有限元解uh,vh确实收敛到精确解u,v，时空收敛阶大约为1和4,说明算法有效.

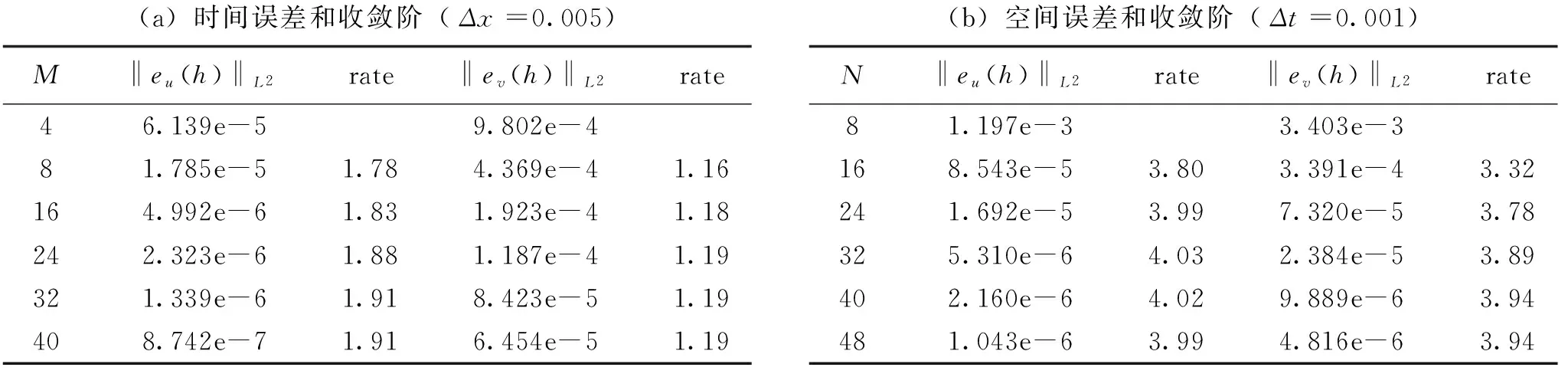
表1　有限元数值结果误差分析

参考文献：

[1]G.J.Fix,J.P.Roop,Least squares finite-element solution of a fractional order two-point boundary value problem[J].Comput.Math.Appl,2004(28):1017-1033.

[2]V.J.Ervin,J.P.Roop.Variational formulation for the stationary fractional advection dispersion equation[J].Numer.Methods Partial Differential Equations,2006(22):558-576.

[3]V.J.Ervin,J.P.Roop.Variational solution of fractional advection dispersion equations on bounded domains in Rd[J].Numer.Methods Partial Differential Equations,2007(23):256-281.

[4]V.J.Ervin,N.Heuer,J.P.Roop.Numerical approximation of a time dependent nonlinear,space-fractional diffusion equation[J].SIAMJ.Numer.Anal,2007(45):572-591.

[5]B.Baeumer,M.Kovács,M.M.Meerschaert.Fractional reproduction-dispersal equations and heavy tail dispersal kernels[J].Bull.Math.Biol,2007(69):2281-2297.

[6]B.Baeumer,M.Kovács,M.M.Meerschaert.Numerical solutions for fractional reaction-di.usion equations[J].Comput.Math.Appl,2008(55):2212-2226.

[7]M.Kirane,Y.Laskri,N.Tatar.Critical exponents of Fujita type for certain evolution equations and systems with spatio-temporal fractional derivatives[J].J.Math.Anal.Appl,2005(312):488-501.

[8]H.Brunner,L.Ling,M.Yamamoto.Numerical simulations of 2D fractional subdiffusion problems[J].J.Comput.Phys,2010(229):6613-6622.

[9]Alberto Cabada,Zakaria Hamdi.Nonlinear fractional differential equations with integral boundary value con-ditions[J].Applied Mathematics and Computation,2014(228):251-257.

[10]Ali Yakar,Mehmet Emir Koksal.Allaberen Ashyralyev,Existence Results for Solutions of Nonlinear Fractional Differential Equations[J].Abstractand Applied Analysis,2012.

[11]周志强,吴红英.分数阶对流-弥散方程的移动网格有限元方法[J].数值计算与计算机应用,2014(1):1-7.

[12]陈一鸣,刘丽丽,孙璐,等.Adomian分解法求解非线性分数阶Fredholm积分微分方程[J].应用数学,2013(4):785-790.

[13]周志强,吴红英.基于Grüwald-Letnikov定义的分数导数数值算法[J].怀化学院学报,2010(5):1-4.

Finite Element Solution to Fractional Advection-Dispersion Modle with Two Species

WU Hong-ying

(DepartmentofMathematics,HuaihuaUniversity,Huaihua,Hunan418008)

Abstract：Nonlinear space-fractional differential equations(SFDEs)have more and more important applications in population growth model of biology.In this article a time semi-discrete formula and an iteration algorithm for SFDEs are presented.Using fixed point theorem,existence and uniqueness results for corresponding variable problems are proven in fractional derivative spaces.Numerical example illustrates the FEM iteration algorithm has first and fourth convergence rate for time and space,respectively.

Key words：advection-dispersion equations；fractional differential operations;existence and uniqueness;iteration algorithm

收稿日期：2015-11-28

作者简介：吴红英，1974年生，女，湖南张家界人，副教授，研究方向：拓扑学与数值计算.

中图分类号：O175.14；O175.22

文献标识码：A

文章编号：1671-9743(2016)05-0010-05