三维重构系统的极线矫正算法研究
唐 彬,金晅宏
(上海理工大学 光电信息与计算机工程学院,上海 200093)
三维重构系统的极线矫正算法研究
唐彬,金晅宏
(上海理工大学 光电信息与计算机工程学院,上海 200093)
摘要在设计三维重构系统的过程中发现,极线矫正算法的优劣将直接关系到三维重构结果的准确性和精确度。因此,文中采用了先进行控制点变换再进行灰度值插值的算法来达到极线矫正的目的。该方法通过控制点变换来定义空间变换本身,用其来描述每个像素如何从初始位置"移动"到终止位置,再利用灰度值插值算法产生一个光滑映射,并将像素点的灰度值改变,从而达到矫正的目的。文中不仅对矫正前后左右目摄像头采集到的图像进行了对比,还对右图矫正前后的灰度波形进行了对比,矫正后的图像整体向左平移了150个像素点。
关键词极线矫正;控制点变换法;双线性插值法
极线矫正是数字图像处理中的重要技术之一[1]。如图1所示,极线矫正的目的是将原像点投影到一个虚拟像面上,使得对应极线共线且与图像坐标轴平行[2],从而简化立体匹配过程,提高匹配速度和精度。由于极平面可以用向量T和向量P表示,根据向量的乘法运算有[3]
(P-T)·(T×P)=0
(1)
目前较常用的图像矫正方法有透视变换法和控制点变换法,透视变换法主要是依据摄像机成像原理,实现图像矫正;而控制点变换方法的主要原理是依据控制点的对应关系,用双线性插值的方法实现图像矫正[4]。
1极线矫正的前提条件
在进行极线矫正之前,首先要对摄像机进行标定或者弱标定[5]。已知空间某一点P在世界坐标系和相机图像坐标系下的齐次坐标分别是W=(XW,YW,ZW,1)T和m=(u,v,1)T,于是有
(2)
式中,s为比例系数;A为相机内部参数矩阵;P和T分别为世界坐标系到相机坐标系的旋转和平移向量。
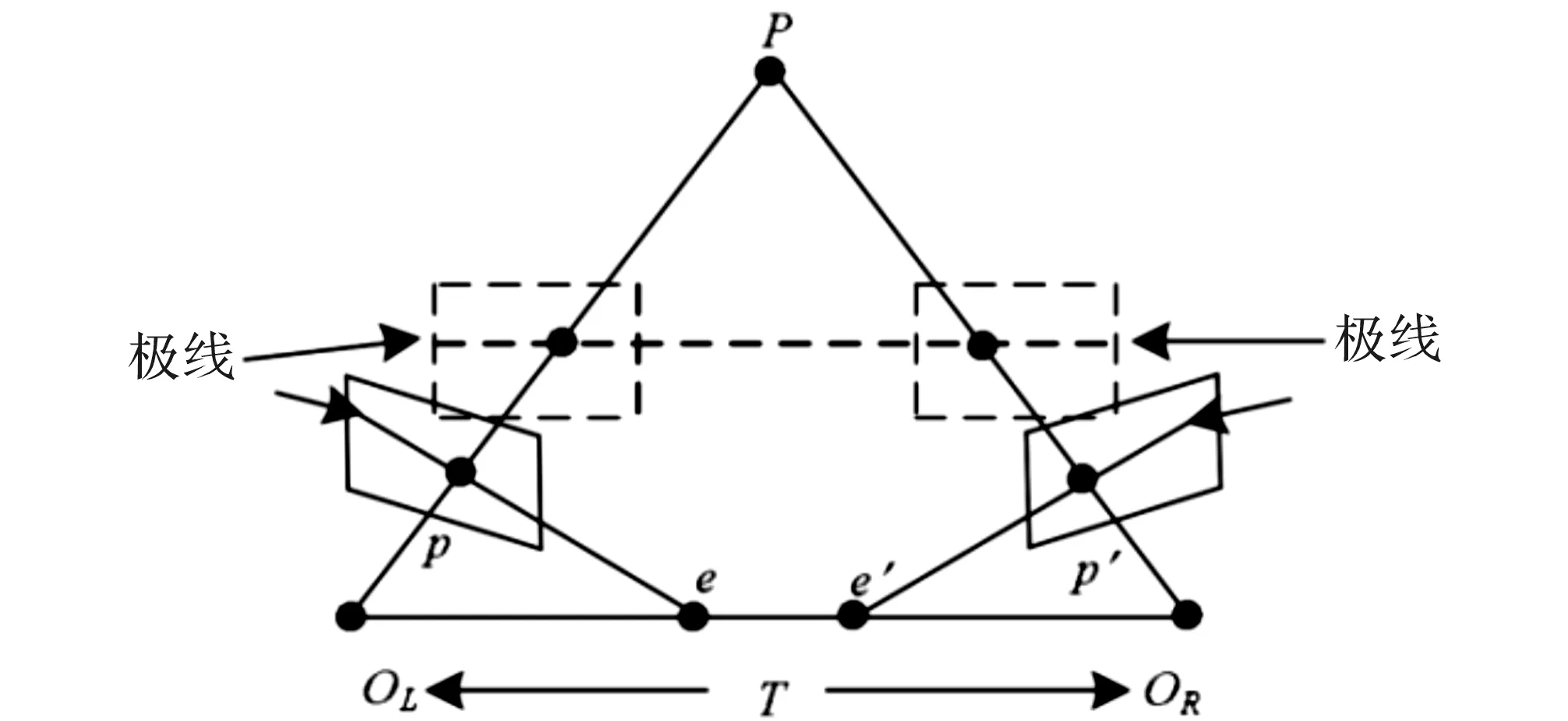
图1 立体视图极线几何(实线)和矫正后的极线几何(虚线)
2控制点变换矫正法的具体实现
2.1控制点变换法的实现原理
控制点变换对失真图像中所选定的一系列控制点的位移值来描述空间变换,这种方法的几何运算需要两个独立的算法。首先,需要通过控制点变换来定义空间变换本身,用其来描述每个像素如何从初始位置“移动”到终止位置,即每个像素的“运动”;同时,还需一个用于灰度级插值的算法,用来产生一个能保持连续性和连通性的光滑映射[6]。在文中的三维重构系统中,采集到的图像均先转换为灰度图进行处理,因此采用双线性插值法。这种方法的空间变换表达式为
u=Ax+By+Cxy+D
(3)
v=Ax+Bx+Cxy+D
(4)

图2 控制点的空间映射
如图2所示,四边形顶点直接映射到相应的矩形顶点上,而输入四边形内部的点则被映射到对应矩形内部的点上。
给定输入图像和输出图像相对应的 4 个控制点,便可得到 8 个线性方程,只要其中所有任意3个点均不在一条直线上,就可解出8个变换参数,其表达式如下
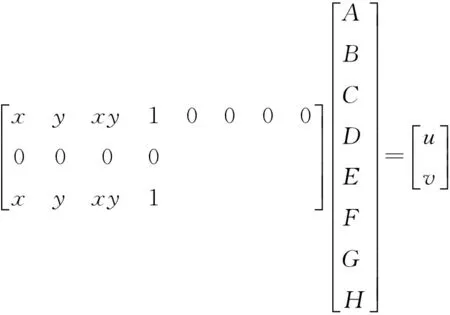
(5)
2.2控制点变换法的具体实现过程
2.2.1变换矩阵及变换系数的求取
假设输入图像为f(x,y),输出图像为g(u,v)。输入图像与输出图像的相应4个控制点坐标分别是,(x1,y1),(x2,y2),(x3,y3),(x4,y4)和(u1,v1),(u2,v2),(u3,v3),(u4,v4),则根据式(5),可得到输入图像与输出图像像素点之间的变换矩阵,如下所示
(6)
在式(6)中,控制点变换系数A~H和输入图像坐标(x1,y1),(x2,y2),(x3y3),(x4,y4)和输出图像控制点坐标(u1,v1),(u2,v2),(u3,v3),(u4,v4)的函数,因此式(5)可写成
u=u(x1,y1,x2,y2(x3,y3,x4,y4,u1,v1,u2,v2,
(u3,v3,u4,v4)))
(7)
v=v(x1,y1,x2,y2,(x3,y3,x4,y4,u1,v1,u2,v2
(u3,v3,u4,v4,x,y)))
(8)
2.2.2灰度插值算法的实现
实现赋值的方法有正向映射法和反向映射法,本文选择较容易实现的反向映射法。该方法是指从旋转图像上像素点坐标(x,y)出发,求出原始图像上对应的像素点坐标(x′,y′),然后将原始图像上对应像素点(x′,y′)的灰度值赋给旋转图像上对应像素点(x,y)[8],如图3所示。

图3 反向映射示意图
插值的方法有较多种,考虑到精度和运算速度,本文采用双线性插值法。双线性插值,又称为双线性内插,是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值,运算表达式为
g(u,v)=[f(x+1,y)-f(x,y)]x
+[f(x,y+1)-f(x,y)]y+f[(x+1,y+1)
+f(x,y)-f(x,y+1)-f(x+1,y)]xy+f(x,y)
(9)
由式(9)可看出,任意一点的灰度值由对应空间变换点相邻的4个像素灰度值共同决定。

图4 双线性插值算法解析图
如图4所示,已知A,B,C,D与待插值得到的点(x′,y′),为得到点(x′,y′),首先需要在x方向进行线性插值,得到E和F,然后再在y方向进行线性插值,即可得到点(x′,y′)。
假设(x′,y′)点的4个邻近像素A,B,C,D的坐标分别是(i,j),(i+1,j),(i,j+1),(i+1,j+1)。其灰度值分别为g(A),g(B),g(C),g(D)。首先计算E和F的灰度值g(E)和g(F)
g(E)=(x′-i)[g(B)-g(A)]+g(A)=
(i+1-x′)g(A)+(x′-i)g(B)
(10)
G(F)=(x′-i)[g(D)-g(C)]+g(C)=
(i+1-x′)g(C)+(x′-i)g(D)
(11)
再计算(x′,y′)点的灰度值,为
g(x′,y′)=(y′-j)[g(F)-g(E)]+g(E)=
(j+1-y′)g(E)+(y′-j)g(F)
(12)
线性插值的结果与插值的顺序无关。首先进行y方向的插值,然后进行x方向的插值,所得到的结果一致。但双线性插值插值方法并不是线性的,首先进行y方向的插值,然后进行x方向的插值,与首先进行x方向的插值,再进行y方向的插值,所得到的E与F是不同的。
3实验结论及分析

图5 三维重构系统中左右目图像极线矫正前与矫正后对比图
在三维重构系统中,采取双目摄像头外加辅助光栅的结构光图像采集模型。左右目相机在采集图像之后的原始图像如图5(a)和图5(b)所示,结合辅助线可看出,左右目摄像头拍摄到的图片明显不在同一水平线上,右边摄像头拍摄到的大象模型明显比左边高出较多。而经过极线矫正处理后,两个图像就被调整到了同一水平线上了,这样对后续匹配有较大帮助。

图6 右目图像极线矫正前后对比灰度图
以右图拍摄的图像为例,假设对其某一条水平线上,如图6所示的灰度值进行采样并将其用波形图显示,可得到如图7所示的波形图。
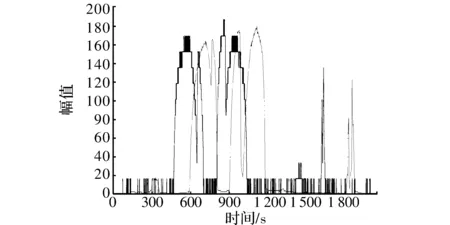
图7 右目图像极线矫正前后对比灰度值波形图
从灰度波形对比图来分析,矫正前和矫正后的波形大致相同,但明显可看出,矫正后的图像整体向左平移了150个像素点。此外,矫正前后的波形形状也有明显的差别,这是由于畸变造成的,因此矫正后与矫正前的大象模型在形状上也有差别。
4结束语
矫正后的波形较矫正前噪声略大,这是由于当对相邻4个像素点采用双线性插值时,所得表面在邻域处是吻合的,但斜率不吻合,且双线性灰度插值的平滑作用可能使得图像的细节产生退化,这种现象在进行图像放大时尤为明显。总体而言,文中的控制点变换法的极线矫正效果仍较为明显,这在后续的匹配中也得到了证实。
参考文献
[1]Andrea Fusiello,Emanuele Trucco,Alessandro Verri.A compact algorithm for rectification of stereo pairs[J].Machine Vision and Applications,2000(12):16-22.
[2]赖小波.机器人双目立体视觉若干关键理论问题及其技术实现研究[D].杭州:浙江大学,2010.
[3]蔡虹,叶水生,张永.一种基于模糊聚类的组合BP网络挖掘方法[J].计算机工程与应用,2005,41(36):83-85.
[4]王道累,杨峰.基于几何法立体图像校正的研究[J].图学学报,2014,35(6):883-888.
[5]李秀智,张广军.三目视觉图像的极线校正方法[J].光电工程,2007,34(10):50-54.
[6]关芳芳,程筱胜.基于极线校正的相移结构光三维测量[J].南京工程学院学报:自然科学版,2014,12(2):9-13.
[7]胡东红,汪浩,艾君,等.两种图像校正算法在实际应用中的比较[J].计算机工程与应用,2009,45(13):191-193.
[8]曹佃国,陈浩杰,李鹏.基于Matlab的双线性插值算法在图像旋转中的应用[J].中国印刷与包装研究,2010(4):74-78.
Algorithm for Rectification in 3-D Reconstruction System
TANG Bin, JIN Xuanhong
(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,
Shanghai 200093, China)
AbstractIn designing the 3-D reconstruction system, it is found that the accuracy and precision of 3D reconstruction results is subject directly to the accuracy of the rectification algorithm. The control point transformation is combined with the gray value interpolation algorithm to rectify the plume. This method defines the space transform itself by a control point transformation, which is used to describe how each pixel "mobile" from the initial position to the end position. Then, a smooth mapping is produced by grey value interpolation algorithm and the gray levels of pixels are changed to achieve rectification. Finally, the images before and after the rectification and their gray values are compared, showing that the whole image has a 150px left shift.
Keywordsrectification; control point transformation; bilinear interpolation
收稿日期:2015- 11- 10
作者简介:唐彬(1992-),女,硕士研究生。研究方向:测试计量技术及仪器。金晅宏(1978-),女,副教授,硕士生导师。研究方向:软件及机器视觉。
doi:10.16180/j.cnki.issn1007-7820.2016.07.004
中图分类号TP391.41
文献标识码A
文章编号1007-7820(2016)07-012-04

