基于MATLAB的强迫振动达芬方程的非线性幅频响应分析*③

陈赵江　陈 敏

(浙江师范大学数理与信息工程学院　浙江 金华　321004)



基于MATLAB的强迫振动达芬方程的非线性幅频响应分析*③

陈赵江陈 敏

(浙江师范大学数理与信息工程学院浙江 金华321004)

利用MATLAB研究了强迫振动达芬(Duffing)方程的非线性幅频响应特性，分析了达芬方程非线性幅频响应近似解析求解和数值求解的方法和步骤，给出了相应的MATLAB求解程序，并将解析解与数值解结果进行了比较.仿真程序和结果能够加深学生对非线性振动相关知识的理解，提高大学物理及相关力学课程的课堂教学效果.

达芬方程非线性振动非线性幅频响应跳跃现象MATLAB

强迫振动达芬方程(Duffingequation)在非线性振动领域是一个非常经典的实例，被广泛用来说明跳跃现象(Jumpingphenomena)、频响曲线弯曲和其他非线性行为.理解这个简单的低阶非线性方程的振动特性是学习更为复杂的非线性系统的基础.达芬方程解的跳跃现象与其非线性频响特性有直接的关系，因此对频响特性的研究非常重要.在目前大学物理以及相关力学课程的教学中，学生对非线性振动知识了解甚少，一知半解.如果能利用软件程序帮助学生了解掌握晦涩难懂的非线性振动知识，这将大大有益于相关教学工作的开展.目前已往文献对达芬方程非线性幅频响应的分析大多利用MAPLE和MATHEMATICA数学软件且缺少数值解和解析解的比较分析.本文给出了达芬方程非线性幅频响应近似解析求解和数值求解的方法和步骤，利用MATLAB的强大计算功能编写了相应的求解程序，并将解析解与数值解结果进行了比较分析，以满足学生对非线性振动知识的进一步理解.

1　达芬方程非线性幅频响应的理论分析

含阻尼和外部驱动力的无量纲达芬方程一般具有如下形式[1]

(1)

其中u是位移，t是时间，ζ是阻尼比，γ是立方刚度系数，F和Ω分别为激励幅值和激励频率.需注意的是，式(1)中所有物理量均为无量纲量，因此Ω其实是激励频率和系统固有频率之比,即

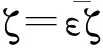
Ω=1+εσ

(2)

则式(1)可改写为

(3)

我们采用多尺度法[1]对上式进行近似解析求解，引入尺度T0=t和T1=εt

(4)

(5)

(6)

的式(3)的解.把式(4)～(6)代入式(3)，并令ε的同次幂的系数相等，我们得到

(7)

(8)

式(7)的通解可以表示为

(9)

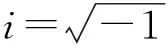
(10)

把A表示成如下的级数形式

(11)

则式(10)改写成

(12)

或

(13)

将式(13)分成实部和虚部，得出

(14)

(15)

式中a和β都是实数，引进变换

(16)

把式(14)和(15)化为自治系统，由式(16)

φ′=σ-β′

(17)

把式(16)代入式(14)和(15)，并利用式(17)可得

(18)

(19)

由于我们考虑稳态运动，即a和φ为常数值，设a′=0和φ′=0，可得到

(20)

(21)

对式(20)和(21)取平方，将结果相加，得出

(22)

通常称之为频率响应方程.利用式(2)我们将上式改写为Ω关于a的形式， 得到

(23)

从式(23)可知，对于某一幅值响应a，其对应两个激励频率Ω1,2，但这两个频率所对应的响应a可能是不稳定的.为了表征解的稳定性，考虑如下的动力学系统方程

(24)

其中，x1和x2为状态量.则上述系统的雅可比矩阵为

(25)

根据式(18)和式(19)，在本系统中状态向量分别为a和φ，f1和f2的表达式如下

(26)

因而可得系统的雅可比矩阵为

(27)

稳态运动的稳定性依赖于雅可比矩阵的特征值，式(27)所对应的特征方程如下

(28)

展开此行列式，可得

(29)

本系统的本征值如下

(30)

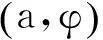
(31)

其中

2　达芬振动方程非线性幅频响应分析的MATLAB实现

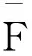
2.1MATLAB解析求解程序

从式(22)可以看出为了得到频率响应曲线，可解出a2关于σ的函数，或者可以解出σ关于a的函数.显然，后一种方法比较简单.因此，在编程时根据式(23)进行计算.以下为MATLAB求解程序：

%强迫振动达芬方程幅频响应曲线的解析求解

%参数设定

epsilon=0.2; %小参数

gamma1=4; %非线性参数

F1=0.5; %激励幅值

zeta1=0.25;%阻尼项

a=linspace(0.1,2.0,100); % 计算响应幅值范围

forii=1:1:length(a)

%根据(23)式，对应一个响应幅值，可能存在两个激励频率值；

%Omega1为较小的激励频率值

Omega1(ii)=(1+3*epsilon*gamma1/8*a(ii)^2-sqrt((epsilon*F1/(2*a(ii)))^2-(epsilon*

zeta1)^2));

%Omega1对应的本征函数值

lamOmega11=sqrt(-((Omega1(ii)-1)/epsilon-3*gamma1/8*a(ii)^2)*((Omega1(ii)-1)/epsilon-9*gamma1/8*a(ii)^2))-zeta1;

lamOmega12=-sqrt(-((Omega1(ii)-1)/epsilon-3*gamma1/8*a(ii)^2)*((Omega1(ii)-1)/epsilon-9*gamma1/8*a(ii)^2))-zeta1;

%Omega2为较大的激励频率值

Omega2(ii)=(1+3*epsilon*gamma1/

8*a(ii)^2+sqrt((epsilon*F1/(2*a(ii)))^2-

(epsilon*zeta1)^2));

%Omega2对应的本征函数值

lamOmega21=sqrt(-((Omega2(ii)-1)/epsilon-3*gamma1/8*a(ii)^2)*((Omega2(ii)-1)/epsilon-9*gamma1/8*a(ii)^2))-zeta1;

lamOmega22=-sqrt(-((Omega2(ii)-1)/epsilon-3*gamma1/8*a(ii)^2)*((Omega2(ii)-1)/epsilon-9*gamma1/8*a(ii)^2))-zeta1;

iflamOmega11==conj(lamOmega21)

%如果两个本征值相等退出计算(即此时计算到频响曲线最高点)

plot(Omega1(ii),a(ii),'k.','MarkerSize',15')

holdon

break

else

FG=((Omega1(ii)-1)/epsilon-3*gamma1/8*a(ii)^2)*((Omega1(ii)-1)/epsilon-9*

gamma1/8*a(ii)^2)+zeta1^2;% 对应上文中的(31)式

ifFG<0

plot(Omega1(ii),a(ii),'color',[.5 .5 .5],'MarkerSize',15) %不稳定点

else

plot(Omega1(ii),a(ii),'k.','MarkerSize',15)%稳定点

holdon

end

GF=((Omega2(ii)-1)/epsilon-3*gamma1/

8*a(ii)^2)*((Omega2(ii)-1)/epsilon-9*

gamma1/8*a(ii)^2)+zeta1^2;% 对应上文中的(31)式

ifGF<0

plot(Omega2(ii),a(ii),'.','color',[.5 .5 .5],'MarkerSize',15) %不稳定点

else

plot(Omega2(ii),a(ii),'k.','MarkerSize',15)%稳定点

holdon

end

xlabel('Omega') %x轴标题

ylabel('a')%y轴标题

xlim([0.5,1.5]); %x轴范围

ylim([0,2]);%y轴范围

end%满足条件退出循环(计算到幅频响应曲线顶点)

end%结束对不同a值的计算

2.2MATLAB数值求解程序

(32)

在MATLAB中定义如下函数并保存为duffing.m

functiondy=duffing(t,y)

globalepsilongamma1F1zeta1Omega

dy=zeros(2,1);

dy(1)=-zeta1*y(1)+F1/2*sin(y(2));

dy(2)=(Omega-1)/epsilon-3*gamma1/

8*y(1)^2+F1/(2*y(1))*cos(y(2));

end

(33)

在MATLAB中定义如下函数并保存为duffing1.m

functiondydt=duffing1(t,y)

globalepsilongamma1F1zeta1Omega

dydt=zeros(2,1);

dydt(1)=y(2);

dydt(2)=-2*epsilon*zeta1*y(2)-y(1)-epsilon*gamma1*y(1)^3+epsilon*F1*cos

(Omega*t);

end

达芬方程幅频响应数值求解主程序main.m如下：

clc

%closeall

clearall

globalepsilongamma1F1zeta1Omega样% 定义全局变量

%参数设定

epsilon=0.2; %小参数

gamma1 = 4; % 非线性参数

F1=0.5;%激励幅值

zeta1=0.25; %阻尼项

np=400;% 计算的频率数目

Omega1=linspace(.5,1.5,np); % 正向扫频时的频率

Omega2=linspace(1.5,.5,np); % 反向扫频时的频率

yy=[];

Y0=[0.1 0.1];% 初始值

fori=1:1:length(Omega1)

Omega=Omega1(i);

[T,Y] =ode45(@duffing,[0 400],Y0);

%[T,Y] =ode45(@duffing1,[0 400],Y0);

nn=length(Y(:,1));

ymax=max(Y(nn-round(nn/2):nn,1));% 取稳态幅值

ymax1=max(Y(nn-round(nn/2):nn,2));

Y0=[ymaxymax1];% 下一次计算的初始值

yy=[yy;ymax];% 保存计算结果到yy向量

end

plot(Omega1,yy,'k','LineWidth',1.5)% 正向扫频曲线用黑色表示

holdon

% 反向扫频

yy1=[];

ymax1=max(Y(nn-round(nn/2):nn,1));% 反向扫频的初始值

ymax2=max(Y(nn-round(nn/2):nn,2));% 反向扫频的初始值

forj=1:1:length(Omega2)

Omega=Omega2(j)

[T,Y1] =ode45(@duffing,[0 400],[ymax1ymax2]);

%[T,Y] =ode45(@duffing1,[0 400],Y0);

nn1=length(Y1(:,1));

ymax1=max(Y1(nn1-round(nn1/2):nn1,1));

ymax2=max(Y1(nn1-round(nn1/2):nn1,2));

yy1=[yy1;ymax1];

end

plot(Omega2,yy1,'color',[.5 .5 .5],

'LineWidth',1.5)% 反向扫频曲线用灰色表示

xlabel('Omega') %x轴标题

ylabel('a')%y轴标题

xlim([0.5,1.5]); %x轴范围

ylim([0,2]); %y轴范围

3　求解结果分析

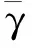
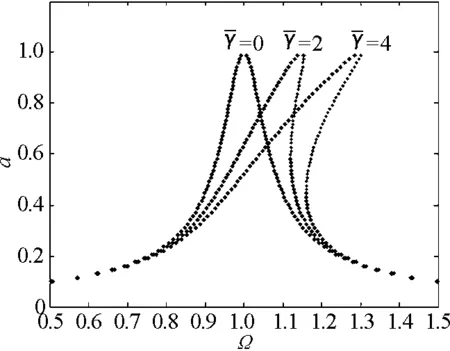
(a)随非线性参数的变化

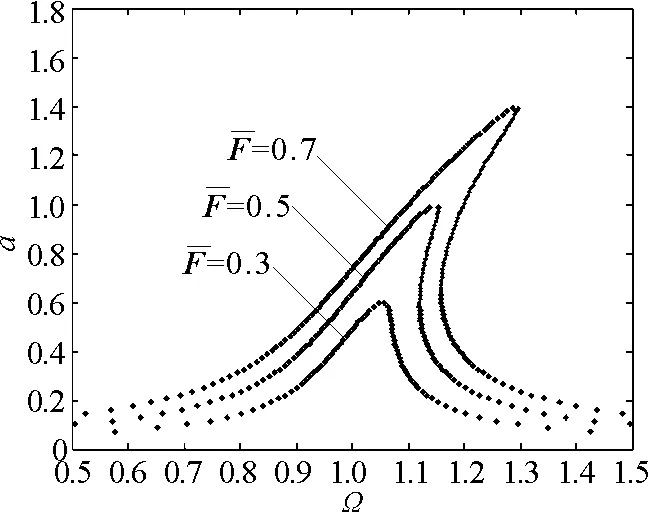
(b)随激励幅值的变化

其次，我们利用2.2节的幅频响应数值求解程序对强迫振动达芬方程的一阶近似幅频响应进行求解分析，其中使用的MATLAB子函数为duffing.m.图2中黑色和灰色曲线分别为正向和反向扫频计算结果.从图2可以发现当正向扫频(即频率比Ω增大)时，响应幅值一直增加.当进一步增加时，就发生从A点到B点的跳跃并伴随着响应幅值的突然减小.随后，响应幅值随Ω的增大而减小.对应着A点的最大振幅只有从较低的频率开始增加才可能达到.在另一方面，反向扫频(即频率比Ω减小)时，响应幅值也增加.当Ω进一步减小时就发生从C点到D点的跳跃并伴随着响应幅值的突然增加.随后，响应幅值随Ω的减小而减小.从图中也可发现解析解中的不稳定区域(从A点到C点)在数值求解时是无法得到的，幅频响应一阶近似解析解和一阶近似数值解结果符合很好.

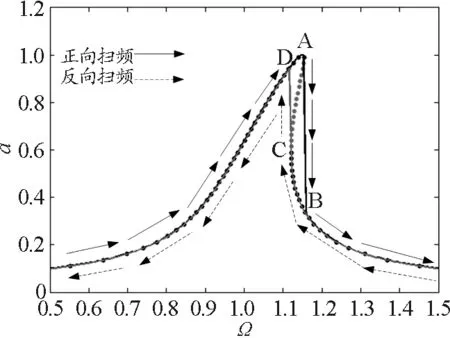
图2　强迫振动达芬方程的幅频响应数值与解析解的比较

最后，我们对强迫振动达芬方程的幅频响应做进一步的数值分析，其中使用的MATLAB子函数为duffing1.m.计算结果如图3所示，从图中可以发现数值解与近似解析解存在一定差异，且偏离Ω=1 越大两者的差别越大.这是因为这里数值求解的是最初的不包含近似的微分方程式(3)，而解析解是满足Ω≈1的一阶近似解.因此，当Ω越接近1时，两者解的结果越接近.从上述分析也可知近似解析解式(22)是在弱阻尼、弱非线性系数并接近共振时得出的结果，并不适用于所有的情况，这一点在学习的时候要特别注意.

图3　强迫振动达芬方程的幅频响应数值与解析解的比较

4　总结

本文对强迫振动达芬方程的非线性幅频响应特性进行了研究，分析了达芬方程非线性幅频响应解析求解和数值求解的方法和步骤，给出了相应的MATLAB求解程序，并将解析解与数值解结果进行了比较分析.仿真程序和结果能够加深学生对非线性振动的理解，提高大学物理以及相关力学课程的教学效果.此外，虽然本文只讨论了达芬方程的非线性幅频响应特性，但仿照本文的求解步骤和程序也容易对达芬方程的非线性相频特性进行分析.

1A·H·奈弗,D·T·穆克著. 非线性振动. 宋家骕, 罗惟德, 陈守吉译. 北京：高等教育出版社, 1980

2张志涌. 精通MATLABR2011a. 北京：北京航空航天大学出版社, 2011

陈赵江(1980-)，男，博士，主要从事大学物理教学和研究.

2016-03-08)

③浙江师范大学“十二五”省级实验教学示范中心重点建设项目和2015年度浙江师范大学教改项目资助.