Landau定理中上界的一个改进
郭辉,李文华
(深圳大学数学与统计学院,广东 深圳 518060)
Landau定理中上界的一个改进
郭辉,李文华
(深圳大学数学与统计学院,广东 深圳518060)
通过相关文献给出的穿孔平面C{0,1}的双曲度量的密度函数的新的下界估计,借助广义Schwarz引理我们对Landau定理中关于上界做了进一步改进并得到了一个带参数的上界表达式.并且当参数取到0时,此结论正好为相关文献得到的结果.
Landau定理;全纯函数;Poincar´e度量
1 引言
记∆={z:|z|<1}为单位圆,C{0,1}为穿孔平面,和ρ0,1(z)为穿孔平面双曲度量的密度函数.众所周知,Landau定理是复分析的一个重要的经典定理.设函数f(z)在单位圆∆内全纯,且不取0和1,并在原点有展式:f(z)=a0+a1z+a2z2+...,Landau定理断言:存在一个与f无关的常数C使得

(1.1)式中常数C被称为Landau常数.人们试图给出其最佳值.经过多年不断努力,最终在20世纪70年代末80年代初,先后由赖万才[1],Hempel[2]和Jenkins[3]彼此独立地给出了C的精确值:

其证明方法各有不同.
尽管如此,Landau定理的显式估计形式仍有改进的余地.1992年,李忠教授[4]在 Ahlfors[5],Hempel[2]及 Minda[6]等人的基础之上,给出了穿孔面 C{0,1}上双曲度量的密度函数ρ0,1(z)的新下界,并由此得到(1.1)式的一种改进形式,其结论(见文献[4]中定理1)如下:
定理 1.1设函数f(z)在单位圆∆内全纯,且不取0和1,并在原点有展式:

则存在一个绝对常数m>0使得下述估计式成立:
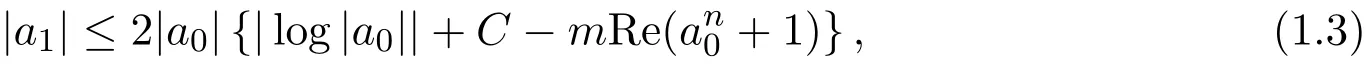
其中C是由(1.2)式决定的常数,而

(1.3)式中的等号当且仅当f是C{0,1}的全纯覆盖映射且a0=-1时成立.
本文通过李忠教授(见文献[4]中定理2)给出的穿孔平面C{0,1}的双曲度量的密度函数新的下界估计,借助广义Schwarz引理我们对定理A中关于(1.3)式做进一步改进,得到本文的主要结果如下:
定理 1.2设函数f(z)在单位圆∆内全纯,且不取0和1,并在原点有展式:
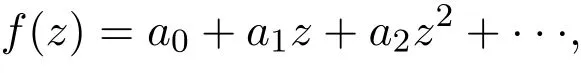
则存在一个绝对常数m>0使得下述估计式成立:

其中C是由(1.2)式决定的常数,α∈(0,0.01),且满足

式中β是一个由α按上式确定的常数,而n为(1.4)式中定义.(1.5)式中的等号当且仅当f 是C{0,1}的全纯覆盖映射且a0=-1时成立.
注1.1当定理1.1中α=0时,(1.5)式即为(1.1)式;而且从定理1.1的证明过程可知定理1.1对定理A中的上界估计做了改进.
2 定理 1.2的证明
首先,在证明定理1.1之前,我们介绍两个引理.
引理 2.1(广义Schwarz引理[7-8]) 设区域D与G,其Poincar´e度量分别为
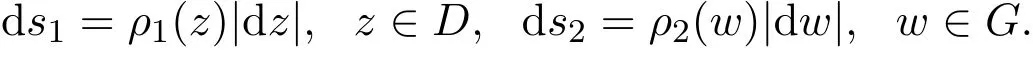
f:D→G为全纯函数,则

其中等号在一点成立的充要条件是f是D到G的全纯覆盖映射.
引理 2.2[4]设ρ0,1(z)|dz|为C{0,1}的双曲度量,其中Gauss曲率为-1.则
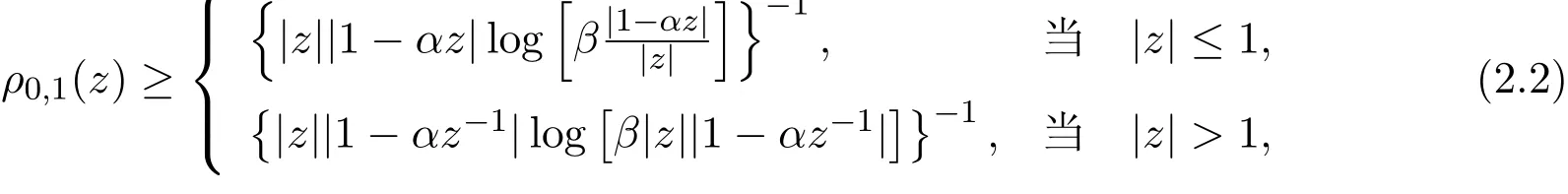
其中α和β与定理1.1中定义一样.且上式中取到等号当且仅当z=-1时成立.
定理 1.1的证明首先假设|a0|=|f(0)|≤1.由引理2.1得到

我们取z=0,(2.3)式变为ρ0,1(f(0))|f′(0)|≤2,即为

将(2.4)式代入引理2.2中(2.2)式第一个不等式,得到

令Q(ζ)=|1-αζ|log(β|1-αζ|/|ζ|)和R(ζ)=|log|ζ||+C,并假设T(ζ)=Q(ζ)-R(ζ),那么(2.5)式变为

比较(1.5)式,(2.5)式和(2.6)式的形式,知道要证明(1.5)式转化为估计T(a0).根据(1.6)式,得到

假定|ζ|≤1,那么有
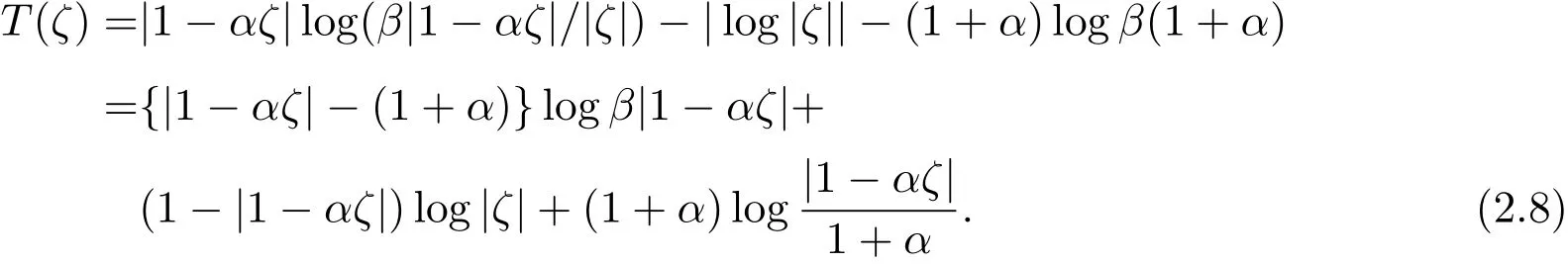
经过简单的计算知:

又因为|ζ|≤1,利用不等式(x-1)/x≤logx,(0<x≤1),得到

进而得到,
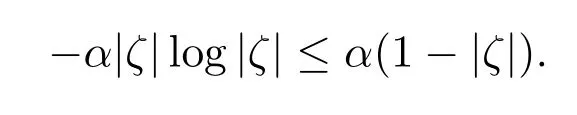
结合(2.9)式,得到:

又根据(2.9)式,可知

那么由(2.8)式,(2.10)式和(2.11)式,得到

令x=Reζ,y=Imζ,对|ζ|≤1,有

结合(2.12)式和(2.13)式,得到

因此当|a0|≤1时,令

令ζ=a0,根据(2.14)式,得到
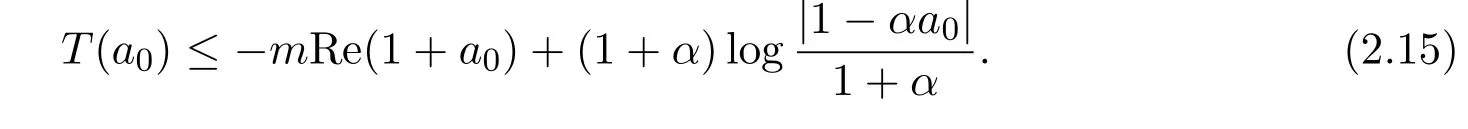
结合(2.6)式和(2.15)式,得到
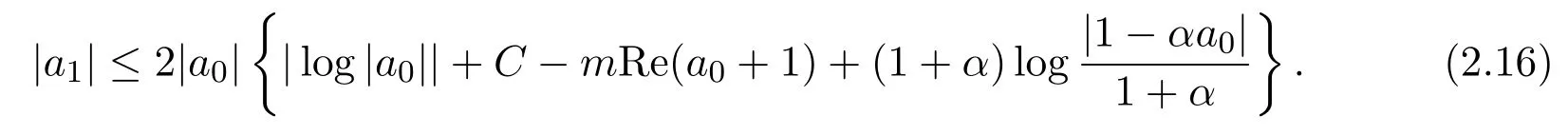
另一方面,当|a0|>1,将上述结果应用于F=1/f,同理可以得到,

取

那么结合 (2.16)式和 (2.17)式得到 (1.5)式.由证明过程中所应用的引理 2.1及引理 2.2 知(1.5)式中的等号当且仅当f是C{0,1}的全纯覆盖映射且a0=-1时成立.
[1]Lai W C.The precise value of Hayman’s constant in Landau’s theorem[J].Sci.in China,1978,5:495-500.
[2]Hempel J A.The Poincar´e metric on the twice punctured plane and the theorems of Landau and Schottky [J].J.London Math.Soc.,1979,20:435-445.
[3]Jenkins J A.On explicit bounds in Landau’s theorem II[J].Canad.J.Math.,1981,33:559-562.
[4]Li Z.A new explicit bound in Landau’s theorem[J].Sci.in China(Series A),1992,35:463-470.
[5]Ahlfors L V.Conformal Invariants:Topics in Geometric Function Theory[M].New York:McGraw-Hill Book Company,1973.
[6]Minda D.A reflection principle for the hyperbolic metric and applications to geometric function theory[J]. Complex Variables Theory Appl.,1987,8:129-144.
[7]李忠.复分析导引[M].北京:北京大学出版社,2004.
[8]李忠.拟共形映射与Teichm¨uller空间[M].北京:北京大学出版社,2013.
2010 MSC:30C20,30C35
A improvement of the upper bound in Landau theorem Guo Hui,Li Wenhua
(College of Mathematics and Statistics,Shenzhen University,Shenzhen 518060,China)
On the basis of the lower bound of the Poincar´e density of the twice-punctured plane C{0,1}which was given in related literature,we improve the upper bounder expression of Landau theorem and obtain a new upper bounder expression with a parameter by Schwarz Lemma.Moreover,the expression is the result in related literature when the parameter is zero.
Landau theorem,holomorphic function,Poincar´e metric
O174
A
1008-5513(2016)04-0337-05
10.3969/j.issn.1008-5513.2016.04.002
2016-04-28.
国家自然科学基金(11101290).
郭辉(1966-),博士,教授,研究方向:复分析.

