基于GPS/GLONASS星座卫星的星间GDOP最小值分析

肖 寅，姜兴龙，龚文斌，沈学民

（1．上海技术物理研究所 上海 200083；2．上海微系统与信息技术研究所 上海 200050；3．上海微小卫星工程中心 上海 201203）

基于GPS/GLONASS星座卫星的星间GDOP最小值分析

肖 寅1，3，姜兴龙2，3，龚文斌3，沈学民1，3

（1．上海技术物理研究所 上海 200083；2．上海微系统与信息技术研究所 上海 200050；3．上海微小卫星工程中心 上海 201203）

卫星自主定轨时选择测量卫星的几何构型对于定轨精度有着重要的影响，其影响程度由GDOP（几何衰减因子）来决定。GDOP值的下限限制了在一定的测量精度下的自主定轨精度。通过分别构建GPS星座和GLONASS星座并分析其构型特征，确定了接收机GDOP取理论最小值时的边界条件，利用均匀采样法分别得到GDOP的理论最小值，同时进一步用仿真数据验证了两者理论值的正确性。

自主导航；GDOP；均匀采样；卫星星座

GPS系统和GLONASS系统是目前全球四大卫星导航系统中发展历史最久，最具代表性的两个，同时两大系统理论上各自都可以构成星间链路，通过星间双向测距以达到卫星在长时间得不到地面系统支持的情况下自主导航的功能。

在星间双向测距中选择哪些导航卫星作为测量对象是建立星间链路的关键技术之一，其中一个重要的选择指标就是GDOP值的大小。这是因为GDOP代表从测量误差的标准差到用户接收机位置解的放大量。如果选择的卫星使这个值较小，那么测量误差的放大量就小，从而使导航卫星的定位比较精确。因此，找到GDOP的最小值以及接近这个值的卫星几何构型对于在自主导航的情况下提高导航卫星自身的定轨精度具有重要的意义。

不同的星座构型限制了导航卫星可以选择星间测量的卫星范围，从而使其能够达到的GDOP值范围也不同。文中首先通过STK仿真软件构建了GPS/GLONASS导航星座系统，分别确定了两大导航星座中任意两颗可见卫星的俯仰角范围，即计算理论GDOP最小值的边界范围；然后将其引入到地面接收机GDOP的计算公式，进而得到星载接收机理论GDOP最小值的计算方法及边界条件，并用均匀采样法得到在四颗卫星情况下两大系统GDOP值的理论下限；最后通过仿真得到的轨道数据计算出GDOP最小值，验证了理论最小值的正确性。

1　建立GPS/GLONASS仿真模型

STK的全称是Satellite Tool Kit（卫星软件工具包），是由美国AGI公司开发的一款在航天工业领域应用的商业化分析软件。它作为一种可以方便快捷地分析复杂的陆、海、空、天、电（磁）任务的专业仿真平台，能够提供简单易懂的图表和文本形式的分析结果，来确定最优方案［1］。

在STK中设置表1中的卫星轨道参数，构成GPS和GLONASS两个导航系统的Walker星座。

仿真建立的GPS星座和GLONASS星座的平面图如图1所示。

表1　GPS/GLONASS轨道参数Tab.1　Orbit parameters of GPS/GLONASS

根据STK产生的轨道坐标分别确定GPS/GLONASS系统每两颗卫星的俯仰角范围。GLONASS星座的星间俯仰角范围为0．679°～75．527°；GPS星座的星间俯仰角范围为10．381° ～76．112°。

2　GDOP的定义

GDOP是几何因子，它代表从测量误差的标准差到解的放大量，其值仅仅是卫星/用户几何布局的函数。对j颗卫星进行伪距测量，得到伪距测量误差与位置误差的关系［2］，写成矩阵形式为：

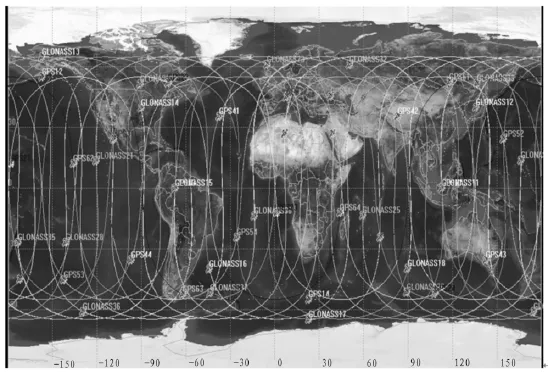
图1　GPS/GLONASS星座分布Fig．1　The satellite constellation distribution of GPS/GLONASS

其中axj，ayj和azj各项表示接收机近似位置指向第j颗卫星的单位矢量的方向余弦。

其最小二乘解为 Δx=（HTH）-1HTΔ ρ，其协方差阵为，得到

其中

3　GDOP最小值计算分析

导航卫星的接收机与地面接收机在选星方案中有相似之处，也有区别之处。相似之处在于，地面接收机可以到卫星信号的俯仰角不能小于0°，这是因为接收机位于地球球面之上，低于0°的卫星是不可见的。导航卫星可以接收到其他导航卫星信号的俯仰角也不能小于0°，这是因为导航卫星都是分别处于一个半径（这个半径就是卫星的轨道高度加上地球的半径）相同球面之上，我们沿着其中一颗卫星的质点做这个球面的切面，就会发现所有的导航卫星都处于这个切面一侧，另一侧无导航卫星。不同之处在于收到星座构型的影响和地球遮挡的原因，星间俯仰角范围受到了进一步的限制。

下面根据文献［5］的方案对H矩阵进行分块，令HTH=

当n=4时，可构造如下解：

这一组解的几何意义是接收机与被测量卫星构成一个六面锥，接收机位于锥顶位置。接收机与其中两颗被测量卫星构成的平面正交于这个接收机与另外两个被测量卫星构成的平面。式子中的α，β角分别是接收机指向被测量卫星的连线与Z轴（指向地心）的夹角，即π/2-θ（θ为接收机本体坐标系中其他被测量卫星的俯仰角）。

将上式代入到GDOP公式中，可以得到

4　GDOP最小值解算验证

对于GPS星座，通过仿真得到每两颗卫星之间的俯仰角最小值范围为10．4°至76．1°，由此可得10．4°＜α，β＜76．1°。则

对于该二元函数的条件极值问题，本文采用均匀采样方法，将（8）式中的α，β划分为的64×64的网格，在网格中步进为1°均匀采样后计算，得到GDOPmin=1．915。结果如图2所示。

同理可知对于GLONASS星座，其边界条件为14．5°＜α，β＜89．3°，α≠β，计算得GDOPmin=1．724，如图3所示。

下面根据STK生成的卫星在24小时内的星历求出H矩阵数值，通过公式（6）分别计算两个星座系统每300 s步进条件下任意4颗卫星与初始卫星的GDOP的最小值。GPS星座的仿真最小值为2．464，而GLONASS星座的仿真最小值为2．225，如图4所示。

图2　GPS星座星间GDOP理论最小值Fig．2　The theoretical minimum value of GDOP for GPS

图3　GLONASS星座星间GDOP理论最小值Fig．3　The theoretical minimum value of GDOP for GLONASS

图4　建模仿真计算GDOP最小值Fig．4　The simulation minimum value of GDOP for GPS/GLONASS

通过图4我们可以看到，由于受到轨道面和卫星相位差的原因，GPS和GLONASS仿真得到的GDOP最小值都是小于理论最小值的，并且GPS仿真最小值大于GLONASS仿真最小值，这也与二者的理论最小值关系保持了一致。

5　结束语

本文构建了 GPS/GLONASS卫星星座模型，对星间GDOP最小值进行了分析和推导，当接收机在n颗卫星的空间几何分布满足一定条件时，GDOP达到最小值，得到了4颗卫星链路条件下GDOP理论公式。得出了两个星座GDOP最小值计算的边界条件，并利用均匀采样法求得了此值。最后通过生成的星历数据遍历整个星座求得该星座的GDOP仿真最小值，验证了限定边界条件下的理论最小值的正确性。

［1］高晋宁，方源敏．基于STK的GLONASS系统与GPS系统DOP值的仿真分析［J］．科学技术与工程，2011，11（15）:3384．

［2］Elliott D Kaplan，Christopher J，Hegarty．Understanding GPS: principles and applications［M］．Artech House Inc．2006．

［3］Yarlagadda Ali，ADhahirN．GPS GDOP Metric［J］．IEE Proceeding，Radar，SonarNavigation，2000，147（5）: 2592264．

［4］盛琥，杨景曙，曾芳玲．伪距定位中的GDOP最小值［J］．火力与指挥控制，2009，34（5）:22-24．

［5］陈坡，韩松辉．卫星导航中GDOP最小值的分析与仿真［J］．弹箭与制导学报，2013，34（5）:1-5．

［6］丛丽，Ahmed I Abidat，谈展中．卫星导航几何因子的分析与仿真［J］．电子学报，2006，34（12）:2204-2208．

［7］丛丽，谈展中．提高卫星导航定位精度和实时性的选星算法［J］．系统工程与电子技术，2008，30（10）:1914-1917．

［8］YANG Yong，MIAO Ling-juan．GDOP results in all-in-view positioning and in four optimum satellites positioning with GPS PRN codes ranging［C］//IEEE Position Location and Navigation Symposium，2004:723-727．

［9］WU Chih-Hung，HO Va-Wei．Genetic Programming for the Approximation of GPS GDOP［C］//Proceedings of the Ninth InternationalConferenceonMachineLearningand Cybernetics，Qingdao，2010．

［10］Sairo H，Akopian D，Takala J．Weighted dilution of precision as quality measure in satellite positioning［J］．IEE Proc．-Radar Sonar Navig．，2003，150（6）:430-436．

Analysis of GDOP minimum value for autonomous navigation based on GPS/GLONASS constellation

XIAO Yin1，2，JIANG Xing-long2，3，GONG Wen-bin3，SHEN Xue-min1，3
（1．The Shanghai Institute of Technical Physics，Shanghai 200083，China；2．Shanghai Institute of Microsystem and Information Technology，Shanghai 200050，China；3．Shanghai Engineering Center for Microsatellites Shanghai 201203，China）

Geometry of measuring satellites has important implications for precision of the autonomous orbit determination．Currently，the affecting of the geometry for terrestrial receiver and a navigation satellites on the positioning precision is mainly measured by the GDOP．The lower limit of GDOP limits the measurement accuracy of a positioning accuracy range of the user．Constructing navigation constellation of GPS and GLONASS determines the boundaries for taking the minimum value of GDOP of the terrestrial receiver．Using uniform sampling get the minimum GDOP．Simultaneously，the simulation data verified the correctness of the minimum GDOP．

autonomous navigation；GDOP；uniform sampling；satellite constellation

TN961

A

1674－6236（2016）02-0021-04

2015-03-13稿件编号：201503191

肖 寅（1986—），男，湖北武汉人，博士研究生。研究方向：导航卫星自主导航技术。