实对称矩阵对角化中正交矩阵的初等变换求法

陈　亮，　杜翠真，　高　勤

(1.淮北师范大学数学科学学院，安徽淮北235000；2.淮北师范大学信息学院数学系2011级数学与应用数学，安徽淮北235000)



实对称矩阵对角化中正交矩阵的初等变换求法

陈亮1，杜翠真1，高勤2

(1.淮北师范大学数学科学学院，安徽淮北235000；2.淮北师范大学信息学院数学系2011级数学与应用数学，安徽淮北235000)

对实对称矩阵正交对角化过程中正交矩阵的求解方法进行了研究，给出了利用初等变换求解正交矩阵的方法，该方法不需要通过特征方程求解特征值与特征向量，仅仅使用初等变换和Schmidt正交化方法.

对称矩阵； 对角化； 正交变换； 初等变换

1　引　　言

实对称矩阵是一类应用广泛的矩阵，很多科学问题的求解都离不开实对称矩阵.而实对称矩阵的正交对角化问题，是个非常重要的问题，因为正交对角化具有很多优越的性质.比如正交变换不改变向量的范数，这个性质在物理学中有很大用处，物理学中的坐标系变换都使用正交变换，相对论中的变换也参考了正交变换的形式.再比如，正交对角化的计算量较小，变换矩阵很容易得到等.

对于实对称矩阵的正交对角化的求解，一般采取的方法是先求解出n阶实对称矩阵A的特征值，然后根据特征值，利用Schmidt正交化方法求出n个标准正交向量，从而得到实对称矩阵A的对角形，并得到所使用的正交变换[1-2].另外很多文献[3-7]也对实对称矩阵的正交对角化方法做了大量的介绍.本文介绍了一种利用初等变换求解实对称矩阵对角化中正交矩阵的方法，在初等变换的过程中，不需要通过特征方程求解特征值与特征向量，只利用我们熟知的初等变换和Schmidt正交化方法即可得到正交变换.

2　理论依据

为了叙述方便，假定本文进行的探讨均在实数域内.

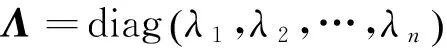
引理2[1]矩阵A可逆的充分必要条件是它能表示成一系列初等矩阵的乘积.

由于正交矩阵T是可逆的，且其逆矩阵T-1=T′也为正交矩阵，所以对于实对称矩阵A，存在一系列初等矩阵P1,P2,…,Pm，使得

T=P1P2…Pm，

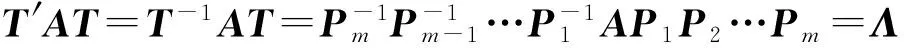
(1)

注意到，初等矩阵的逆矩阵仍然是初等矩阵[2]，且

P(i,j)-1=P(i,j)，P(i(k))-1=P(i(k-1))，P(i,j(k))-1=P(i,j(-k))

上面的讨论提示了一种将对称矩阵对角化的方法.设A为一n阶实对称矩阵，存在一系列初等矩阵，使得

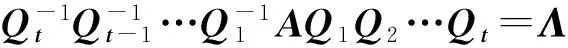
(2)

记B=Q1Q2…Qt，则B可表示为

B=EnQ1Q2…Qt.

(3)

由(2)，(3)知，如果用一系列初等列变换和相应的逆初等行变换把对称矩阵A对角化，那么对单位阵En实行同样的初等列变换，就可以得到变换矩阵B.即

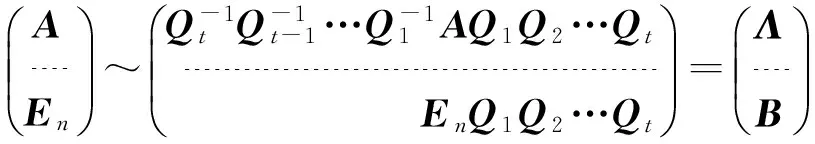
(4)

为了得到正交矩阵(变换)T，需要利用Schmidt正交化方法，将变换矩阵B化为正交矩阵T.由于实对称矩阵存在重根的情形，且属于不同特征值的特征向量正交，因此，这里我们只讨论存在一个n-1重特征值的情形，其余情形可以类推得到.

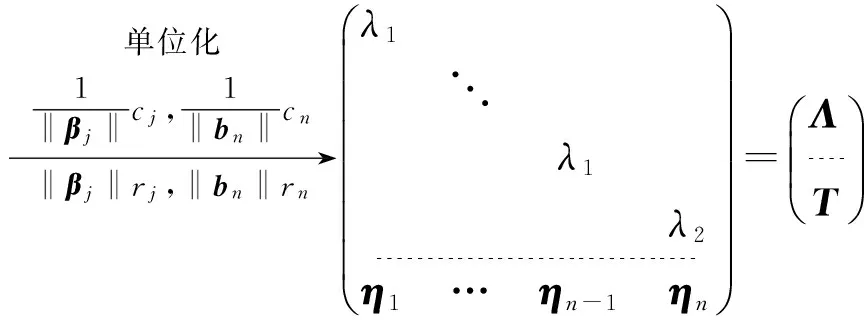
在使用Schmidt正交化方法的过程中，仍然是对矩阵进行初等变换.

综合以上情形，得到利用初等变换法求解实对称矩阵对角化中正交矩阵的方法

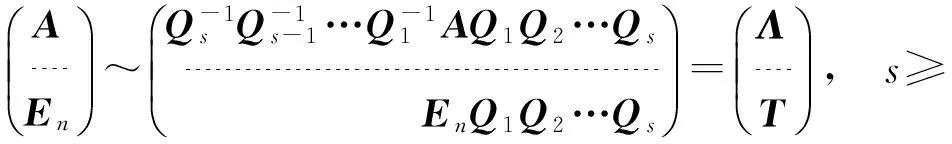
(5)

同理，也可得到初等行变换求对角化中正交矩阵的方法

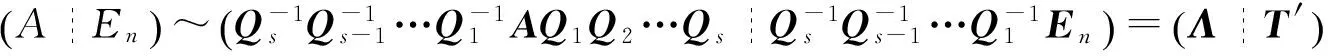
(6)

需要注意的是，(5)式在对变换矩阵正交化时，只能对下端矩阵的列向量进行Schmidt正交化，而(6)式中，只能对右端变换矩阵的行向量进行Schmidt正交化.

3　例　　题

下面利用初等变换法求解实对称矩阵对角化中的正交矩阵.

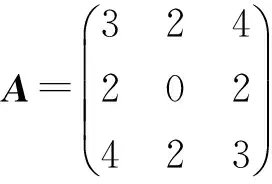
解法一利用初等列变换(5)式求解对角化中的正交矩阵，这里采取先进行初等列变换，再进行相应的逆初等行变换的顺序.由

解法二利用初等行变换(6)式求解对角化中的正交矩阵，这里我们采取先进行初等行变换，再进行相应的逆初等列变换的顺序.由

解法三利用初等行变换(6)式求解对角化中的正交矩阵，此时采取先进行初等列变换，再进行相应的逆初等行变换的顺序.由

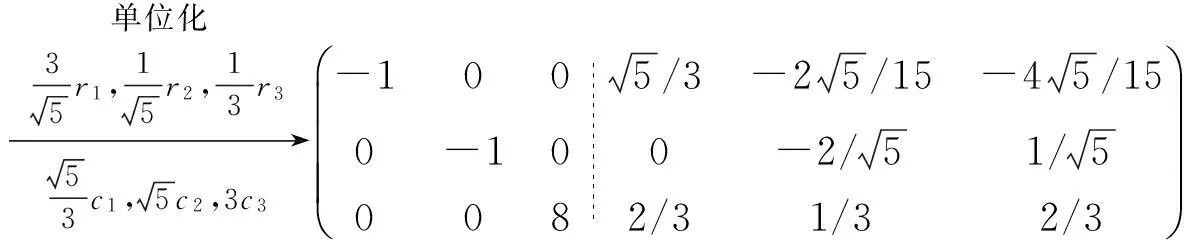
注由于法一与法二求解顺序及初等变换的过程相同，所以得到的正交矩阵也相同，而法三采取了与法二不同的求解顺序，所以得到了与法二不同的正交矩阵.从而说明，当采用了不同的初等变换顺序时，可能会得到不同的正交矩阵，这在理论上仍然是成立的.

4　结　　论

通过例题可以看出，对称矩阵正交对角化的初等变换法，规避了常规对角化过程中求解特征多项式和多次求解线性方程组的过程，只利用我们熟知的初等变换和Schmidt正交化方法即可得到正交变换.

说明本文的思路源于毕业论文的指导过程，感谢张云副教授参与讨论.

[1]北京大学数学系几何与代数教研室前代数小组，王萼芳，石生明，修订.高等代数 [M].3版.北京：高等教育出版社，2003.

[2]同济大学数学系.工程数学线性代数 [M].5版.北京：高等教育出版社，2012.

[3]雷英果.相似变换阵与合同变换阵的初等变换求法[J].大学数学，2001，17(2)：77-80.

[4]黎前修.用矩阵初等变换将矩阵对角化的方法[J].渝西学院学报，2002，15(1)：40-44.

[5]张立卓.关于矩阵对角化的探讨[J].大学数学，2014，30(6)：74-78.

[6]付立志，杨庆玺.对称矩阵对角化的正交变换模型[J].河南科学，2008，26(2)：135-137.

[7]刘学鹏.特殊矩阵的特殊对角化方法研究[J].大学数学，2005，21(5)：112-115.

An Elementary Transformation Method for Orthogonal Matrix in Solving Diagonalization of Real Symmetric Matrices

CHEN Liang1,DU Cui-zhen1,GAO Qin2

(1. School of Mathematical Science, Huaibei Normal University, Huaibei Anhui 23500, China；2. Grade 2011, Major in Mathematics and Applied Mathematics, Department of Mathematics, Information College,Huaibei Normal University, Huaibei Anhui 23500,China)

A method by using elementary transformation for orthogonal matrix in diagonalizing real symmetric matrices is mainly introduced in this paper, which does not require eigenvalue and eigenvector by solving characteristic equation, only using elementary transformation and Schmidt orthogonalization.

symmetric matrix; diagonalization; orthogonal transformation; elementary transformation

2015-07-23；[修改日期]2016-04-01

国家自然科学基金项目(61300048)；安徽省自然科学基金项目(1308085QF117，1508085MA14)；安徽省高校省级自然科学研究重点项目(KJ2014A223)；2014年安徽省高校优秀青年人才支持计划；安徽省高等教育振兴计划重大教学改革研究项目(2014ZDJY058)；安徽省教育厅质量工程项目(2012GXK058)；淮北师范大学教学研究项目(JY13231,JY14148)

陈亮(1977-)，男，博士，副教授，从事数值计算研究.Email:clmyf2@163.com

O151

C

1672-1454(2016)04-0068-05