线性方程组的4种迭代方法

雍龙泉

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)



线性方程组的4种迭代方法

雍龙泉

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

研究了线性方程组的4种迭代方法——Jacobi迭代、Gauss-Seidel迭代、HSS迭代、Richardson迭代，给出了4种迭代方法收敛的充分条件。数值实验进一步表明，在大规模线性方程求解时，迭代矩阵谱半径的大小决定算法的收敛速度；在谱半径小于1的前提下，谱半径越小，则收敛速度越快。

线性方程组；Jacobi迭代；Gauss-Seidel迭代；HSS迭代；Richardson迭代；谱半径

考虑如下线性方程组

记

当矩阵A∈Rn×n非奇异时，方程组Ax=b具有唯一解。

消去法是求解线性方程组的一类有效方法，但是针对大规模线性方程组，消去法计算效率较低，而迭代法能够快速地收敛到线性方程组的解[1]。迭代法的基本思想就是构造方程组Ax=b的等价方程组x=Bx+f，从而建立迭代公式

当迭代矩阵B的谱半径ρ(B)<1时，则对任意的初始向量x0∈Rn，迭代法都收敛[2-4]。

在构造线性方程组的迭代时需要注意两个原则：

①迭代矩阵谱半径要小于1，即首先要保证收敛；

②迭代矩阵谱半径远小于1，则迭代收敛越快。

下面给出4种常见的迭代方法。

1　迭代方法及收敛性

1.1Jacobi迭代

考虑线性方程组Ax=b，这里A∈Rn×n，记

假设aii≠0，i=1,2,…,n。则Jacobi迭代为

(1)

其中BJ=-D-1(L+U)， fJ=D-1b。

1.2Gauss-Seidel迭代

利用Jacobi迭代，可得Gauss-Seidel迭代为

(2)

其中BS=-(L+D)-1U， fS=(L+D)-1b。det(L+D)=a11a22…ann≠0，故(L+D)-1存在。

下面给出Jacobi迭代与Gauss-Seidel迭代收敛的充分条件。

定理1(1)若矩阵A∈Rn×n是严格对角占优，则Jacobi迭代与Gauss-Seidel迭代均收敛；(2)若矩阵A∈Rn×n是对称正定矩阵，则Gauss-Seidel迭代收敛，Jacobi迭代不一定收敛。

定理1的证明见文献[1,5]。

1.3HSS迭代

考虑线性方程组Ax=b，这里A∈Rn×n，且A为广义正定矩阵。对矩阵A做分解A=H+S，其中H=(A+AT)/2，S=(A-AT)/2，H称为A的对称分量，S称为A的反对称分量；显然，n阶实方阵A的对称分量H和反对称分量S是唯一的。A是广义正定矩阵的充分必要条件是A的对称分量H是对称正定矩阵[6-7]。

A是广义正定矩阵，则A的对称分量H是对称正定矩阵。记矩阵H的特征值为0<λmin=λ1≤λ2≤λ3≤…≤λn-1≤λn=λmax，对任意的α>0，构造方程组Ax=b的迭代格式为

(3)

这里B(α)=(αI+S)-1(αI-H)(αI+H)-1(αI-S)，G(α)=2α(αI+S)-1(αI+H)-1，称迭代(3)为线性方程组Ax=b的HSS迭代[8]。下面给出HSS迭代法的收敛性。

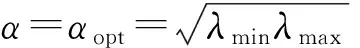
定理2的证明见文献[8-9]。

当A是对称正定矩阵时，H=A，S=O，此时

1.4Richardson迭代

考虑线性方程组Ax=b，这里A∈Rn×n，且A为对称正定矩阵，设矩阵A的特征值为0<λmin=λ1≤λ2≤λ3≤…≤λn-1≤λn=λmax，对任意的τ>0，方程组Ax=b等价于x=(I-τA)x+τb，构造迭代

(4)

这里B(τ)=(I-τA)，称迭代(4)为线性方程组Ax=b的Richardson迭代[10]。下面给出Richardson迭代法的收敛性。

定理3的证明见文献[11]。

定理1、定理2、定理3分别给出了Jacobi迭代、Gauss-Seidel迭代、HSS迭代、Richardson迭代收敛的充分条件，这4种迭代都有严格的适用范围；对一般矩阵，若不满足上述条件，则只能用迭代矩阵的谱半径来判别收敛性；理论上，在谱半径小于1的前提下，谱半径越小，则收敛速度越快。下面通过算例来说明上述4种迭代法的收敛性。

2　数值实验

算例考虑线性方程组Ax=b，其中

方程组的精确解为x=(1,1,…,1)T∈Rn。这里矩阵A严格对角占优，且为广义正定矩阵(由于其对称分量H是对称正定矩阵，故A是广义正定矩阵)，因此，该线性方程组可以用Jacobi迭代、Gauss-Seidel迭代、HSS迭代进行求解；由于矩阵A不是对称正定，因此不能直接用定理3来判别Richardson迭代的收敛性，只能用谱半径来判别迭代是否收敛。

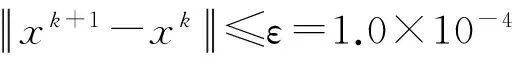
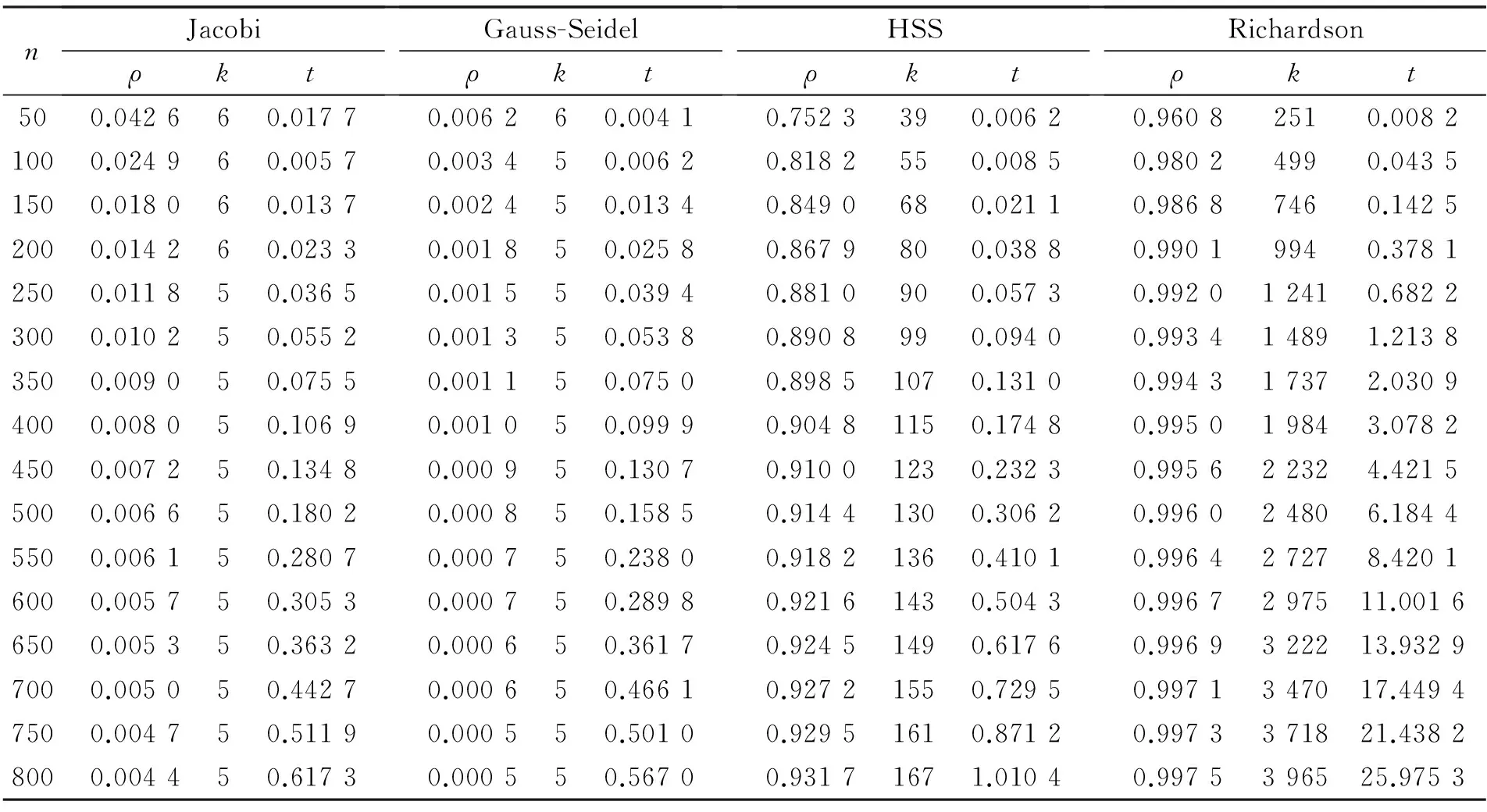
表1　4种迭代法的计算结果

注：ρ表示迭代矩阵谱半径，k表示迭代次数，t表示运行时间(单位：s)。

文献[12-13]表明，针对大规模线性方程组，HSS迭代法适用范围广，且计算效率高。但是对该问题而言：(ⅰ)随着维数的增加，4种迭代矩阵谱半径都小于1，因此上述4种迭代都收敛；(ⅱ)随着维数的增加，Jacobi和Gauss-Seidel迭代的谱半径却在减小(图1)，因此迭代次数和运行时间较少；而HSS和Richardson迭代的谱半径在增大(图2)，因此迭代次数和运行时间变大；(ⅲ)随着维数的增加，Jacobi和Gauss-Seidel迭代谱半径都远远小于1，且Gauss-Seidel的谱半径更小，因此Gauss-Seidel收敛速度更快，精度更高。图1、图2分别给出了在不同维数下迭代矩阵的谱半径。

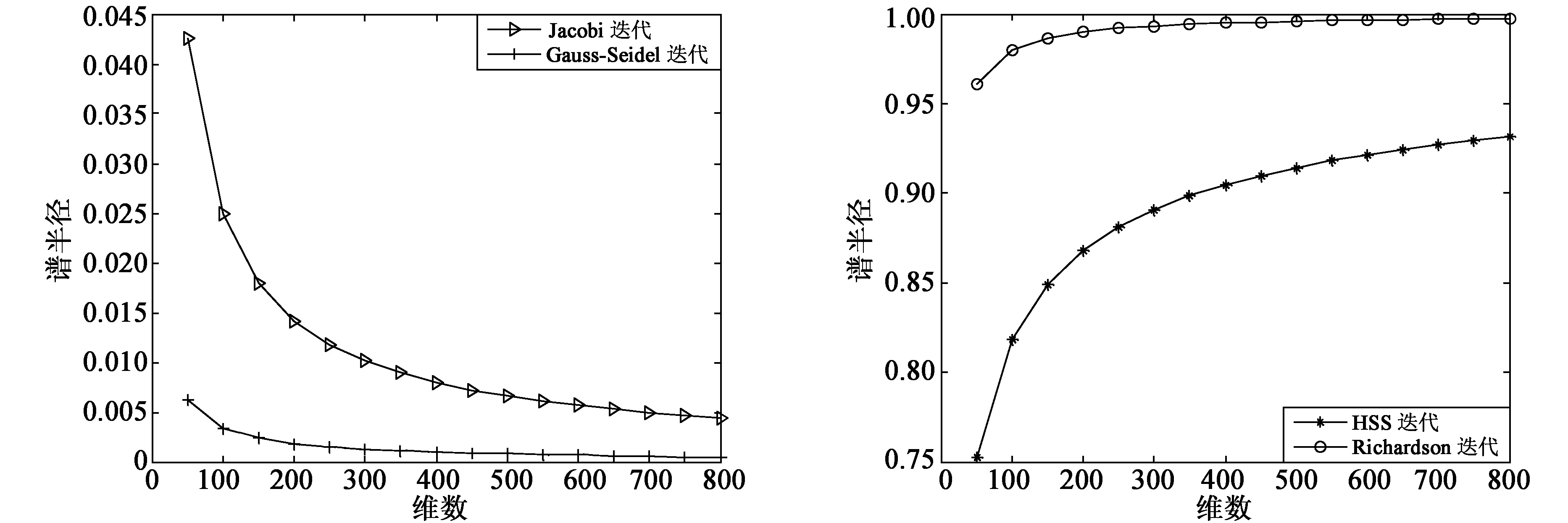
图1　Jacobi与Gauss-Seidel迭代谱半径　　　　　图2　HSS与Richardson迭代谱半径

该例子进一步表明，在大规模线性方程求解时，若选用迭代算法，一定要重点考察迭代矩阵的谱半径，在谱半径小于1的前提下，谱半径越小，则收敛速度越快。

图3—图6分别给出了n=50时Jacobi迭代、Gauss-Seidel迭代、HSS迭代、Richardson迭代的收敛过程(横轴表示迭代次数，纵轴表示迭代过程中向量x分量的取值)。

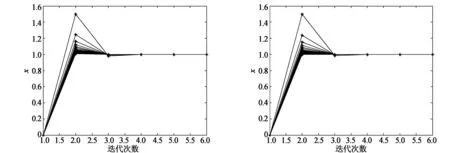
图3　Jacobi迭代的收敛过程　　　　　　　　　图4　Gauss-Seidel迭代的收敛过程

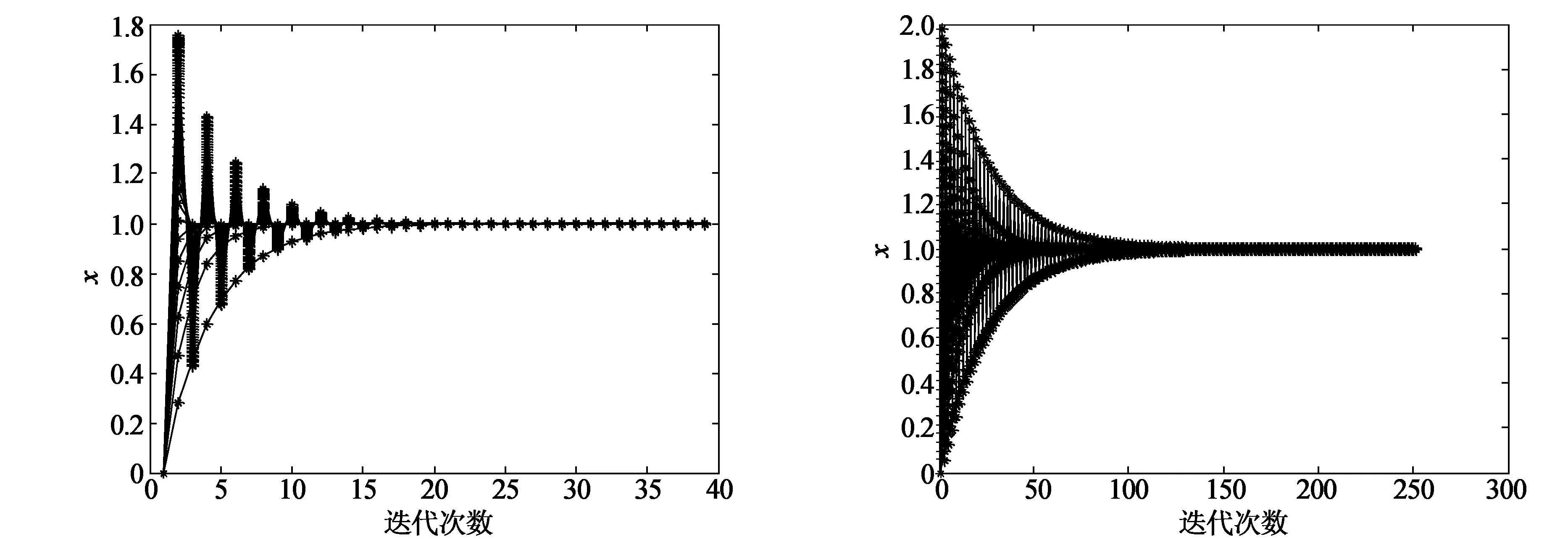
图5　HSS迭代的收敛过程　　　　　　　　　图6　Richardson迭代的收敛过程

限于篇幅，其余维数的收敛过程图不一一列出；针对该问题而言，随着维数的增加，HSS迭代和Richardson迭代的谱半径接近1，收敛呈现振荡性，因此收敛较慢；而Jacobi迭代和Gauss-Seidel迭代的谱半径远远小于1，因此收敛速度较快。

3　结　语

本文研究了线性方程组常见的4种迭代方法，给出了4种迭代方法收敛的充分条件。对一般矩阵，若不满足这些充分条件，则只能用迭代矩阵的谱半径来判别收敛性；因此，在实际问题求解时，如果能够找到多种收敛的迭代方法，则需要重点比较迭代矩阵的谱半径，在谱半径小于1的前提下，谱半径越小，则收敛速度越快。

[1]谷同祥,安恒斌,刘兴平,等.迭代方法和预处理技术:上册[M].北京:科学出版社,2015:21-186.

[2]徐树方,高立,张平文.数值线性代数[M].2版.北京:北京大学出版社,2013:15-197.

[3]王转德.迭代矩阵的谱分析[D].成都:电子科技大学,2009.

[4]李爱芹.线性方程组的迭代解法[J].科学技术与工程,2007,7(14):3357-3364.

[5]杨大地,王开荣.数值分析[M].北京:科学出版社,2006:47-59.

[6]李炯生.实方阵的正定性[J].数学的实践与认识,1985,15(3):67-73.

[7]雍龙泉,刘三阳,史加荣,等.几类特殊矩阵及性质[J].兰州大学学报:自然科学版,2016,52(3):385-389.

[8]BAI Zhong-zhi,GOLUB G H,NG M K.Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems[J].SIAM Journal on Matrix Analysis and Applications,2003,24(3):603-626.

[9]BAI Zhong-zhi,YANG Xi.On HSS-based iteration methods for weakly nonlinear systems[J].Applied Numerical Mathematics,2009,59(12):2923-2936.

[10]施妙根,顾丽珍.科学和工程计算基础[M].北京:清华大学出版社,1999:108-109.

[11]RYABENKII V S,TSYNKOV S V.A theoretical introduction to numerical analysis[M].Florida:CRC Press,2006:173-194.

[12]陈芳,左军.鞍点问题的HSS-GS迭代法与收敛理论[J].北京信息科技大学学报:自然科学版,2014,29(4):25-29.

[13]吴世良,李翠霞.求解一类复对称线性系统的改进的SNS和SSS迭代法[J].中国科学:数学,2014,44(9):1007-1020.

[责任编辑：魏 强]

Four iterative methods to linear systems

YONG Long-quan

(School of Mathematics and Computer Science, Shaanxi Sci-Tech University,Hanzhong 723000, China)

Four iterative methods to linear systems, such as Jacobi, Gauss-Seidel, HSS, and Richardson iterative, are studied, and sufficient conditions for the convergence of these iterative methods are given. Numerical experiments further show that the size of spectral radius of iterative matrix determines convergence rate in solving large-scale linear systems. Under the premise of spectral radius of iterative matrix less than 1, the smaller the spectral radius, the faster convergence speed.

linear systems;Jacobi iterative;Gauss-Seidel iterative;HSS iteration;Richardson iterative;spectral radius

1673-2944(2016)05-0080-05

2016-06-02

2016-08-08

陕西省教育厅科研基金资助项目(16JK1150)；陕西理工学院科研计划项目(SLGKYQD2-14)

雍龙泉(1980—)，男，陕西省洋县人，陕西理工大学副教授，博士，主要研究方向为优化理论与算法。

O151.2

A