复合函数渐变传输线研究
王 勇,迮天怡,刘 墨
(南京邮电大学,江苏 南京 210023)
复合函数渐变传输线研究
王 勇,迮天怡,刘 墨
(南京邮电大学,江苏 南京 210023)
在已有渐变线类型的基础上,讨论了一种新型的、基于复合函数的渐变传输线,这种复合函数渐变线具有阻抗可调、低反射系数的特点,上述特点正是工业设计应用中所需要的。文章首先给出基于小反射理论的渐变阻抗函数的反射系数响应,然后推导出复合函数的阻抗响应,最后通过实例的方式,仿真出复合函数的阻抗特性和反射系数特性,并与指数渐变函数和三角渐变函数的阻抗特性和反射系数特性进行了比较,发现复合函数具有比指数渐变函数更低的反射系数,阻抗比三角渐变函数更具可调的灵活性。
反射系数;小反射理论;复合函数
0 引言
人们很早就对渐变传输线进行研究和讨论[1-2],伴随着科学技术的不断发展,这种研究与分析也不断的深入,最新的理论成果可从相关文献中获得[3-5]。渐变传输线常用来进行不同类型的传输线之间的转换,或者是不同尺寸传输线之间的过渡。之所以采用渐变线,是因为其具有低驻波、较宽通带等优点。对于工作在微波频段的系统来说,可以采用四分之一阻抗变换器[6],通过离散步进的方式改变阻抗,而另一种更为通用的手段是通过渐变传输线来改变阻抗。在渐变转换的过程中,传输线阻抗连续变化。通过改变渐变的类型就能得到不同的通带特性。常用的渐变线有指数型、三角形和切比雪夫型等[7-11],本文提出了一种基于复合函数的渐变线。这种渐变线可以获得比指数渐变线更低的反射系数,在不改变反射系数的条件下,可任意调节阻抗。
1 基于小反射理论的渐变线的反射系数
考虑如图1所示的连续渐变线,它由一系列长度为Δz的增量节组成,每提升一个长度Δz,它的阻抗都会改变Δz。故而,从z1到z1+Δz处产生的反射系数增量为:

图1 渐变传输线示意图
(1)
在极限的情况下,可以得到准确的微分:
(2)
依据小反射理论[12],即只考虑在每节连接处一次反射的贡献,将其叠加得到总的反射系数。在z=0处的总反射系数可用所有带有适当相移的局部反射求和得出:
(3)
式中θ=2βl,β为相移常数,L为渐变线长度,Z0为传输线特性阻抗。
2 复合函数渐变线的阻抗与反射系数
2.1 指数渐变与三角渐变
首先给出指数渐变的阻抗表达式:
Z(z)=Z0eaz
(4)
将指数渐变的阻抗表达式(4)代入式(3),得到指数渐变的反射系数为:
(5)
当阻抗为式(6)表达式时,
(6)
可以得到三角形渐变的反射系数为:
(7)
2.2 复合函数渐变
对于复合函数渐变而言,有如下假设,当0≤z≤L/2时,令:
(8)
当L/2≤z≤L时,
(9)
式中m、n和k均为正实数。
可以发现,通过调节参数m、n与k中的任意一个参数的取值或者同时调节两个以上参数的取值,便可轻易地改变复合函数的阻抗,获得所需的阻抗值。如表1所示为不同参数m对应的阻抗值。保持n、k为定值并令n=2、k=4、Z0=50 Ω、ZL=100 Ω,通过改变m的取值得到传输线上不同位置的阻抗值。
将式(8)与式(9)带入反射系数表达式(3),得到如下的复合函数渐变反射系数的表达式:
(10)
由式(10)发现,通过调节参数k,复合函数渐变的反射系数可以比指数渐变和三角形渐变更低。当改变参数m和n的取值,而不改变参数k的取值时,可以达到改变阻抗而不改变反射系数的效果。
3 设计实例
用复合函数渐变、三角形渐变与指数渐变,将100 Ω的负载匹配到50 Ω的传输线,画出阻抗变换图与反射系数幅度值。
将Z0=50 Ω、ZL=100 Ω分别代入各自的阻抗表达式,并令复合函数的k=0.7,m=3,n=0.02,得到如图2所示的阻抗变换图。

图2 不同类型渐变阻抗图
而图3则显示在参数k=0.7、m=2、n取不同值时,复合函数的阻抗特性。

图3 复合函数不同n取值阻抗图

表1 不同参数m对应阻抗值 (单位:Ω)
从图3可以发现,调节复合函数的相关参数可以改变阻抗特性。
将特征阻抗、负载阻抗及相关参数代入反射系数的表达式,得到如图4所示的反射系数绝对值曲线。通过图4可以发现,复合函数渐变型具有比指数渐变型、三角渐变型更低的反射系数绝对值,而这正是实际生产中所需要的。
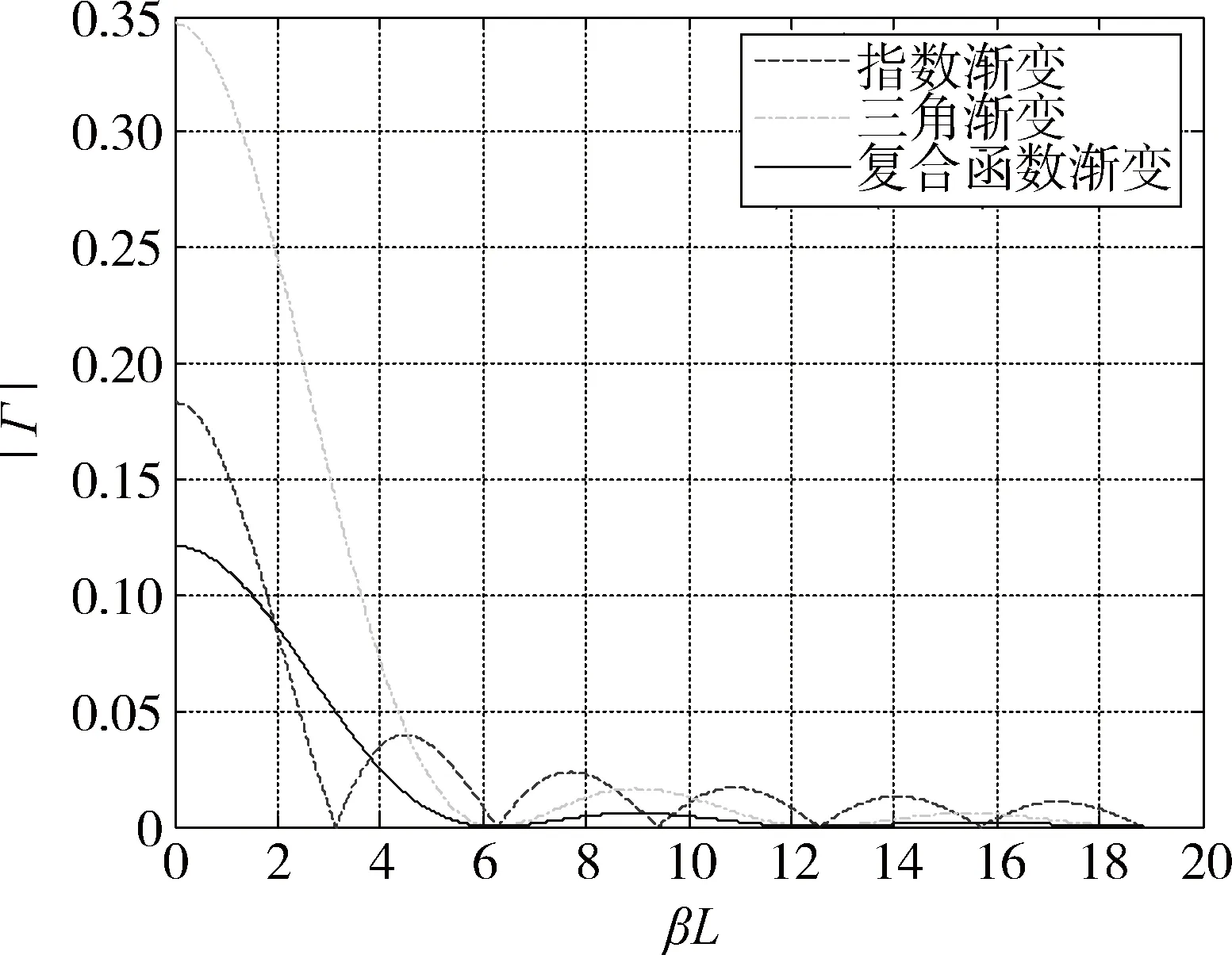
图4 反射系数幅值与频率的关系
图5是调节参数k的不同取值,得到复合函数渐变型的反射系数幅值与频率的关系。
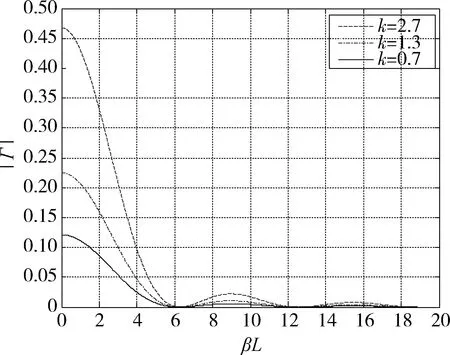
图5 取值k对应反射系数幅值曲线
4 结论
渐变传输线在阻抗匹配中占有重要地位,被广泛应用于各种设计中[13-16],用渐变线可实现小尺寸、宽通带、低驻波和低插损的过渡,在通带范围内具有优良的传输特性。本文详细分析了基于小反射理论的渐变线反射系数,给出了指数渐变型和三角渐变型的阻抗表达式以及反射系数表达式,并提出了复合渐变型的阻抗表达式和反射系数表达式。最后对上述三种渐变型的阻抗和反射系数幅度值进行了仿真研究。研究结果表明,本文给出的复合渐变型可以任意调节阻抗值,获得了比指数型与三角型更好的动态范围,调节参数k的取值,可以获得比三角型更低的反射系数幅度值,这是实际应用中所需要的。
[1] COLLIN R E.The optimum tapered transmission line matching section[J].Proceedings of the IRE,1956,44(4):539-548.
[2] COLLIN R E.Fundations for microwave engineering[M].New York: Mc Graw-Hill,1966.
[3] KILLA A M.Optimum continuous microstrip tapers are amenable to computer aided design[J].Microwave Journal,1983,35(5):221-224.
[4] AHMED M J.Impedance transformation equation for exponential,cosine-squared and parablic tapers transmission line[J].IEEE Transcations on MTT,1981,29(1):647-650.
[5] MAHON J P,ELLIOT R S.Tapered transmission lines with a controlled ripple response[J].IEEE Transcations on MTT,1990,38(10):1546-1550.
[6] LI C,RICKETTS D S.Loss minimization in λ/4 impedance transformers using multipleλ/4-segments[J].Electronics Letters,2013,49(4):274-276.
[7] GROSSBERG M A.Extremely rapid computation of the klopfenstein impedance taper[J].Proceedings of the IEEE,1968,56(9):1629-1630.
[8] KLOPFENSTEIN R W.A transmission line taper of improved design[J].Proceedings of the IRE,1956,44(1):31-35.
[9] 王阳.一种新的渐变线阻抗变换器设计方法[J].电子学报,1992,20(3):88-89.
[10] 周越,张国锋.切比雪夫阻抗变换器的设计方法[J].大学物理,2012,31(11):29-31.
[11] 薛泉.复杂渐变线的分析与综合[J].电子科技大学学报,1994,23(1):28-31.
[12] TORRUNGRUENG D,THIMAPORN C,LAMULTREE S,et al.Theory of small reflections for conjugately characteristic-impedance transmission lines[J].IEEE Microwave & Wireless Components Letters,2008,18(10):659-661.
[13] DARABAN M,PITICA D.Progressive transmission line matching when encountering via mismatching[C].2013 IEEE 19thInternational Symposium for Design and Technology in Electronic Packaging,2013,24:135-138.
[14] SIMION S.Comments on “complex impedance transformers consisting of only transmission-line sections”[J].IEEE Transactions on Microwave Theory and Techniques,2013,61(2):999.
[15] CHEN Y K,BAEYENS Y,CHEN Y K,et al.An 83 GHz high-gain SiGe BiCMOS Power amplifier using transmission-line current-combining technique[J].IEEE Transactions on Microwave theory and Techniques,2013,61(4):1557-1568.
[16] CHUANG M L,WU M T.Dual-frequency impedance transformer with a transmission zero[C].2013 IEEE International Conference on Circuits and Systems,2013:108-110.
Research on tapered transmission line of composite function
Wang Yong,Ze Tianyi,Liu Mo
(Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
This paper discusses a tapered transmission line based on a new composite function.This composite function has the characters of adjustable impedance and the lower reflection coefficient.These characters are necessary in the production of industry.Firstly,this paper gives a discussion about the reflection coefficient of tapered resistance function based on the low-reflection coefficient,and then gives the expression of the response of the composite function.The composite function’s resistance and reflection coefficient is simulated through the examples.At the same time,they are compared with the figure function and the triangular function.We find that the composite function has a lower reflection coefficient than the figure function and a more changeable than the triangular function.
reflection coefficient; theory of small reflections; composite function
TN929
A DOI:10.19358/j.issn.1674-7720.2016.19.021
王勇,迮天怡,刘墨.复合函数渐变传输线研究[J].微型机与应用,2016,35(19):71-73.
2016-05-10)
王勇(1961-),男,博士,教授,主要研究方向:测量与控制及通信网监控。
迮天怡(1991-),男,硕士,主要研究方向:射频通信及嵌入式系统。

