M-H算法的建议分布选择与比较

王丙参,魏艳华

(天水师范学院数学与统计学院,甘肃天水741001)

M-H算法的建议分布选择与比较

王丙参,魏艳华

(天水师范学院数学与统计学院,甘肃天水741001)

文章比较研究了M一H算法与舍选法的联系,给出了建议分布的选择标准与几种建议选择,并比较了这几种建议分布对马氏链的影响,举例说明了M一H算法在贝叶斯推断中可行、稳定、有效。

M一H算法;舍选法;随机数;建议分布;贝叶斯估计

0 引言

随机模拟是研究复杂系统的常用手段,其难点在于目标分布的计算机仿真,即产生目标分布随机数[1]。比如,产生多变量非标准形式且各分量之间相依分布的随机数往往非常困难,难于实现,另外,在不完全数据场合进行统计推断,往往需要产生给定截断分布随机数,但截断分布参数的满条件分布往往没有显示表达式,直接抽样也很难。MCMC方法就是一种解决上述问题的简单有效的贝叶斯计算方法[2,3],而M-H算法是MCMC的核心,已被列为影响工程技术与科学发展的十大算法之首,对其研究具有重要的实际意义[4]。在M-H算法具体操作中,建议分布选择是否恰当直接关系到马氏链的性质,比如混合性、收敛性等,进而影响后面各种统计计算[5,6]。基于此,本文比较研究了M-H算法与舍选法的联系,给出了建议分布的选择标准与几种建议选择,并比较了这几种建议分布对马氏链的影响,举例说明了M-H算法在贝叶斯推断中可行、稳定、有效。

1 对照舍选抽样法研究M-H算法的基本思想与步骤

当某目标密度函数π(x)可被计算,但不易直接抽样时,利用MCMC方法可获得π(x)的一个近似样本,基本思想是[5]:通过构造一个非周期不可约的马氏链{X(t)，t=1，2，…},使其平稳分布恰好为目标分布π(x),这样便可生成近似服从π(x)的样本,从而进行各种统计推断。M-H算法是重要性抽样的实现,也是一种非常通用的构造马氏链方法,它的动机是推广舍选抽样法。在舍选抽样中,有目标分布π(x)、建议概率密度函数q(x)和一个接受准则h(x，y)(概率函数),同样本文也假设π(x)是全样本空间Ω上的目标分布,需要在Ω上产生样本马氏链{x1，…，xt，…},使它的稳定分布恰好为目标分布π(x)。首先,本文令q(x，y)表示由状态x转移到状态y的概率,也常记为q(y|x),称为建议分布或提案分布,则任意选择不可约转移概率q(x，y)及函数0＜α(.，.)≤1,对任意组合(x，y)，x≠y,则:

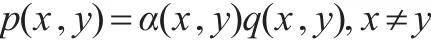
形成一个转移核。注意,建议分布也常常用符号g(x，y)表示。

在t=0时刻,取X(0)=x(0),其中x(0)从初始分布h(x)中抽样且满足π(x(0))＞0。但是,初始点的选择会影响马氏链的性质,因此为了更快达到预期效果,在具体操作时,x(0)一般可取初始估计值,比如矩估计等。接着,给定X(t)=x,首先由q(.|x)产生潜在转移y,然后以概率α(x，y)接受y(X(t+1)=y),以概率1-α(x，y)仍停留在x (X(t+1)=x)。

假设当前状态X(t)=x(t),M-H算法具体步骤如下:

(1)从建议分布q(.|x(t))生成候选值x*。

(4)令t=t+1,返回第(1)步。

注意,M-H比率R(x(t)，x*)总是有定义,这是因为π(x)＞0且q(x，y)＞0。每完成上述一个循环,则生成一个目标分布随机数。在具体实现M-H算法时,可选取多个初始点来检验得到的输出结果是否一致,这也可看作是与最优化算法的结合。显然,在M-H算法中,建议分布的主要目的是产生状态转移,即为每个状态构造一个邻域,并选中邻域中某个邻居状态。要使得M-H算法产生的随机数序列是马氏链,这就需要要求建议分布q(x，y)在整个样本空间Ω上有定义,通常,这是很容易实现的。舍选抽样对所有的x有q(.|x)=q(.),是最简单的情况,但MCMC方法推广了舍选抽样法,使建议分布变成了条件概率密度函数,而M-H算法的神奇之处也正在于此。当然,为了保证马氏链状态产生遍历性的转移,必须要求在x的某个邻域Nx里成立:

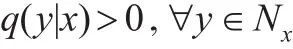
M-H算法接下来要做的是,将选中的状态与当前状态相比,按一定的概率接受其中之一作为随机序列的下一状态。另一个与舍选抽样法不同的是,接受概率不但取决于下一步状态x(t+1),而且和当前状态x(t)有关。

利用因M-H算法产生的随机数序列,保证了X(t+1)只依赖X(t),而和以前产生的随机数无关,所以M-H算法构造的链满足马氏性,即为马氏链,但它是否是非周期不可约的则取决于建议分布q(x，y)的选择。所谓的不可约是指马氏链从任意状态出发都能以一定的正概率转移到其他状态,即它的转移是遍历的。不具有遍历性意味着马氏链的整个状态空间被分割成几个互不相通的子空间,这样,它的子空间的状态就不能迭代到其他子空间中去,进而也不可能存在平稳分布。如果是非周期不可约的,则M-H算法构造的马氏链具有唯一的极限平稳分布,且可以证明M-H算法构造的马氏链以π(x)为其平稳分布。事实上,M-H算法产生的马氏链是可逆的,即:

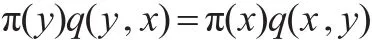
这表示马氏链稳定时,由y→x的量等于由x→y的量,这就导致π(x)为其平稳分布。

利用M-H算法产生样本的主要目的是估计X～π(x)的某一函数的期望。随着t的增大,由M-H马氏链产生随机变量的分布越来越近似该链的平稳分布,故利用这种方法可以估计很多感兴趣的量,如期望Eπ(h(X))、方差varπ(h(X))及尾概率P(X＞a),其中a为很大的数字,由马氏链的极限性质可知,这些量的估计都是强相合的。由于生成的随机数可以重复,并且这些抽样点出现的频率可以修正目标密度与提案分布密度的差异,所以本文应该保留马氏链中的重复值。

但在实际应用中,我们不知道什么时候马氏链才收敛到平稳分布。在M-H算法中,只有在极限情况下才有X(t)～π(x),但是,对于任何迭代都是有限的,不可能得到精确的边际分布,而初始点的选择对马氏链是有影响的。马氏链还未进入稳定阶段之前的状态称为暂态阶段,也可形象称为热机阶段。于是,为了提高估计精度,我们通常舍去马氏链的前D个值,即删除一些初始生成值,也就是所谓的预烧期,但是关于预烧期的选择没有固定的标准,要根据具体情况具体分析,可能很大,比如D=20000,也可能很小,比如D=200。

2 建议分布的选择与比较

通常,我们要求建议分布q(x，y)对于给定的x容易产生q(x，y)的随机数,这样才能使得抽样变得简单方便,否则,这只是将生成目标分布π(x)的困难转移到了生成建议分布的困难,并不能解决问题。另外,一个具有某种特定性质的建议分布可以增强M-H算法的效果,并可直接通过接受概率的大小来反映。关于接受概率,应注意:接受概率要合适,具体问题要具体分布,而不是越大越好,因为太大会导致较慢的收敛性。Gelman等建议,当参数为1维时,接受概率应略小于0.5,当参数大于5维时,接受概率最好为0.25左右[5-7],当然,这只是个人建议,不同的学者可能有不同的看法。

不同的形式建议分布q(x，y)产生了相应的M-H算法变形,下面给出几点具体建议供参考。

(1)M选择:如果对任意的x，y,建议分布都有q(x，y)=q(y，x),即建议分布满足对称性,这时,M-H算法就是Metropolis算法(M算法),此时,接受概率M算法是MCMC方法的最早起源,由N.Metropolis等人于1953年在研究原子与分子的随机运动问题时引入的随机模拟方法。

特别有,如果q(x，y)=q(|x-y|),则成为随机移动M算法。对称建议分布很常用,例如,当给定x,q(x，y)可取正态分布,均值为x,协方差阵为常数阵,一种比较简单的选择就是取正态分布N(x(t)，σ2),关于σ的选择,应注意:由大样本性质,通常后验分布都具有比较好的正态性,因此选择正态分布作为建议分布是合适的,其均值应为上个状态的值,而方差的大小决定了马氏链在参数支撑集上的混合程度,因此σ的选择决定了建议分布的好坏。当增量方差σ太大,大部分候选值被拒绝,这就导致M-H算法的效率太低,而σ太小,大部分候选值被接受,这时得到的马氏链几乎就是随机游动,由于马氏链从一个状态到另一个状态跨度太小,从而无法实现在整个支撑集上的快速移动,进而导致M-H算法的效率不高。可见σ太大或太小都导致M-H算法的效率较低。通常的做法是,在具体抽样时监视候选值的接受概率,Robert,Gelman等建议最好控制在[0.15，0.5]。

(2)独立抽样:如果建议分布q(x，y)与当前状态x无关,即q(x，y)=q(y),则由此建议分布导出的M-H算法称为独立抽样。此时,由建议分布产生一个独立链,抽取的每个候选值都与当前值独立,M-H比率为并且如果g(x)＞0,π(x)＞0,则得到的马氏链就是非周期不可约的。此处,M-H比率也可以表示重要比率,令其中π(x)是目标分布,q(x)为包络分布,则这表明w(x(t))远大于w(x*)的值时,马氏链将会长时间停留在当前值上。进一步,我们有接受概率因此建议分布q(x)应与目标分布π(x)相似,且尾部包含π(x),这样独立抽样的效果才可能好,这也导致独立抽样在实际中很少单独使用。

(3)单变量M-H算法:如果目标分布X是高维的,则直接产生整个X比较困难,这时可以逐个抽取各分量,但是这需要用到完全条件分布。令…，Xn),考虑Xi|X～i,i=1，2，…，n的条件分布,选择适当的转移核q(xi→yi|x～i),对于给定的X～i=x～i产生下一个可能的yi,然后以概率:

(4)随机游动链是通过简单变化M-H算法得到的另一种马氏链,实现方法如下:首先生成ε～h(ε),其中h为密度函数,令x*=x(t)+ε,就可得一个随机游动链。在这种情况下,初始分布g(x*|x(t))=h(x*-x(t))。对于h,一般应选择为正态分布N(0，σ2)、以原点为球心的球面上的均匀分布、尺度变换后的t分布。正态分布的方差可以控制候选值的扩散程度,如果目标分布是双峰分布时,建议选择σ可适当大点,在一般情况下,可令σ=1,即h～N(0，1)可以证明,如果h(x)在0的领域内为正且π(x)的支撑集连通,则生成链是非周期不可约的。

如果建议分布不随时间t而改变,则称M-H算法是齐次的。当然,本文也可构造非齐次的M-H算法,击跑算法就是非齐次的M-H算法的典型代表,在这种方法中,从x(t)出发选择的建议分布由两步产生:先选择移动方向,然后在此方向上产生移动距离。当X的状态空间非常受限,且其他方法很难寻找所有空间的区域时,利用击跑算法可能会取得比较好的效果。遗憾的是,非齐次的M-H算法收敛性质更难确定,甚至无法确定。

3 混合参数贝叶斯估计中M-H算法建议分布的比较

假定y为已知的观测数据,待估参数θ的先验分布为p(θ),则θ的贝叶斯估计往往依赖后验分布p(θ|y)=cL (θ|y)p(θ),其中常数c为归一化常数,未知,L(θ|y)为似然函数。由于在后验分布p(θ|y)中c未知,所以它不能直接用于统计推断,但是本文可利用中M-H算法获得p(θ|y)的近似样本,进而进行各种统计推断。在M-H算法中,常常利用先验分布作为建议分布,即建议分布g(θ)=p(θ),并取MH比率由于先验分布的支撑集覆盖后验分布的支撑集,因此独立链的平稳分布π(θ)即为后验分布p(θ|y)。当然,先验分布的选择会显著影响马氏链的表现,如果选择不合适,则会导致马氏链收敛很慢,达不到预期效果。

假定观测数据y1，…，y100来自混合正态分布:

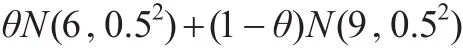
观测数据的直方图见图1,θ的先验分布为U(0，1),本文可利用M-H算法构造平稳分布等于θ的后验分布的马氏链。已知观测数据是由θ=0.7利用合成法生成的,故θ后验密度应该集中在0.7附近,下面考察建议分布对马氏链的影响。

图1 由混合分布θN(6，0.52)+(1-θ)N(9，0.52)生成的100个观测值直方图

(1)利用Beta(1，1)(即U(0，1))作为建议分布,模拟结果如图2。

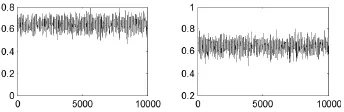
图2 不同初始值θ(1)生成的马氏链轨迹(左图θ(1)=0,右图θ(1)=1)

图2 表明马氏链很快离开初始值,且似乎很容易从θ后验支撑集的各个部分抽取值,这种表现称为混合性良好。为了减少初始值的影响,本文省略前100次迭代,得到:左图均值为0.6467,右图均值为0.6483。可见,无论初始值为0,还是1,马氏链都收敛,且样本均值都与真值0.7非常接近,即模拟效果都不错。

(2)利用Beta(2，10)作为建议分布,模拟结果如图3。

图3 不同初始值θ(1)生成的马氏链轨迹(左图θ(1)=0,右图θ(1)=1)

图3 生成的马氏链慢慢离开初始值,由于摆动明显,显然,此链没有收敛到其平稳分布,只能得到难以令人信服的结果,但是,其后验分布仍是此链的极限分布,故长期运行此链,在原则上是可以估计θ的后验分布。本文同样省略前100次迭代,得到:左图均值为0.5910,右图均值为0.5966。可见,无论初始值为0,还是1,样本均值都与真值0.7的差异比较大。

图2和图3说明建议分布对马氏链的性质影响显著,因此M-H算法的重点在于选择合适的建议分布。

下面考虑用随机游动链生成后验分布。假定候选值θ*=θ(t)+ε,ε～U(-a，a),显然,在马氏链的迭代过程中,候选值有可能落在区间[0，1]外,这就导致迭代过程变得没有实际意义。在这种情况下,本以为迭代结果很差,但是总体而言,迭代结果还是出乎意料的好。在实际操作中,马氏链是如此的神奇,哪怕候选值不在区间[0，1],甚至密度函数值变为负值,迭代结果还是如此完美,仍在0.7附近波动,比如,当a=1时,迭代结果如图4左图所示,本文尝试了很多取值,结果都是如此完美。但是,当a=8时,迭代结果就比较差了,如图4右图所示,这时候选值会经常不在[0，1]区间,但马氏链基本不会接受不合理的候选值,因为不合理的候选值会导致的极大似然函数值变小。

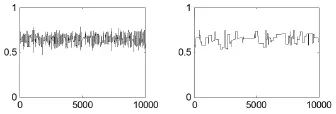
图4 θ*=θ(t)+ε且ε～U(-a，a)生成的马氏链,左图a=1,右图a=8,初始值为0

解决候选值有可能落在区间[0，1]外的一种比较粗糙的解决办法是,当θ∉[0，1]时,重新令后验值为0.5。一个更好的办法是重新参数化。令现在,关于U生成一个随机游动链,候选值u*=u(t)+ε1, ε1～U(-b，b)。下面给出两种看待重新参数化的观点。

(1)在θ空间运行马氏链。这时,建议分布g(.|u(t))要通过变换成为θ空间的建议分布。令|J(θ(t))|表示θ→u变换的Jacobi行列式的绝对值在θ(t)的估值,则候选值θ*的M-H比率为:

(2)在u空间运行马氏链。这时,θ的目标密度要变成u的目标密度,即则候选值U*=u*的M-H比率为:

显然,在图5(左)中,马氏链混合性非常好,但是图5 (右)中,效果就比较差,收敛速度较慢。为了减少初始值的影响,本文省略前100次迭代,得到:左图均值为0.6476,标准差为0.0492,右图均值为0.6502,标准差为0.0435,样本均值都与真值0.7非常接近,右图波动比左图小,注意,这并不代表右图的模拟结果更好,只是表明马氏链混合性不好。

图5 u空间运行马氏链,左图b=1,右图b=10,初始值为0

图6 u空间运行马氏链,b=0.01,左图初始值为0,右图初始值为1

显然,当b=0.01时,不管初始值为0,还是初始值为1,马氏链运行效果都比较差。左图的均值为0.5987,标准差0.0694,均值明显偏离真实值。右图的均值为0.7083,标准差0.0371,读者也许很惊讶,均值竟然更接近0.7,认为模拟结果更好,其实不然,我们不能仅仅从一个偶然的好结果就判定整个方法好,还要考虑结果的产生过程,显然,右图马氏链的收敛性和混合性都很差,模拟效果很差。

在所有方法中,估计值都在0.65附近,比真值0.7偏小,这主要是由于100个特定样本值的性质导致的。

在重新参数化空间生成的随机游动链与原始空间的生成的随机游动链相比,具有很多不一样的性质,重新参数化可以提高马氏链的表现。

[1]王丙参,魏艳华,孙永辉.利用舍选抽样法生成随机数[J].重庆师范大学学报:自然科学版,2013,(6).

[2]魏艳华,王丙参,孙永辉.分组数据场合逆威布尔分布参数贝叶斯估计的混合Gibbs算法[J].四川大学学报:(自然科学版),2014,(1).

[3]魏艳华,王丙参.基于混合Gibbs算法定数截尾逆威布尔分布参数贝叶斯估计[J].统计与决策,2014,(11).

[4]肖柳青,周石鹏.随机模拟方法与应用[M].北京:北京大学出版社, 2014.

[5]Givens GH,Hoeting JA.计算统计[M].王兆军,刘民千,邹长亮等译.北京:人民邮电出版社,2009.

[6]Robert C P,Casella G.Monte Carlo Statistical Methods[M].北京:世界图书出版社,2009.

[7]刘军.科学计算中的蒙特卡罗策略[M].唐年胜,周勇,徐亮译.北京大学出版社,2009.

(责任编辑/亦民)

O212

A

1002-6487(2016)20-0022-04

国家自然科学基金资助项目(61104045);天水师范学院中青年教师科研资助项目(TSA1404)

王丙参(1983—),男,河南南阳人,硕士,讲师,研究方向:金融数学、统计计算。