Rosenau-Kawahara方程的一种空间加权线性守恒差分算法

卓 茹，胡劲松

(西华大学理学院，四川 成都 610039)



·基础学科·

Rosenau-Kawahara方程的一种空间加权线性守恒差分算法

卓 茹，胡劲松*

(西华大学理学院，四川 成都 610039)

对Rosenau-Kawahara方程的初边值问题进行数值研究，利用LAX加权差分格式的构造思想，在保持二阶理论精度的前提下，对空间层引入加权系数θ，提出了一个空间加权线性差分格式。格式合理地模拟了问题的2个守恒性质，证明了差分解的存在唯一性，并利用能量方法分析了格式的二阶收敛性与无条件稳定性。数值实验表明，通过适当地调整选择加权系数θ，可将计算精度显著提高。

Rosenau-Kawahara方程；LAX加权；守恒；收敛性；稳定性

本文考虑如下一类Rosenau-Kawahara方程的初边值问题：

ut+uxxxxt+ux+uxxx-uxxxxx+uux=0，x∈(xL,xR)，t∈(0,T]

(1)

u(x,0)=u0(x)，x∈[xL,xR]，

(2)

u(xL,t)=u(xR,t)=0,ux(xL,t)=ux(xR,t)=0,uxx(xL,t)=uxx(xR,t)=0,t∈[0,T]。

(3)

其中，u0(x)是已知光滑函数。在描述紧离散系统的动力学行为时，Rosenau-Kawahara方程(1)可以看作是Rosenau方程[1-3]、KdV方程[4-6]和Kawahara方程[7-8]的推广形式。在对非线性波的研究中，文献[9]首先讨论了其孤波解和周期解，文献[10-12]又进一步给出了带通常的幂指数非线性项的广义Rosenau-Kawahara方程的孤波解以及2个守恒量：

(4)

(5)

1 差分格式及守恒律

(6)

(7)

(8)

Qn-1=…=Q0，

(9)

En-1=…=E0。

(10)

证明 将式(6)两端乘以h然后对j从1到J-1求和，根据边界条件(8)和分部求和公式[15]，经计算得

(11)

根据Qn的定义，由式(11)递推可得式(9)。

(12)

其中，

由边界条件(8)和分部求和公式[15]得：

(13)

(14)

(15)

将式(13)—(15)代入式(12)有

(16)

由En的定义，对式(16)递推可得式(10)。

2 差分格式的可解性

证明 应用数学归纳法。显然U0由初值条件(7)确定，先用具有二阶精度的C-N格式[13]计算出U1，即U0和U1是唯一确定的。假设U0，U1，…，Un(n≤N-1)是唯一可解的，现考虑方程(6)中的Un+1：

(17)

将式(17)与Un+1做内积，得到

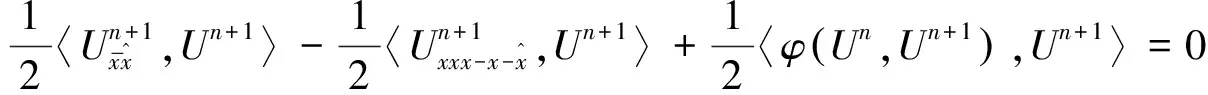
(18)

类似式(13)有

(19)

又

(20)

(21)

将式(19)—(21)代入(18)得到

(22)

又直接利用Cauchy-Schwarz不等式得到

(23)

将式(23)代入式(22)得

3 差分格式的收敛性和稳定性

令差分格式(6)—(8)的截断误差为

(24)

‖u‖L2≤C, ‖ux‖L2≤C, ‖uxx‖L2≤C, ‖u‖≤C, ‖ux‖≤C。

证明 由离散守恒律式(10)可知，En=E0≤C，再利用Cauchy-Schwarz不等式，有

整理得

由Cauchy-Schwarz不等式

(25)

注：定理3表明，差分格式(6)—(8)的解Un以‖·‖无条件稳定。

(26)

(27)

类似于式(13)、(14)，有:

(28)

(29)

再由引理1和定理3，以及Cauchy-Schwarz不等式，有

(30)

又

(31)

将式(28)—(31)代入式(27)，并注意到式(25)，整理得

(32)

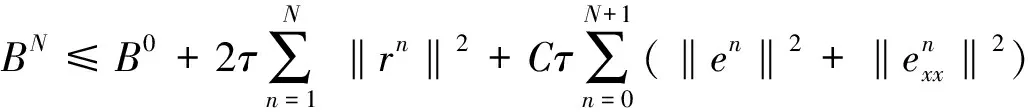
(33)

其中

(34)

由B0≤Ο(h2+τ2)2,再将式(33)和式(34)整理得

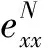
类似式(25)，得

最后根据离散的Sobolve不等式[15],得到

‖eN‖≤O(τ2+h2)。

4 数值实验

在数值实验中，为了便于和文献[13]中的线性格式做比较，故选取文献[13]中的数值算例进行数值模拟实验，即

图1 τ=h=0.1，参数θ变化时，最大模误差变化曲线

图2 τ=h=0.05，参数θ变化时，最大模误差变化曲线

图3 τ=h=0.025，参数θ变化时，最大模误差变化曲线

tQnEnθ=0．5θ=0．75θ=1θ=1．25θ=0．5θ=0．75θ=1θ=1．2504．120893184．120893214．120893244．120899500．836167110．836184100．836201090．83620118204．120893094．120893064．120893034．120899170．836167110．836184100．836201090．83620120404．120895614．120894314．120892994．120898980．836167110．836184100．836201090．83620121

表2 对不同θ，在几个不同时刻的En和Qn(τ=h=0.05)

表3 对不同θ，在几个不同时刻的En和Qn(τ=h=0.025)

[1]Rosenau P . A Quasi-continuous Description of a Nonlinear Transmission Line[J]. Physical Scripta, 1986,34:827.

[2]Rosenau P. Dynamics of Dense Discrete Systems[J].Progress of Theoretical Physics, 1988,79: 1028.

[3]Park M A . On the Rosenau Equation[J]. Applied Mathematics and Computation,1990,9(2):145.

[4]Cui yanfen, Mao De-kang. Numerical Method Satisfying the First Two Conservation Laws for the Korteweg-de Vries Equation [J].Journal of Computational Physics,2007,227(1): 376.

[5]Zhu Shaohong, Zhao Jennifer. The Alternating Segment Explicit-Implicit Scheme for the Dispersive Equation[J]. Applied Mathematics Letters, 2001,14(6):657.

[6]Özer S, Kutluay S. An Analytical-numerical Method for Solving the Korteweg-de Vries Equation [J]. Applied Mathematics and Computation,2005, 164 (3): 789.

[7]陶双平,崔尚斌. 非线性Kawahara方程解的存在唯一性[J]. 数学年刊A辑,2002,23(2):221.

[8]孙小春. Kawahara方程初值问题解的整体存在性[D]. 兰州：西北师范大学，2007.

[9]Zuo Jinming. Solitons and Periodic Solutions for the Rosenau-KdV and Rosenau-Kawahara Equations[J]. Applied Mathematics and Computation,2009,215(2):835.

[10]Biswas L M. Application of He’s Principles to Rosenau-Kawahara Equation[J]. Mathematics in Engineering,Science and Aerospace MESA,2009,2(2):183.

[11]Biswas A, Triki H, Labidi M. Bright and Dark Solitons of the Rosenau-Kawahara Equation with Power Law Nonlinearity[J].Physics of Wave Phenomena,2011,19(1):24.

[12]胡劲松,王玉兰,王正华.广义Rosenau-Kawahar方程的孤波解及其守恒律[J].西华大学学报(自然科学版)，2013,32(3):26.

[13]Hu J, Xu Y,Hu B,et al. Two Conservative Difference Schemes for Rosenau-Kawahara Equation[J]. Advances in Mathematical Physics,2014(2014),Article ID 217393,11 pages.

[14]陈涛,胡劲松.求解广义 Rosenau‐Kawahara 方程的一个守恒差分格式[J]. 西北师范大学学报(自然科学版)，2015,51(5):18.

[15]Zhou Yulin. Application of Discrete Functional Analysis to the Finite Difference Methods[M]. Beijing ：International Academic Publishers, 1991.

(编校：叶超)

A Weighted Linear Conservative Finite Difference Scheme forRosenau-Kawahara Equation

ZHUO Ru, HU Jinsong*

(School of Science, Xihua University, Chengdu 610039 China)

In this paper, a linear conservation finite difference scheme with one weighted coefficient is designed by LAX scheme. The scheme has the advantages that it preserves some invariant properties of the original differential equation. It simulated the conservation properties of the problem well. The prior estimate, existence and uniqueness of the finite difference solution were also obtained. It was proved that the finite difference scheme is convergent with second-order and unconditionally stable by energy method. Numerical experiment result shows that appropriate adjustments to the weighted parameters would significantly improve the computational accuracy.

Rosenau-Kawahara equation； LAX weighted； conservation； convergence；stability

2015-11-28

四川省基础应用研究项目(2013JY0096)；西华大学重点基金项目(Z1513324)。

O241.82

A

1673-159X(2016)05-0084-8

10.3969/j.issn.1673-159X.2016.05.016

*通信作者：胡劲松(1973—)，男，教授，博士，主要研究方向为微分方程数值解。E-mail:hjs888hjs@163.com.