带扰动的梁方程非线性边值问题正解的唯一性
古传运,刘 浏,王园园
(1.四川文理学院数学学院,四川 达州 635000; 2.达州市经济与信息化委员会, 四川 达州 635000)
·基础学科·
带扰动的梁方程非线性边值问题正解的唯一性
古传运1,刘 浏1,王园园2
(1.四川文理学院数学学院,四川 达州 635000; 2.达州市经济与信息化委员会, 四川 达州 635000)
研究一类带扰动的滑动固定梁方程非线性边值问题。用混合单调算子新的不动点定理,得到所研究方程正解的存在唯一性,改进和推广了前人的工作。举例应用了所得的主要结果。
梁方程; 非线性边值问题; 正解; 存在唯一性;混合单调算子;不动点定理
近年来,利用具有不同边值条件的四阶微分方程模拟弹性梁的弯曲平衡问题已经被许多学者所研究,大多数所考虑的是具有零边值条件的非线性方程[1-9]。当边值条件是非零或非线性时,四阶微分方程能够模拟其末端搁在弹性支座上的梁[10-14]。
文献[12]利用单调迭代方法研究了一类滑动固定梁方程非线性边值问题
单调正解的存在性,其中f∈C([0,1]×R2),g∈C(R)(如图1所示)。

图1 示意图
受此启发,本文将利用带有扰动的混合单调算子的不动点定理,研究一类带扰动的滑动固定梁方程非线性边值问题
(1)
正解的存在唯一性,其中0 引理 1[12]方程(1)和下面的方程等价: 这里 (2) 和 引理 2 函数H(t,s)和ψ(t)的性质如下: (3) 证明 当0≤s≤t≤1时, 当0≤t≤s≤1时, 当t∈[0,1]时, 假设(E,‖·‖)是Banach 空间,P是E中的闭凸非空子集,θ是E中的零元素。若P成立(i)x∈P, λ≥0⟹λx∈P;( ii)x∈P,-x∈P⟹x=θ,则称P为E中的一个锥。由P引出E中的半序关系如下:x,y∈E,x≤y当且仅当y-x∈P。若x≤y且x≠y, 则记作x 记P0={x∈P|x为P的内点}, 如果P0非空,则称锥P为体锥; 若存在常数N>0,使得对任意x,y∈E,θ≤x≤y,都有‖x‖≤N‖y‖,则称锥P是正规的, 其中N叫做锥P的正规常数。 任意x,y∈E,若存在λ>0和μ>0,使得λx≤y≤μx,则记作x~y。显然 ~ 是一个等价关系。 给定w>θ, 记Pw={x∈E|x~w},易知当∀w∈P,有Pw⊂P且当w∈P0时,Pw=P0。 定义1[15]若∀x,y∈E,x≤y,有Ax≤Ay(或Ax≥Ay),则称算子A:E→E递增(或递减)。 定义2[15]若A(x,y)满足xi,yi(i=1,2)∈P,x1≤x2,y1≥y2有A(x1,y1)≤A(x2,y2),则称A(x,y)是混合单调算子。如果A(x*,x*)=x*,称x*∈P是A的不动点;又若x*>θ,则称x*是A的正不动点。 定义3[15]A:P→P称为次齐次算子,如果A满足 A(tx)≥tA(x),∀t∈(0,1),x∈P。 (4) 引理3[15]设w>θ,β∈(0,1),A:P×P→P是混合单调算子且满足 A(tx,t-1y)≥tβA(x,y),∀t∈(0,1),x,y∈P , (5) 和B:P→P是次齐次递增算子。若 (i)有w0∈Pw成立A(w0,w0)∈Pw和Bw0∈Pw, 则: 1)A:Pw×Pw→Pw,B:Pw→Pw; 2)存在u0,v0∈Pw和r∈(0,1)则有 rv0≤u0 3)算子方程A(x,x)+Bx=x在Pw中存在唯一解x*; 4)对任意初值x0,y0∈Pw,构造迭代序列 xn=A(xn-1,yn-1)+Bxn-1,yn=A(yn-1,xn-1)+Byn-1,n=1,2,..., 注 1[15]: 若B是零算子, 则引理 3 也成立。 令P={x∈C[0,1]|x(t)≥0,t∈[0,1]},易知P是Banach空间C[0,1]中正规锥。 斯库特学会了从别人的角度看问题。她站在拉德利家的前廊上第一次从拉德利家的角度环顾她再熟悉不过的街区。真正体会到了父亲的话。那一刻,她真正成长了,拉德利不再是怪人,而是那个在寒夜里悄悄为她披上毯子的热心邻居。他偷偷缝好了杰姆试图偷窥他被发现而不得不丢弃的裤子,虽然针脚歪歪扭扭,他送给孩子们他自己用香皂精心刻成的长得像杰姆和斯库特的娃娃,一只心爱的怀表,两枚自己珍藏的古董吉祥币,还有他最最宝贵的生命。在她眼中,拉德利是一位真正的绅士。 假设: (H3) 存在一个常数β∈(0,1)使得 f(t,λu,λ-1v)≥λβf(t,u,v),∀t∈[0,1],λ∈(0,1),u,v∈[0,) 和 h(t,μu)≥μh(t,u),∀t∈[0,1],μ∈(0,1),u∈[0,); (H4) 存在一个常数δ0>0使得f(t,u,v)≥δ0h(t,u),∀t∈[0,1],u,v∈[0,+)。 定理1 若假设(H1)—(H4)成立,则: 1)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0 其中,w(t)=t2,t∈[0,1]。 2)问题(1)在Pw中存在唯一正解u*。 3)对任意初值x0,y0∈Pw,能构造迭代序列 证明 定义两个算子A:P×P→E和B:P→E为 由引理1, 易证u是问题(1)的一个解当且仅当u=A(u,u)+Bu,即u是算子A+B的不动点。 由条件(H1), 可知A:P×P→P 和B:P→P。进一步,由条件(H2),可验证算子A是混合单调算子和算子B递增。 另一方面, 对任意λ∈(0,1)和u,v∈P,由(H3)可知 A(λu,λ-1v)(t)= λβA(u,v)(t)。 即对于λ∈(0,1),u,v∈P,有A(λu,λ-1v)≥λβA(u,v),所以算子A满足条件(5)。同理由(H3)可知,对任意μ∈(0,1)和u∈P, 即对于μ∈(0,1), u∈P,有B(μu)≥μBu,所以算子B是一个次齐次算子。 接下来证明A(w,w)∈Pw和Bw∈Pw, 其中w(t)=t2,t∈[0,1]。 由引理2和条件(H1),(H2),对于∀t∈[0,1],则有: 因此,对∀t∈[0,1],有 从条件(H1)和(H4),可知 因此有A(w,w)∈Pw。类似可证,对∀t∈[0,1],有 易知Bw∈Pw,故引理3的条件(i)满足。 下面证明引理3的条件(ii) 也满足。 对∀t∈[0,1],u,v∈P,由条件(H4), δ0Bu(t)。. 即,对 ∀t∈[0,1],u,v∈P有A(u,v)≥δ0Bu;因此利用引理3可得定理1的结论。 (I)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0 其中w(t)=t2,t∈[0,1]; (II)非线性边值问题 在Pw中存在唯一正解u*; (III)对任意初值x0,y0∈Pw,构造一迭代序列 注2:由注1和定理1, 推论易证。 最后举一例说明定理1。 例 考虑下述非线性边值问题: (6) 其中g(u(1))<0。令 再者,我们取δ0=1, 则有 所以(H4)成立。由定理1知,方程(6)在Pw中有唯一正解u*, 其中w(t)=t2,t∈[0,1]。 [1]Daniel F, Donal O, Juan P. Fourth-order Problems with Nonlinear Boundary Conditions [J]. Journal of Computational and Applied Mathematics ,2005, 174:315. [2]Qingliu Yao. Monotonically Iterative Method of Nonlinear Cantilever Beam Equations [J]. Applied Mathematics and Computation, 2008, 205: 432. [3]Xiaoping Zhang. Existence and Iteration of Monotone Positive Solutions for an Elastic Beam Equation with a Corner [J]. Nonlinear Analysis: Real World Applications, 2009, 10:2097. [4]庞彦瓦. 一类四阶微分方程边值问题解的存在唯一性[J]. 长春师范学院学报(自然科学版),2009,28(4):1. [5]Alberto Cabada, Ricardo Roque Enguiça. Positive Solutions of Fourth Order Problems with Clamped Beam Boundary Conditions [J]. Nonlinear Analysis,2011, 74: 3112. [6]王珍燕. 带2个参数四阶边值问题的正解及多个正解的存在性[J]. 烟台大学学报(自然科学与工程版), 2012, 25(1):9. [7]张艳红. 含有一阶导数的四阶边值问题的正解[J]. 苏州大学学报(自然科学版),2012, 28(1):7. [8]吴湘云. 一类梁方程边值问题正解的存在性[J]. 山东科学,2012, 25(5):6. [9]Wang Kun, Yang Zhilin. Positive Solutions for a Fourth-Order Boundary Value Problem [J]. Journal of Mathematic, 2013(8):1. [10]To Fu MA. Positive Solutions for a Beam Equation on a Nonlinear Elastic Foundation [J]. Mathematical and Computer Modelling, 2004, 39: 1195. [11]To Fu Ma, Jair da Silva. Iterative Solutions for a Beam Equation with Nonlinear Boundary Conditions of Third Order [J]. Applied Mathematics and Computation,2004, 159: 11. [12]Edson Alves, To Fu Ma, Maurício Luciano Pelicer. Monotone Positive Solutions for a Fourth Order Equation with Nonlinear Boundary Conditions [J]. Nonlinear Analysis, 2009,71:3834. [13]Li Shunyong , Zhang Xiaoqin. Existence and Uniqueness of Monotone Positive Solutions for an Elastic Beam Equation with Nonlinear Boundary Conditions [J]. Computers and Mathematics with Applications,2012,63: 1355. [14]Mohamed Jleli, Bessem Samet. Existence and Uniqueness of Positive Solutions to a Fourth-order Two-point Boundary-value Problem [J]. Electronic Journal of Differential Equations, 2013(173):1. [15]Zhai C B, Hao M R. Fixed Point Theorems for Mixed Monotone Operators with Perturbation and Applications to Fractional Differential Equation Boundary Value Problems [J]. Nonlinear Anal,2012, 75:2542. (编校:叶超) The Uniqueness of Positive Solutions for Beam Equations with Perturbed Nonlinear Boundary Value Problem GU Chuanyun1, LIU Liu1, WANG Yuanyuan2 (1.School of Mathematics, Sichuan University of Arts and Science, Dazhou 635000 China;2.Dazhou City Provincial Economic and Information Commission, Dazhou 635000 China) This work is concerned with the nonlinear boundary value problem of a class of beam equations with perturbed. Its existence and uniqueness of positive solutions were obtained by using a new fixed point theorem for mixed monotone operators. The result here improves and generalizes the predecessors’ work. Finally, the example was given to illustrate the main result. beam equation; nonlinear boundary value problem; positive solution; existence and uniqueness; mixed monotone operator; fixed point theorem 2015-05-26 四川省教育厅科研项目(14ZB0309);四川文理学院面上项目(2014Z010Y)。 古传运(1982—),男, 讲师,硕士,主要研究方向为非线性泛函分析和微分方程。 O175.8 A 1673-159X(2016)05-0092-6 10.3969/j.issn.1673-159X.2016.05.0171 基本事实和初步结果
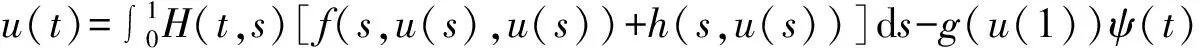
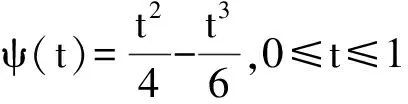






2 主要结论







3 应用





