分数阶模糊时滞神经网络模型解的存在唯一性和有限时间稳定性

哈金才,杨洪福,张启敏

(北方民族大学数学与信息科学学院,宁夏银川750021)

分数阶模糊时滞神经网络模型解的存在唯一性和有限时间稳定性

哈金才,杨洪福,张启敏

(北方民族大学数学与信息科学学院,宁夏银川750021)

本文介绍了一类分数阶模糊时滞神经网络模型.利用压缩映射原理,讨论了带时滞的分数阶神经网络模型解的存在性和唯一性,并根据Gronwall不等式结合分数阶微分方程的性质,证明了分数阶神经网络模型平衡点的有限时间稳定性,给出了有限时间稳定性的判断准则.最后,给出数值仿真说明了理论结果的正确性.

分数阶模糊神经网络;存在性;唯一性;有限时间稳定性

1　引言

近几年来,由于分数阶系统可应用于许多科学和工程领域,因此分数阶微积分模型受到人们越来越多的关注[1-10].文献[3-6,9]表明记忆效果(分数微分或积分算子)用到一个神经网络系统是一个非常重要的改进.

另一方面,微分方程的稳定性分析一直是最重要的动力学行为,与古典的李雅普诺夫稳定相比较,有限时间稳定更符合实际需要.然而,关于时滞分数阶模糊神经网络模型还没有这方面的讨论.本文考虑如下带有时滞的分数阶模糊神经网络模型:

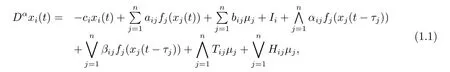
其中t∈T=[0,T],i∈ℵ={1,2,···,n},n是神经元的个数,xi(t)表示第i个神经元在t时刻的状态变量;αij,βij分别表示模糊反馈最小和最大模块的链接权重;Tij及Hij分别表示模糊前向最小和最大模块的联接权重;aij表示第j个神经元与第i个神经元的联接权重;bij表示自由向前模块;∧,∨分别表示模糊与(取小)和模糊或(取大)算子;µi,Ii分别表示第i个神经元的输入和偏差;ci＞0表示网络不连通和无外部附加电压差时第i个神经元恢复独立静息状态的速率;fj(·)为激活函数;τj≥0表示沿轴突的第j个神经元的传输延迟.

系统(1.1)的初始条件为

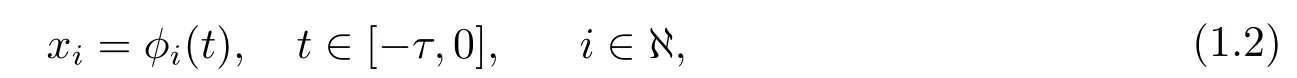
其中

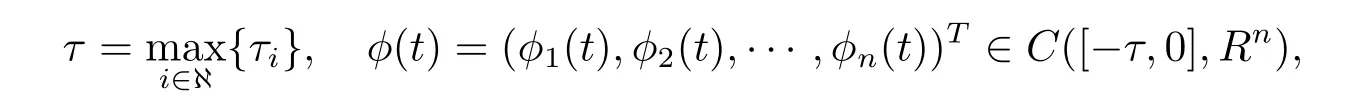
这里C([-τ,0],Rn)表示所有从[-τ,0]到Rn的连续函数组成的全体.定义范数为‖|φ|‖=‖φ(t)‖,其中‖φ(t)‖=|φi(t)|.为了证明方便,定义如下符号

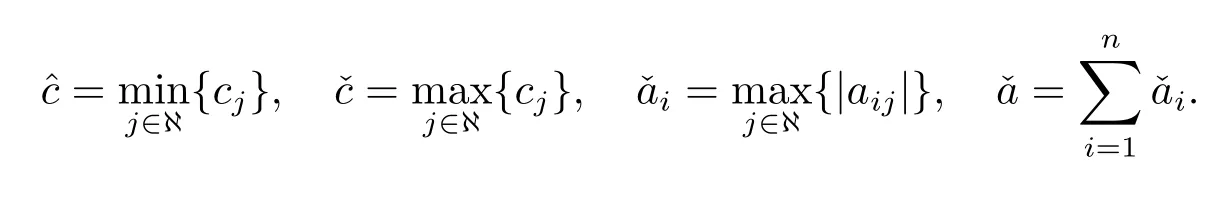
2　预备知识

定义2.1[1,3]函数f的α分数阶积分定义为

其中t≥t0且α＞0,Γ(·)为Gamma函数,Γ(s)=

定义2.2[1,5]函数f的α阶Caputo分数阶微分定义为

其中t≥t0.m是一个正整数满足m-1＜α＜m.特殊地,当0＜α＜1时,

定义2.3[7,8]对任意t∈[0,+∞),如果常量x∗=()T∈Rn满足

则称x∗为系统(1.1)的平衡点.

定义2.4[9,10]若系统(1.1)的平衡点x∗=()T关于{t0,δ,ε,T,τ}是有限时间稳定,则对任意常数ε＞0,都能找到0＜δ＜ε,使得当初始值(1.2)满足‖|φ-x∗|‖＜δ时,系统(1.1)的任意解x(t)=(x1(t),x2(t),···,xn(t))T有‖x(t)-x∗‖＜ε,∀t∈T=[t0,t0+T].

引理2.1[2,4]若x(t)∈Cm([0,∞),Rn),且m-1＜α＜m∈Z+,则有

(1)IαIβx(t)=Iα+βx(t),α,β≥0,

(2)DαIαx(t)=x(t),α≥0,

(3)IαDαx(t)=x(t)-x(j)(0),α≥0.

引理2.2[11]对任意的αij,βij∈R及i,j∈ℵ,如下结论成立:

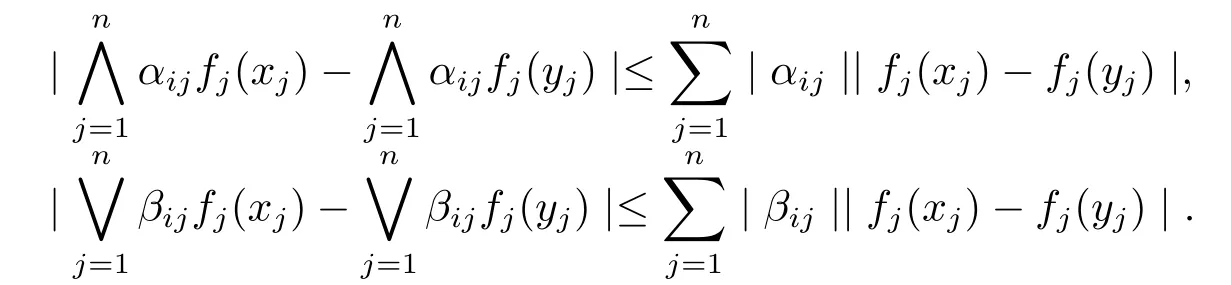
引理2.3[12]若κ1,κ2,···,κd是非负实数,d∈Z+,因此对任意的λ＞1,有

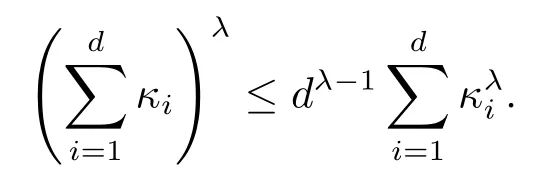
为了证明本文的主要结果,对分数阶神经网络模型(1.1)给出如下假设:

(H1)激活函数fj(·)满足Lipschitz条件,即存在Lj＞0,使得

(H2)对于ci,aij,αij,βij和Lj,满足如下不等式(++)＜.

3　分数阶模糊神经网络模型解的存在唯一性

为了讨论分数阶神经网络系统(1.1)解的存在性与唯一性,先给出如下定理.

定理3.1如果假设(H1)和(H2)成立,则系统(1.1)存在唯一的平衡点x∗.

证首先,构造一个映射Θ:Rn→Rn满足

其中Θ(u)=(Θ1(u1),Θ2(u2),···,Θn(un))T.对于任意两个不同的向量u=(u1,u2,···,un)T和v=(v1,v2,···,vn)T,有

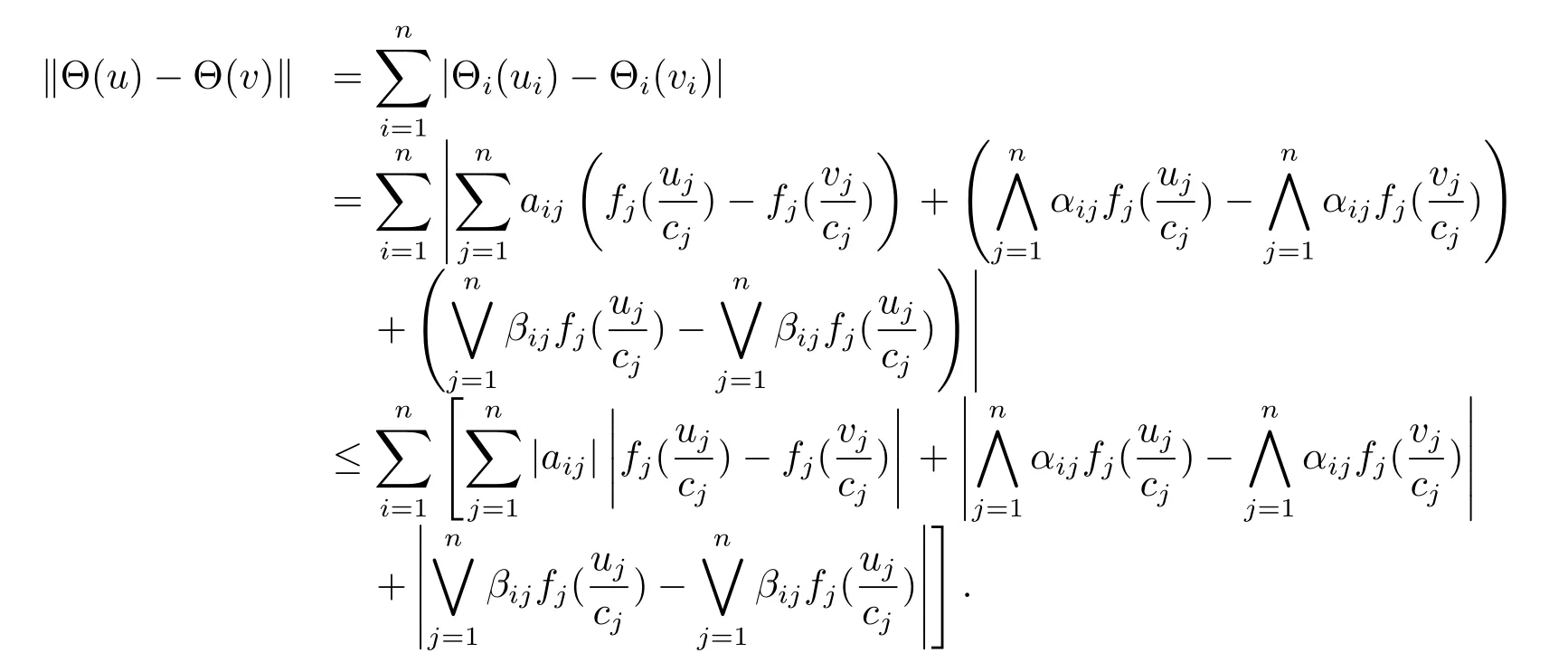
根据引理2.2和假设(H1),可得

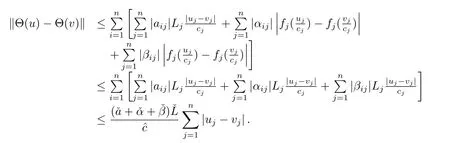
从假设条件(H2),有

由(3.2)式可知Θ:Rn→Rn是压缩映射.故存在唯一不动点u∗∈Rn使得Θ(u∗)=u∗.即

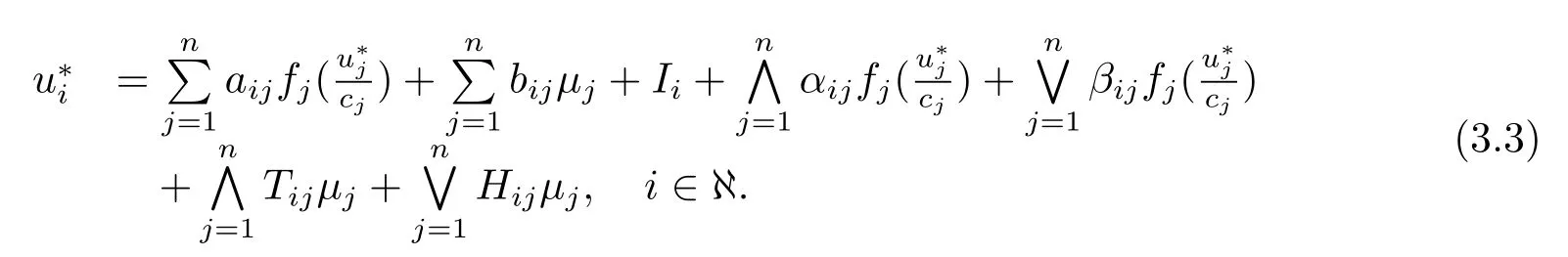
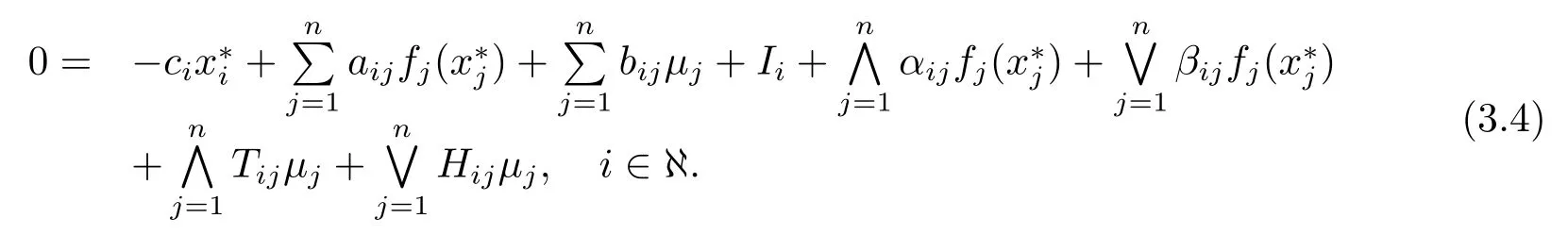
因为u∗是唯一的不动点,因此分数阶系统(1.1)有唯一的平衡点x∗.

定理3.2如果定理3.1中的假设成立,且系统(1.1)的解x(t)∈C([0,T],Rn)满足初始条件,则系统(1.1)存在唯一解x(t).

证证明与定理3.1类似,略.

4　分数阶模糊神经网络模型的有限时间稳定性

本节应用定理3.1和定理3.2讨论分数阶神经网络系统(1.1)解的稳定性.

定理4.1当0.5≤α＜1时,如果假设(H1)和(H2)成立,并且满足不等式

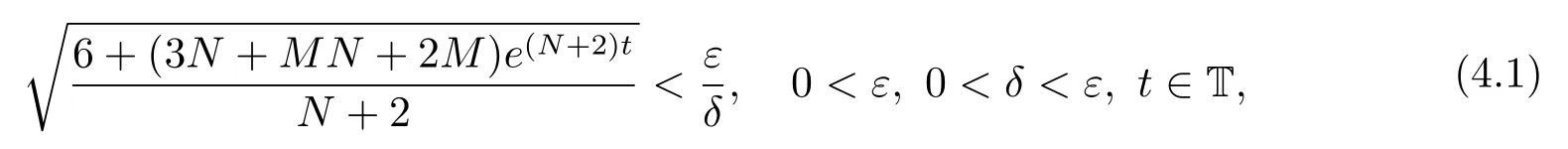
其中

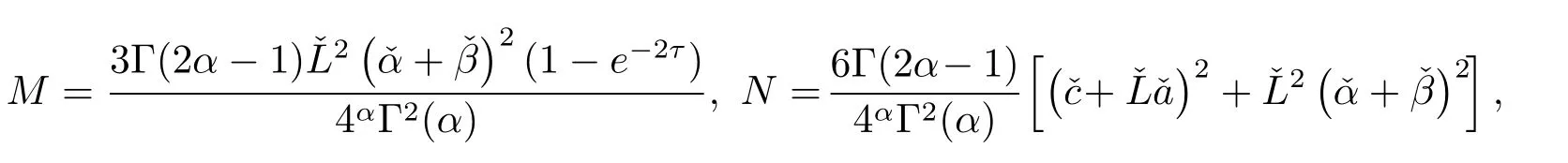
则(1.1)式的唯一平衡点x∗=()关于{t0=0,δ,ε,T=[0,T],τ}是有限时间稳定.

证设x(t)=(x1(t),x2(t),···,xn(t))T是系统(1.1)的任意解,因此有

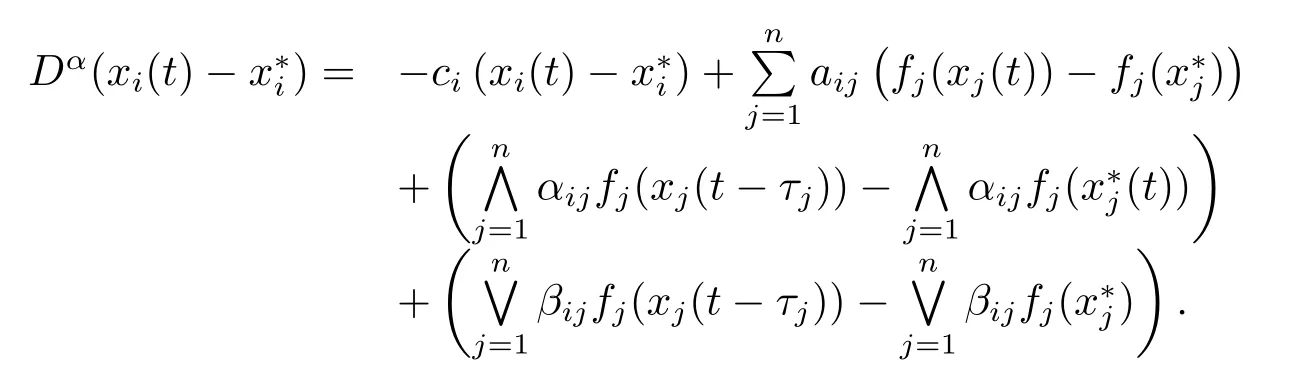
通过引理2.1,可得出如下方程

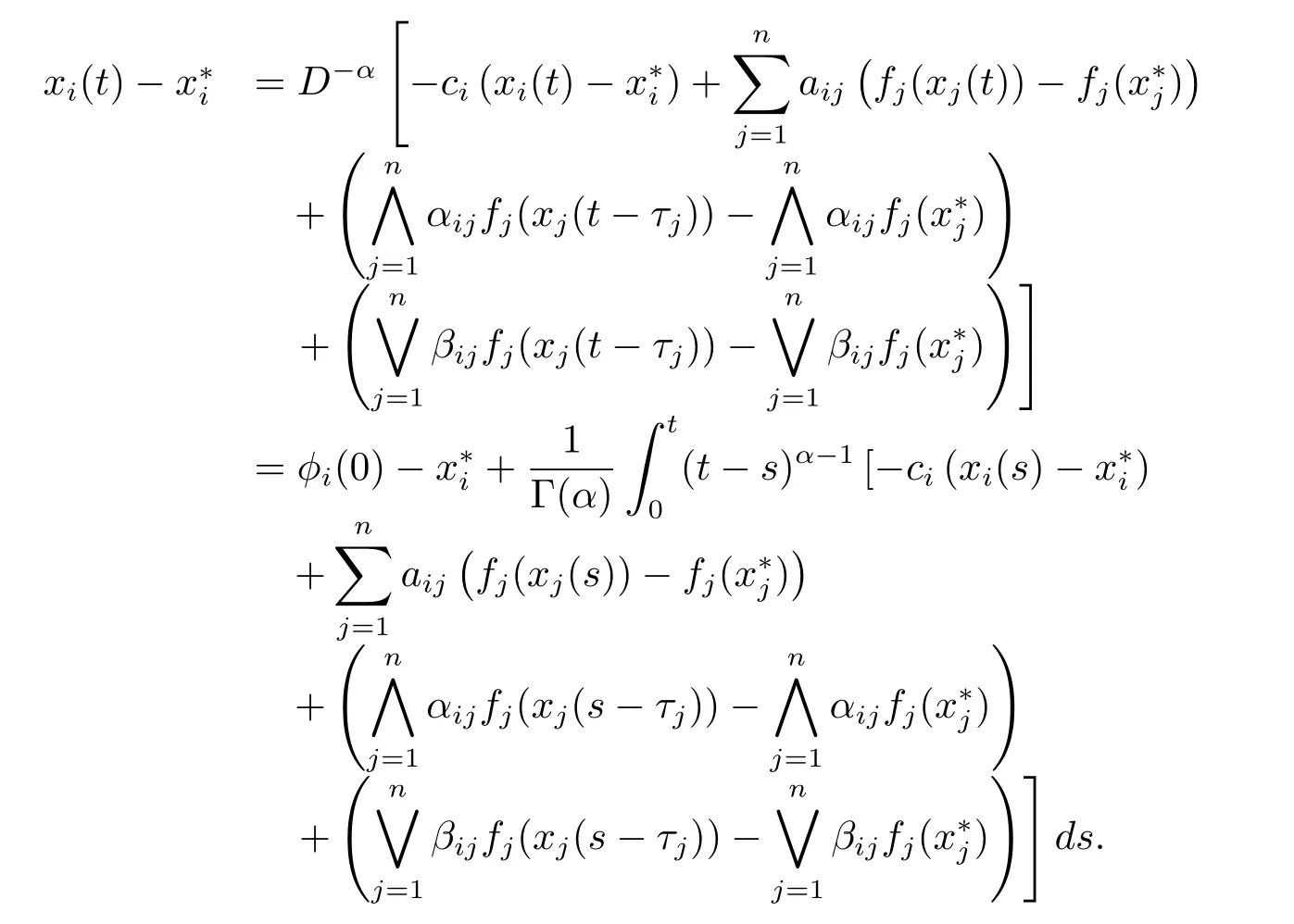
根据引理2.2,再由假设(H1)和范数‖·‖的性质,显然有

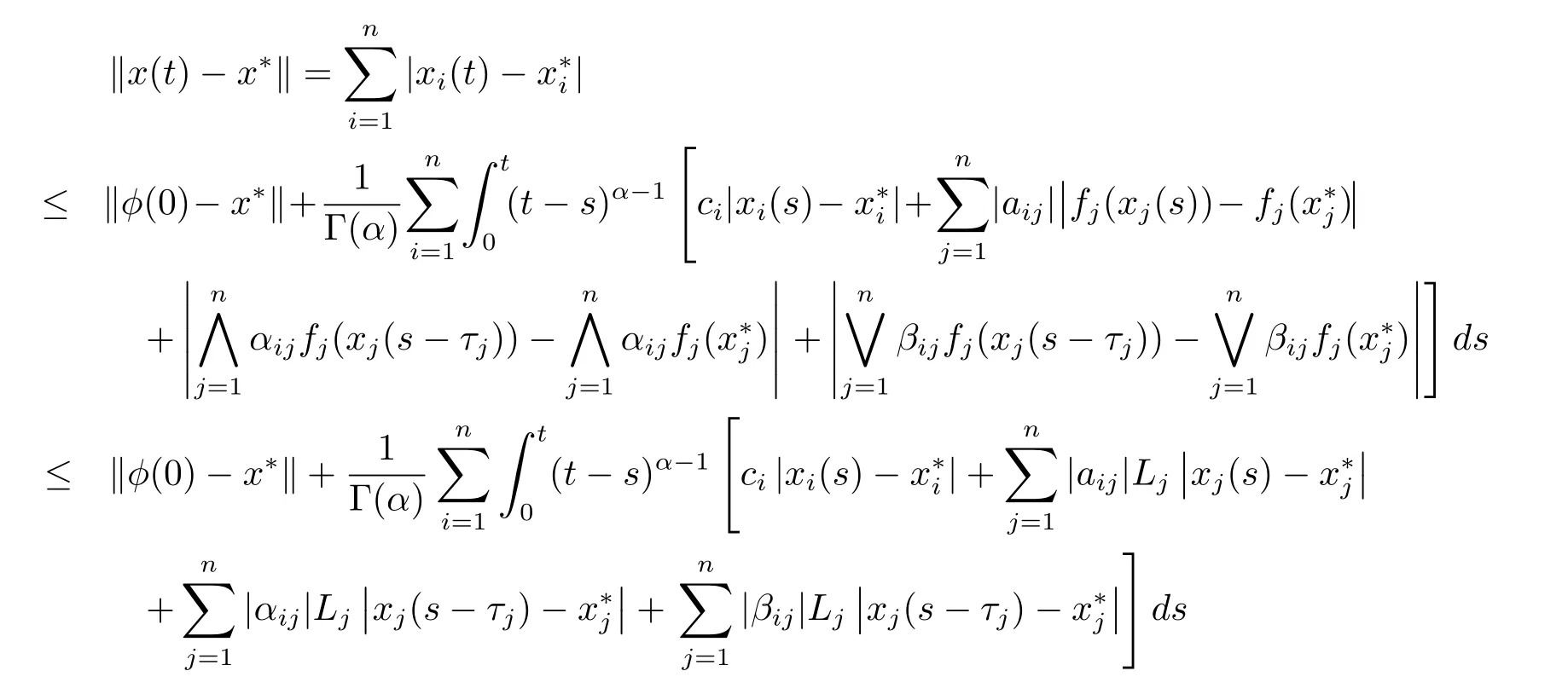
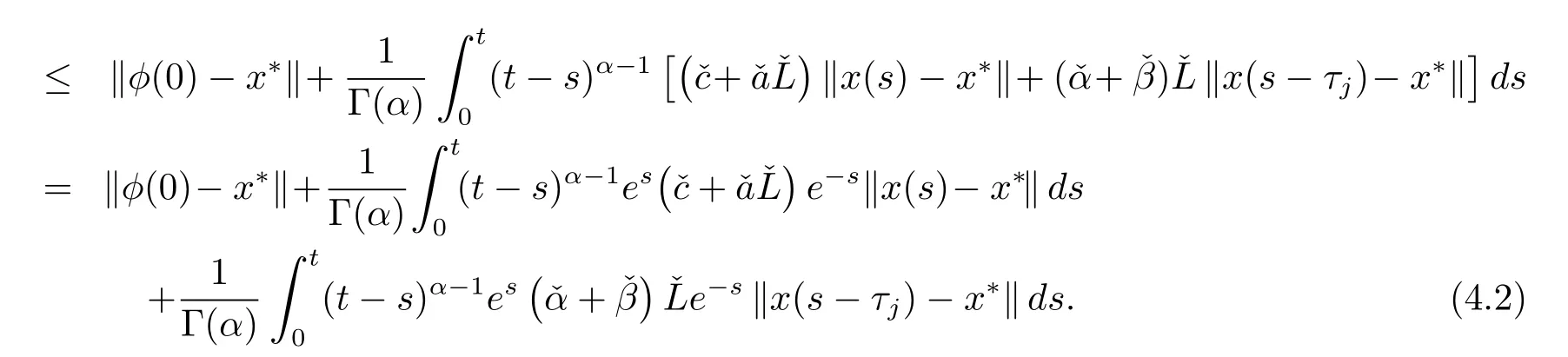
对(4.2)式应用Cauchy-Schwartz不等式,可得

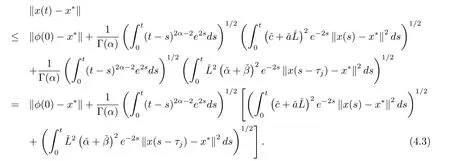
另一方面,有

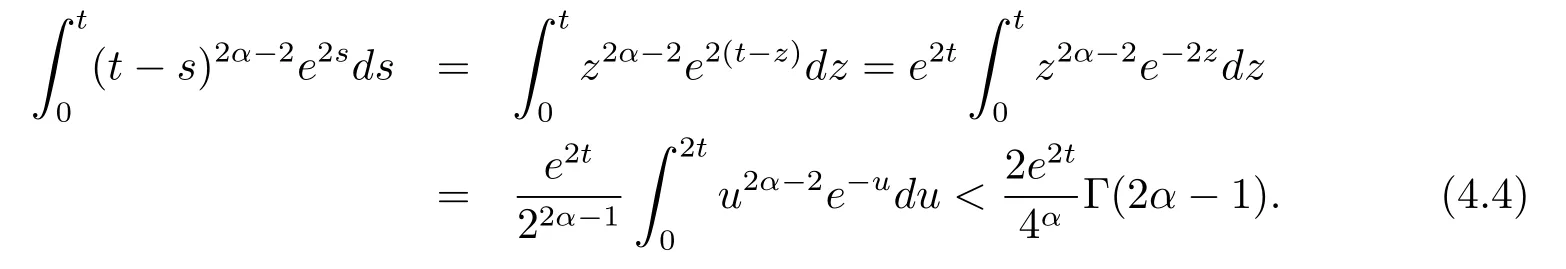
把(4.4)式带入(4.3)式,可得

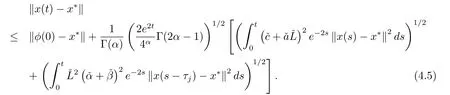
把引理2.3中λ=2和d=3应用到(4.5)式,可得

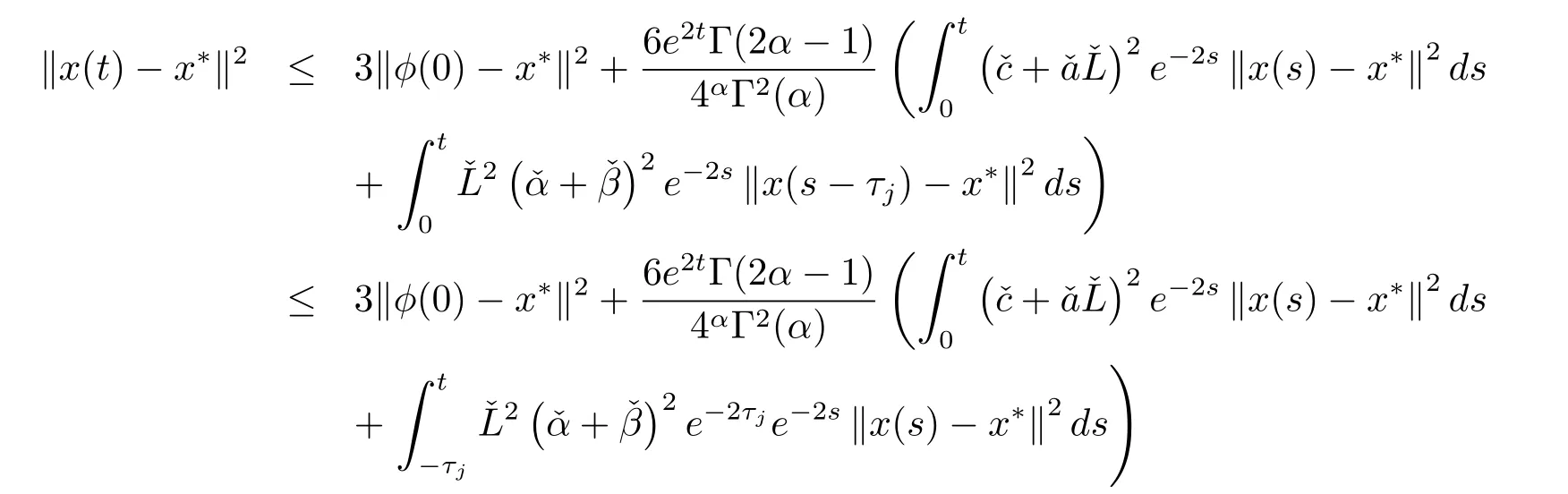
因为当t∈[-τ,0]时,有x(t)=φ(t),在结合范数‖|φ-x∗|‖=‖φ(t)-x∗‖,有

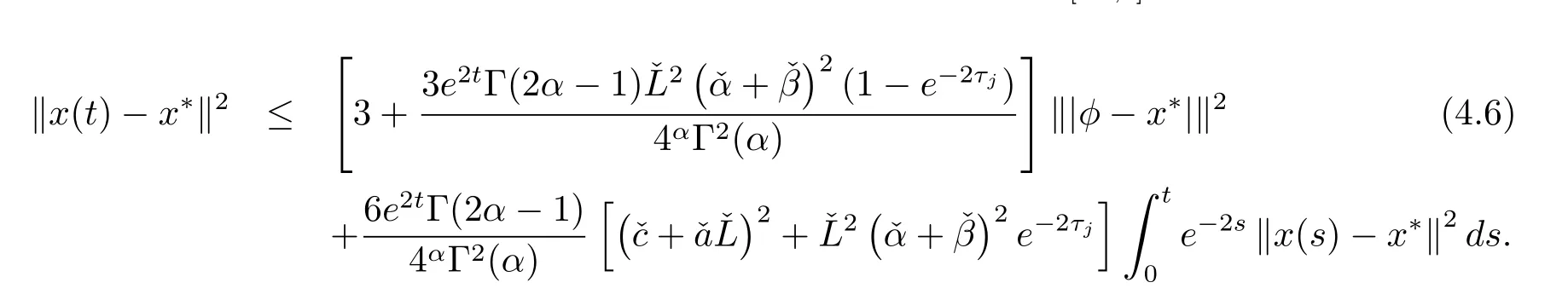
根据(4.6)式,可以有

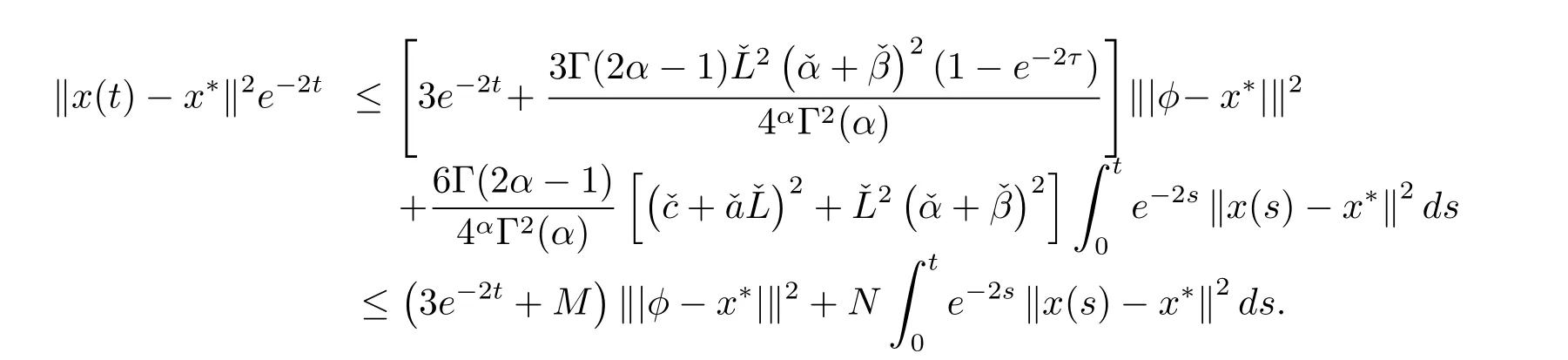
应用Gronwall不等式,可得

因此有

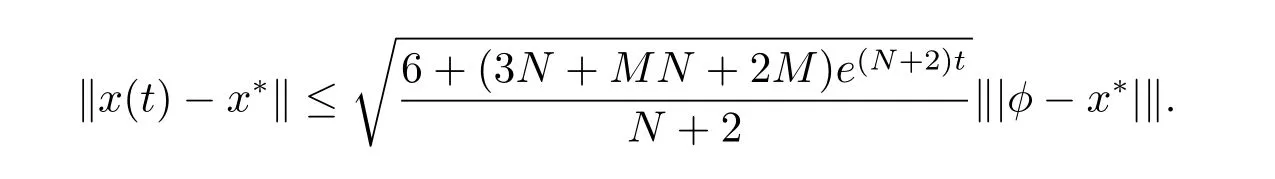
由此可知当‖|φ-x∗|‖＜δ时,并且(4.1)式成立,则‖x(t)-x∗‖＜ε.根据定义2.4,可知系统(1.1)中当0.5≤α＜1时平衡点x∗=()T关于{t0=0,δ,ε,T=[0,T],τ}是有限时间稳定.

定理4.2当0＜α＜0.5时,如果假设(H1)和(H2)成立,并且满足不等式

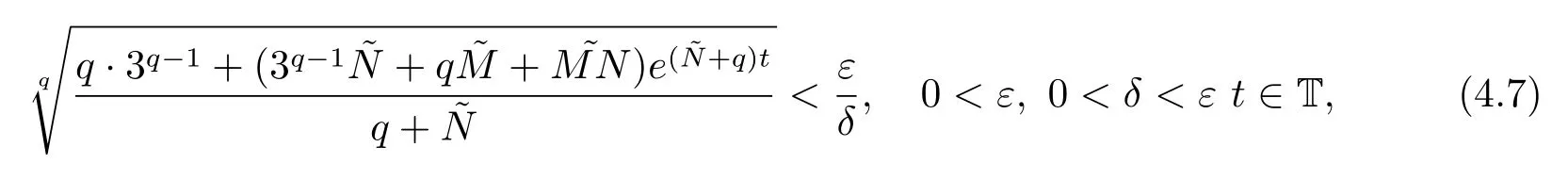
其中

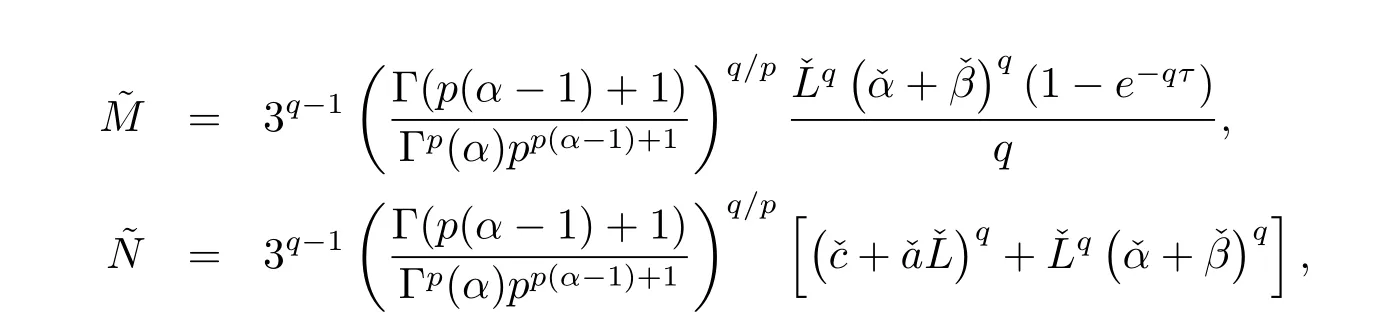
p=1+α,q=1+1/α,则系统(1.1)的唯一平衡点x∗=()T关于{t0= 0,δ,ε,T=[0,T],τ}是有限时间稳定.

证类似于定理4.1,对系统(1.1)有如下估计

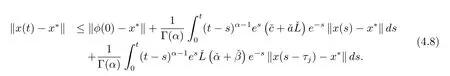
设p=1+α,q=1+1/α,显然,p,q＞1且1/p+1/q=1.利用Hder不等式,可得

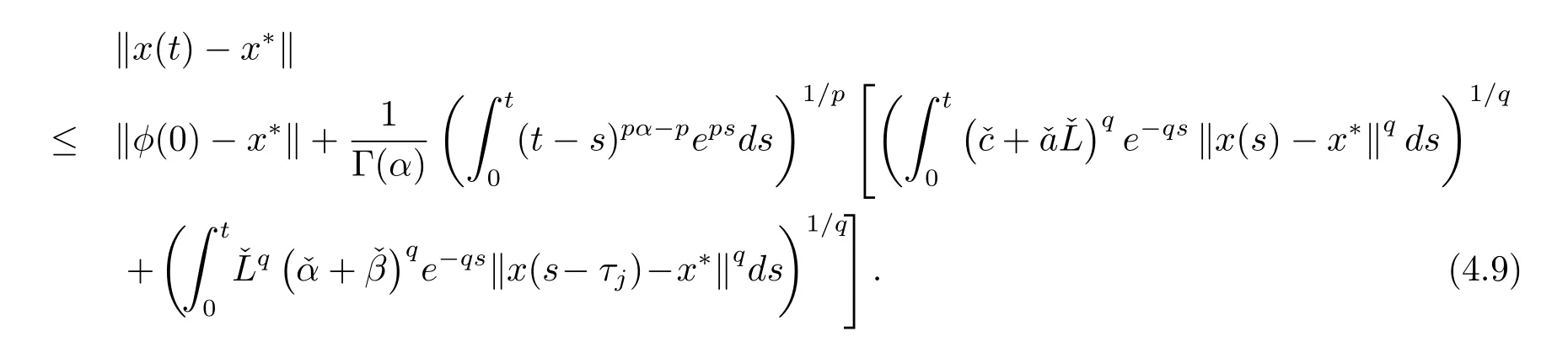
另一方面,有

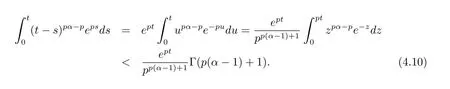
将(4.10)式代入(4.9)式,可得

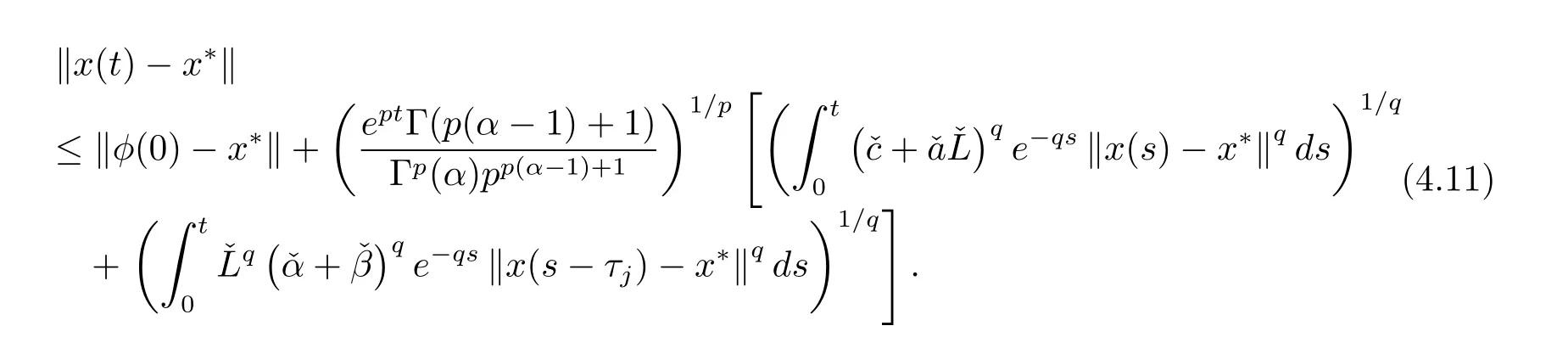
把引理2.3中λ=q和d=3应用到(4.11)式,可知

由此可得

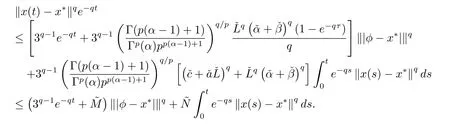
应用Gronwall不等式,可得

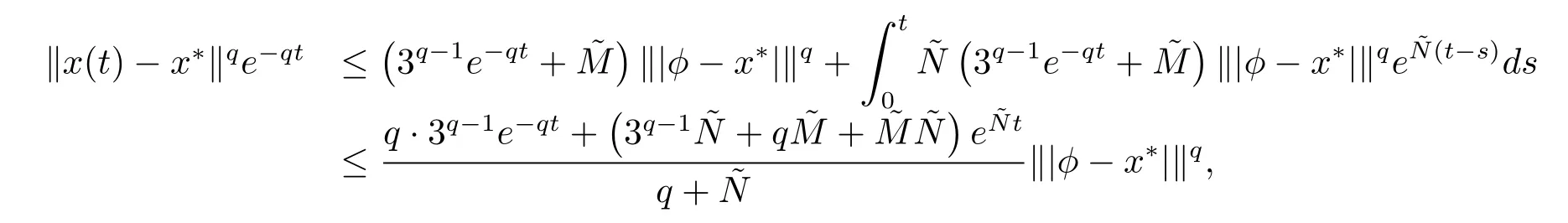
因此有

由此可知当‖|φ-x∗|‖＜δ且(4.7)式成立,则‖x(t)-x∗‖＜ε,根据定义2.4,可得出系统(1.1)中当0＜α＜0.5时平衡点x∗=()T关于{t0=0,δ,ε,T=[0,T],τ}是有限时间稳定.

5　数值仿真算法

因为大部分的分数阶微分方程不能求出解析解,所以在研究分数阶微分方程时,近似的数值方法是必要的.在文献[13]中,作者提出了一个数值算法(预估方法)求解分数阶微分方程.该方法是Adams-Bashforth-Moulton的方法的推广,考虑如下形式的分数阶微分方程

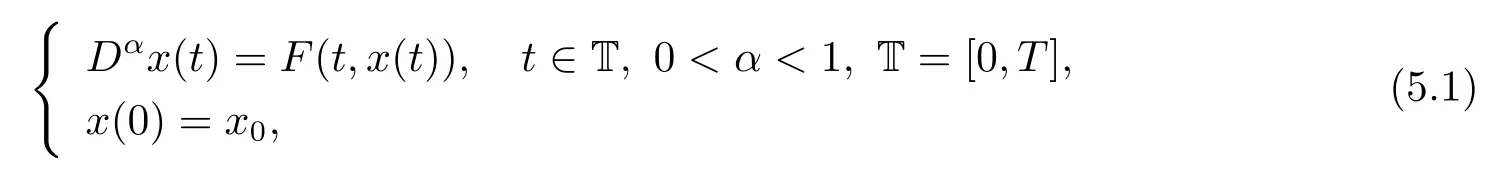
故方程(5.1)可以等价表示为

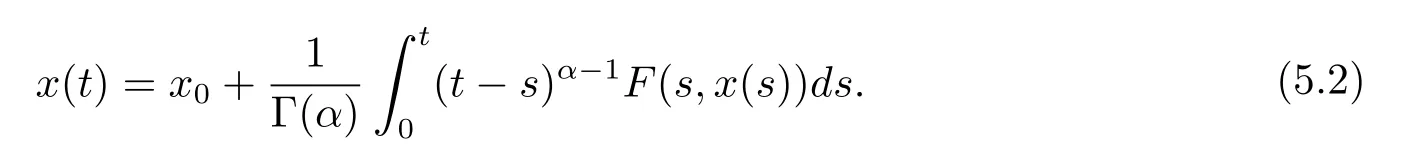
在本文中

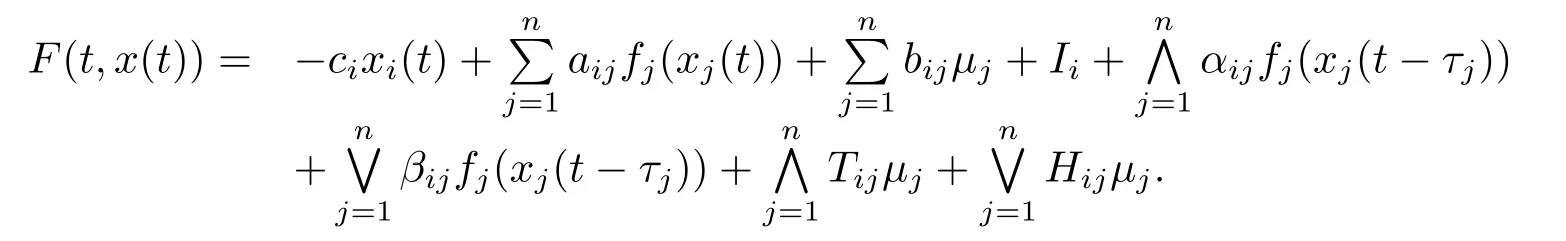
设h=T/N,tk=kh,k=0,1,2,···,N∈Z+,因此(5.2)式可写成

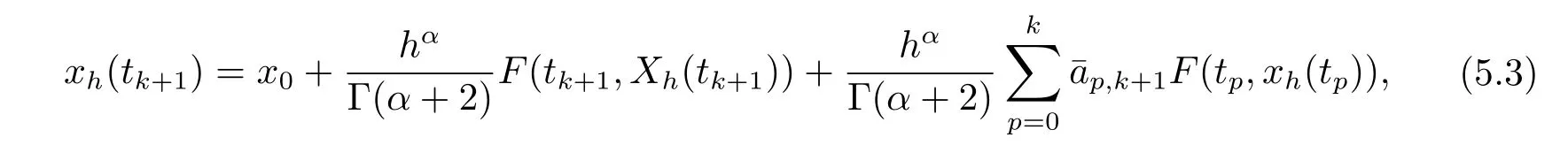
其中

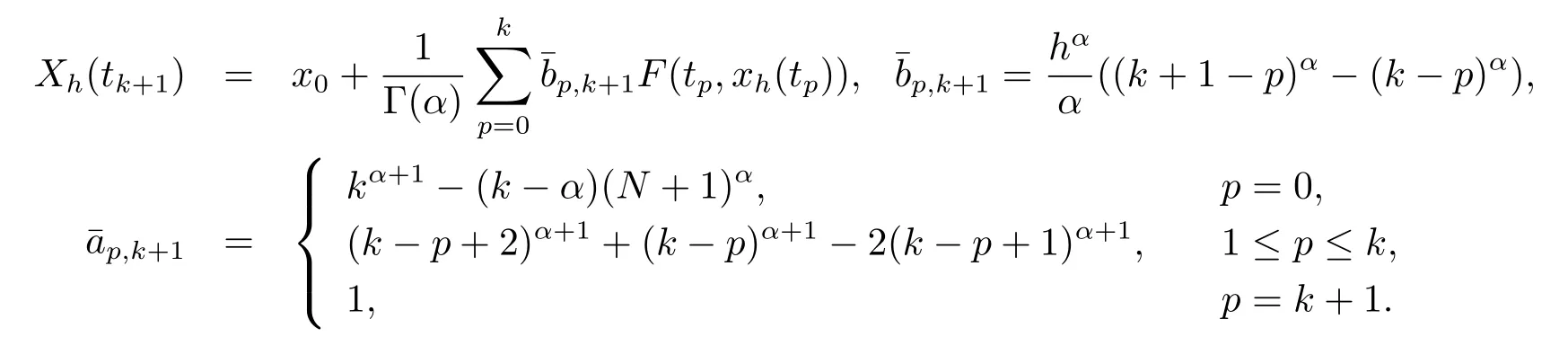
6　数值算例

本节将根据第5节的数值仿真算法,并通过一个数值算例来验证本文理论结果的正确性和有效性.

考虑如下带有变时滞的分数阶模糊神经网络模型:

图6.1当α=0.98和h=0.01时,分数阶模糊神经网络系统(6.1)的状态轨迹.

其中α=0.98,并且有c1=0.55,c2=0.45,a11=0.4,a12=-0.01,a21=0.01,a22=0.1, α11=-0.01,α12=-0.4,α21=-0.01,α22=-0.01,β11=0.01,β12=-0.01,β21=-0.1, β22=0.01,T11=0.02,T12=0.01,T21=-0.01,T22=0.05,H11=0.06,H12=0.01, H21=-0.01,H22=0.1,I1=-0.8,I2=0.3,µ1=µ2=0.1,τj=0.5,f2(x2(t))=x2(t)+1|+|x2(t)-1|),f1(x1)=tanh(x1).

显然,可以得出激活函数fj(xj(t))(j=1,2)满足假设条件(H1)并且可得Lj=1(j= 1,2).选取δ=0.036,ε=1,当α=0.98时,可以得到M=0.131887442012802,N= 1.839513983297748.从不等式

中可以估计出时间T=1.6137,在根据定理3.1和定理4.1可知,系统(6.1)有唯一的平衡点=(-2.98348,1.10785),并且关于{t0=0,δ=0.036,ε=1,T=[0,1.6137],τ=0.5}是有限时间稳定的.根据第5节的数值仿真,考虑如下情况.

情况1系统(6.1)的初始值为(x1,x2)=(-2.9816,1.1090).

情况3系统(6.1)的初始值为(x1,x2)=(-2.9854,1.1067).

根据图6.1知当时间步长h=0.01时,对于情况1-3可得出系统(6.1)的唯一平衡点是=(-2.98348,1.10785),并关于{t0=0,δ=0.036,ε=1,T=[0,1.6137],τ=0.5}是有限时间稳定的.说明了理论结果的正确性.

[1]Shu X B,Lai Y,Chen Y.The existence of mild solutions for impulsive fractional partial differentialequations[J].Nonl.Anal.TMA,2011,74:2003-2011.

[2]Li C P,Deng W H.Remarks on fractional derivatives[J].Appl.Math.Comput.,2007,187:777-784.

[3]Chen L P,Chai Y,Wu R C,Ma T D,Zhai H Z.Dynamic analysis of a class of fractional-order neural networks with delay[J].Neurocomputing,2013,11:190-194.

[4]蒋和平,蒋威.一类非线性分数阶泛函微分方程正解的存在性(英文)[J].数学杂志,2014,36(1):43-50.

[5]Chen J,Zeng Z,Jiang P.Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks[J].Neural Net.,2014,51:1-8.

[6]Yu J,Hu C,Jiang H.α-Stability and α-synchronization for fractional-order neural networks[J]. Neural Net.,2012,35:82-87.

[7]Li Y,Chen Y,Podlubny I.Stability of fractional-order nonlinear dynamic systems:Lyapunov direct method and generalized Mittag-Leffler stability[J].Comput.Math.Appl.,2010,59:1810-1821.

[8]Delavari H,Baleanu D,Sadati J.Stability analysis of Caputo fractional-order nonlinear systems revisited[J].Nonl.Dyn.,2012,67:2433-2439.

[9]Ke Y,Miao C.Stability analysis of fractional-order Cohen-Grossberg neural networks with time delay[J].Int.J.Comput.Math.,2015,92(6):1102-1113.

[10]刘可为,蒋威.分数阶中立型微分方程的有限时间稳定(英文)[J].数学杂志,2014,34(1):43-50.

[11]Yang L B,Wu C W,Chua L O.Fuzzy cellular neural networks:theory[J].Proc.IEEE Intern.Work. Cell.Neural Net.Appl.,1996:181-186.

[12]Kuczma M.An introduction to the theory of functional equations and inequalities:Cauchy’s equation and Jensen’s inequality[M].Basel:Birkhuser Verlag,2009.

[13]Diethelm K,Ford N J,Freed A D.A predictor-corrector approach for the numerical solution of fractional differential equations[J].Nonl.Dyn.,2002,29(1-4):3-22.

2010 MR Subject Classification:26A36;35R11;34D20;60H15

EXISTENCE,UNIQUENESS AND FINITE TIME STABILITY OF FRACTIONAL ORDER FUZZY NEURAL NETWORKS WITH DELAY

HA Jin-cai,YANG Hong-fu,ZHANG Qi-min
(School of Mathematics and Information Science,Beifang University for Nationalities, Yinchuan 750021,China)

In this paper,we introduce a class of fractional-order fuzzy neutral network system.According to Gronwall inequality,contraction mapping principle and the properties of fractional differential equation,the existence,uniqueness and finite time stability of fractional-order fuzzy neural networks with delay are researched.Finally,the numerical simulation is studied to illustrate the theory.

fractional-order fuzzy neutral network;existence;uniqueness;finite time stability

MR(2010)主题分类号:26A36;35R11;34D20;60H15O211.63

A

0255-7797(2016)06-1261-12

∗2015-07-03接收日期:2016-04-08

宁夏自然科学基金资助(NZ15104);国家自然科学基金资助(11461053;11261043);宁夏高校科研项目资助(NGY20140152).

哈金才(1971-),男,宁夏银川,副教授,研究方向:应用概率统计.

杨洪福.