平庸自旋体系的几何相位

刘凤敏，乔元新，于肇贤

(北京信息科技大学)



平庸自旋体系的几何相位

刘凤敏，乔元新，于肇贤

(北京信息科技大学)

利用不变量理论，研究了平庸自旋体系的几何相位.特别是在考虑到周期性变化的情况下，得到了的Aharonov-Anandan相位.

相位；自旋体系；不变量理论

众所周知，量子不变量理论是由 Lewis和 Riesenfeld在1969年首次提出的，它是处理与时间有关的哈密顿量系统的有力工具.通过引用基础不变量的概念和对于几何相(1984年Berry提出和1987年Aharonov等人提出)的研究，量子不变量理论在1991年被Gao等人广泛的参考，并且用于精确求解与时间有关的Schrödinger方程.Berry相位的提出不仅是对旧的量子绝热近似理论的突破，同时在更多的物理现象的研究中也提供了新的视角.

Berry相位的概念已经发展到了很多物理方向.该文利用不变量理论，将研究平庸自旋体系的动力学相位和几何相位.

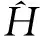
(1)

不变量|λn,n〉与时间有关的本征值方程为

(2)

(3)

|λn,t〉s=exp[iδn(t)]|λn,t〉

(4)

这表明，|λn,t〉s(n=1,2,…)是方程(3)式的一组完整的解.

Schrödinger方程(3)的通解可以写为

(5)

此时

(6)

Cn=〈λn,t|ψ(0)〉s.

考虑随时间变化的平庸自旋体系，它的哈密顿量形式如下

(7)

(8)

其对易关系为

(9)

令本量子体系的L-R不变量为

(10)

这里的θ和φ由方程(1)式决定，并且满足关系

(11)

Bzsinθcosθ=0

(12)

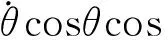
Bzsinθsinφ=0

(13)

其中，字母上方的点表示该字母对时间的导数.

可以构造幺正变换

(14)

容易得到

(15)

(16)

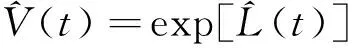
(17)

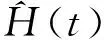
(18)

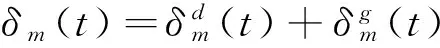
动力学相位为：

(19)

几何学相位为：

(20)

特别地，在考虑周期性变化的情况下，几何学相位变成如下形式：

(21)

这就是几何学Aharonov-Anandan相位.

综上，通过L-R不变量理论研究了平庸自旋体系的几何相位，分别表示出了动力学相位和几何学相位.特别地，当考虑周期性变化的情况下，给出了几何意义上的Aharonov-Anandan相位.

[1] Aharonov Y, Anandan J. Phase change during a cyclic quantum evolution[J]. Phys Rev Lett, 1987, 58(16):1953-1956.

[2] Berry M V. Quantal Phase Factors Accompanying Adiabatic Changes[J]. Proc R Soc A, 1984, 392(1802):45-47.

[3] Gao X C, Xu J B, Qian T Z. Geometric phase and the generalized invariant formulation[J]. Phys Rev A, 1992, 44(11):7016-7021.

[4] Lewis H R, Riesenfeld W B. An Exact quantum theory of the time dependent harmonic oscillator and of a charged particle time dependent electromagnetic field[J]. Math Phys, 1969, 10(8):1458-1473.

[5] Moody J, Shapere A, Wilczek F. Realizations of magnetic-monopole gauge fields: Diatoms and spin precession[J]. Phys Rev Lett, 1986, 56(9):893-896.

[6] Richardson D J, Kilvington A I, Green K, et al. Demonstration of Berry’s phase using stored ultra-cold neutrons[J]. Phys Rev Lett, 1988, 61(18):2030-2033.

[7] Sun C P, Ge M L. Generalizing Born-Oppenheimer approximations and observable effects of an induced gauge field[J]. Phys Rev D, 1990, 41(4):1349-1352.

[8] Sun C P. Quantum dynamical model for wave-function reduction in classical and macroscopic limits[J]. Phys Rev A, 1993, 48(2):898-906.

[9] Sun C P. Analytic treatment of high-order adiabatic approximations of twoneutrino oscillations in matter[J]. Phys Rev D, 1988, 38(9):2908-2910.

[10] Sun C P, et al. High-order quantum adiabatic approximation and Berry’s phase factor[J]. Phys A, 1988, 21(7):1595-1599.

[11] Wilczek F, Zee A. Appearance of Gauge Structure in Simple Dynamical Systems[J]. Phys Rev Lett, 1984, 52(24):2111-2114.

[12] Wei J, Norman E. Lie Algebraic Solution of Linear Differential Equations[J]. Math Phys, 1963, 4(4):575-581.Geometric Phase of Mediocre Spin System

(责任编辑：于达)

Liu Fengmin, Qiao Yuanxin，Yu Zhaoxian

(Beijing Information Science and Technology University)

Using the invariant theory, the geometric phase of the ordinary spin system is studied. Especially in the case of periodic variations, the Aharonov-Anandan phase is obtained.

Phase; Spin system; Invariant theory

2016-03-22

O413

A

1000-5617(2016)03-0022-02