分式布朗运动金融模型中的参数估计

毛小丽，孔凡胜，郭精军,b

（兰州财经大学a.统计学院；b.甘肃经济发展数量分析研究中心，兰州 730020）

分式布朗运动金融模型中的参数估计

毛小丽a，孔凡胜a，郭精军a,b

（兰州财经大学a.统计学院；b.甘肃经济发展数量分析研究中心，兰州 730020）

文章利用谱密度方法，分别研究金融中短期利率随机模型和股票价格随机模型。考虑短期利率随机模型—分式Ornstein-Uhlenbeck过程中漂移系数的极大似然估计问题，证明估计量的无偏性和渐近正态性，并用数值模拟实验验证估计方法的有效性。利用股票价格随机模型—分式几何布朗运动，选取平安银行2013年1月4日到2014年7月31日收盘价格数据，借助Monte Carlo方法进行模拟未来股票价格走势。研究表明：将分式布朗运动驱动的随机微分方程作为股票价格模型更能反映金融市场实际情况。

分式布朗运动；谱密度法；极大似然估计

0 引言

考虑如下第一类随机微分方程：

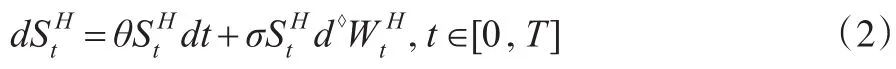
由于分式布朗运动驱动的Ornstein-Uhlenbeck（简称分式O-U过程）过程在物理、通信金融等领域有着广泛的应用，尤其分式O-U可以作为短期利率模型，故分式O-U过程的参数估计问题引起了众多学者的关注。Sottinen等［1］研究了带有附加分式布朗单的随机过程的参数估计，此估计基于分式布朗运动的Girsanor变换。同时，也可以用Euler-type方法对方程进行离散化处理后对未知参数进行估计。Hu等［2］用Malliavin计算，考虑了连续观测的分式O-U过程的极小平方估计及估计值的强一致性等。Xiao等［3］用极小对比估计方法，研究了分式O-U过程中未知参数的估计值。在文献［4，5］中用随机游走逼近分式布朗运动，然后用极大似然法估计漂移系数。同时，几何布朗运动是常见的描述股票价格未来走势的随机模型，该模型也是著名的Black-Scholes期权定价理论基础。张金清［6］用布朗运动模型对单风险因子和多风险因子进行了研究，并且在此基础上对Monte Carlo模拟法进行了改进与扩展，获得了许多有益的结论。郭精军等［7］利用分式布朗运动模型和Monte Carlo模拟法，以上证综指为例对金融市场风险进行了度量。

但是，上述估计方法一般需要随机分析中较为复杂和繁琐的计算才能得到参数估计值。本文拟采用另外一种比较直观的方法对分式高斯噪声进行逼近，已达到参数估计和股票价格趋势预测的目的。因为分式布朗运动的增量，即分式高斯噪声是一个平稳过程，所以可以用谱密度表示［9］的高斯过程来逼近分式高斯噪声。受到文献［6-8］的启发，本文利用谱密度方法对分式O-U过程中的漂移系数进行估计；进一步利用分式几何布朗运动来预测股票未来价格。最后，用数值实验分别验证估计值与真实值的差距以及股票价格预测准确程度。

1 分式布朗运动和相关结果

一个具有平稳增量的自相似过程WH={WH(t)，-∞＜t＜+∞}(其中Hurst参数0＜H＜1)称之为分式布朗运动,其均值为0,其协方差函数为：

考虑满足下列线性积分方程的高斯过程：

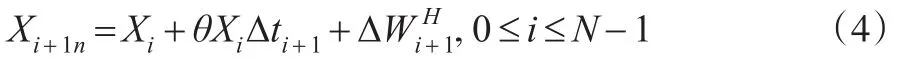
平稳离散型高斯过程X={Xn;n=0，…，N-1}可以表示为谱密度的积分形式：

这里等式表示方程两边有相同的分布,B1(λ)与B2(λ)是两个相互独立的布朗运动。

其中,ξi与ξj+1是独立同分布的标准正态随机变量,且文献[8]证明了:当l→∞，在L2下收敛于Xn。这里用代替ΔWH,仍然保持了最初过程的一些性质:自相似性、长相依性。

2 基于谱密度法的分式O-U过程参数估计

2.1 极大似然估计

利用文献[8]中的方法,现在通过极大似然法估计式(4)中的漂移系数θ,从i=0到i=j-1,对式(4)求和,有：

其中,B=( )

bk，l1≤k，l≤j是有下列元素的矩阵：(T表示转置),(Bξ)j表示向量Bξ的第j阶元素。通过乘以B-1,得到：

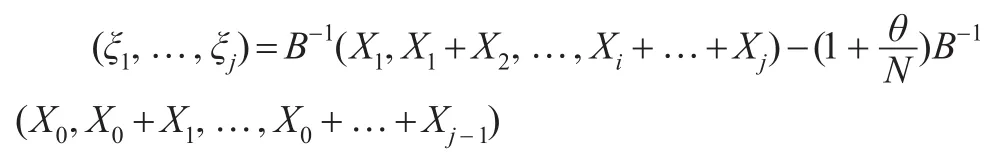
因此,对于每一个 j≥1,ξj由观测 X1，…，Xj可表示为：

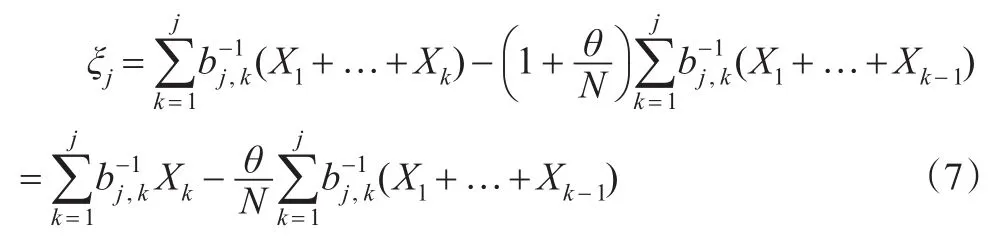
下面给出模型(4)中未知参数的极大似然估计的表达式。

定理1：模型(4)中θ的极大似然估计为：

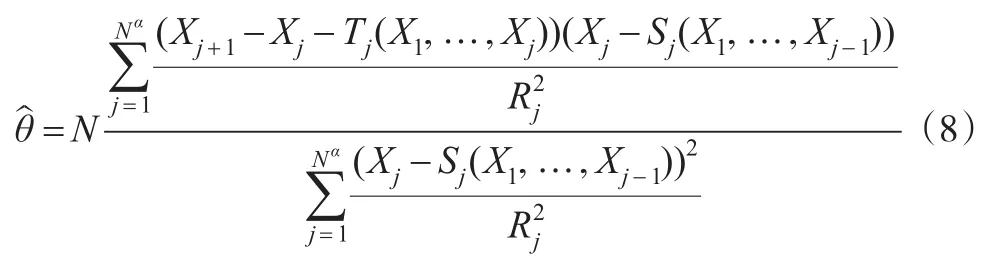
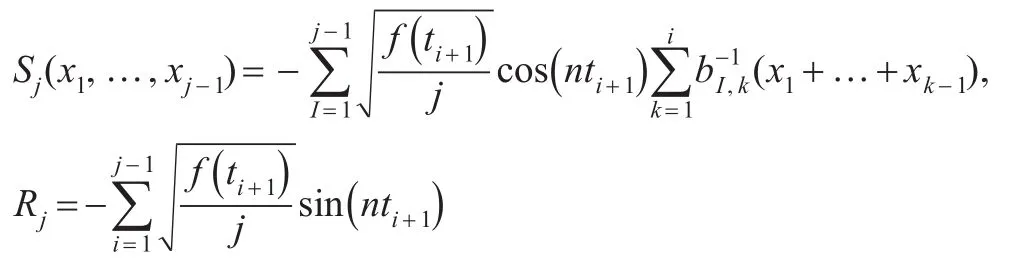
因此,在X1=x1,…,Xj=xj的条件下,Xj-1的条件期望是高斯分布其中：

其概率密度函数为：

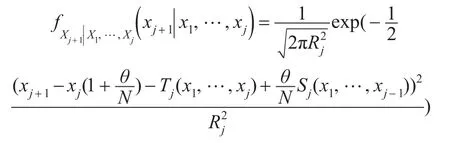
故似然函数为：

因此,将参数θ的似然函数L(θ，，x1，…，xNα)极大化,得到θ的极大似然估计θ∧为：

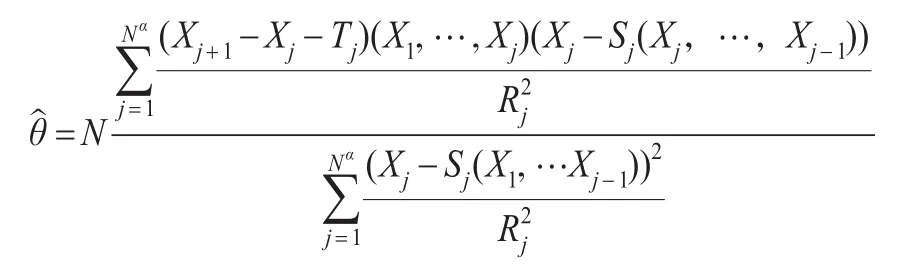
证毕。

从θ的极大似然估计θ∧和式(9),得到：

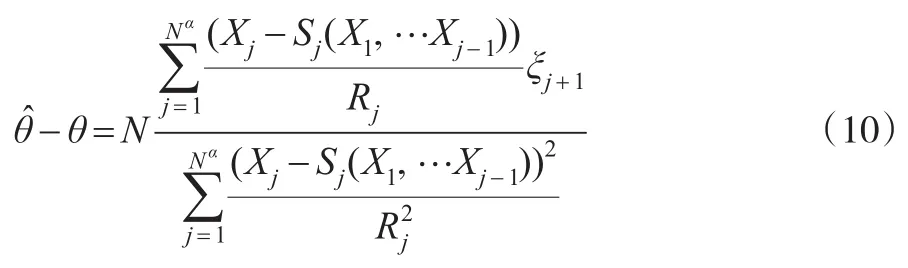
2.2 估计量的性质

现在证明估计量的无偏性、渐近正态性。

对M≥1,定义：

证明：从式(10)、式(11)和式(12),得到：

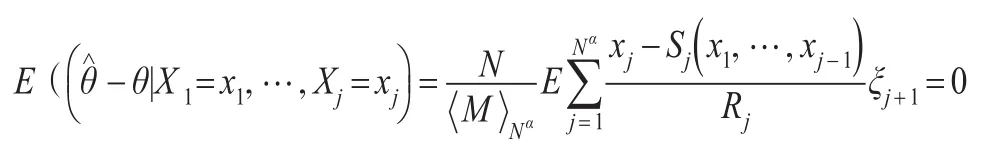
命题2：从式（10）得到：

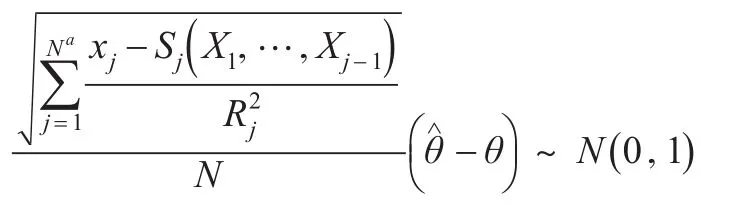
这是由于 ξj+1是独立同分布的正态随机变量。

2.3 Monte Carlo模拟

选取平安银行2013年1月4日到2014年7月31日收盘价格数据，对得到的估计量进行模拟。取不同的H和θ，根据模型（3），利用R代码产生300个样本，从而求出估计量的均值和标准差（如表1所示）。

表1 估计量的均值和标准差

从模拟结果看到，对于取的不同的H和θ，通过模型（3）模拟后得出的估计量的均值都接近真实值，并且对应于不同的H和θ模拟的估计量的标准差也比较小，通过模拟可以发现，在对样本量不太大的情况进行模拟时，模拟得出的估计量相对来说也是比较精确的。

3 谱密度法在股票价格模型中的应用

3.1 随机标准法下的股票价格预测

考虑下列的方程：

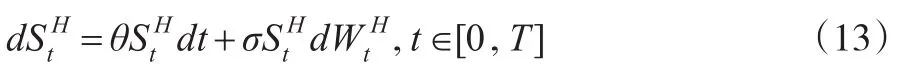
其中，n=1，2，...，N;B1是b+1维独立同分布的标准正态随机向量；B2是N+1维独立同分布的标准正态随机向量；B1和B2相互独立；CH是一个常数。取文献中已证明是WH(t)的一个好的逼近。

于是，利用式（14）得到式（13）的离散化形式：

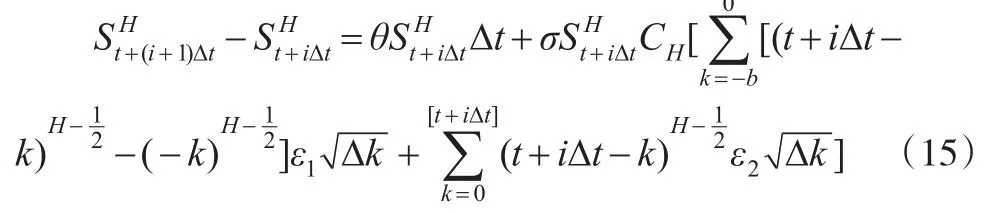
其中ε1和ε2都是均值为0、方差为1的标准正态随机变量，[t+iΔt]表示对t+iΔt进行取整。

步骤二：用平安银行2013年1月1日到2014年7月31日收盘价格估计出参数。

步骤三：利用计算机生成b+1、N+1个相互独立的标准正态随机变量，不妨记为{ε1i∶i=1，2，...，b+1}和{ε2j∶j=1，2，...，N+1}，代入离散化表达式（15）中。

步骤四：令初始值i=0，通过编程，由初始平安银行股票价格得到再由生成依次递推，直到于是，在二维平面上绘的散点图，就得到到期日平安银行股票价格未来变化的一条模拟样本轨道。

3.2 谱密度法下的股票价格预测

用谱密度法对式（13）进行离散化处理，类似地可以模拟股票价格，具体步骤如下：

步骤一：利用式（6）得到式（13）的离散化形式：

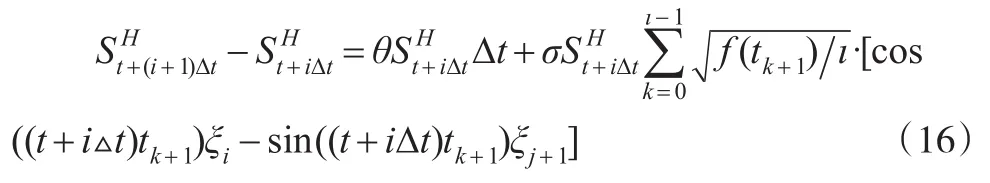
步骤二：利用计算机生成ι个相互独立的标准正态随机变量，不妨记为和代入离散化表达式（16）中。

步骤三：令初始值i=0，通过R语言编程，由初始平安银行股票价格得到，再由生成依次递推，直到于是，在二维平面可绘出集合{(t的散点图，从而得到分式布朗运动方程（13）的一条近似样本轨道，即该股票价格的一条模拟样本轨道。

3.3 比较分析

在用随机标准法和谱密度法模拟平安银行股票价格的变化路径时，通过计算得到H=0.75，θ=-0.001266，σ=0.02，初始价格St=10.70。在随机标准法的随机模型中，取CH=1，t=0，Δt=Δk=1，在谱密度法的随机模型中，取t=0，Δt=1，n=123，得到图1和图2所示的平安银行股票价格的一条样本轨道，并与股票价格的实际走势进行对比。

图1 随机标准法模拟股价走势与实际走势对比图

图2 谱密度法模拟股价走势与实际走势对比图

图中粗线是平安银行2014年8月1日到2015年1月30日实际收盘价（数据来源：Wind资讯），细线是模拟的价格。

通过对比发现，谱密度法估计的分式布朗运动模型比随机标准法估计的随机模型更贴近实际，但与实际还有点差距，造成这种差距的原因是：程序中有产生随机数的过程，具有很大的随机性；模型中只对股价进行了量化分析，事实上影响股票价格的因素除了数量因素外，还有政策、投资者心理等因素。

4 结论

鉴于分式布朗运动具有良好的长相依性、自相似性等特征，本文主要用谱密度方法和分式布朗运动金融模型，对短期利率模型进行极大似然估计，数值实验说明该估计方法比较准确；结合Monte Carlo模拟方法，最大限度地模拟出股票价格未来走势，模拟结果不受历史数据的影响，且模拟的结果更加贴近于现实。

[1]Sottinen T,Tudor C.Parameter Estimation for Stochastic Equations With Additive Fractional Brownian Sheet[J].Statis.Infere.Stoch.Pro⁃cess,2008,（11）.

[2]Hu Y,Nualart D.Parameter Estimation for Fractional Ornstein-Uhlen⁃beck Process[J].Stat.Prob.Lett.,2010,80.

[3]Xiao W,Zhang W,Zhang X.Minimum Contrast Estimator for Frac⁃tional Ornstein-uhlenbeck Process[J].Science China Mathematics, 2012,55(7).

[4]Bertin K,Torres S,Tudor C.Drift Parameter Estimation in Fraction⁃al Diffusions,Martingales and Random Walks[J].Stat.Prob.Lett., 2011,81(2).

[5]Bertin K,Torres S,Tudor C.Maximum Likelihood Estimators and Random Walks in Long-memory Models[J].Statistics,2010,44(5).

[6]张金清.金融风险管理(第二版）[M].上海:复旦大学出版社,2011.

[7]郭精军,田婧.分式布朗运动模型下的金融市场风险度量——以上证指数为例[J].兰州商学院学报,2014,30(2).

[8]LauraR,SoledadT,TudorC.ComparativeEstimationforDiscreteFrac⁃tional Ornstein-uhlenbeck Process[J].StochasticModels,2014,29(3).

[9]Ton D.Simulation of Fractional Brownian Motion[J].Prbability in the Engineering&Information Sciences,2004,2.

[10]Hu Y,Wang X.Exact Maximum Likelihood Estimator for Drift Frac⁃tional Brownian Motion at Discrete Observation[J].Acta Mathemati⁃ca Scientia,2011,31B(5).

[11]Sottinen T.Fractional Brownian Motion,Random Walks and Binary Market Models[J].Finance and Stochastics,2011,（5）.

（责任编辑/易永生）

O211.6

A

1002-6487（2016）23-0025-04

国家自然科学基金资助项目（71561017）；甘肃省自然科学基金资助项目（145RJZA033）；甘肃经济发展数量分析研究中心项目（SLYB201202）

毛小丽（1989—），女，甘肃临洮人，硕士研究生，研究方向：应用数理统计。

孔凡胜（1990—），男，山东兖州人，硕士研究生，研究方向：应用数理统计。

（通讯作者）郭精军（1976—），男，甘肃民勤人，博士，副教授，研究方向：应用数理统计、随机分析。