离散时间系统响应求解及其待定系数确定

张玲霞， 宋代宁， 齐会云

(西安电子科技大学 空间科学与技术学院， 陕西 西安 710071)

离散时间系统响应求解及其待定系数确定

张玲霞， 宋代宁， 齐会云

(西安电子科技大学 空间科学与技术学院， 陕西 西安 710071)

响应求解是“信号与系统”课程教学中的核心内容。离散时间系统中方程右边有激励的移位序列的线性组合时，求解零状态响应的常用方法都是激励分解法，但最后结果形式复杂，难以化简和分析。本文提出一种直接求解及确定待定系数的方法。与激励分解法相比，该方法结果表示简单，计算方便，既可以计算零状态响应，也可以计算全响应。

离散时间系统；经典解；响应；初始条件

0 引言

离散时间系统的时域分析是“信号与系统”课程中的重要部分，其实质就是求解给定初始条件下的差分方程。与连续时间系统的微分方程不同，离散时间系统的差分方程具有迭代性，不同响应的初始条件之间可以相互转换，不用像连续系统那样，需要采用冲激平衡法判定初值是否跳变，这为离散时间系统的分析带来方便，而且响应计算结果的表示也更为多样和灵活[1]。经典求解方法将全解分为齐次解和特解，特解中的待定系数由原方程直接确定，齐次解中的待定系数由全解的初始条件确定。在遇到方程右边出现激励的移位序列或移位序列的线性组合时，大多教材的讲解都是基于激励分解的思想[1-7]：先将激励分解为简单激励或其移位的线性组合，再对简单激励引起的响应求解，然后再根据线性时不变系统的特点，按照分解激励的组合形式将其对应的响应也进行相应的线性组合。这样处理其物理意义明确，初值迭代量也小，但是结果繁琐，难以验证和后续分析，而且只是针对零状态响应。教材[8-10]讨论了单位序列响应的一种直接求解方法，对确定待定系数的初始条件的选取均有涉及，但是没有给出初始条件选取的最简规则。

由于二阶常系数的差分方程的求解是教材中的经典题型，本文以二阶离散系统为例，给出一种求解具有多移位序列激励系统响应的方法和待定系数确定方法，并给出证明，不用分解激励，计算过程简单，结果表示清晰明了，不仅可以计算全响应，也可以计算零状态响应。

1 问题的提出

某线性时不变系统方程为：y(k)+3y(k-1)+2y(k-2)=f(k)-0.5f(k-1)，当f(k)=ε(k)+2ε(k-1)时，求该系统的零状态响应yzx(k)。

解： (激励分解法)将激励f(k)=ε(k)+2ε(k-1)代入方程，有

yzs(k)+3yzs(k-1)+2yzs(k-2)=ε(k)+1.5ε(k-1)-ε(k-2)

(1)

方程右边是ε(k)及其移位序列的线性组合，引入辅助变量y1(k)(简单激励ε(k)引起的响应)，有

(2)

只要计算出简单激励ε(k)的零状态响应y1zs(k)，则yzs(k)可以由下式的线性组合表示：

yzs(k)=y1zs(k)+1.5y1zs(k-1)-y1zs(k-2)

(3)

因此，问题的关键就是根据式(2)计算出y1zs(k)了。

y1zs(k)+3y1zs(k-1)+2y1zs(k-2)=1,k≥0

(4)

由式(2)迭代计算初值y1zs(0)=1,y1zs(1)=-2，则由经典解法，可设：

(5)

代初值y1zs(0)=1,y1zs(1)=-2，得C1=-1/2,C2=4/3，则

(6)

最后，由式(3)得：

(7)

此结果表示形式复杂，难以化简和验证。本文给出一种直接方法。

2 本文提出的方法(直接求解法)

由式(1)进行迭代，计算初值：yzs(0)=1，yzs(1)=-2,yzs(2)=1,yzs(3)=-0.5当k≥2时，式(1)变为

yzs(k)+3yzs(k-1)+2yzs(k-2)=1.5

(8)

由经典解法，设

yzs(k)=C1(-1)k+C2(-2)k+0.25,k≥2

(9)

观察式(9)，为求待定系数C1,C2，需要代初值yzs(2),yzs(3)，则

(10)

得C1=0.75,C2=0，则

yzs(k)=[0.75(-1)k+0.25]ε(k-2)

(11)

补充k=0,k=1时刻的初值，有

yzs(k)=[0.75(-1)k+0.25]ε(k-2)+δ(k)-0.5δ(k-1)

(12)

实际上，可以证明，C1,C2的求解可以直接代k≥2的前两个时刻的初值yzs(0)和yzs(1)，结果与式(10)计算的相同。但结果表示更为简单，见下式：

yzs(k)=[0.75(-1)k+0.25]ε(k)

(13)

3 推广应用

假设系统方程为：y(k)+a1y(k-1)+a2y(k-2)=b0f(k)+b1f(k-1)+b2f(k-2) ，且已知激励

f(k)=skε(k)，y(-1),y(-2)也为已知，求y(k)。

求解思路：

(1)迭代计算初值yzs(0)y0，y(1)y1。

(2)求解，当k≥2时，方程为

y(k)+a1y(k-1)+a1y(k-2)=b0sk+b1sk-1+b2sk-2

(14)

由经典解法，设

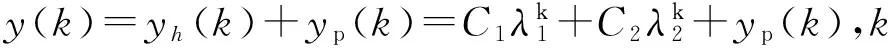
(15)

特解系数可以由式(14)计算。代入y(0),y(1)初值，确定待定系数，代入式(14)，有

(16)

如果初值y(-1)，y(-2)均为零，则此响应为零状态响应，式(16)可以表示为

(17)

由以上求解过程可知，式(15)中的待定系数C1和C2，应由初值y(2)和y(3)确定，但用初值y(0)和y(1)求解的C1和C2也是相同的，而且响应表示更简单。下面给出证明。第一种情况：特征单根λ1≠λ2且s不等于特征根

设特解yp(k)=Psk，k≥2，代入式(14)，得

(18)

则式(15)为

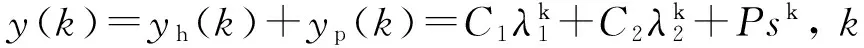
(19)

迭代计算初值yzs(0)y0,y(1)y1

y(2)=b0s2+b1s+b2-a1y1-a2y0=m-a1y1-a2y0

(20)

y(3)=b0s3+b1s2+b2s-a1y2-a2y1=ms-a1m+

(21)

其中：m=b0s2-b1s+b2，结合式(18)，有

m=b0s2+b1s+b2=P(s2+a1s+a2)

(22)

将初值y(2)和y(3)代入式(19)，有

(23)

推出待定系数

(24)

式中：A=(Ps2λ2-Ps3+a1a2y0+λ2a2y0)，

B=(Ps2λ1-Ps3+a1a2y0+λ1a2y0)

将C1和C2代入式(19)，即可得全响应y(k)，但此式不包含y(0)和y(1)。若直接代k=2的前两个时刻的初值y(0)和y(1)，有

(25)

得

(26)

则全响应为

(27)

即要证明

(28)

(29)

首先证明式(28)成立，式(29)由λ1与λ2的对称性易证。

由特征方程及维达定理：

(30)

以及式(22)，可以推出式(28)左边分子中

[A+m(s-a1-λ2)]

=(Ps2λ2-Ps3-λ1a2y0)+m(s+λ1)

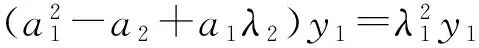
第二种情况：s等于一特征单根，不妨设s=λ1≠λ2

可计算出特解为yp(k)=(P1k+P0)sk,k≥2，其中

(31)

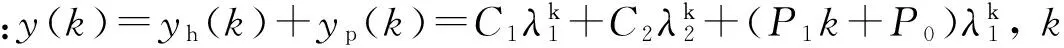
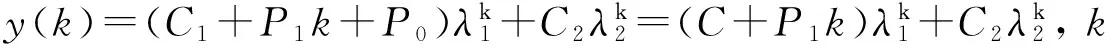
(32)

其中C=C1+P0。

将初值y(2),y(3)代入式(32)，确定待定系数，得

(33)

其中：

m=b0s2+b1s+b2=-P1(a1λ1+2a2)

(34)

(35)

则全响应为

(36)

如果直接代k=2的前两个时刻的初值y(0)和y(1)，有

(37)

得

(38)

代入式(36)，全响应为

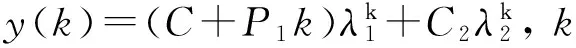
(39)

由式(30)及式(34)，很容易推出

C2=

C=

第三种情况：s等于特征重根，即s=λ1=λ2=λ

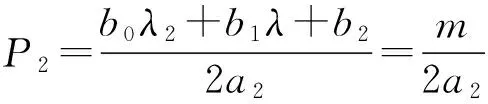
m=b0s2+b1s+b2=2a2P2

(40)

设y(k)=yh(k)+yp(k)=(C1k+C2)λk+(P2k2+P1k+P0)λk，k≥2，即

y(k)=(C1k+C2+P2k2+P1k+P0)λk=(P2k2+Pk+C)λk,k≥2

(41)

其中P=C1+P1,C=C2+P0。

将初值y(2),y(3)代入式(41)，确定待定系数，得

(42)

式(30)变为λ2+a1λ+a2=0及λ=-2a1,λ2=a2，求解得

(43)

此时，响应为

y(k)=(P2k2+P0k+C)λk,k≥2

(44)

如果直接代k=2的前两个时刻的初值y(0)和y(1)，有

(45)

得

(46)

则响应

y(k)=(P2k2+P0k+C)λk,k≥0

(47)

4 小结

(1)直接使用初值y(0)和y(1)计算待定系数，不仅省去迭代y(2)和y(3)的麻烦，而且结果更为简单。若式(14)中b2或b1为零，也可用初值y(0)和y(1)确定待定系数。

(2)上述证明过程与y(-1)和y(-2)的具体数值无关，说明本文方法不仅可以用于全响应的求解，也适用于零状态响应的求解。采用激励分解法求解零状态响应时，需要引入辅助变量，辅助变量的零状态响应初值均为0。而辅助变量的全响应初值不一定为零。因此，教材中讲解的激励分解法只适用于零状态响应的求解，不适合全响应的计算。

(3)直观理解k≥m(m=0,1,2)的全解的结构中已经包含了k≥m的激励信息，而k≥m的两个初值y(m)和y(m+1)是由k

(张玲霞等文)

因此直接代入k

(4)本文所述方法也可以直接计算单位序列响应h(k)，例如，

h(k)+3h(k-1)+2h(k-2)=δ(k)-0.5δ(k-2)

当k≥3时,

h(k)+3h(k-1)+2h(k-2)=0

其解h(k)=C1(-1)k+C2(-2)k,k≥3中直接代时刻k=3之前的初值h(1)和h(2)计算待定系数即可，此时h(k)可表示为h(k)=[C1(-1)k+C2(-2)k]ε(k-1)+h(0)δ(k)

当单位序列响应方程为h(k)+3h(k-1)+2h(k-2)=δ(k)时，其解h(k)=C1(-1)k+C2(-2)k,k≥1中直接代k=1的前两个初值h(-1)和h(0)即可，此时h(k)可表示为

h(k)=[C1(-1)k+C2(-2)k]ε(k)。

5 结语

离散时间系统的响应求解是“信号与系统”课程中的主要内容之一，其结果表示灵活多样，在用经典解法求解时，其初始条件可由方程迭代计算，非常简单。但是如果初始条件选取不当，响应的表示会很复杂，难以验证和化简。本文探讨一种计算过程简单，结果表示清晰明了的响应求解方法，特别是当系统方程中出现激励的移位序列或移位序列的线性组合时，该方法的优势更为明显。该方法不仅适用于零状态响应求解，也适用于全响应求解。本文只对激励为指数型的因果序列f(k)=skε(k)进行了证明，对于其它幂函数或三角函数形式的激励未加考虑，有待于继续完善。

[1] 吴大正，信号与线性系统分析(第4版)[M]， 北京：高等教育出版社，2005.8.

[2] 徐亚宁，苏启常，信号与系统(第三版)[M]，北京：电子工业出版社，2011.7.

[3] 曾黄麟，信号与线性系统[M]，北京：科学出版社，2011.2

[4] 金波，张正炳，信号与系统分析[M]，北京：高等教育出版社，2011.4.[5] 邓翔宇，信号与系统(第二版)[M]，北京：清华大学出版社，北京交通大学出版社，2005.7

[6] 张永瑞，信号与系统(精编版)[M]，西安：西安电子科技大学出版社，2014.6.

[7] 张晔，信号与系统[M]，哈尔滨：哈尔滨工业大学出版社，2010.12. [8] 郭宝龙，闫允一，朱娟娟等，工程信号与系统[M]，北京：高等教育出版社，2014.7.

[9] 吕幼新，张明友编著，信号与系统(第二版)[M]，北京：电子工业出版社，2007.8.

[10] 陈后金，胡健，薛健，信号与系统(第二版)[M]，北京：清华大学出版社，北京交通大学出版社，2005.7

Method to Solve the Response and Its Undetermined Coefficients of LTI Discrete System

ZHANG Ling-xia, SONG Dai-ning, QI Hui-yun

(SchoolofAerospaceScience&Technology,XidianUniversity,Xi'an710071，China)

The response analysis of linear time-invariant (LTI) system is the core of the Signal and System course. The solving zero-state response is commonly based on the decomposition of the excitation when the excitation is a linear combination of simple signal and its sequences. But the final results are complex in the form and difficult to simplify and subsequent analysis. In this paper, a method to determine the response and its undetermined coefficients is given. Compared with excitation decomposition, the presented method is simple, convenient and can be used to compute zero-state response or complete response.

discrete-time system; classical solution; response; initial condition

2015-06-25;

2015-09- 23

张玲霞(1965-)，女，博士，副教授，主要从事电路、信号课程教学以及综合测试与故障诊断等科研工作，E-mail: zlxnpu@163.com

G420

A

1008-0686(2016)02-0067-05