探究一类直线与圆综合问题的求解根源

◇ 江苏 王治刚



探究一类直线与圆综合问题的求解根源

◇ 江苏 王治刚

直线与圆综合问题常以直线和圆的位置关系(相切、相交、相离)为命题视角,求解中只要准确把握二者位置关系的判定条件(圆心到直线的距离与半径之间的大小关系),即可以不变应万变．

图1

例1已知圆O:x2+y2=1,若直线y=kx+2上总存在点P,使得过点P的圆O的2条切线互相垂直,则实数k的取值范围是________.

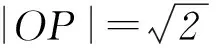
k2≥1,k∈(-∞,-1]∪[1,+∞)．

下面就此类问题的相关变式拓展探究．

1 变换已知,由明确到隐含

例2直线l:3x+4y+a=0,圆C:(x-2)2+y2=2,若在圆C上存在2点P、Q,在直线l上存在点M,使得∠PMQ=90°,则a的取值范围是( ).

分析本题与例1相比,并没有直接说明MP、MQ为切线,但根据图形之间的位置关系,不难发现只需考查MP、MQ与圆C相切且满足∠PMQ=90°时的情况即可.

2 逆向探究,确定点的位置

例3已知圆C:x2+y2=2,直线l:x+2y-4=0,点P(x0,y0)在直线l上,若存在圆C上的点Q,使得∠OPQ=45°(O为坐标原点),则x0的取值范围是( ).

分析本题与例2相比,直线方程已知,问题转化为探究点P的位置,因此可从以下2种视角实现问题的解答．

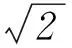
故正确选项为B.

图2

3 改变结论,变定角为动角

例4已知P为直线y=x+1上的一动点,过P作圆C:(x-3)2+y2=1的切线PA、PB,A、B为切点, 则当|PC|=________时,∠APB最大．

图3

分析本题改变例1的求解结论,求角∠APB取得最大值的条件,即在三角形中求解角度的最值问题,把求∠APB的最大值转化为求∠APC的最大值．在三角形中,可以利用三角形的边角关系把问题转化为求“圆心到直线的最短距离”．

解如图3，由圆的切线性质知

∠APB=2∠APC.

4 变换条件,改变夹角大小

图4

分析本题将例1中∠APB=90°改为60°,可借助例4的方法求解．

解如图4所示，由圆的切线性质可知∠APO=∠BPO=30°,且OA⊥PA.

在Rt△AOP中,

|PO|=2|OA|=2．

上述问题虽然问法不同,但解题的方法都是将问题转化为直线与圆的位置关系,因此我们要善于在“变”中求“不变”,利用我们所学的基础知识、解题规律和思想方法进行探究.

著名的数学教育家波利亚曾形象的指出:“好问题同某种蘑菇有些相像,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个．”学习中由一个基本问题出发,运用改变条件、改变结论、改变形式、改变求解方法等,探索问题的发展变化,使我们发现问题的本质．变中求进、进中求通,拓展创新空间,引导学生的思维向纵深拓展．

江苏省徐州市第三十六中学)