关于点集拓扑课程中若干易混淆概念的分析
李 静,李红杰
(周口师范学院 数学与统计学院,河南 周口 466001)
关于点集拓扑课程中若干易混淆概念的分析
李 静,李红杰
(周口师范学院 数学与统计学院,河南 周口 466001)
点集拓扑学是本科阶段的一门专业课程,由于它逻辑性强,内容抽象,学习起来相当困难.根据多年来对点集拓扑的教学经验总结,针对学生易混淆或难理解的概念,给出学习这些概念时应注意的事项,并借助具体例子进行分析讲解,使初学者能更好地掌握这些概念.
点集拓扑;度量空间;拓扑空间;关系;开集;连续映射
0 引言
在各种数学分支中接触到的最基本的概念,比如极限、距离(度量)、连续、边界、路径等,都源于拓扑.点集拓扑是一门由一系列抽象概念构成的学科,它的定理、推论、性质等都是在概念的基础上展开而获得的.在教材里,每一章每一节都有新概念出现,并且这些概念都环环相扣,如果有一些概念理解不透,将影响后面概念的理解.因此,在教学中要融会贯通,把这些概念和以前学过的基本概念比较记忆,在教学中给出一些具体的实例,使学生对新概念能有更清晰的认识.
1 关系
定义1[1]设有集合X和Y,集合
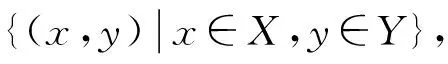
称为X与Y的笛卡儿积,记作X×Y.
注1 给定两个集合,通过取它们的笛卡儿积以得到一个新的集合,这种做法我们并不陌生.以前通过实数集合构造复数集合,通过直线构造平面时,用的就是这种方法.
注2 我们用于有序偶的记号和用于“开区间”的记号是一样的,有时容易混淆.
定义2[1]设X,Y是两个集合.如果R是X与Y的笛卡儿积X×Y的一个子集,即R⊂X×Y,则称R是从X到Y的一个关系.
对于初学者来讲,关系的定义有点难以理解,因为它与我们平时所理解的关系有很大区别,针对关系的定义我们给出以下几点注意事项:
注3 关系是一种集合.
注4 任一有序偶的集合确定了一个二元关系.
注5 函数(映射)、等价、序、运算等概念都是关系的特例;尤其是映射要求像唯一,关系没要求,函数要求定义域与值域是数域,而映射不一定.

2 有标集族及其并和交
定义3[1]设Γ是一个集合.如果对于每一个γ∈Γ,指定了一个集合A,我们就说给定了一个有标集族{Aγ}γ∈Γ,或者在不至于引起混淆的情形下说给定了一个集族{Aγ}γ∈Γ,其中Γ称为(有标)集族{Aγ}γ∈Γ的指标集.
定义4[1]设给定了一个集族{Aγ}γ∈Γ,集合
称为集族{Aγ}γ∈Γ的并集或并,记作∪γ∈ΓAγ; 当指标集Γ非空时,集合
称为集族{Aγ}γ∈Γ的交集或交,记作∩γ∈ΓAγ.
注6 在以往集族的并与交计算时,有些同学把计算结果理解成了集族,而根据定义集族的并与交的结果是集合.
例2 设Γ={1,2,3},A1={a},A2={a,b},A3={c,d},则{Aγ}γ∈Γ是一个有标集族.
例3 设Γ={1,2,3},A1={a,b},A2={a,c},A3={a,d},求∪γ∈ΓAγ及∩γ∈ΓAγ.
解 根据集族并集和交集的定义得
∪γ∈ΓAγ={a,b,c,d},
∩γ∈ΓAγ={a}.
3 离散的度量空间与离散空间
定义5 设(X,ρ)是一个度量空间.称(X,ρ)是离散的,或者称ρ是X的一个离散度量,如果对于每一个x∈X,存在一个实数δx>0使得ρ(x,y)>δx对于任何y∈X,y≠x成立.
例4 假定X是一个集合,定义ρ:X×X→R使得对于任何x,y∈X,有

容易验证是ρ是X的一个离散度量,因此度量空间(X,ρ)是离散的.
定义6 设有集合X,若令T=P(X),也就是X的子集全体所构成的族,那么易证T是X的一个拓扑,并称之为X的离散拓扑;同时把拓扑空间(X,T)称为一个离散空间.在离散空间(X,T)中,X的任意一个子集都是开集.
例5 设X={a,b},令T={Φ,X,{a},{b}},则T是X的离散拓扑,(X,T)是离散空间.
注7 大家常常把这两个定义弄混淆,离散的度量空间是一种度量空间,它的本质和关键是度量[2],而离散空间是一种拓扑空间,它的本质和关键是拓扑.同时它们之间也有一些联系,每一个只含有限个点的度量空间是离散的度量空间,这样的一个度量空间作为拓扑空间也是离散空间 .这样,我们就抓住了它们的本质,弄清楚它们之间的联系与区别,从而很容易区分这两个概念.
4 开集
在学习初等数学时,我们都学习开区间 (a,b).这是定义在一维空间上的或者说定义在直线上的,怎么推广到二维空间,或者更高维空间上呢?最直观的想法,就是“一个不包含边界的集合”.可是,给一个集合,怎么定义它的“边界”?在拓扑学里面,开集是最基本的概念,它是定义在集合运算的基础上的.它要求开集符合这样的条件:开集的任意并集和有限交集仍为开集.下面我们看一下开集在拓扑学中的定义.
定义7 设度量空间(X,ρ),x∈X.对任何实数ε>0,集合
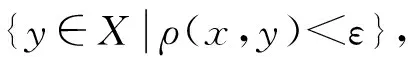
记作B(x,ε),称为以x为中心、以ε为半径的球形邻域.
定义8 设A是度量空间X的一个子集.如果A中的每一个点都有一个球形邻域包含于A(即对于每一个a∈A,存在实数ε>0使得B(a,ε)⊂A),则称A是度量空间X中的一个开集.
注8 此处的开集仅是度量空间的开集.
定义9[1]设X是一个集合,T是X的一个子集族,如果T满足以下条件:
1)X,∅∈T;
2)若A,B∈T,则A∩B∈T;
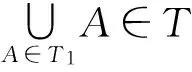
那么就称T是X的一个拓扑.若T是X的一个拓扑,则称(X,T)是一个拓扑空间,T里面的每一个元素都称为拓扑空间(X,T)中的一个开集.
注9 此处的开集是拓扑空间的开集.拓扑空间中的开集虽然定义简单,但有些学生最初对这样的定义方式百思不解,不过,经过后面的学习,发现这样的定义有着重要的意义:保证了开集中每个点都有一个邻域包含在这个集合内,所有点都和外界(补集)保持距离.这样的理解比使用集合运算的定义有更清晰的几何意义.但是,直观的事物不容易直接形成严谨的定义,使用集合运算则更为严格.而集合运算定义中,任意并集的封闭性是对这个几何特点的内在保证.因此,我们学习定义的时候一定要认真,掌握准确.
注10 条件2)蕴涵着:有限多个开集的交仍是开集,条件3)蕴涵着:任意多个开集的并仍是开集.
例6 平庸空间.设X是一个集合,令T={X,∅},容易验证T是X的一个拓扑,称之为X的平庸拓扑;并且我们称拓扑空间(X,T)为一个平庸空间.在平庸空间中,有且只有两个开集,即X本身和∅.
5 可度量化空间
定义10 设(X,ρ)是一个度量空间,令Tρ为由X中的所有开集构成的集族,(X,Tρ)是X的一个拓扑,称Tρ为X的由度量ρ诱导出来的拓扑.
定义11 设(X,T)是一个拓扑空间.如果存在X的一个度量ρ使得拓扑T即是由度量ρ诱导出来的拓扑Tρ,则称(X,T)是一个可度量化空间.
例7 设X={1,2},T={X,∅},(X,T)是平庸拓扑空间,这里诱导拓扑Tρ={∅,X,{1},{2}},显然Tρ≠T,因此,(X,T)不是可度量化的.
注11 由此例可见,一个平庸空间如果含有多于一个点的话,它肯定不是离散空间,那么它不是可度量化的.因此,不是每一个拓扑空间的拓扑都可以由某一个度量诱导出来,或者说拓扑空间比可度量空间的范围要广泛.
6 邻域
定义12 设x是度量空间X中的一个点,U是X的一个子集.如果存在一个开集V满足条件:x∈V⊂U,则称是U点x的一个邻域.
注12 这里的开集指度量空间中的开集,邻域指度量空间中的邻域.
定义13 若(X,T)是一个拓扑空间,x∈X.如果X的一个子集U满足以下条件:存在一个开集V∈T使得x∈V⊂U,那么我们就说U是点x的一个邻域.点x的邻域系,指的是x的所有邻域构成X的子集族.
注13 这里的开集指拓扑空间中的开集,邻域指拓扑空间中的邻域.当我们把一个度量空间看作拓扑空间时(这时,空间的拓扑是由度量诱导出来的拓扑),一个集合是不是某一个点的邻域,无论是按定义12或者是按定义13,都是一回事.
例8 设X={1,2,3},令T={Φ,X,{1}},试写出点1的所有邻域.
解 因为
1∈{1}⊂{1},1∈{1}⊂{1,2},1∈{1}⊂{1,3},1∈{1}⊂X或1∈X⊂X,
所以点1的邻域有{1},{1,2},{1,3},X.
7 连续映射
在学习微积分时,一个耳熟能详的连续函数的定义,最直观的意思就是“足够近的点保证映射到任意小的范围内”,可是,这种定义依赖于实数空间,不在实数空间的映射又怎么办呢?拓扑的定义是“如果一个映射的值域中任何开集的原像都是开集,那么它连续”,这样就与实数空间没有关系了.下面我们看一下度量空间和拓扑空间中映射整体连续和在某一点连续的定义.
定义14 设度量空间X和Y,f:X→Y,且x0∈X.若对f(x0)的任意球形邻域B(f(x0),ε),存在x0的某一球形邻域B(x0,δ),使得
f(B(x0,δ))⊂B(f(x0),ε),
则称映射在点x0处是连续的.
如果映射f在X的每一个点x∈X处连续,则称f是一个连续映射.
注14 以上先给出度量空间映射在某一点连续的定义,再给出映射整体连续的定义,实质上是数学分析中函数连续性定义的纯粹形式推广.因为如果设ρ和ρ1分别是度量空间X和Y中的度量,则f在点x0处连续可以说成:对于任意给定的实数ε>0,存在实数δ>0使得对于任何x∈X,只要ρ(x,x0)<δ(即x∈B(x0,δ)),便有ρ1(f(x),f(x0))<ε(即f(x)∈B(f(x0),ε)).
数学分析中所讨论的空间是n维欧氏空间[3],欧氏空间是度量空间的一个特例,将欧氏空间再推广即得到拓扑空间.因此,拓扑学所讨论的问题有许多与数学分析中的相关问题是平行的,它们之间既有联系又有区别.
下面将度量空间之间的连续映射概念推广为拓扑空间之间的连续映射.
定义15 设两个拓扑空间X和Y,f:X→Y,若Y中的每一个开集U的原像f-1(U)是X中的一个开集,则称f是从X到Y的一个连续映射.
注15 当X和Y是两个度量空间时,如果f:X→Y是从度量空间X到度量空间Y的一个连续映射,那么它也是拓扑空间X到拓扑空间Y的一个连续映射;反之亦然(这里涉及的拓扑指诱导拓扑).
在拓扑空间中,我们是先建立邻域的概念,然后再给出映射在某点连续性的概念.下面我们将度量空间之间的连续映射在一点连续性的概念推广到拓扑空间之间的映射中.
定义16 设X和Y是两个拓扑空间,f:X→Y,x∈X.如果f(x)∈Y的每一个邻域U的原像f-1(U)是x∈X的一个邻域,则称映射f是一个在点x处连续的映射.
注16 当X和Y是两个度量空间时,如果f:X→Y是从度量空间X到度量空间Y的一个映射,它在某一点x∈X处连续,那么它也是拓扑空间X到拓扑空间Y的一个在点x处连续的映射;反之亦然.
8 小结
总之,点集拓扑学概念都是从学生熟知的概念进一步拓展和抽象出来的,准确地掌握住新的概念,是学好点集拓扑的关键[4].如何上好点集拓扑概念课,是教学过程中值得深入研究的问题,我们只是略微探讨,但仍有许多好的教学方法有待于我们进一步讨论.
[1]熊金城.点集拓扑讲义[M].4版.北京:高等教育出版社,2011:11-66.
[2]王其林,廖正琦.点集拓扑教学中提高学生的抽象思维能力探讨[J].重庆文理学院学报,2009,28(6):79-81.
[3]夏大峰.点集拓扑教学方法的几点讨论[J].阜阳师范学院学报,2002,19(2):42-47.
[4]田亚.《点集拓扑》课程教学的新认识与实践[J].邢台学院学报,2012,27(2):166-167.
Analysis on Some Confusing Concepts in Course of Point Set Topology
LI Jing,LI Hongjie
(SchoolofMathematicsandStatistics,ZhoukouNormalUniversity,Zhoukou466001,China)
Point set topology is a professional course in undergraduate phase.Due to its logic and abstract content,learning it is quite difficult.According to many years teaching experience of point set topology,the attentions are given for students to understand the confusing or difficult concepts in their learning.By the analysis on specific examples,help beginners better grasp of these concepts.
point set topology; metric space; topological space; relationship; open set; continuous map
2016-08-18
河南省高等学校重点科研项目(16A110026)
李 静(1986—),女,河南周口人,周口师范学院数学与统计学院教师.
10.3969/j.issn.1007-0834.2016.04.016
G642.0;O189.1
1007-0834(2016)04-0064-04

