非连通图2D3，4∪G的优美标号

吴跃生

（华东交通大学理学院，江西南昌330013）

非连通图2D3，4∪G的优美标号

吴跃生

（华东交通大学理学院，江西南昌330013）

讨论了非连通图2D3，4∪G的优美性，给出了非连通图D3，4∪G是优美图的二十一个充分条件.证明了非连通图2D3，4∪G(k)+a（a=2，3，4，5，6，8，9，…，23）都是优美的.

优美图；交错图；非连通图；优美标号

引言

记号[m，n]表示整数集合{m，m＋1，…，n}，m和n均为非负整数，且满足0≤m＜n.记号G(k)+m表示图G是特征为k且缺k＋m标号值的交错图.本文所讨论的图均为无向简单图，记号V（G）和E（G）分别表示图G的顶点集和边集，未说明的符号及术语均同文献[1-17].

图的优美标号问题是组合数学中一个热门课题[1-17].

1 概念

定义1[1]对于一个图G=（V，E），称G是优美图，θ是G的一组优美标号是指：如果存在一个单射使得对所有边e=uv∈E（G），由导出的映射是一个双射.

定义2[2]设θ是图G的优美标号，V（G）=X∪Y，且X∪Y=Φ，如果，则称θ是G的交错标号.称G是在交错标号θ下的交错图.称k为交错图G关于交错标号θ的特征.

把任意m个圈Cn的恰有一个公共点所组成的图记作Dm，n[1].

非连通图2D3，4存在特征为12，且缺6，14，15，22和23标号值的交错标号，如图1所示，为方便记，把如图1所示的标号记为：（13；9，21，10；12，19，11；8，17，7）；（24；3，16，2；0，18，1；4，20，5）；

非连通图2D3，4存在特征为11，且缺1，2，9，10和18标号值的交错标号，如图2所示，为方便记，把如图2所示的标号记为：（11；15，3，4；12，5，13；16，7，17）；（0；21，8，22；24，6，23；20，4，19）；本文讨论了非连通图2D3，4∪G的优美性.

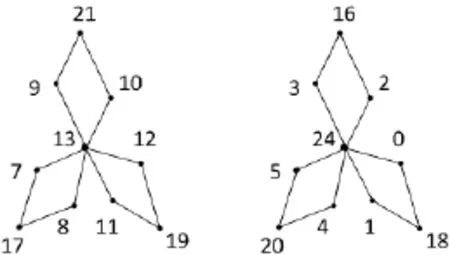
图1 非连通图2D3，4的交错标号

图2 非连通图2D3，4的交错标号

2 主要结果及其证明

（1）特征为k＋14且缺k＋1，k＋8，k＋16，k＋17和k＋20标号值的交错标号；

（2）特征为k＋14且缺k＋1，k＋8，k＋16，k＋17和k＋24标号值的交错标号.

证设2D3，4如图2所示，设X，Y是图G(k)＋2的一个二分化，θ1是图G(k)＋2的交错标号，且

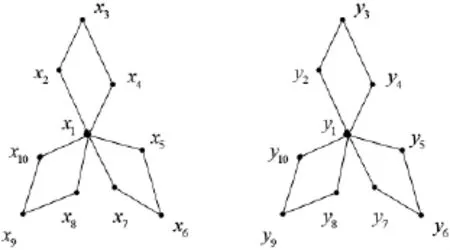
图3 非连通图2D3，4

非连通图2D3，4∪G(k)+2的各种顶点标号θ定义为：

第一种标号：θ（x1）=k＋15，θ（x2）=k＋12，θ（x3）=k＋23，θ（x4）=k＋11，θ（x5）=k＋14，θ（x6）=k＋21，θ（x7）=k＋13，θ（x8）=k＋10，θ（x9）=k＋19，θ（x10）=k＋9，简记为（下文同）：（k＋15；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）.

θ（y1）=k＋24，θ（y2）=k＋5，θ（y3）=k＋18，θ（y4）=k＋4，θ（y5）=k＋3，θ（y6）=k＋26，θ（y7）=k＋2，θ（y8）=k＋7，θ（y9）=k＋22，θ（y10）=k＋6.简记为（下文同）：

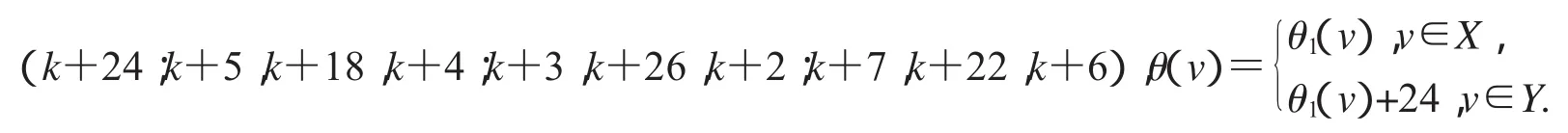
第二种标号：（k＋15；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）；

下面证明第一种标号θ是非连通图2D3，4∪G(k)＋2的优美标号.

（1）θ：X→[0，k]是单射；θ：Y→[k＋25，q＋24]－{k＋26}是单射；

θ：V（2D3，4）→[k＋2，k＋24]∪{k＋26}－{k＋8，k＋16，k＋17，k＋20}是双射；

有θ：V（2D3，4∪G(k)+2）→[0，q＋24]－{k＋1，k＋8，k＋16，k＋17，k＋20}是单射.

θ'：E（2D3，4）→[1，24]是双射；

θ'：E（G(k)＋2）→[25，q＋24]是双射.

θ'：E（2D3，4∪G(k)＋2）→[1，q＋24]是一一对应.

由（1）和（2）可知第一种标号θ就是非连通图2D3，4∪G(k)+2的缺k＋1，k＋8，k＋16，k＋17和k＋20标号值的优美标号.

令X1=X∪{x2，x4，x5，x7，x8，x10}∪{y2，y4，y5，y7，y8，y10}，

Y1=Y∪{x1，x3，x6，x9}∪{y1，y3，y6，y9}，

所以，第一种标号θ就是非连通图D2，4∪G(k)＋2的特征为k＋14，且缺k＋1，k＋8，k＋16，k＋17和k＋20标号值的交错标号.

其他各种标号的证明可仿上.证毕.

以下定理只给出标号，定理证明与定理1的第一种标号证明过程类似，故省略.

设2D3，4如图2所示，设X，Y是图G(k)＋3的一个二分化，θ1是图G(k)＋3的交错标号，且

非连通图2D3，4∪G(k)＋3的顶点标号θ定义为：

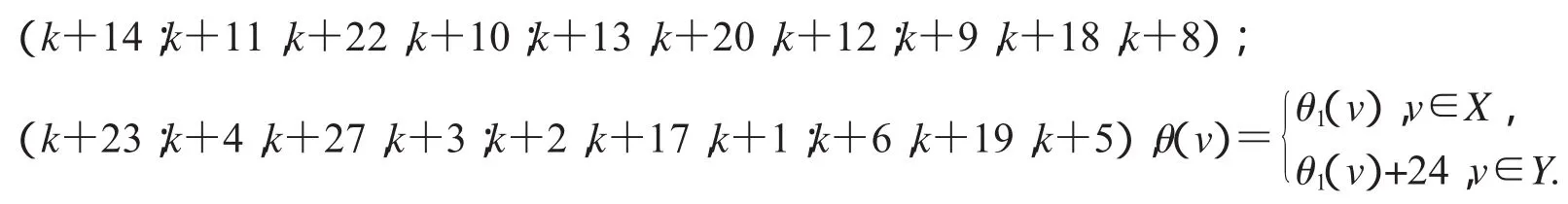
设2D3，4如图2所示，设X，Y是图G(k)＋4的一个二分化，θ1是图G(k)＋4的交错标号，且

非连通图2D3，4∪G(k)＋4的顶点标号θ定义为：

设2D3，4如图2所示，设X，Y是图G(k)＋5的一个二分化，θ1是图G(k)＋5的交错标号，且

非连通图2D3，4∪G(k)＋5的顶点标号θ定义为：

设2D3，4如图2所示，设X，Y是图G(k)＋6的一个二分化，θ1是图G(k)＋6的交错标号，且

非连通图2D3，4∪G(k)＋6的顶点标号θ定义为：

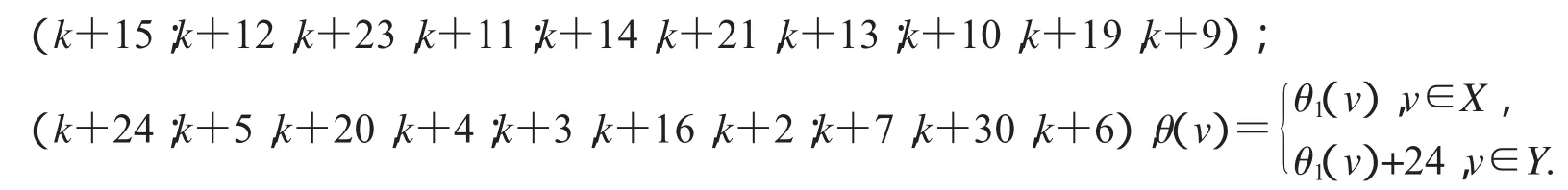
（1）特征为k＋13且缺k＋7，k＋16，k＋20，k＋21和k＋24标号值的交错标号；

（2）缺k＋14，k＋15，k＋16，k＋23和k＋24标号值的交错标号.

设2D3，4如图2所示，设X，Y是图G(k)＋8的一个二分化，θ1是图G(k)＋8的交错标号，且

非连通图2D3，4∪G(k)＋8的各种顶点标号θ定义为：

第一种标号为：（k＋14；k＋11，k＋18，k＋10；k＋13，k＋22，k＋12；k＋9，k＋32，k＋8）；

第二种标号为：（k＋32；k＋11，k＋22，k＋10；k＋13，k＋20，k＋12；k＋9，k＋18，k＋8）；

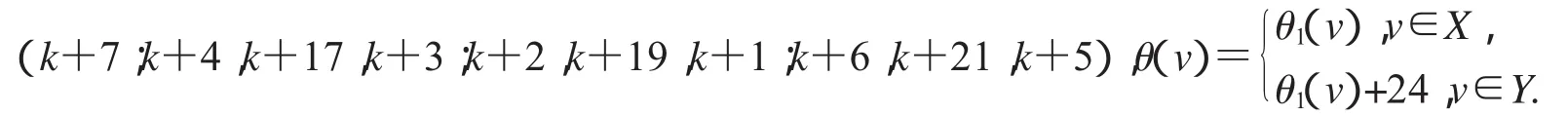
（1）特征为k＋14且缺k＋1，k＋8，k＋17，k＋21和k＋22标号值的交错标号.

（2）缺k＋1，k＋15，k＋16，k＋17和k＋24标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋9的一个二分化，θ1是图G(k)＋9的交错标号，且

非连通图2D3，4∪G(k)＋9的各种顶点标号θ定义为：

第一种标号为：（k＋15；k＋12，k＋19，k＋11；k＋14，k＋23，k＋13；k＋10，k＋33，k＋9）；

第二种标号为：（k＋33；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）；

（1）特征为k＋13且缺k＋7，k＋16，k＋21，k＋22和k＋24标号值的交错标号；

（2）缺k＋1，k＋2，k＋16，k＋17和k＋18标号值的优美标号；

（3）缺k＋7，k＋8，k＋9，k＋23和k＋24标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋10的一个二分化，θ1是图G(k)＋10的交错标号，且

非连通图2D3，4∪G(k)＋10的各种顶点标号θ定义为：

第一种标号为：（k＋14；k＋11，k＋34，k＋10；k＋13，k＋20，k＋12；k＋9，k＋18，k＋8）；

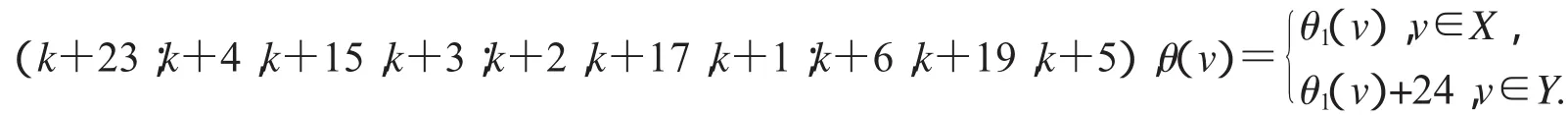
第二种标号为：（k＋34；k＋13，k＋24，k＋12；k＋15，k＋22，k＋14；k＋11，k＋20，k＋10）；

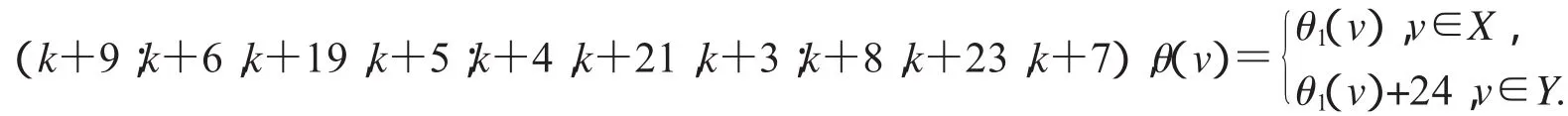
第三种标号为：（k＋34；k＋13，k＋1，k＋12；k＋11，k＋3，k＋10；k＋15，k＋5，k＋14），

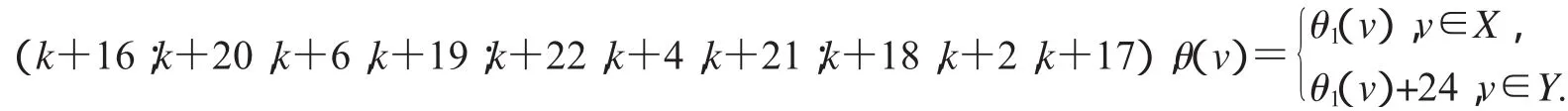
（1）特征为k＋14且缺k＋1，k＋8，k＋17，k＋22和k＋23标号值的交错标号；

（2）缺k＋2，k＋3，k＋6，k＋17和k＋24标号值的优美标号；

（3）缺k＋1，k＋8，k＋9，k＋10和k＋24标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋11的一个二分化，θ1是图G(k)＋11的交错标号，且

非连通图2D3，4∪G(k)＋11的各种顶点标号θ定义为：

第一种标号为：（k＋15；k＋12，k＋35，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9），

第二种标号为：（k＋10；k＋14，k＋4，k＋13；k＋12，k＋35，k＋11；k＋16，k＋8，k＋15），

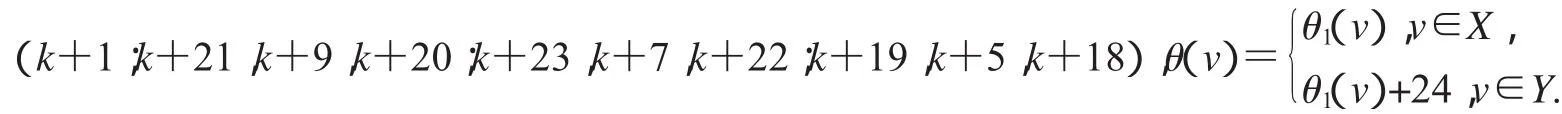
第三种标号为：（k＋35；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

（1）特征为k＋13且缺k＋7，k＋18，k＋21，k＋22和k＋24标号值的交错标号；

（2）缺k＋1，k＋3，k＋4，k＋7和k＋18标号值的优美标号；

（3）缺k＋1，k＋2，k＋9，k＋10和k＋11标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋12的一个二分化，θ1是图G(k)＋12的交错标号，且

非连通图2D3，4∪G(k)＋12的各种顶点标号θ定义为：

第一种标号为：（k＋14；k＋11，k＋20，k＋10；k＋13，k＋36，k＋12；k＋9，k＋16，k＋8），

第二种标号为：（k＋11；k＋15，k＋5，k＋14；k＋13，k＋36，k＋12；k＋17，k＋9，k＋16），

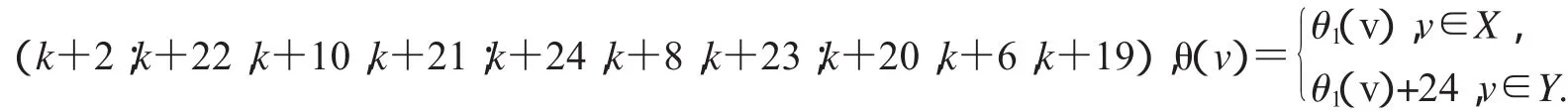
第三种标号为：（k＋36；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

（1）特征为k＋14且缺k＋1，k＋8，k＋19，k＋22和k＋23标号值的交错标号；

（2）缺k＋2，k＋3，k＋8，k＋17和k＋24标号值的优美标号；

设2D3，4如图2所示，设X，Y是图G(k)＋13的一个二分化，θ1是图G(k)＋13的交错标号，且

非连通图2D3，4∪G(k)＋13的各种顶点标号θ定义为：

第一种标号为：（k＋15；k＋12，k＋21，k＋11；k＋14，k＋37，k＋13；k＋10，k＋17，k＋9），

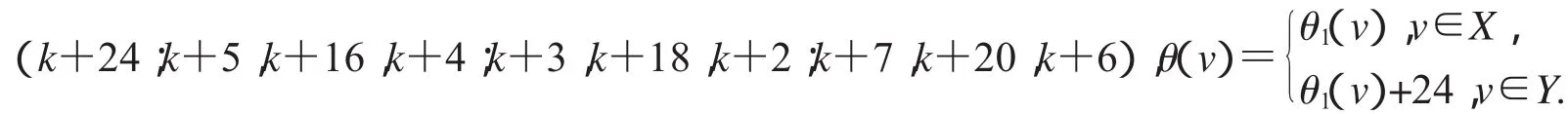
第二种标号为：（k＋10；k＋14，k＋37，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

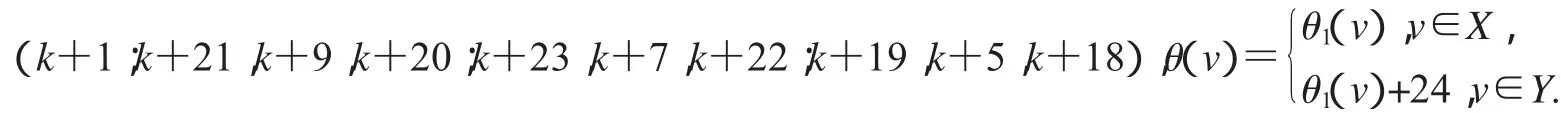
设2D3，4如图2所示，设X，Y是图G(k)＋14的一个二分化，θ1是图G(k)＋14的交错标号，且

非连通图2D3，4∪G(k)＋14的顶点标号θ定义为：

（k＋11；k＋15，k＋38，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

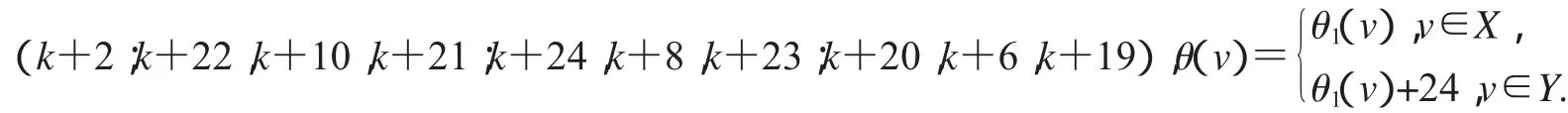
设2D3，4如图2所示，设X，Y是图G(k)＋15的一个二分化，θ1是图G(k)＋15的交错标号，且

非连通图2D3，4∪G(k)＋15的顶点标号θ定义为：

设2D3，4如图2所示，设X，Y是图G(k)＋16的一个二分化，θ1是图G(k)＋16的交错标号，且

非连通图2D3，4∪G(k)＋16的顶点标号θ定义为：

设2D3，4如图2所示，设X，Y是图G(k)＋17的一个二分化，θ1是图G(k)＋17的交错标号，且

非连通图2D3，4∪G(k)＋17的顶点标号θ定义为：

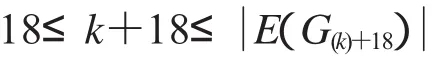
定理16当时，非连通图2D3，4∪G(k)＋18存在

（1）缺k＋3，k＋7，k＋8，k＋17和k＋24标号值的优美标号；

（2）缺k＋6，k＋14，k＋15，k＋22和k＋23标号值的优美标号；

（3）缺k＋1，k＋8，k＋9，k＋17和k＋24标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋18的一个二分化，θ1是图G(k)＋18的交错标号，且

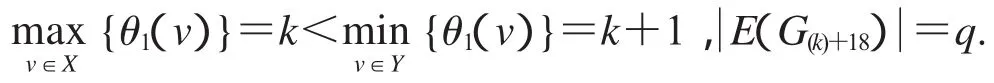
非连通图2D3，4∪G(k)＋18的各种顶点标号θ定义为：

第一种优美标号：（k＋10；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

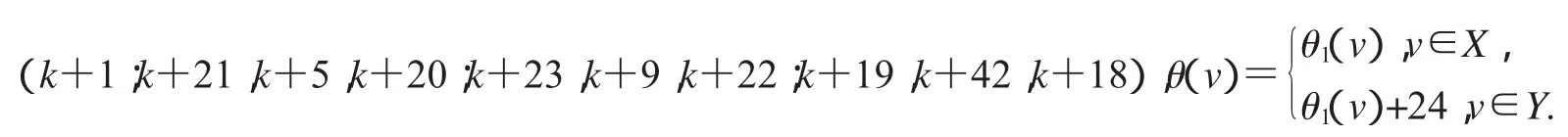
第二种优美标号：（k＋13；k＋10，k＋21，k＋9；k＋12，k＋19，k＋11；k＋8，k＋17，k＋7），

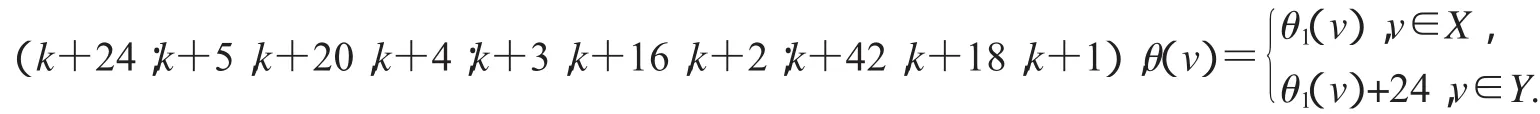
第三种优美标号：（k＋10；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

（1）缺k＋1，k＋4，k＋8，k＋9和k＋18标号值的优美标号；

（2）缺k＋1，k＋2，k＋9，k＋10和k＋18标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋19的一个二分化，θ1是图G(k)＋19的交错标号，且

非连通图2D3，4∪G(k)＋19的各种顶点标号θ定义为：

第一种优美标号：（k＋11；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

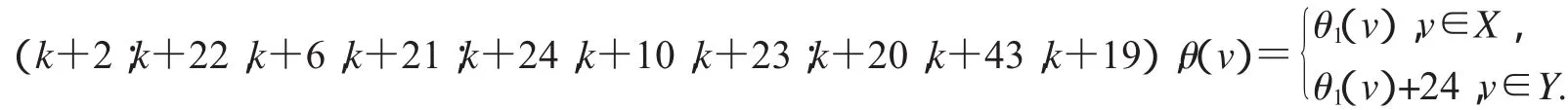
第二种优美标号：（k＋11；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

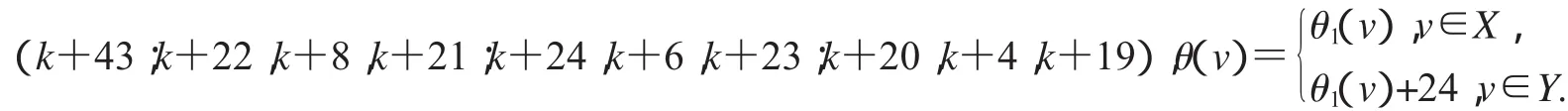
设2D3，4如图2所示，设X，Y是图G(k)＋20的一个二分化，θ1是图G(k)＋20的交错标号，且

非连通图2D3，4∪G(k)＋20的顶点标号θ定义为：

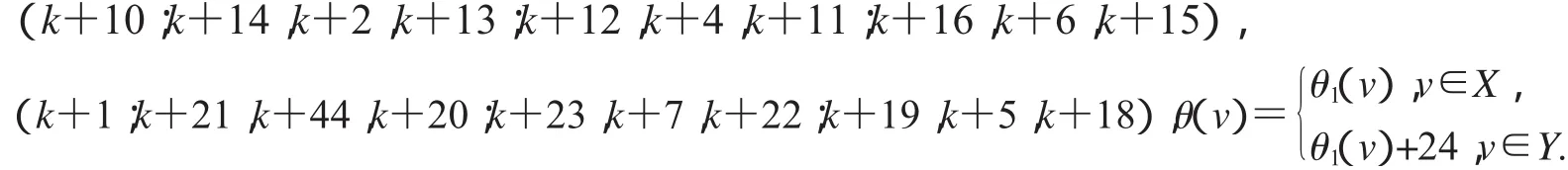
设2D3，4如图2所示，设X，Y是图G(k)＋21的一个二分化，θ1是图G(k)＋21的交错标号，且

非连通图2D3，4∪G(k)＋21的顶点标号θ定义为：

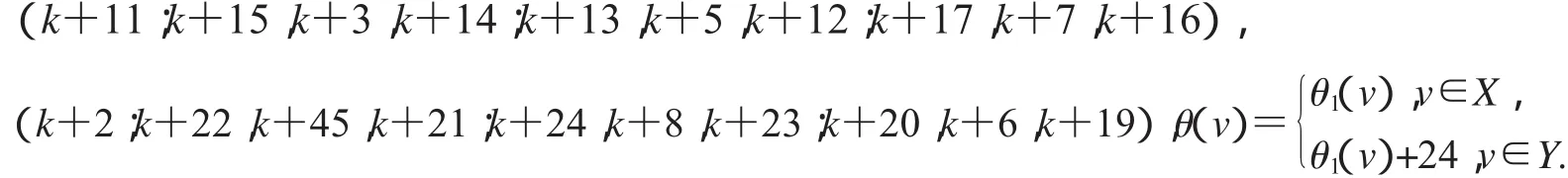
设2D3，4如图2所示，设X，Y是图G(k)＋22的一个二分化，θ1是图G(k)＋22的交错标号，且

非连通图2D3，4∪G(k)＋22的顶点标号θ定义为：

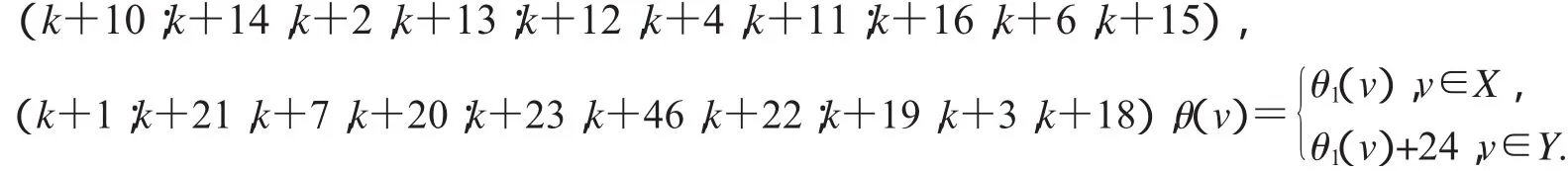
定理21当时，非连通图2D3，4∪G(k)＋23存在缺k＋1，k＋6， k＋9，k＋10和k＋18标号值的优美标号.

设2D3，4如图2所示，设X，Y是图G(k)＋23的一个二分化，θ1是图G(k)＋23的交错标号，且

非连通图2D3，4∪G(k)＋23的顶点标号θ定义为：

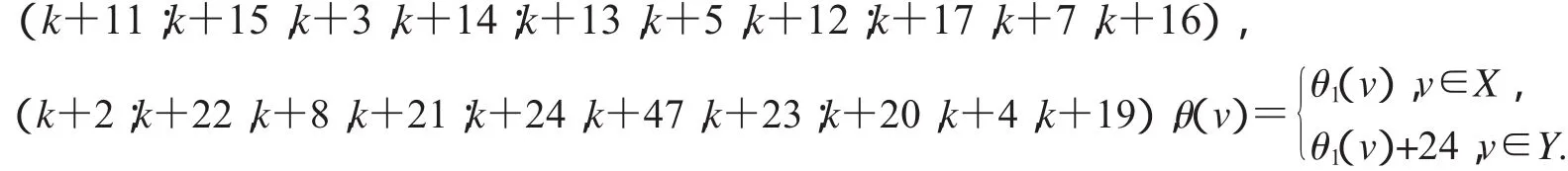
3 结论

本文讨论了非连通图2D3，4∪G的优美性，给出了非连通图2D3，4∪G是优美图的二十一个充分条件.证明了：非连通图2D3，4∪G(k)＋a（a=2，3，4，5，6，8，9，…，23）都是优美的，可为继续研究非连通图sDm，n∪G的优美性提供借鉴.

[1]马克杰.优美图[M].北京：北京大学出版社，1991.

[2]杨显文.关于C4m蛇的优美性[J].工程数学学报，1995，12（4）：108-112.

[3]GALLIANJA.Adynamicsurveyofgraphlabeling[J].TheElectronicJoumalofCombinatorics，2013，16，DS6.

[4]吴跃生，王广富，徐保根.非连通图C4m∪G的优美标号[J].重庆师范大学学报（自然科学版），2015，32（2）：79-83.

[5]吴跃生.非连通图C4m-1∪G的优美标号[J].吉首大学学报（自然科学版），2014，35（3）：1-3.

[6]吴跃生.非连通图D3，4∪G的优美性[J].唐山学院学报，2015，28（6）：3-6.

[7]吴跃生.非连通图L6∪G的优美标号[J].西华大学学报（自然科学版），2015，34（2）：30-35.

[8]吴跃生.非连通图3C4m∪C4m-1∪G的优美标号[J].兰州大学学报（自然科学版），2015，51（1）：115-118.

[9]吴跃生.非连通图2C4m∪C8m-1∪G的优美性[J].东北师范大学学报（自然科学版），2015，47（3）：60-63.

[10]吴跃生.基于路P8m＋4t＋2的交错标号的图S（4m+1，4（t+1），4m-1）的优美标号[J].中山大学学报（自然科学版），2015，54（5）：19-23.

[11]吴跃生，王广富，徐保根.交错图的奇优美性和协调性[J].武汉大学（理学版），2014，60（6）：557-560.

[12]吴跃生.非连通图C4m-1∪C4m∪G的优美标号[J].西南大学（自然科学版），2014，36（8）：83-86

[13]严谦泰.积图Pn×Pm的奇优美性和奇强协调性[J].系统科学与数学，2010，30（3）：341-348.

[14]王涛，闰守峰，李德明.若干并图的优美标号[J].数学的实践与认识，2012，42（16）：201-212.

[15]刘信生，刘元元，姚兵，等.具有奇优美性的一类龙图[J].西南大学学报（自然科学版），2014，36（4）：47-51.

[16]唐保祥，任韩.3类特殊图的优美性[J].武汉大学学报（理学版），2014，60（6）：553-556.

[17]魏丽侠，张昆龙.几类并图的优美标号[J].中山大学学报（自然科学版），2008，47（3）：10-13.

Graceful Labeling of Unconnected Graph 2D3，4∪G

WU Yuesheng
（School of Science,East China JiaotongUniversity,Nanchang330013,Jiangxi,China）

The gracefulness of the unconnected graph 2D3，4∪G is discussed.Twenty-one sufficient conditions are given for the gracefulness of unconnected graph 2D3，4∪G.It is proved that the graph 2D3，4∪G(k)＋aare graceful graph for a=2，3，4，5，6，8，9，…，23

graceful graph;alternating graph;unconnected graph;graceful labeling

O157

A

1001-4217（2017）01-0053-10

2016-01-09

吴跃生（1959—），男，江西瑞金人，硕士，华东交通大学副教授，研究方向为优美标号.E-mail：616100567@qq.com.

国家自然科学基金项目（11261019，11361024）