分母含有平方因子的二项式系数级数

张来萍, 陈艳丽, 及万会

(银川能源学院 基础部，宁夏 银川 750105)

分母含有平方因子的二项式系数级数

张来萍, 陈艳丽, 及万会

(银川能源学院 基础部，宁夏 银川 750105)

根据一个已知级数，使用积分裂项方法得到分母含1个平方因子的二项式系数级数和平方因子与1个、2个、3个的1次因子乘积的二项式系数级数和交错的二项式系数级数．所给出二项式系数级数的和式是函数形式，并给出分母含有平方因子的二项式系数数值级数恒等式．

二项式系数；平方因子；积分裂项；级数

二项式系数在数论、图论、统计和概率等数学分支中扮演重要角色．二项式系数变换问题是组合求和中比较难的课题，是组合数学、解析数学等学科研究领域研究的重要内容，引起了许多组合专家的注意，用各种数学工具得到一系列二项式系数级数重要结果[1-5]，给出一些分母含平方因子的数值级数如

等．文献[6-9]给出多个因子乘积的二项式系数级数．笔者使用裂项法给出分母为奇因子的二项式系数级数，然后以此为基础，用积分-裂项法给出分母含1个平方因子以及平方因子与1个、2个、3个因子乘积的二项式系数级数．利用反三角函数与反双曲函数关系给出分母为平方因子的交错二项式系数级数．最后给出分母含有平方因子的二项式系数数值级数恒等式．因此，利用已知级数使用裂项的方法研究二项式系数变换是组合分析的新方法，也是产生新级数的一个初等研究方法．

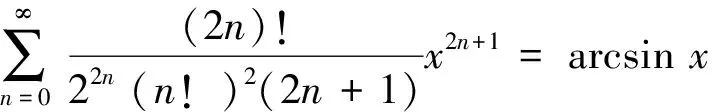
引理2 分母含有1个因子的二项式系数级数为

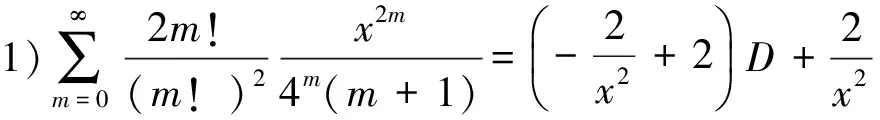
(B1)

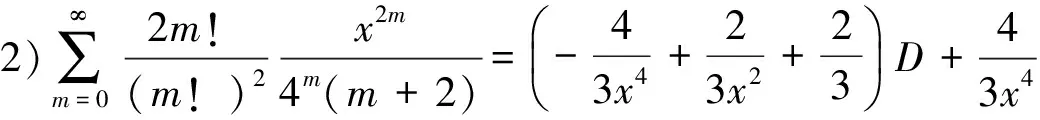
(B2)

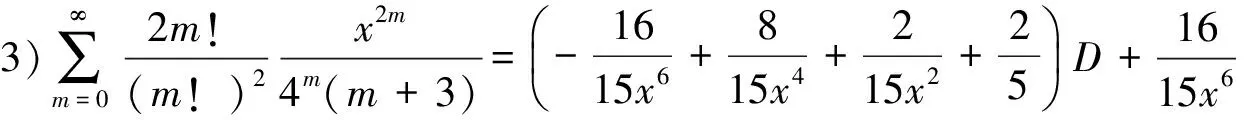
(B3)

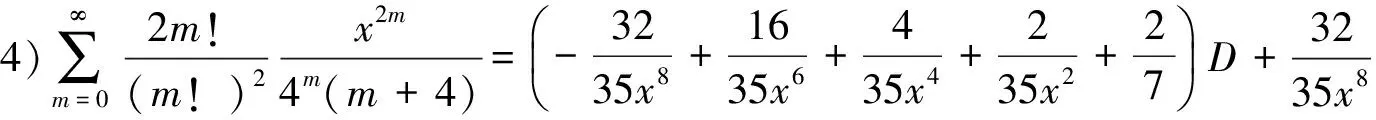
(B4)

(B5)

定理1 分母为奇因子二项式系数级数为

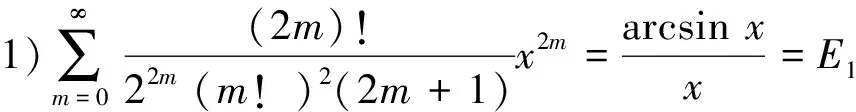
(1)

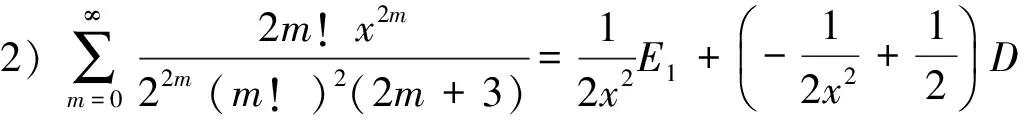
(2)

(3)

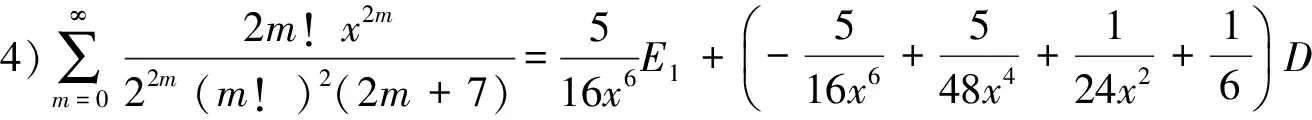
(4)

(5)

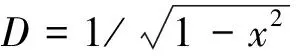
1)分母为1个平方因子的二项式系数级数有

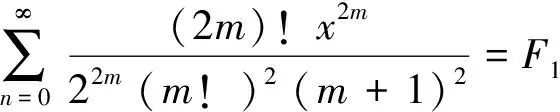
(6)

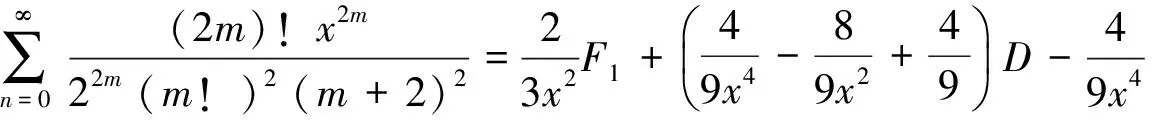
(7)

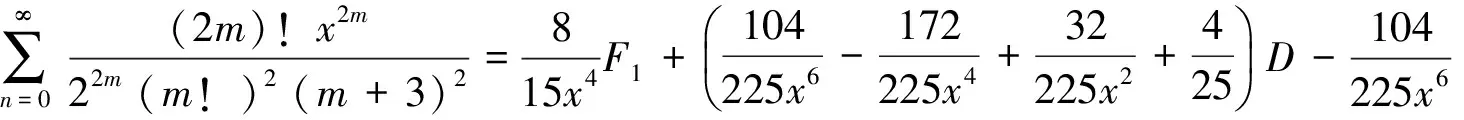
(8)

(9)

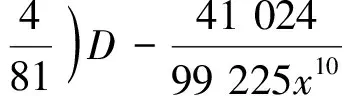
(10)

2)分母平方因子与1个因子乘积的二项式系数级数有

(11)

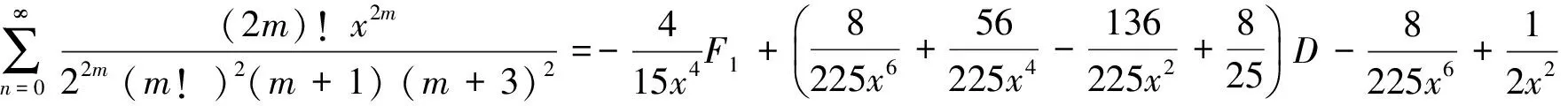
(12)

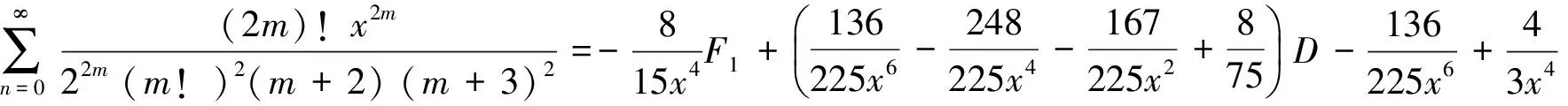
(13)

(14)

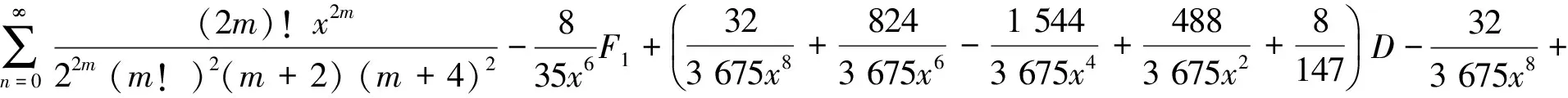
(15)

(16)

3) 分母平方因子与2个因子乘积的二项式系数级数有

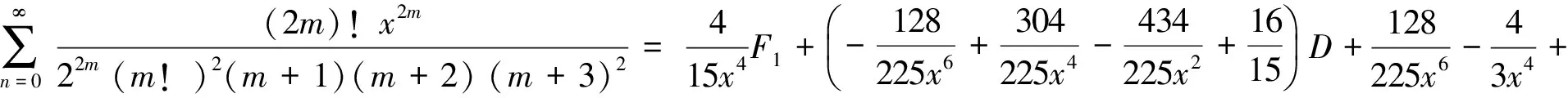
(17)

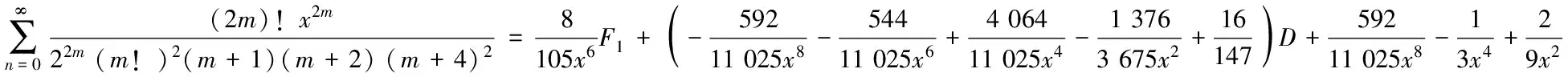
(18)

(19)

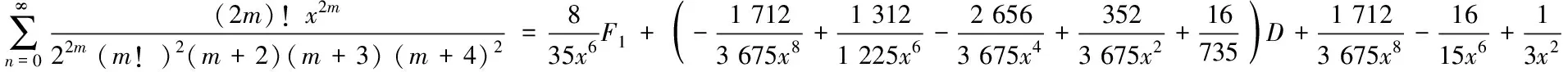
(20)

4) 分母平方因子与3个因子乘积的二项式系数级数有

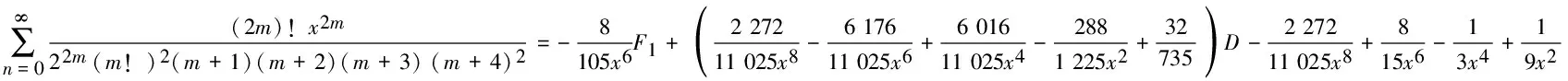
(21)

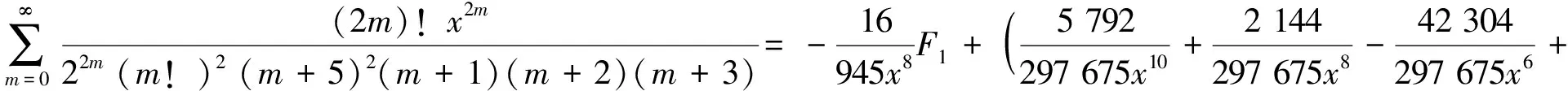
(22)

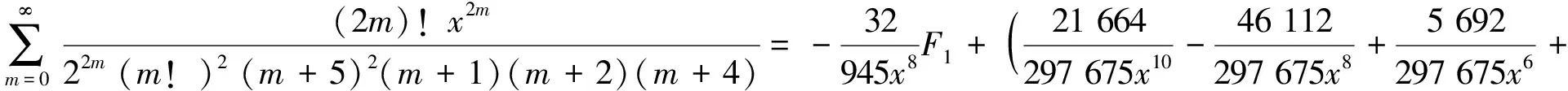
(23)

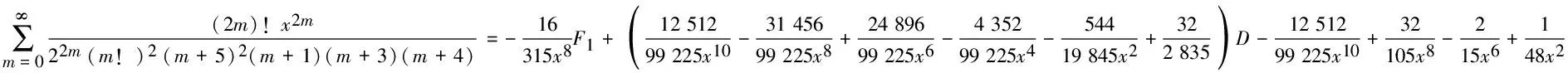
(24)

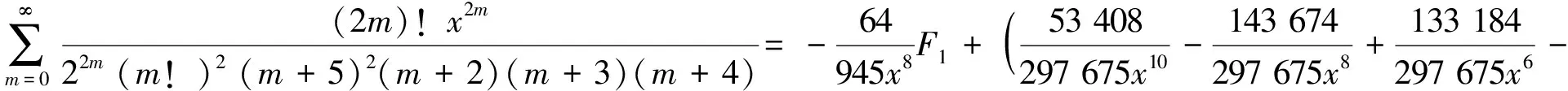
(25)

5)分母平方因子与4个因子乘积的二项式系数级数有

(26)

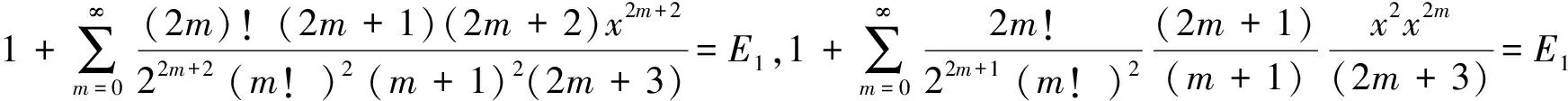
2) 对(1)式继续裂项

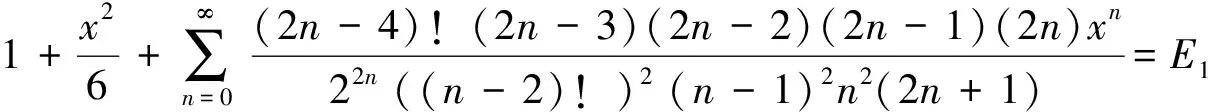
令n-2=m，

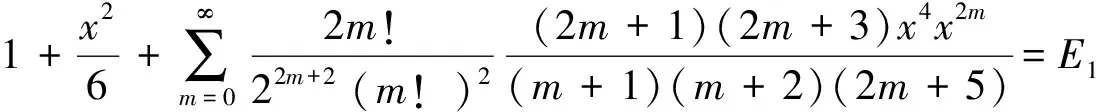
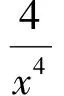
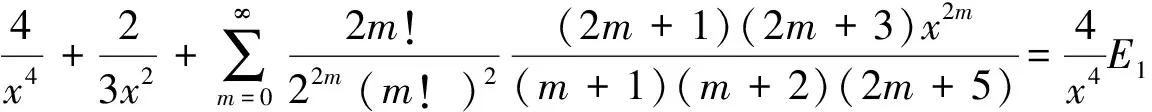
由于B1，B2已知，整理得到(2)式．

3)对(1) 式继续裂项

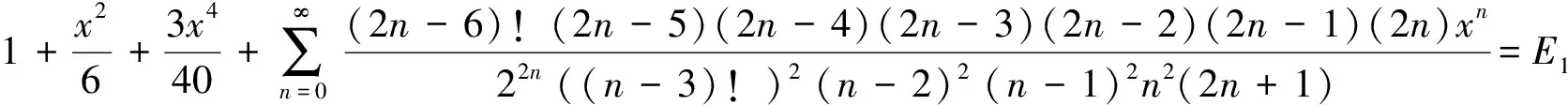
令n-3=m,得

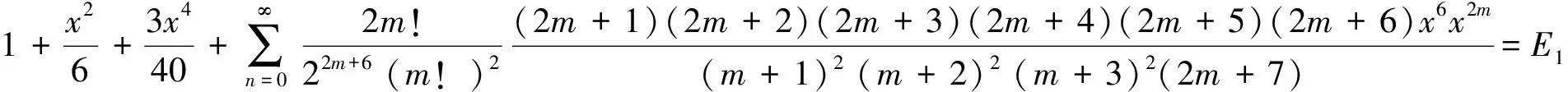
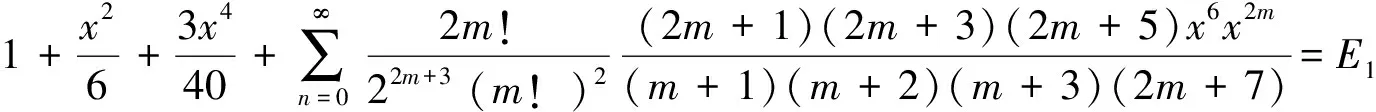
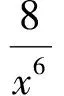
由于B1，B2,B3已知，整理得到 (3) 式．

4) 对(1) 式继续裂项

令n-4=m，

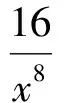
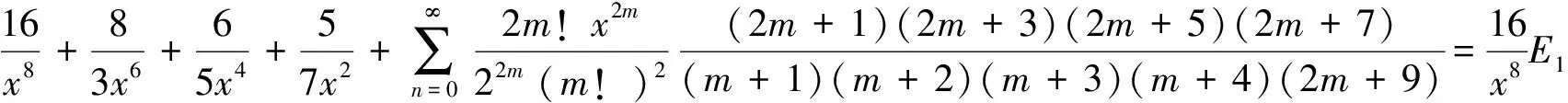
将分式化成部分分式

由于B1，B2,B3,B4已知，整理得到(5)式，定理1证毕．

定理2证明

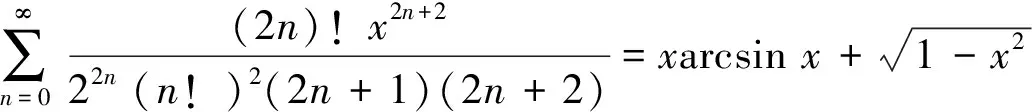
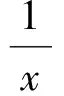
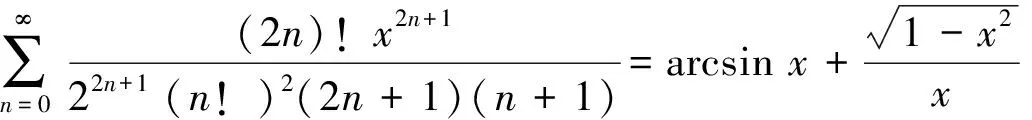
两端对x积分

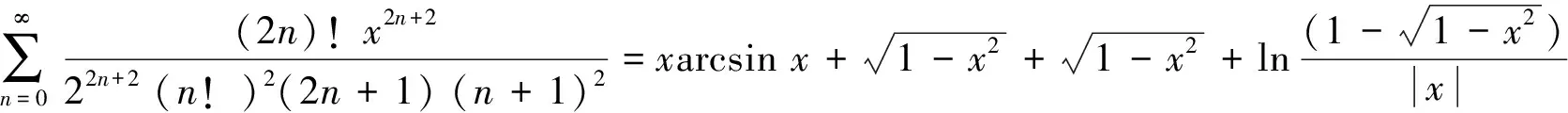
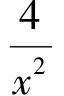
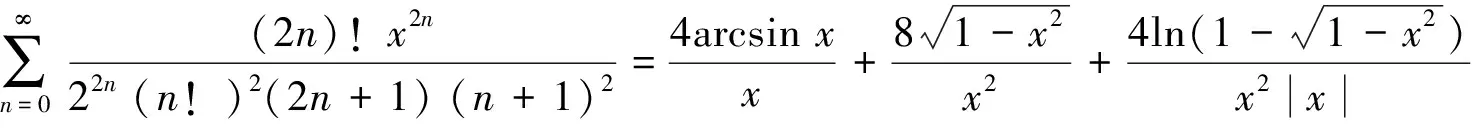
左端分式化成部分分式

由引理2的B1式和(1)式，整理得到(6)式，

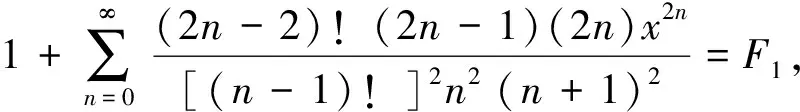
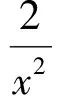
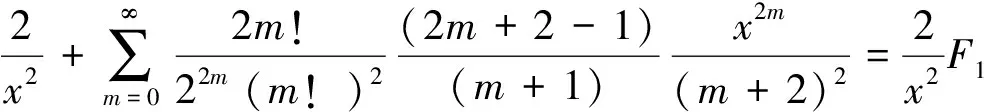
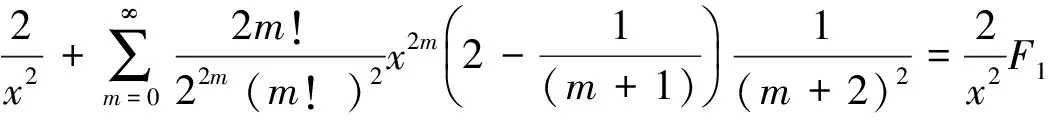
(27)

将(27)式分式分解为部分分式，并将引理2中已知的B1，B2代入，得到(7)式，令其为F2，

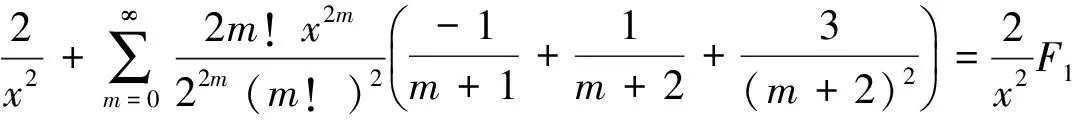
由(27)式和F2，整理得到平方因子与1个因子乘积计算公式(11)．

对(6)式左端继续裂项

令n-2=m，化成

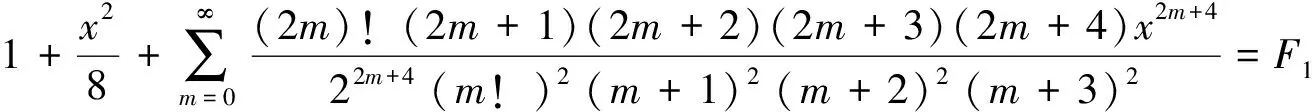
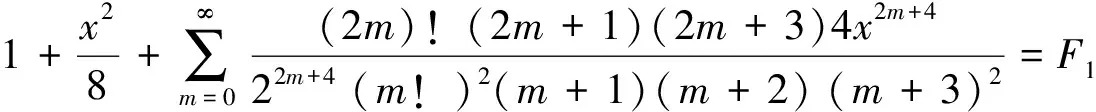
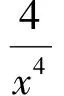
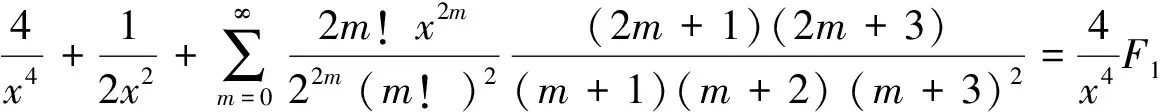
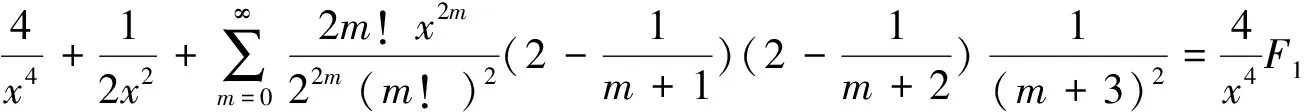
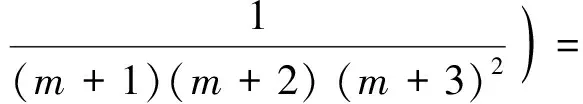
(28)

将所有式分解为部分分式，将引理2已知的B1，B2，B3代入得到(8)式，令其为F3，

(8)

(28)式保留2个因子分式，其他分式化成部分分式，对这2个因子分式每次保留一个，其余化成部分分式得到

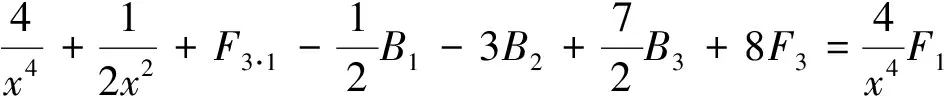
由引理2的B1，B2，B3已知且F3已知，计算可得到(12) 、(13)式．

(28)式保留3个因子分式，其他分式化成部分分式,得到

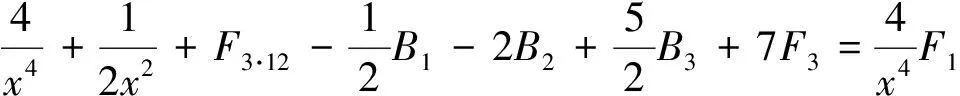
由引理2的B1，B2，B3已知且F3已知，可得到(17)式．

对(6)式左端继续裂项

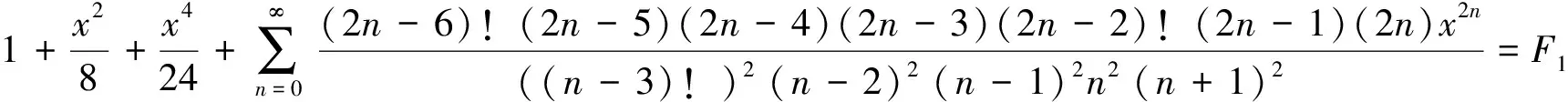
令n-3=m，

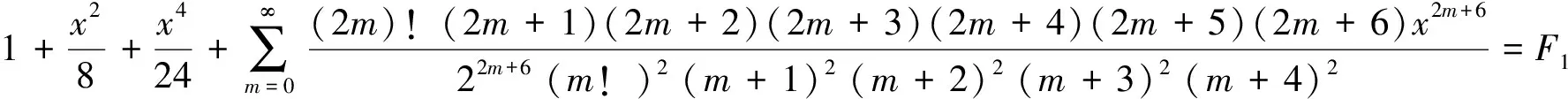
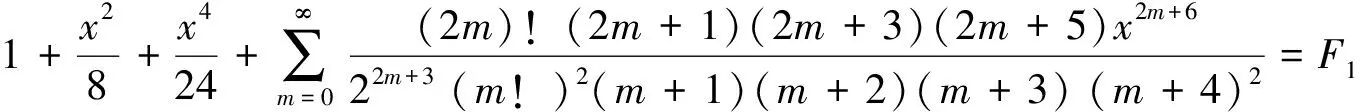
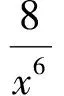
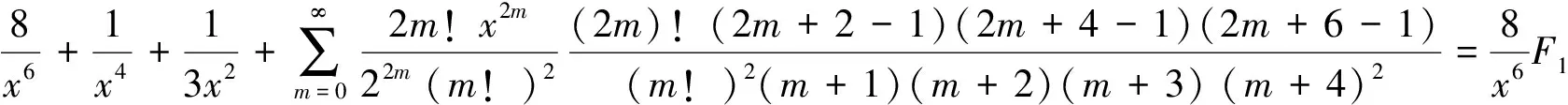
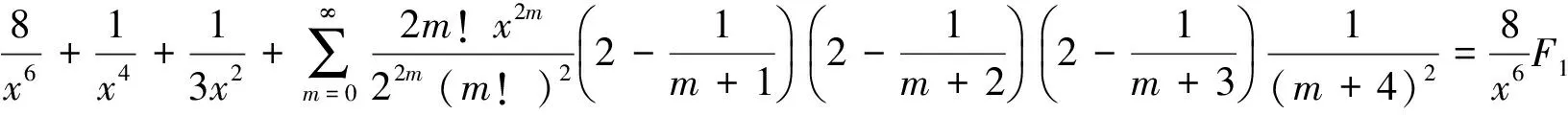
(29)

将(29)式所有分式分解成部分分式

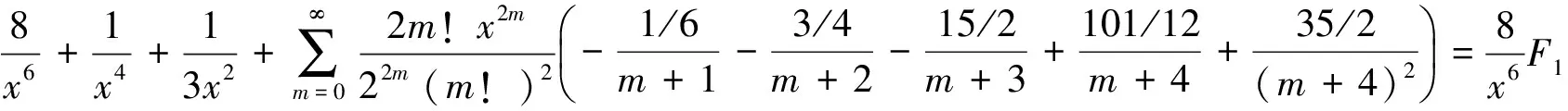
即

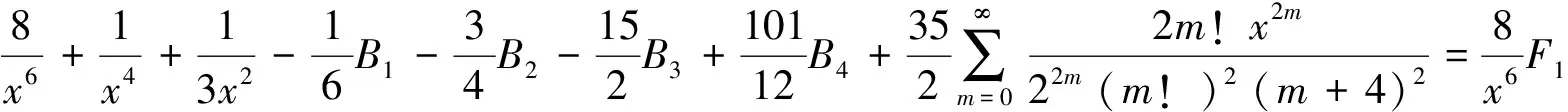
由引理2的B1，B2，B3，B4已知,将其代入并整理得到(9)式，并令其为F4，

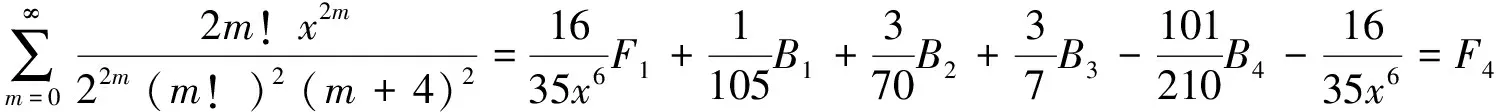
在(29)式保留2个因子分式，然后对这些2个因子的分式，每次保留1个，其余化成部分分式，得到

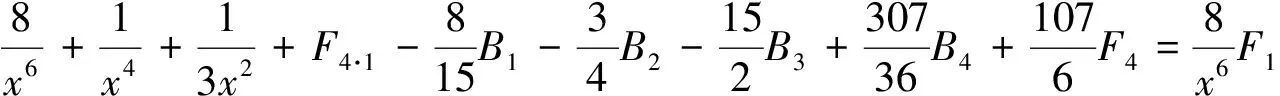
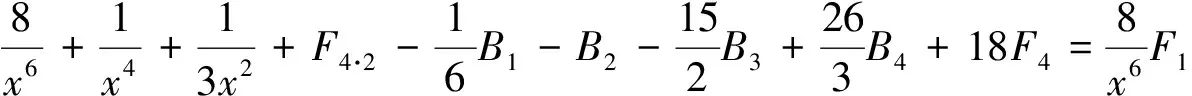
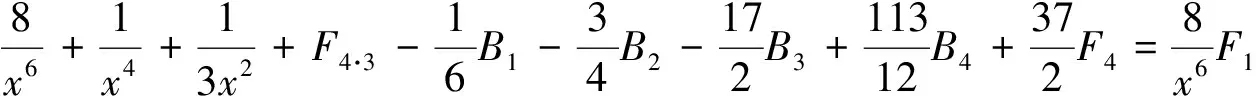
由引理2的B1，B2，B3，B4已知和F4已知，得到(14) ～(16)式．

在(29)式保留3个因子分式，然后对这些3个因子的分式，每次保留1个，其余化成部分分式，得到

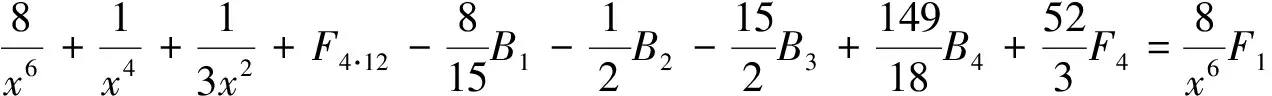
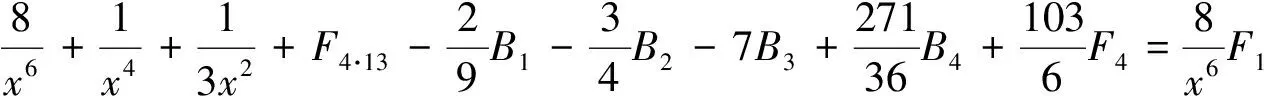
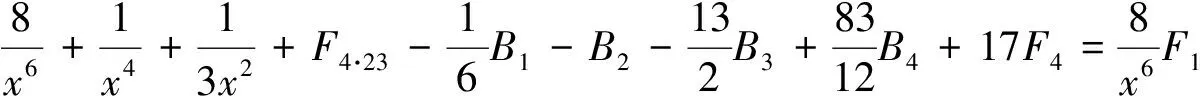
由引理2的B1，B2，B3，B4已知和F4已知，得到(18)～ (20)式．

在(29)式保留4个因子分式，其他分式化成部分分式得到

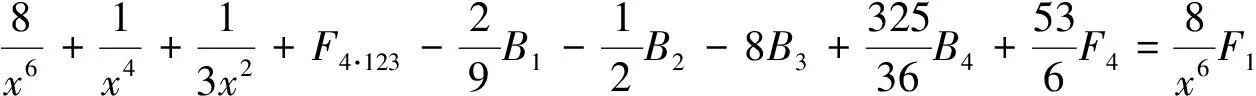
由引理2的B1，B2，B3，B4已知和F4已知，计算得到(21)式．

对(1)式左端继续裂项

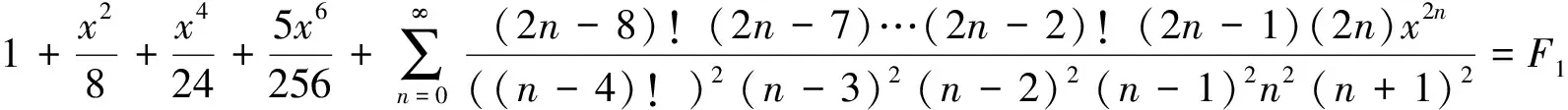
令n-4=m，

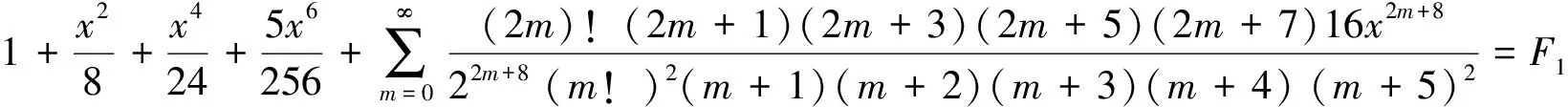
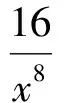
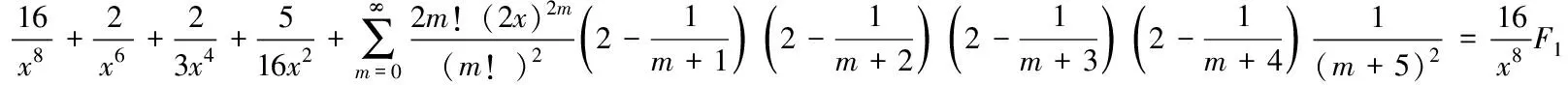
得

(30)

在(30)式可以产生平方因子1个．平方因子与1个因子相乘的公式4个，平方因子与2个因子相乘的公式6个．平方因子与3个因子相乘的公式4个，平方因子与4个因子相乘的公式1个．为简洁起见，这里只求出1个平方因子，平方因子与3个因子相乘及平方因子与4个因子相乘的公式．

将(30)式分解成部分分式，得到

由引理2的B1，B2，B3，B4,B5已知,代入并整理得到(10)式，令其为F5，

(30)式保留4个因子分式，其他分式化成部分分式，对这4个因子分式每次保留一个，其余化成部分分式得到

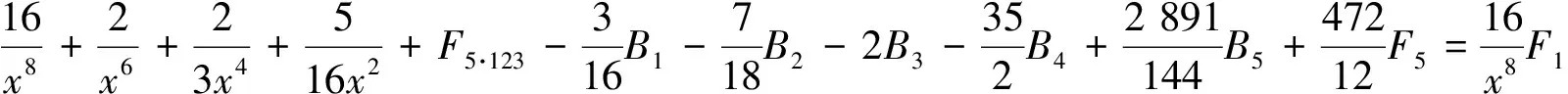
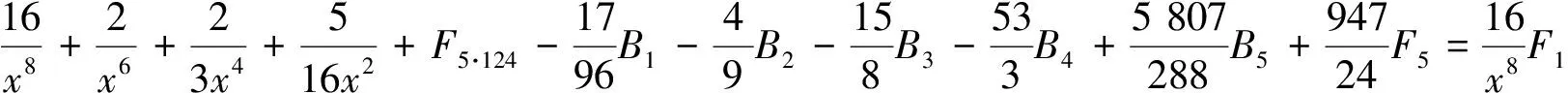
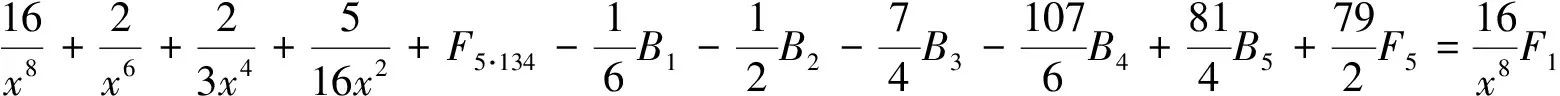
由引理2的B1，B2，B3，B4，B5和F5已知，可得(22) ～ (25)式．

(30)式保留5个因子分式，其他分式化成部分分式得到

由引理2的B1，B2，B3，B4，B5和F5已知计算等式得到(26)式．定理2证毕．

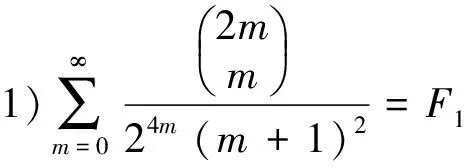
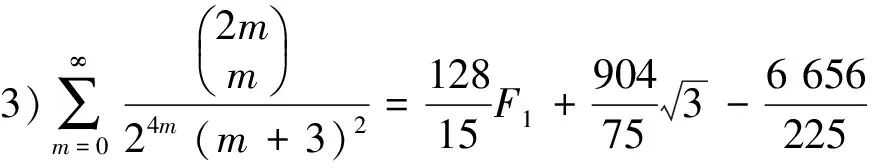
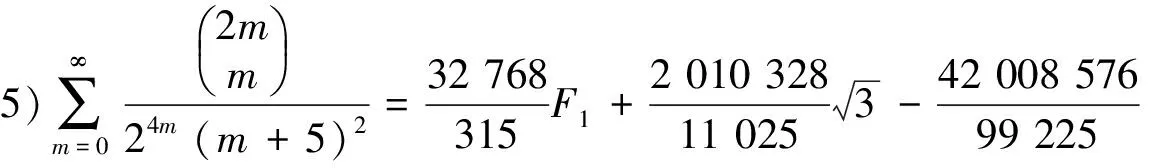
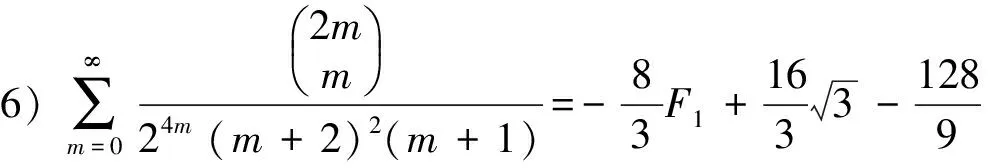
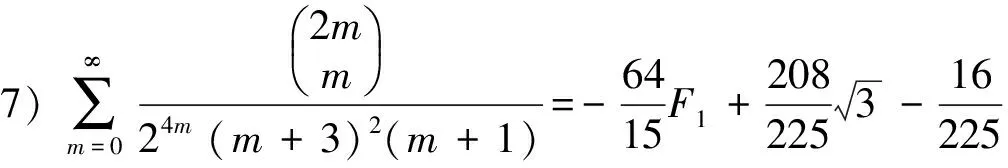
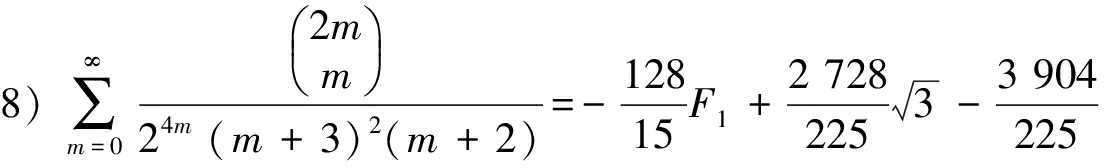
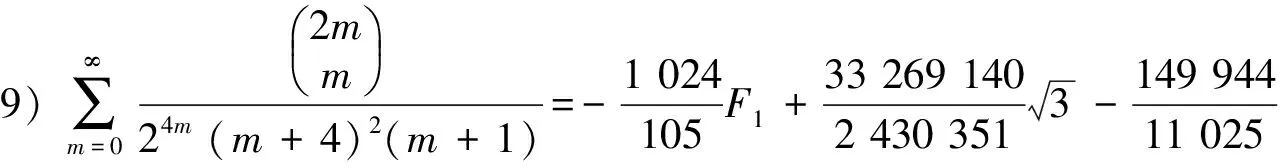
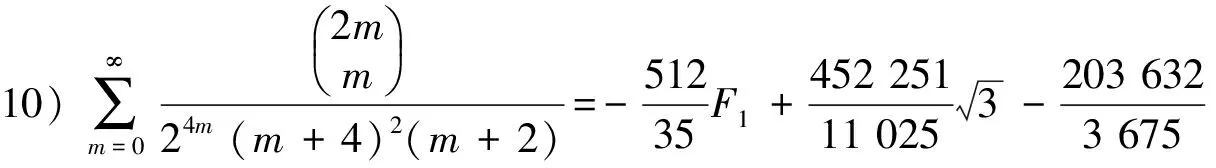
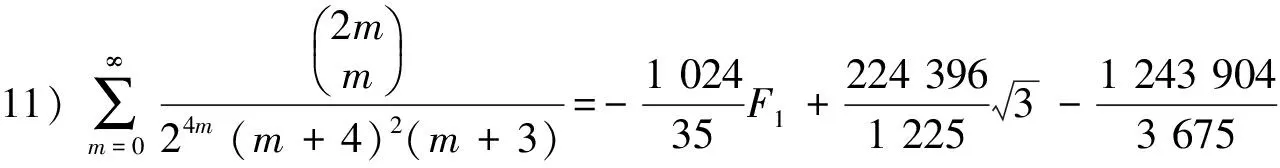
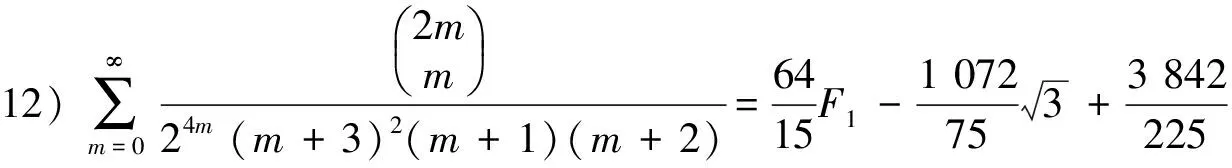
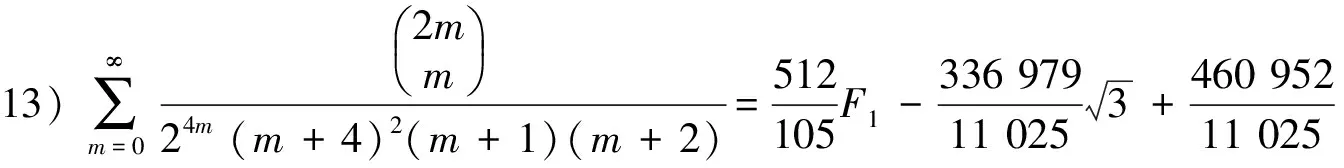
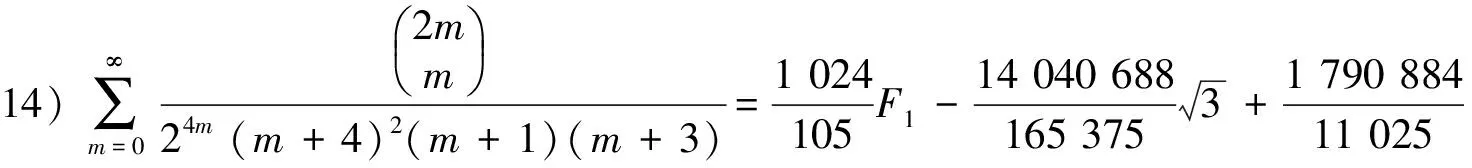
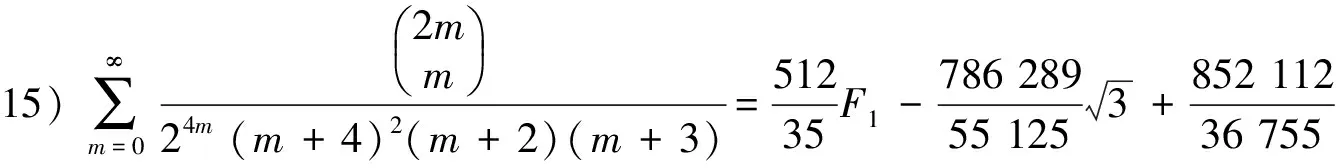
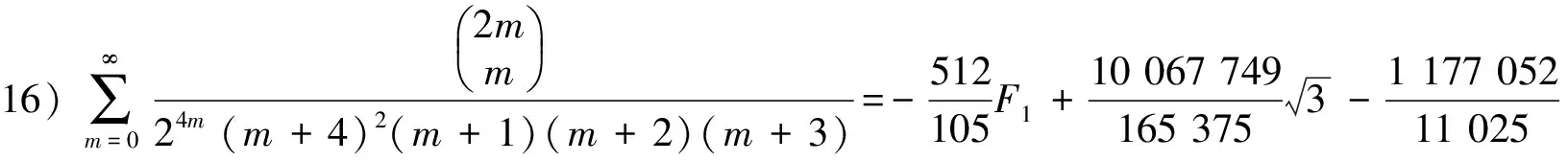
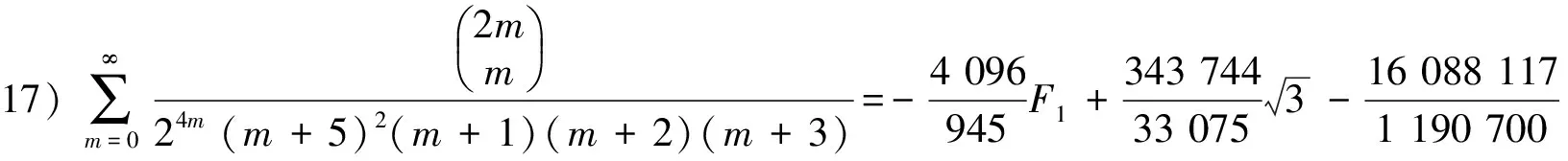
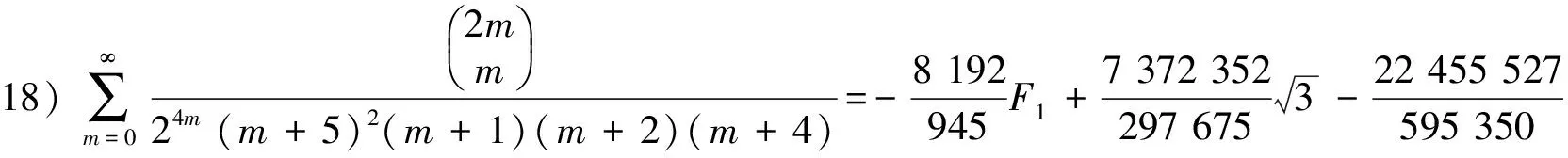
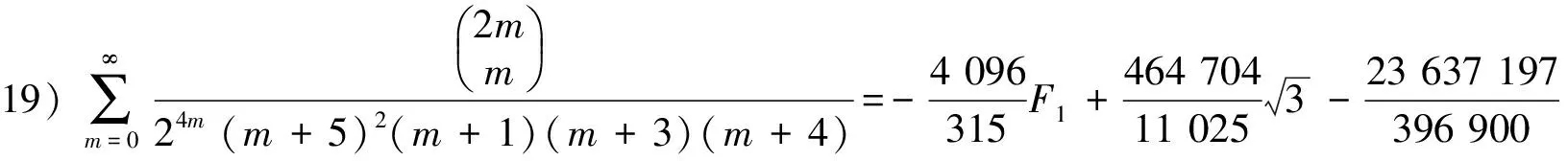
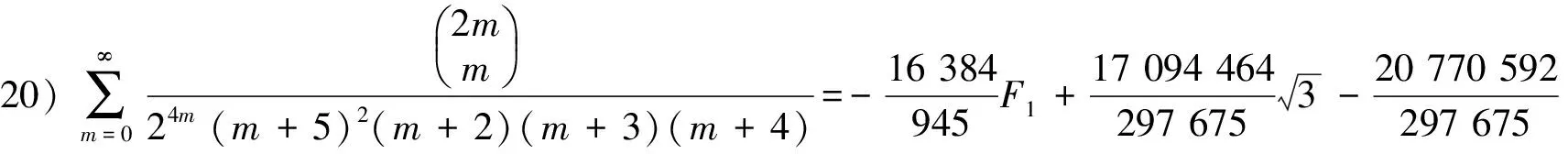
由已知级数用积分-裂项的方法，得到分母含1个平方因子以及平方因子与1个、2个、3个的1次因子乘积的二项式系数级数和交错的二项式系数级数．如果继续使用积分-裂项的方法，可以得到平方因子与p个1次因子乘积的二项式系数级数和交错的二项式系数级数．所给出的级数表达式是函数形式．若给出自变量x的一些数，代入级数表达式可得到许多不同的分母为平方因子的数值级数恒等式．

[1] LEHMER D H．Interesting series involving the central binomial coefficients[J]．Amer Math Monthly，1985 (92)：449-457．

[2] SURY B，WANG TIANNING ，ZHAO FENG ZHEN．Some identities involving of binomial coefficients[J]．Integer Sequences，2004 (7)：2-8．

[3] SOFO A．Integral representations of ratios of binomial coefficients[J]．International Journal of Pure and Applied Mathematics，2006，31(1)：29-46．

[4] BERNDT B C．Ramanujan’s Notebooks[M]．New York：Springer-Verlag，1989：324．

[5] BORWEIN J M，GIRGENSOHN R．Evaluation of binomial series[J]．Aequationens Math，2005，70：25-36.

[6] 及万会,吕汝健．组合数级数和式计算[ J]．西南民族大学学报，2012,38(2):174-182．

[7] 及万会，黑宝骊．关于二项式系数级数恒等式[J]．湖南文理学院学报，2012，24(4)：4-13．

[8] 及万会，张来萍．关于正负相间二项式系数倒数级数[J]．理论数学，2012,2(4)：192-201．

[9] 及万会，黑宝骊．列项法导出二项式系数倒数级数[J]．理论数学，2012,3(1):18-30.

[10]GRADSHTEYN I S，ZYZHK I M．A Table of Integral，Series and Products[M]．Amsterdam：Elsevier，2007：54-61．

Series of Binomial Coefficients of Denominator Containing Square Factors

ZHANG Laiping， CHEN Yanli， JI Wanhui

(DepartmentofBasic,YinchuanEnergyCollege,Yinchuan750105,China)

Using one known series we can structure several new series of binominal coefficients and alternating series of binominal coefficients by integral-splitting items. Their denominator factor has a square, and square factor and 1, 2, 3 product of each factor. And some series of numbers values of binominal coefficients of denominator containing square factors are given.

binomial coefficients； squarer factor； integral-split terms； series

2016-09-18

宁夏自然科学基金项目(NZ12208)；银川能源学院科研基金项目(2015-KY-Y-49)

张来萍(1979—),女，宁夏彭阳人，银川能源学院基础部副教授，主要研究方向：基础数学．通信作者:及万会(1942—)，男，河北泊头人，银川能源学院基础部教授，主要研究方向：数论．

10.3969/j.issn.1007-0834.2017.01.003

O174.5

A

1007-0834(2017)01-0009-10