在类比、转化中实现知识“生长”

姜鸿雁

在类比、转化中实现知识“生长”

姜鸿雁

同学们应该能感觉到，所学新知识常常与旧知识之间有着千丝万缕的联系，我们可以认为，学习数学知识的过程就是知识“生长”的过程.类比、转化这两个基本思想方法是新知生长的“阳光雨露”，对于《分式》这一章内容，同学们如果充分吸收了这些“阳光雨露”，本章知识树不仅能“枝繁叶茂”，还能促进后面的“枝条”茁壮成长！下面，我们来说说如何在旧知识的“土壤”中，吸收“阳光雨露”，实现知识“生长”.

一、知识在类比中“生长”

1.用类比思想把握分式定义的要点.

2.用类比思想理解分式的基本性质.

在学习分数时，掌握分数基本性质是重点，它是将分数进行约分、通分的依据.在类比思想的引领之下，分式的基本性质不仅源于分数基本性质，同样也是对分式进行通分、约分的依据.

【解析】分数约分是对分子、分母分解因数，依据分数基本性质约去公因数，将运算结果化成最简分数或整数.分式约分，则是对分子、分母分解因式，依据分式基本性质约去分子、分母的公因式即可，所以本题结果为：1-2a，分式的运算结果要化成最简分式或整式.分数通分是寻找分母的最小公倍数，分式通分是确定分母的最简公分母.类比无处不在，恰如其分地体现了“数式相通”.

3.用类比思想进行分式运算.

同一切运算的顺序一样，分式的运算也是先乘方，后乘除，再加减，有括号先算括号里面的.在运算过程中，我们还得注意观察式子结构，根据式子结构，有时巧妙运用运算定律，可以达到事半功倍的效果.

例4先化简，再求值：

【解析】按运算顺序、法则，得到化简结果是4

x2+2x.在求值环节，固然可以考虑先把方程解出来，然代入x的值求得最后结果，但解后的值肯定带根号，再代入会较烦琐.仔细观察分式化简结果以及方程结构，把x2+2x看成一个整体，可以轻松得到结果为.思维起步源自仔细观察，养成良好的观察习惯，是提升思维品质的开始.

4.用类比思想掌握分式方程的应用.

用数学模型刻画实际生活中的数量关系是数学学习的目的之一，学过一元一次方程、二元一次方程（组）的定义、解法之后，我们便可以试着应用相关数学模型解决实际问题.基本步骤是：审清题意，寻找实际问题中的相等关系；设出适当未知数，表示上述数量关系，从而列出方程（组）；解方程（组）；检验；给出结论.类比分式方程的应用，也是如此，只是所列方程是分式方程，对方程的解进行检验时，不仅要检验是否符合实际情况，还需检验是否方程的解（防止出现增根，后面将重点提及）.

例5两个小组同时从甲地出发，匀速步行到乙地，两地相距7500m，第一组步行速度是第二组的1.2倍，比第二组早15min到达乙地.求第一小组的速度.

二、知识在转化中“生长”

1.体现转化思想主要知识点.

一元一次方程（最简单的整式方程）的解法是解分式方程的“土壤”，在转化思想的“浇灌”之下，解分式方程便算不上什么新知识.除此之外，异分母分式的加减运算，是经过通分化异分母分式加减为同分母分式加减.这些知识点，无不体现化陌生为熟悉的学习历程.

例6（2016·贵州黔东南州）解方程：

【解析】对于有分母的方程，在方程左右两边同时乘最简公分母（x-1）（x+1），可以去分母，从而得（x+1）2-4=x2-1，这一步将分式方程转化为整式方程，解这个整式方程，得x=1.

2.运用转化思想应特别注意的两点.

（1）产生增根的原因.

在例6中，分式方程求解过程似乎已经结束，回首化分式方程为整式方程的“细节”：在方程左右两边同时乘（x-1）（x+1），这是含有未知数的代数式（根据分式方程的定义，最简公分母注定含有未知数），注意不是常数，这预示着什么？从浅层次说，最简公分母的值将随x的取值变化而变化，如果x的取值使最简公分母的值为0，则转化的过程“违反”了等式基本性质，所以要对解出的整式方程的解进行检验，看看有没有“违反”等式基本性质，也就是验证最简公分母为不为0，对去分母这一步给出“回应”；从深层次讲，这使方程解的范围扩大了（因为分式的定义要求分母不为0，而这个规定在去分母后，不再存在），所以要对所转化而来的整式方程的解检验.以例6为例：x=1恰好使最简公分母值为0，所以x=1只是转化后的整式方程的解，对于分式方程来说是增根，原分式方程无解.

因此，在化陌生为熟悉的过程中，必须兼顾数学学科严谨的特性.只要真正理解增根产生的原因，无论是解分式方程还是用分式方程解决实际问题，都不会忘记检验这一重要环节.

（2）增根的特点.

深入思考增根产生的过程，不难发现增根的两大特征：使最简公分母的值为0；是转化后的整式方程的解.应用这两个特征，可以解决一些相关问题.

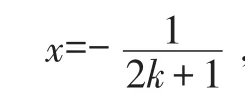
（3）分式方程无解与增根的关系.

对于可化为一元一次方程的分式方程来说，出现增根，则意味着原分式方程无解，但若分式方程无解，不一定只有分式方程有增根这一种情况.为什么？追溯解分式方程的步骤：通过去分母、化分式方程为整式方程，然后解整式方程，最后对整式方程的解检验.若转化后的整式方程无解，则分式方程必无解.所以若分式方程无解，可能有两种情况：一是转化后的整式方程无解；二是转化后的整式方程的解是分式方程的增根.

【解析】化分式方程为整式方程并整理得：（2+a）x=3，分类讨论：①当a=-2时，整式方程无解，则分式方程一定无解；②当分式方程有增根，则x=1，它满足转化后的整式方程，代入整式方程，得a=1（说明：x=0不是分式方程增根，因为此时a无解）.所以a=-2或1.

进一步思考，若分式方程有解，则必须满足转化后的整式方程有解且此解不是增根.

【解析】转化分式方程为整式方程并整理得：（5-a）x=10，首先确保整式方程有解，则a≠5，再考虑x≠0且x≠2，由此得a≠0，所以本题选D.

纵观本章内容，一个个知识点是从分数、一元一次方程等知识节点中“生长”出来的.在类比与转化思想的“引领”之下，在整体思想的“帮衬”之下，在“求同存异”的“包容”之下，实现了新知与旧知的无缝对接.同样的道理，它也将成为后面即将要学习的内容的“生长”节点.

（作者单位：江苏省无锡市河埒中学）