“正弦定理”的教学设计、实践与反思

●

(宁波市第二中学 浙江宁波 315000)



“正弦定理”的教学设计、实践与反思

●韩蕾

(宁波市第二中学 浙江宁波 315000)

“正弦定理”是《数学(必修5)》的第1节课，文章通过融入数学文化史进行定理的引出、证明、赏析和应用.

正弦定理；历史发展；核心素养

2017年3月，笔者所在学校举行了以“关注核心素养，关注课堂教学”为主题的同课异构活动.笔者有幸参加了这次活动，与另一位来自重庆南开中学的教师分别执教了“正弦定理”这节课.现将本堂课的教学设计、实践与反思作一呈现，期待与同行交流.

1 教学过程

1.1 追根溯源，引入定理

师：昨天，夜空迎来了一次奇妙的天象：双星伴月.不知有没有同学见证了这一时刻呢？人民网上发布了一张照片：金星、火星和月亮近距离相聚，形成一张美丽的笑脸.当我带着孩子仰望夜空时，孩子问我：妈妈，月亮离我究竟有多远呢？这是一个不可及物体距离的测量问题.类似这样的实际问题你们能举出例子来吗？

生1：测量我们学校旗杆与月湖里女神像间的直线距离(笔者所在学校处在美丽的月湖风景区).

生2：测量高楼大厦建筑物的高度.

生3：测量海上两个岛屿间的距离.

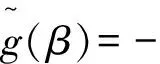
样本空间是色子的6个点数构成的集合，对应的概率分布列如表2所示.

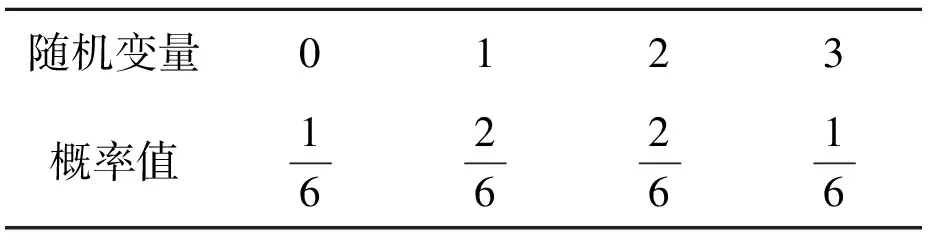
表2 6个点数构成的样本空间所对应的概率分布列

比较两个分布列可以看出，表1中任何一个随机变量对应的概率值的分子正好是表2中对应随机变量概率值的分子的6倍.而前者样本空间中的等可能性事件的个数也正好是后者样本空间中等可能性事件个数的6倍.这就使得两个分布列中对应随机变量的概率值始终相等.

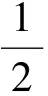
贝特朗概率悖论促进了概率公理化体系的建立.再次分析该悖论，仍然让我们有所启发.

[1] 伯特瑟卡斯， 齐齐克利斯.概率导论[M].2版.郑忠国,童行伟，译.北京:人民邮电出版社,2016.

[2] 单墫.高中数学教学参考书·数学3(必修)[M].南京:江苏教育出版社,2012.

[3] 严士健,刘秀芳.测度与概率[M].2版.北京:北京师范大学出版社,2006.

师：解决这些问题，我们现有的几何知识够用吗？在这一章，我们将要学习的“解三角形”就可以用来解决这些问题，它一般研究三角形边与角之间的关系，属于“三角学”的范畴.古往今来，许多数学问题的产生也是来源于观测天体、航海、地理现象等等，最初的三角学就是起源于天文学.古希腊的天文学家在研究天体运动中推动了“球面三角”的萌芽，随着航海和地理的发展，人们在研究球面三角的过程中得到了一个副产品“正弦定理与余弦定理”.这两个定理非常重要，它们为建立平面三角奠定了基础[1].我们这一章要学的就是这两个重要的定理.今天我们先来学习第1个定理：正弦定理.

设计意图从“双星伴月”的天文奇象引出关于不可及物体的距离测量问题，让学生感觉自然亲近，也调动了课堂气氛.本节课是章首课，因此有必要介绍这一章要学什么，为什么要学.穿插简单的数学史，让学生感受正弦定理并非只是冰冷的公式，它和人类生命一样，是一个美丽的产物.

1.2 归纳猜想，证明定理

师：在Rt△ABC中，用锐角三角函数来表示边与角的关系.记AB=c,AC=b,BC=a，如何用边来表示角？

师：这两个等式都有一个共同的分母，能否利用这一特点将两个等式合并成一个等式呢？

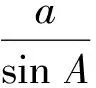
师：很好.你们感受到了这个等式的特点吗？

生(部分)：分子为边长，分母为边所对角的正弦值.

师：有没有美中不足呢？

生6：少了关于另一条边的式子.

师：完美！通过对直角三角形边与角的研究，我们归纳出了一个形式对称的式子.请大家猜想：这个式子能适用于斜三角形中吗？

生(众)：应该可以.

师：那好，接下来我们试着在斜三角形中进行证明.

先在锐角三角形中进行证明，由于学生事先已经预习过，因此大部分学生都能较快地找到方法(作高).

生8：如图1，在△ABC中作高AD，构造出两个直角三角形，通过计算AD得到式子

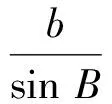
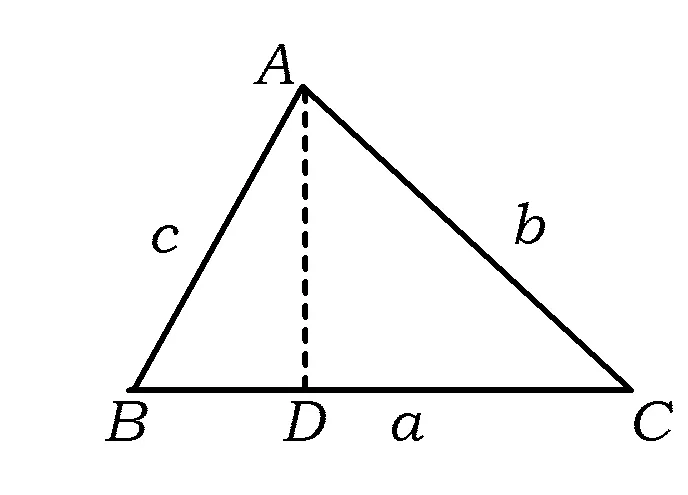
图1

师：将锐角三角形分割成两个直角三角形，这是“化斜为直”的解决方法，通过对同一个对象进行“算两次”的方法，建立起了边与角的关系，非常好.

虽然有刺激性气味可能不环保，但没有刺激性气味也不等于环保。除了甲醛，室内还有苯、氨、TVOC、放射性氡等多种有害气体，其中放射性气体氡是无色、无味、无法察觉的惰性气体。因此最真实有效的办法就是请专业机构用专业仪器检测。

师：在钝角三角形中的证明，留给同学们课后自己去完成.这就是我们今天要学习的正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即

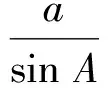
设计意图通过“归纳—猜想—证明”的过程，让学生体会从特殊到一般的学习方法.在证明过程中，渗透“化斜为直”“算两次”的解题方法.

1.3 “圆”来如此，赏析定理

生(众)：直角三角形的斜边长.

师：那么在斜三角形中呢？这个比值还会是c，抑或是其他的值？

通过师生共同努力，利用外接圆法，找到了比值为三角形外接圆的直径，从而得到

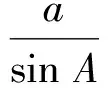
然后利用思维导图的形式(如图2)，引导学生将正弦定理进行了深度赏析.

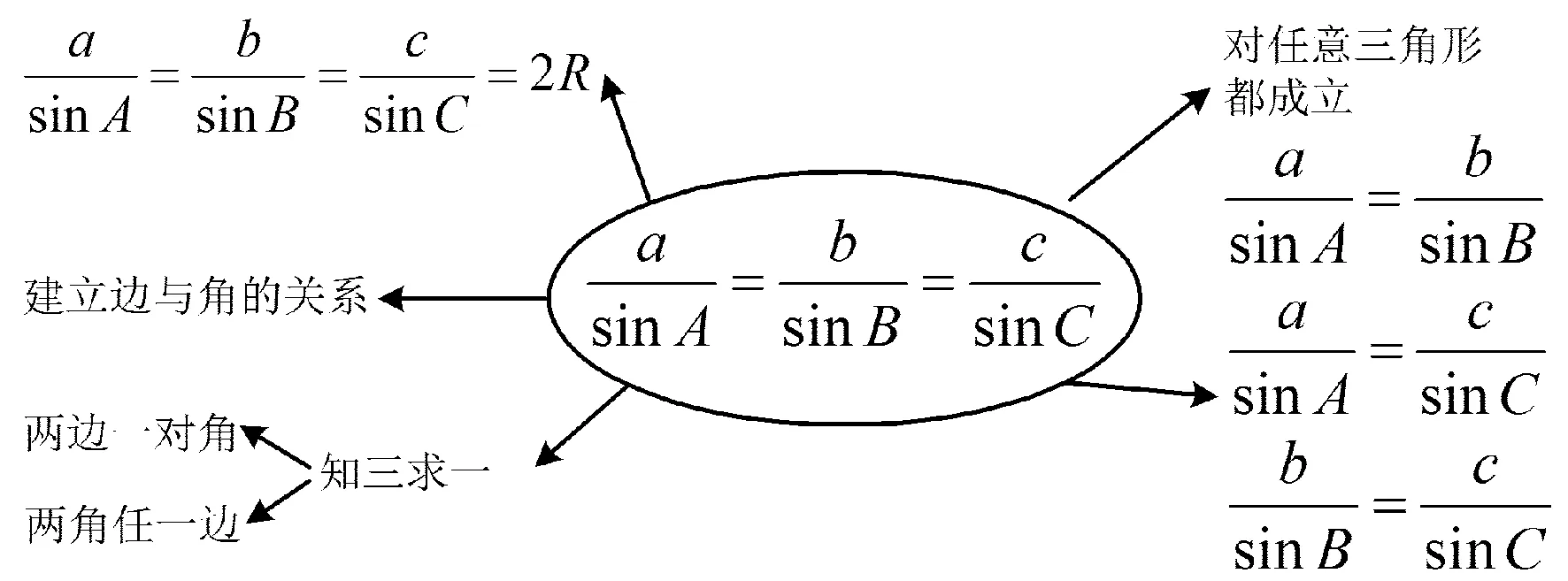
图2

师(PPT展示图片)：我们只用了约20分钟赏析了该定理，可是正弦定理的发展并不是如此一帆风顺的.最早是阿拉伯的数学家阿布尔提出了平面三角的正弦定理，然后在1030年，另一位数学家阿尔毕鲁尼首次对定理进行了证明.又过了400多年，在1464年，德国数学家雷格蒙塔努斯在他的著作《论各种三角形》中清晰地将定理展示出来.当然，又过了很漫长的一段时间，人们才慢慢地接受并应用正弦定理[2].历史的发展赋予了正弦定理以内在美，公式本身又向我们呈现出它的形式美.接下来让我们继续探究正弦定理的应用价值.

设计意图通过引入圆来得出正弦定理的几何意义，渗透数形结合的思想.介绍正弦定理简单的发展历史，让学生在冰冷的数字背后感受到正弦定理的生命力和数学的内在美，体现数学的核心素养.1.4 知识拓展，应用定理

例11)在△ABC中，已知A=45°,B=60°,c=1,求C,a,b.

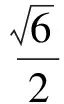
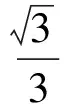
课后探究对课前问题“测量学校旗杆与月湖里女神像之间的直线距离”提出测量方案.

设计意图例1中的3个小题是针对正弦定理的基础训练，其中第2)和第3)小题是两边一对角的类型，一题为两解，一题为一解.留给学生课后思考三角形个数的问题，为下一节课作好铺垫.对测量实际距离提出测量方案，让学生感受到数学知识可以服务于生活，是一门有用的学科.

1.5 总结反思，感悟定理

师：请大家说说本节课中你学到了什么，对于数学学习有哪些体会呢？

师生共同总结：

一个定理：正弦定理；

两种方法：化斜为直、算两次方法；

三种思想：类比转化、从特殊到一般、数形结合思想.

布置作业(略).

2 课后感悟

“正弦定理和余弦定理”并不是在学生用量角器、刻度尺、计算器测量任意三角形的边与角中产生的，它们的产生和三角学的发展息息相关.因此就有了以上的融入数学史的教学设计.

2.1 渗透历史，体会数学之美

有人将一堂课比作一道菜，这道菜的味道如何，一方面取决于厨师的厨艺，另一方面还取决于食材是否丰富.对于正弦定理，本身是一个冰冷的公式，于学生而言，学习的目的似乎就是为了应付考试，会算即可.如果仅仅从直角三角形的找边角关系引入，或是从某一个实际问题的计算引入，那么学生就感受不到定理本身的内涵美.

笔者从三角学的发展历史入手，简单地介绍了正弦定理产生的过程.在赏析定理的过程中，再次提出正弦定理漫长的发展过程，让学生感受到：正弦定理并不是一个冰冷的公式，它也是有生命的，是一个美丽的公式.渗透数学的历史文化，让这节课显得不那么单调，上课的“食材”也就显得丰富多元.

2.2 联系实际，凸显定理价值

在课的开始与结尾，笔者都提出了不可及物体距离的测量问题，前后呼应.在应用定理环节，除了让学生完成常规的解三角形题型外，还留给学生课后探究的练习题，以凸显正弦定理的应用价值，也让学生感受到数学可服务于生活，从而培养他们的应用意识.

2.3 关注学生，体现核心素养

数学的核心素养是数学教与学过程中应当特别关注的重点.在本节课中，笔者的设计遵循两条线：一条明线为“引入定理—证明定理—赏析定理—应用定理—感悟定理”；一条暗线为正弦定理的简单发展历史.让学生从中不断地经历推理论证、定理内涵的挖掘，从知识上加深对概念、定理的理解.数学史的引入也绝非简单的移植和嫁接，在恰到好处的地方进行数学文化史的渗透，以做到润物细无声.

当然，教学是一门遗憾的艺术.当我们在反思一堂课时，总会有这样或那样的不满.笔者期待同行们的批评与指正，以期在课堂教学的路上走得更踏实.

参考文献

[1] 张国定.HPM视角下的数学教学设计——从正弦定理的教学设计谈起[J].数学教学研究，2010(3)：14-16.

[2] 陈克胜.“余弦定理和正弦定理”的数学思想史略[J].数学通讯，2004(21)：45-47.

2017-03-21；

2017-04-25

韩 蕾(1982-)，女，浙江舟山人，中学高级教师.研究方向：数学教育.

O124.1

：A

：1003-6407(2017)07-27-03