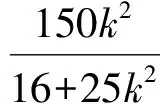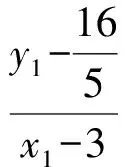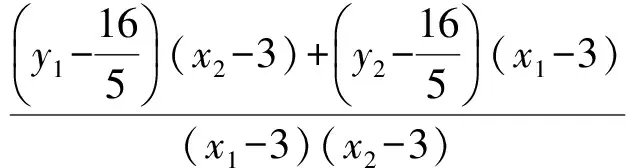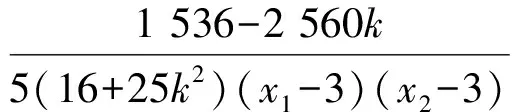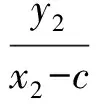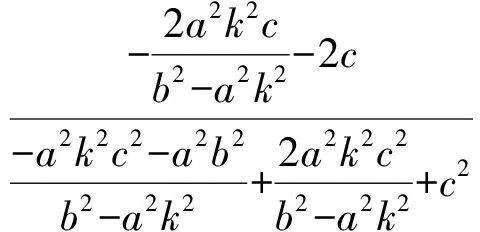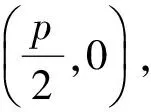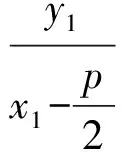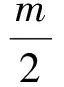探究割补法在求解抛物线内接三角形面积问题中的应用

●

(开元中学 浙江杭州 310016)



探究割补法在求解抛物线内接三角形面积问题中的应用

●陈巧

(开元中学 浙江杭州 310016)

抛物线与三角形是初中数学的核心内容，它们的有机结合可以构建综合题和探究型的试题，特别是抛物线内接三角形面积问题,更是成为各地数学中考的热点题型，而割补法在解决此类题型时具有明显的优势.文章以一道中考复习题为例，通过灵活运用割补法来深入探究抛物线内接三角形的面积问题.

抛物线;内接三角形;割补法

抛物线内接三角形是指3个顶点都在抛物线上的三角形,它在有关二次函数的习题中经常出现,也是初中数学学习的难点之一.内接三角形的面积问题，由于涉及知识面广、综合性强,使得很多学生不知如何下手.笔者在长期的教学中发现，若学生能灵活掌握割补法，则能大大提高解决此类问题的正确率.所谓割补法，就是把不规则的图形通过等面积替换，转换位置，使不规则图形变成规则图形，以便使用公式求解的一种方法.这种数形结合的割补法，可以大大减少计算量，同时对于引导学生透过表象把握问题本质、培养学生举一反三的解题能力具有一定的指导意义[1].下面，笔者通过一道中考复习题来详细说明割补法在求解抛物线内接三角形面积问题中的实际应用.

1 引入割补法求解

例1已知二次函数y=x2-2x-3，设函数与x轴交于点A,B(其中点A在点B的左边)，与y轴交于点C，顶点为D.

1)求△BCD的面积;

2)若点P是抛物线上位于直线BC下方的一个动点，试求△BCP面积的最大值;

3)问：抛物线上是否存在点Q，使得S△BCQ=S△BCD?

本题具有典型性，整个题目都是围绕抛物线内接三角形面积问题展开的.在第1)小题中，易求得B(3，0)，C(0，-3)，D(1，-4)，从而本题可看作是根据三角形的3个顶点坐标来求三角形的面积.由于此类三角形为非特殊三角形，不便直接使用面积公式求解，但可用割补法来解决.以下提供4种常规的割补方法：

方法1如图1，根据S△BCD=S矩形OBNM-S△OBC-S△BDN-S△CDM即可求解.

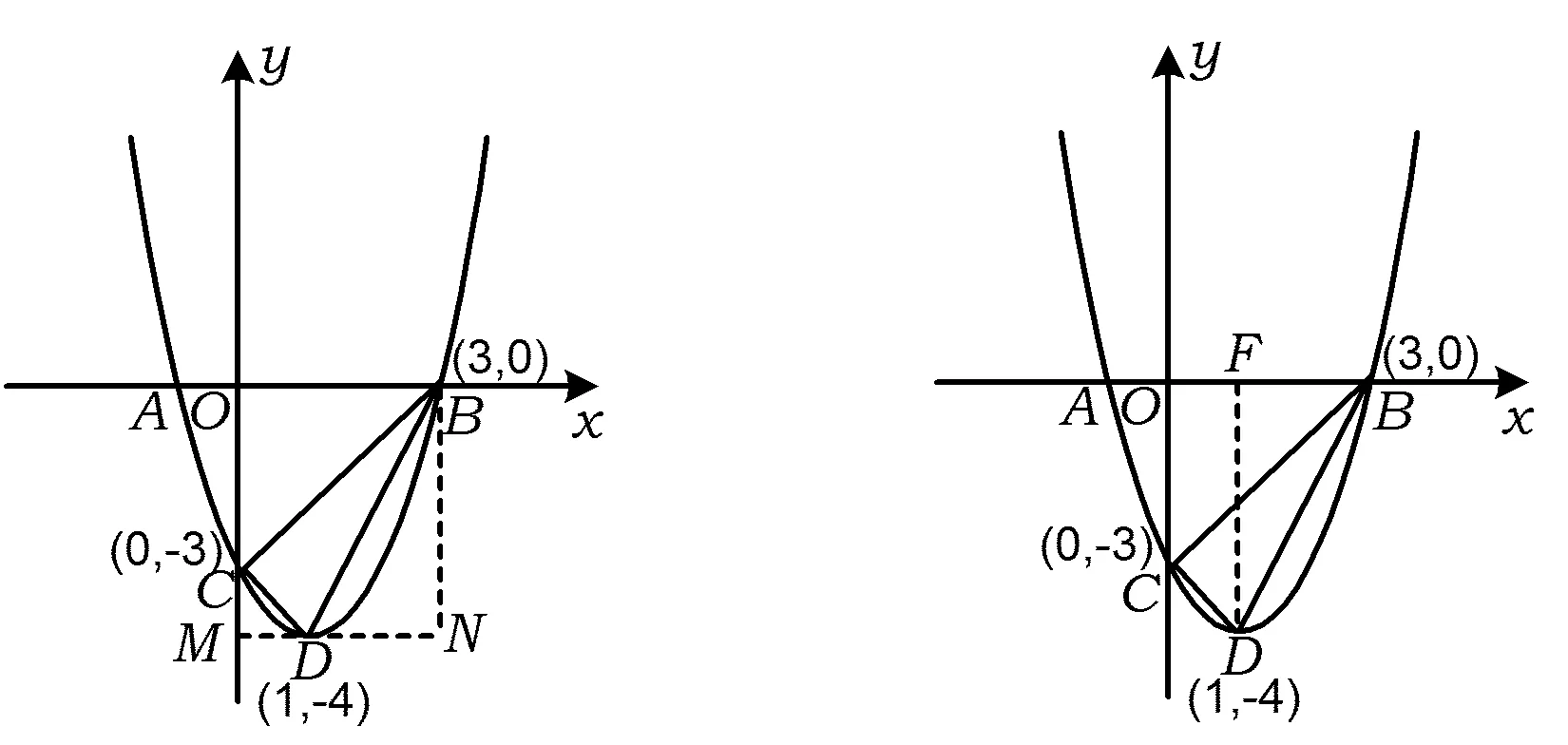
图1 图2

方法2如图2，根据S△BCD=S梯形OCDF+S△BDF-S△OBC即可求解.

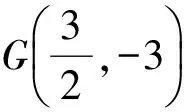
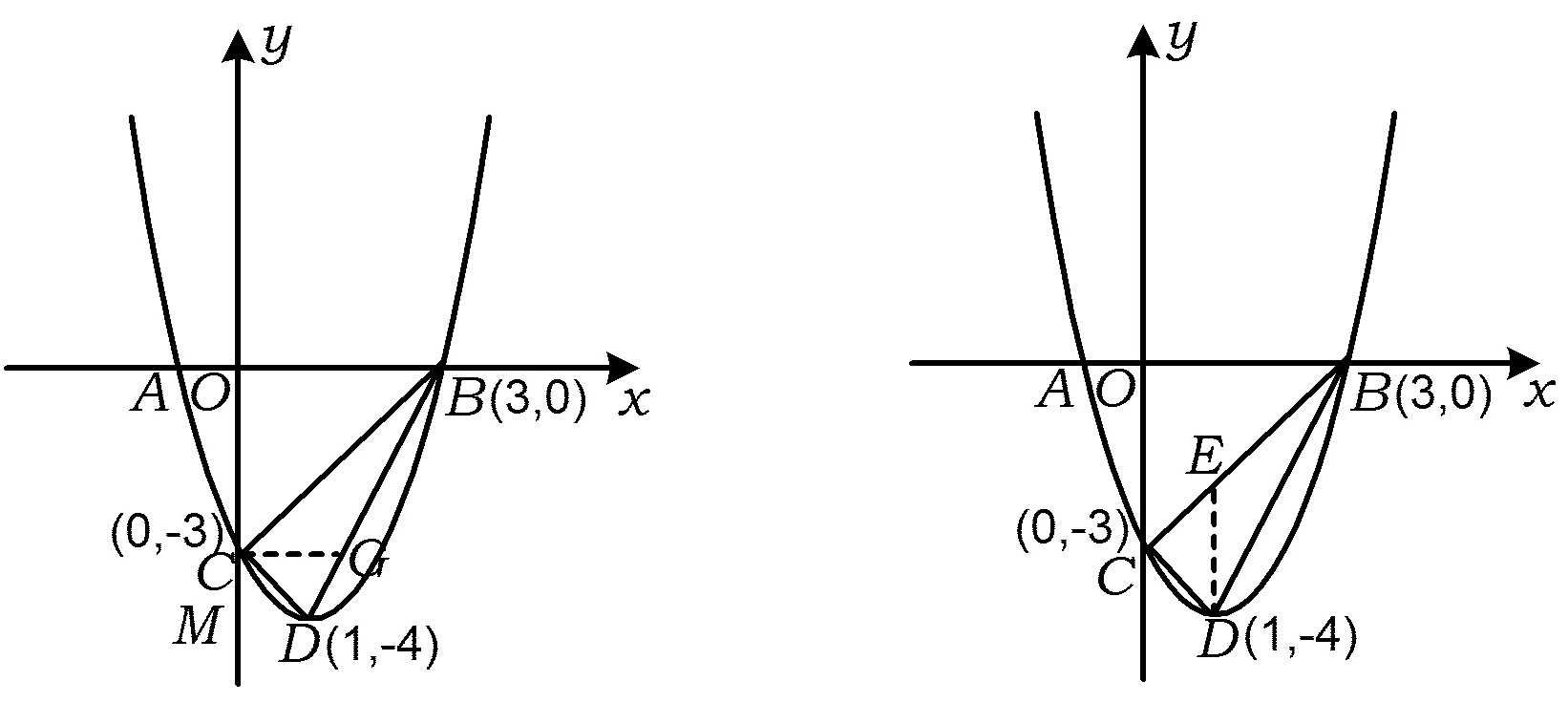
图3 图4

方法4如图4，易求得直线BC的方程为y=x-3,从而E(1,-2)，根据S△BCD=S△BED+S△CED即可求解.

不难看出：方法3和方法4的解题原理是一样的，都是将一个三角形分割成两个三角形，然后利用共有的底求解.这种割补法是比较常规的方法，学生比较容易理解，但若要将其上升到普遍规律的高度，进而得出固定的解题公式，则有点难度.

2 割补法的拓展延伸

图5

事实上，如图5，过△ABC的3个顶点分别作出与水平线垂直的3条直线l1,l2,l3,其中直线l2与直线AB相交于点D.记l1与l3之间的距离为△ABC的“水平宽(记作a)”，线段CD的长度为△ABC的“铅垂高(记作h)”.在方法4中，水平宽a即为线段BO的长,铅垂高h即为线段DE的长，从而

h=EP=(m-3)-(m2-2m-3)=-m2+3m,

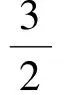
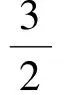
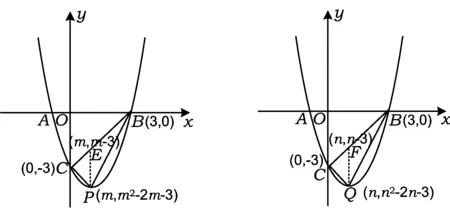
图6 图7

h=FQ=|(n-3)-(n2-2n-3)|=|-n2+3n|，

易求得S△BCD=3，从而

在此小题中，点F不一定在线段BC上(即点F不一定在点Q上方)，故FQ=|(n-3)-(n2-2n-3)|=|-n2+3n|.事实上，当点F不在线段BC上时(如图8)，

S△BCQ=S△BGF-S△BGQ-S△QFC=

图8 图9

3 割补法的解法应用

通过上述解题论证不难发现，割补法在求解抛物线内接三角形面积问题时都可以适用.

例2如图9，抛物线的顶点坐标为C(1，4)，交x轴于点A(3，0)，交y轴于点B.

1)求抛物线的解析式和△CAB的面积.

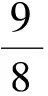
分析1)如图9，易得抛物线的解析式为y=-x2+2x+3，从而点B的坐标为(0，3)，进而可得直线AB的解析式为y=-x+3.过点C作CD∥y轴交AB于点D,得点D的坐标为(1,2).在△CAB中，水平宽a=3，铅垂高h=2，于是

图10

2)如图10，因为点P在抛物线上，所以可设P(m,-m2+2m+3).过点P作PG∥y轴交AB于点G,得点G的坐标为(m,-m+3).在△PAB中，水平宽a=3，铅垂高

h=|-m2+2m+3-(-m+3)|=|-m2+3m|，

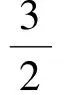
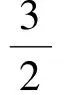
4 结束语

数学作为一门科学，必然有其规律可循.笔者通过详细讲解割补法在求解抛物线内接三角形面积问题中的应用，目的就是寻找这种规律性.作为一线教师，在平常的教学过程中，不能满足于向学生生硬地灌输课本知识，而是要通过对规律的探究，使学生不仅知其然，还要知其所以然.割补法在实际应用中千变万化，只有对其作进一步地提炼，如文中所探讨的“引入‘水平宽’和‘铅垂高’的概念”，从而将这种割补法以公式的形式固定下来.只有这样才能使学生掌握割补法的要义，也才能使学生以不变应万变，灵活应用，提高解题的效率和正确率.

[1] 余献虎，邵婉.分析法——解决数形结合型几何问题的有效策略[J].中学教研(数学)，2015(10)：37.

[2] 王汉超.与抛物线的内接三角形面积有关的中考题[J].数学大世界:初中版，2002(3)：32-33.

[3] 汤列.抛物线内接三角形面积的最大值问题的解法探究[J].数理化解题研究:初中版，2015(5)：41-42.

1)求椭圆的标准方程;

2)若k1+k2=0，求实数k的值.

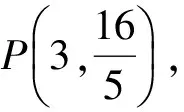
从而

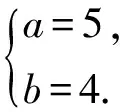
2)①当0

得

(16+25k2)x2-150k2x+225k2-400=0.

设A(x1,y1),B(x2,y2),则

由y1=k(x1-3),y2=k(x2-3),得

故

③当k不存在时，此时斜率k1,k2均不存在，不合题意.

通过研究笔者发现:点P正好是过右焦点作垂直于x轴的直线与曲线的交点(位于x轴上方)，而所求k正好是离心率，并发现这不是巧合.

对于第2)小题可作如下变式推广.

解1)当0

得 (b2+a2k2)x2-2a2k2cx+a2k2c2-a2b2=0.

设A(x1,y1),B(x2,y2),则

又

解得

kPA+kPB=-2e.

3)当k不存在时，斜率kPA,kPB均不存在，不合题意.

解1)当0

得 (b2-a2k2)x2+2a2k2cx-a2k2c2-a2b2=0.

设A(x1,y1),B(x2,y2),则

又

解得

kPA+kPB=2e.

3)当k不存在时，斜率kPA,kPB均不存在，不合题意.

设A(x1,y1),B(x2,y2),则

于是

2k-m=-2,

即

2)当k=0时，A(0,0)，点B不存在，则kPA=-2，kPB不存在.

3)当k不存在时，斜率kPA,kPB均不存在，不合题意.

以上就是对这道赛题的一般推广，请读者批评指正.

参考文献

[1] 丁龙云.2016年全国高中数学联合竞赛[J].中等数学,2016(11):21-27.

2017-03-29；

2017-04-30

陈 巧(1986-)，女，浙江杭州人，中学二级教师.研究方向：数学教育.

O123.1

：A

：1003-6407(2017)07-46-03