On the C 1 Regularity of Solutions to Divergence Form Elliptic Systems with Dini-Continuous Coefficients∗

Yanyan LI

(Dedicated to Haim Brezis on his 70th birthday with friendship and admiration)

1 Introduction

This note addresses a question raised to the author by Haim Brezis,in connection with his solution to a conjecture of Serrin concerning divergence form second order elliptic equations(see[1]and[2]).If the coefficients of the equations(or systems)are Hölder continuous,then H1solutions are known to have Hölder continuous first derivatives.The question is what minimal regularity assumption of the coefficients would guarantee C1regularity of all H1solutions.See[3]for answers to some other related questions of Haim.

Consider the elliptic system for vector-valued functions u=(u1,···,uN),

where B4is the ball in Rnof 4 centered at the origin.The coefficientssatisfy,for some positive constantsΛ andλ,

and

where

M ain TheoremSuppose thatsatisfy the above assumptions,andis a solution of the elliptic system.Then u is C1in B1.

Remark 1.1For elliptic equations with coefficients satisfying α-increasing Dini conditions,a proof of the C1regularity of u can be found(see,e.g.,[6,Theorem 5.1]as pointed out in[1–2]).

Question 1.1If we replacein(1.3)by

2 M ain Results and Proofs

Let Br(x)⊂Rndenote the ball of radius r and centered at x.We often write Brfor Br(0),and r B1for Br.Consider elliptic systems

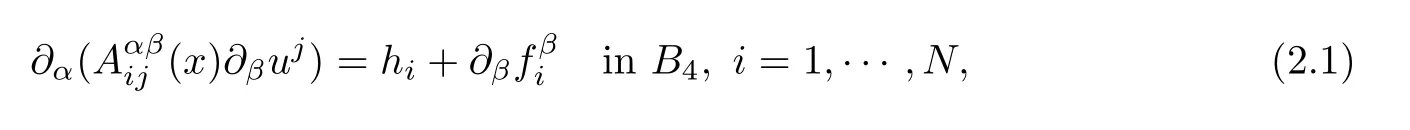
whereα,β are summed from 1 to n,while i,j are summed from 1 to N.The coefficientsoften denoted by A,satisfy,for some positive constants Λ and λ,(1.1)–(1.3),withgiven by(1.4).

Theorem 2.1For B4⊂Rn,n≥1,let A,Λ,λ,φbe as above,for someα>0,and let u∈H1(B4,RN),N≥1,be a solution to(2.1).ThenMoreover,the modulus of continuity of∇u in B1can be controlled in terms of

Remark 2.1Assumption(1.3)is weaker than A being Dini-continuous.

Remark 2.2The conclusion of Theorem 2.1 still holds(the dependence on α,andis changed accordingly),if{hi}∈ Lp(B4)for some p>n,and f satisfies

Remark 2.3This note was written in 2008.It was intended to be published after having an answer to the question raised above.

Theorem 2.1 follows from the following two propositions.

Proposition 2.1For,letΛ,λ,N be as above,and let A satisfy(1.1)–(1.2),and

for some non-negative functionφon(0,1)satisfying,for someµ>1,

Assume that h,f∈Cα(B4)for someα>0,and u∈H1(B4,RN)is a solution to(2.1).Then there exist a∈R and b∈Rn,such that

Then u,after changing its values on a zero Lebesgue measure set,belongs to,with u≡a and∇u≡b.Moreover,for some dimensional constant C,

Similar results hold for Dirichlet problem:LetΩ⊂Rn(n≥1)be a domain with smooth boundary,letΛandλbe positive constants,and let A satisfy,for N≥1,

where

Consider

Theorem 2.2(see[4])Assume the above,and let h,and g ∈ C1,α(∂Ω)for someα >0.Then an H1(Ω,RN)solution u to the above Dirichlet problem is in

Our proof of Proposition 2.1,based on the general perturbation in Lemma 3.1 in[5],is similar to that of Proposition 4.1 in[5].

Proof of Proposition 2.2For anywe see from(2.5)that as r→0,

Thus,by a theorem of Lebesgue,a=u a.e.in B1.We now take u≡a,after changing the values of u on a zero measure set.Letsatisfy,for some positive integer k,By(2.5),we have,for some dimensional constant C,

Switching the roles ofandleads to

Thus,by the above two inequalities and the triangle inequality,

The conclusion of Proposition 2.2 follows from(2.7)–(2.8).

We will findsuch that for all k≥0,

An easy consequence of(2.10)is

Here and in the following,C,C′and ϵ0denote various universal constants.In particular,they are independent of k.C will be chosen first and will be large,then C′(much larger than C),and finally ϵ0∈(0,1)(much smaller than

By Lemma 3.1 in[5],we can findsuch that

So

We have verified(2.9)–(2.12)for k=0.Suppose that(2.9)–(2.12)hold up to k(k ≥ 0).We will prove them for k+1.Let

Then W satisfies

A simple calculation yields,using(2.3),

By the induction hypothesis(see(2.10)–(2.12)),

By Lemma 3.1 in[5],there existssuch that

and,for some universal constantγ>0,

Let

A change of variables in(2.14)and in the equation of vk+1yields(2.9)and(2.12)for k+1.It follows from the above that

Estimates(2.10)for k+1 follow from the above estimates for vk+1.We have,thus,established(2.9)–(2.12)for all k.

For,using(2.10)–(2.11),(2.13),(2.3)and Taylor expansion,

We then derive from(2.12)and the above,using Hölder inequality,that,for some δ(r)= ◦(1)(asdepending only on φ,n,λ,Λ,N,µ,

Proof of Theorem 2.1Fix aon B3,and let

It is easy to see that for some µ>1,φsatis fies(2.3).Indeed,since it is easily seen that

the second inequality follows.For the first inequality,we only need to show that φ(2r)≤C(n)φ(r),since the rest is obvious.For anyletsatisfy

Since

we have

Thusφ(2r)≤ C(n)φ(r).

For any

Thus Theorem 2.1 follows from Propositions 2.1–2.2.

[1]Brezis,H.,On a conjecture of J.Serrin,Rend.Lincei Mat.Appl.,19,2008,335–338.

[2]Brezis,H.,A.Ancona:Elliptic operators,conormal derivatives and positive parts of functions,with an appendix by Haim Brezis,J.Funct.Anal.,257,2009,2124–2158.

[3]Jin,T.L.,Vladimir Maz’ya and Jean Van Schaftingen,Pathological solutions to elliptic problems in divergence form with continuous coefficients,C.R.Math.Acad.Sci.Paris,347(13–14),2009,773–778.

[4]Li,Y.Y.,Boundary C1regularity of solutions to divergence form elliptic systems with Dini-continuous coefficients,in preparation.

[5]Li,Y.Y.and Nirenberg,L.,Estimates for elliptic systems from composite material,Comm.Pure Appl.Math.,56,2003,892–925.

[6]Lieberman,G.,Hölder continuity of the gradient of solutions of uniformly parabolic equations with conormal boundary conditions,Ann.Mat.Pura Appl.,148,1987,77–99.