Asymptotics and Blow-up for M ass Critical Nonlinear Disp ersive Equations∗

Frank MERLE

(Dedicated to Professor Haïm Brezis on the occasion of his 70th birthday)

1 General Setting and Universality Questions

Nonlinear partial differential equations with Hamiltonian structure appear in models of wave propagation in physics or geometry.In the 1980s,basic properties of these equations were established,notably the existence and stability of special solutions called solitons.In the 1990s,tools from harmonic analysis led to a refined understanding of properties of the corresponding linear equations and how to extend these properties to nonlinear equations.In particular,the notion of criticality appeared.There remained the problem of understanding the dynamics related to nonlinear objects(or special solutions).These questions have attracted considerable interest in the last fifteen years,and yet we are just beginning to have a rough picture of the subject.More precisely,the questions are what to expect in this context,what can be proved,and with which patterns or tools can one approach these problems.In this paper,I will consider the following equations(see[34]for a more extend review on the subject).

(1)The L2(mass)critical nonlinear Schrödinger(cNLS for short)equation

(2)The L2(mass)critical Korteweg-de Vries(cKdV for short)equation

These are special cases of the nonlinear Schrödinger(NLS for short)equation and the generalized Korteweg-de Vries(gKd V for short)equation with power nonlinearities:

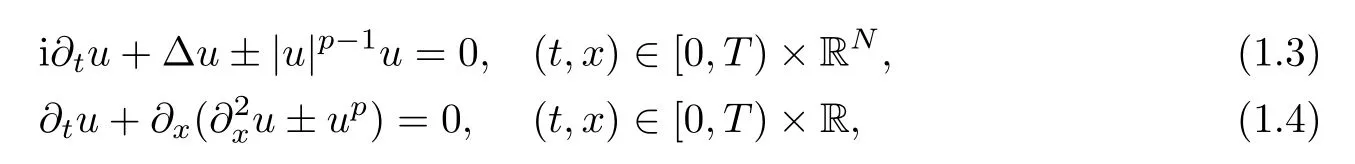
where the equation with a−sign in front of the nonlinear term is called defocusing and is expected to have only linear behavior,while the equation with a+sign is called focusing and is expected to have nonlinear behavior(the nonlinear effect balances the linear effect).

1.1 Local Cauchy theory

Given initial data at time t=0,the general problem is to understand the behavior of the solution u(t)for t>0(and t<0).First,in the 1980sand 1990s,the existence and uniqueness of local solutions in time were clarified using Strichartz estimates on the linear equation,and fixed point arguments to treat the nonlinear term in a perturbative way.Many authors contributed to these developments;pioneering works are[2,5–6,8,11–13],and many others.For the above equations,we have the following results.

The mass critical nonlinear Schrödinger(cNLS for short)equation and the mass critical Korteweg-de Vries(cKd V for short)equation are both locally well-posed(exhibiting existence and uniqueness of a maximal solution)on[0,T)(similarly onandwhereEither T=+∞ (and the solution is to said to be global),or T<+∞,and then if(the solution is said to blow up in finite time).Note that the value of T is in fact independent of the space,and in L2the blow-up criterion is given by a Strichartz norm(see[5,13]).Moreover,one has the following conservation laws(mass and energy):For all t∈[0,T),

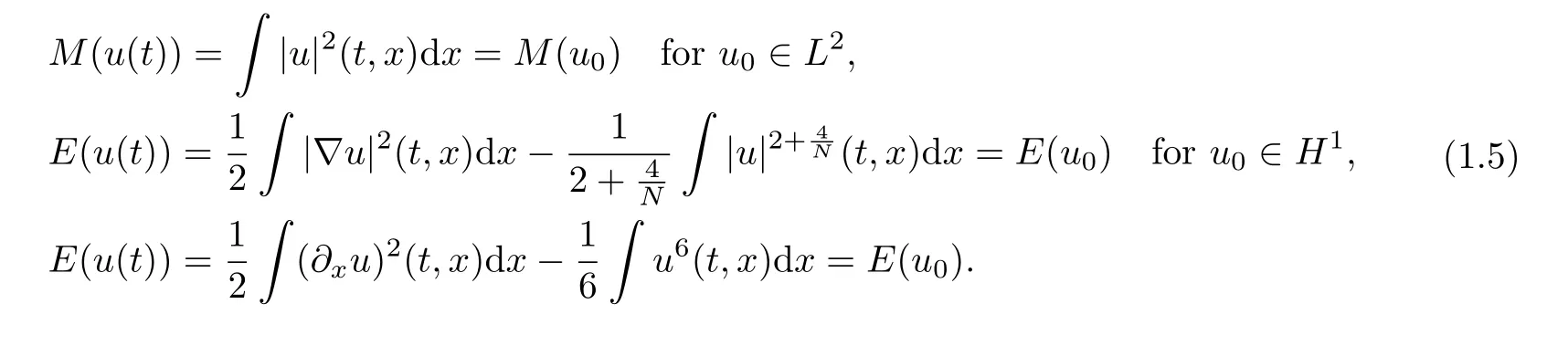
We have,in addition to the standard invariance by translation in space and time of the equation(with phase and Galilean invariance for the NLS equation),the scaling symmetry of the solution:If u(t,x)is a solution of cNLSequation,then forλ>0,

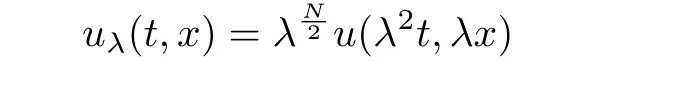
is also a solution,and for solutions of cKd V equation,

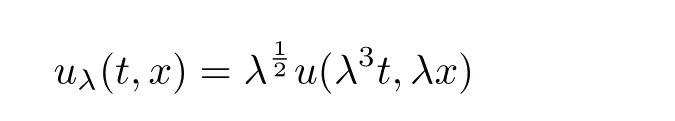
is also a solution.These transformations leave invariant the L2norm of the solution,so that both problems are called mass critical.In the defocusing case,the−sign in the energy becomes a+sign and the energy is coercive.

1.2 The problem of asymptotic behavior

We first have the following classical examples:

(i)Small data result.If the solution is small in the critical space(with a constant depending on a Strichartz inequality),then the solution is global and scatters(has linear behavior)as time approaches infinity.Let S(t)v0and S(t)(v0,v1)be the solutions of the corresponding linear equations.

There is aδ>0,such that in the case of cNLS and cKd V equations,ifthen the solution is global and there are v±∈ L2such that

(ii)Nonlinear objects such as periodic-in-time or stationary solutions.In the focusing situation,we have simple nonlinear objects which are stationary solutions up to the invariance of the equation.More precisely,we have for the cKd V equation a traveling wave solution of the form u(t,x)=Q(x−t)where Q is the one-dimensional solution in H1of

For the cNLS equation,the periodic solution is of the formwhere Q is the ground state solution in H1of

(see[1];note that excited states may also be considered).

(iii)The so-called self-similar solution.This is an expected typical example of blow-up solutions.We consider solutions of the form(up to some time-dependent translation and phase)for the mass critical KdV and cKdV equations,

for the mass critical NLS(the cNLSequation),

From the criticality and the conservation laws,for cNLS,cKdV equations,we will exclude such self-similar blow-up(in a more general form)for solutions in the critical space.Nonexistence of self-similar blow-up(in critical space)is one of the features of critical equations.Indeed,one can see that F satisfies an equation and that the behavior of the solution as the space variable goes to infinity shows that the solution is not in the critical space.To exclude self-similar-like behavior is in general a challenge deeply related to the nature of each equation.It corresponds to replacing an ordinary differential equation analysis by a partial differential equation analysis.

Other examples of solutions are generally in some respects a combination of the previous examples.They involve understanding the nature of dispersion at infinity in space and its coupling with the nonlinear dynamics.In particular,to construct a blow-up solution with a precise behavior is extremely complicated,even at a formal level,involving interaction of nonlinear/linear dynamics.Typically,dynamics of the solution is(up to scaling)asymptotic to a simple nonlinear object as defined before.In the global case,it is an example of asymptotic stability.In the blow-up case,we obtain a bubbling solution with a universal profile.In the examples considered,dynamics near a soliton are quite degenerate(having more degenerate directions than those given by the symmetries of the equation)and small perturbations in a regular space can dramatically change the global nonlinear behavior.In particular,behavior of initial data at infinity(tails)is essential.To get a formal understanding of these dynamics and to rigorously establish the formal picture was a challenge and required a new set of ideas.In general,understanding these interactions will lead to a classification of the possible dynamics.The two main problems of this type that we considered were to understand blow-up behavior for the mass critical NLS,and to prove blow-up for the the mass critical Kd V.These questions were open for several decades,and their resolution has a number of consequences in different contexts.Our strategy is to see that in each situation deep knowledge of the dispersion is related to a monotonicity formula(or sets of monotonicity formulas)which encodes notions of irreversibility.Note that when we speak about monotonicity formulas in these problems of time oscillatory integrals,we mean to have a decreasing quantity up to terms of lower order which are controlled.As we shall see,this monotonicity gives stability properties of the resulting dynamics.

We will now restrict attention to the physically relevant space dimension associated with each model.This is dimension one for the mass critical KdV(the cKdV equation),dimension two for the mass critical NLS(the cNLSequation).

2 The Nonlinear Schrödinger Equation

2.1 History of the problem

We focus in this section on the cNLS equation in the physically relevant dimension N=2.We will work in the energy space,assuming that u0∈H1.From an obstructive identity related to a pseudo-conformal invariance,it is known since the 1970s(see[10])that if

Variational arguments yield that blow-up is related to bubbling(and no blow-up occurs forThen in the early 1990s,the following precursor result containing a rigidity notion for Hamiltonian dynamics was proved.

Theorem 2.1(Dynamical Characterization of S in(2.2)and Q in(1.8))(see[30,32])Letand u(t,x)be the solution of the cNLS equation with initial data u0,then either(1)or(2)holds as follows:

(1)u is equal to S or to Q(x)eit,up to the symmetries of the equation,

(2)u is global,and scatters as

The first step of the proof is to show,using the minimality of the mass,that the solution is either scattering or nondispersive.Then variational arguments,estimates on tails,and conformal invariance lead to the result.Now the solutions S,Q can be seen as the only solutions which have a nonlinear dynamics at the critical mass level|Q|L2.

The next challenge is then to understand the dynamics in the context of a nonlinear/linear interaction,and a natural setting for this is small nonlinear data theory:For a small 0<α∗≪1 and u0∈H1with small supercritical mass

2.2 Loglog blow-up and classification(the Merle-Raphaël theory)

The starting point of this program is the Martel-Merle theory introducing rigidity notions for general data and dynamical application of these(see next section).We are now considering dynamics close to Q up to renormalization.Here the linearized problem around Q is very degenerate(having a higher degree of degeneracy than invariances of the equation)and the picture even at the formal level is not given by the linear theory.

The idea is the following:We consider,near Q,a family of nonlinear objects related to self-similar blow-up with a small time-dependent parameter b(t)(on bounded sets,these self similar solutions look like Q,but have a tail at infinity and thus fail(just barely)to belong to L2).Next,we consider Qb,a regularization at infinity of this family which is minimal in some sense.At this point,the idea is to find irreversibility through the time evolution of the parameter b(t)from a monotonicity formula in b(t)(recall that this problem originally involves oscillatory integrals in time).

The algebra related to Qbgives a formal proof of the loglog rate(related to cancellations at any polynomial order in the equation of the parameter b(t)).These notions based on monotonicity formulas do yield a rigorous proof of stable blow-up.The remarkable fact is that this theory works in H1and leads finally to the following theorem including a classification result.

Theorem 2.2(L2Critical Blow-Up)(see[7,35–39,45])Let u0∈ H1with small supercritical mass(2.3)and u∈C([0,T),H1)be the corresponding solution to the cNLS equation.Then:

(i)Sufficient condition for loglog blow-up:If E(u0)<0,or E(u0)=0 and,then u blows up in finite time with the loglog speed

(ii)Stability of loglog blow-up:The set of H1initial data u0such that u(t)blows up in finite time with the loglog law(2.4)is open in H1.

(iii)Universality of the bubble profile and classification of the blow-up rate:If T<+∞,then there exist parameters(λ(t),x(t),γ(t))and u∗∈ L2,such that

where Q is defined inandwhenand the speed of blow-up either satisfies the loglog law(2.4)or is bounded from below by the pseudo-conformal speed:

2.3 Threshold solutions

Theorem 2.2 yields the existence of an H1-open set of loglog blow-up solutions.In the neighborhood of Q,there are at least two other regimes:Scattering solutions displaying an H1-stable dynamics,and the solutions constructed by Bourgain-Wang[3]and Krieger-Schlag[17]which scatter to S:

and which saturate the upper bound(2.6):when t→0.

Such solutions are constructed by canceling interactions between S(t)and u∗,taking u∗to be very flat near the zero.Therefore,instability of such a solution is expected.In[40],adapting monotonicity properties to a mass constraint,one sees that the solutions(2.7)have an unstable threshold dynamics.

Theorem 2.3(Instability of S-Type Solutions(2.7))(see[40])The Bourgain-Wang solutions are the threshold dynamics for the cNLSequation and lie on the boundary of both H1-open sets of solutions which scatter linearly as time goes to infinity,and solutions which blow up in finite time in the loglog regime.

2.4 Other applications of this approach

There are spectacular applications of this approach to the construction of blow-up solutions with a given behavior.This point of view involving monotonicity properties in problems of oscillatory integrals has been successfully used to solve some classical critical problems.

The first step is to perform a formal analysis,where one considers specific localization of a self-similar profile(or its development with respect to a small parameter)and obtains,by computing the nonlinear equation of this reduction,a nonlinear finite-dimensional reduction of the problem.In all cases,we obtain the derivation of a monotonicity formula in a specific regime which ultimately leads to a rigor ousproof of the dynamics.It also shows that the infinite dimensional part of the solution is controlled by the finite-dimensional parameters.Here,in most cases,we use high regularity theory to obtain such monotonicity formulas via specific properties of the equation considered.A byproduct of the proof is a stability property with respect to the initial data of the dynamics in this higher regularity space(where one has the monotonicity formula).

At this level,general classification is still out of reach and is a real challenge in most cases.Let me cite a few of these problems(see[46]for more details or examples).We have the focusing energy critical wave and Schrödinger equations in dimension three(or their geometric counterparts in the critical dimension two)which can be reduced in the case of symmetry to the following equation:

(i)The wave maps into the sphere S2(see[18,47–49])

我打电话给黄玲说自己要到外地出差，问她大概什么时候回来，也许等她回来我可以将钥匙交到她手里。我不知道为什么她要将钥匙交给我，难道我这个只认识几个月的女人比她的男朋友还可靠？黄玲给我的疑问太多，她像是藏在墨镜背后的一个神秘的女人，时而近在咫尺温暖人心，时而遥不可及神秘难测。

(ii)The Schrödinger maps into the sphere S2(see[41])

3 Generalized Korteweg-de Vries Equation

The cKd V equation admits the same conservation laws and scaling invariance as the cNLS equation and is mass critical.The problem of blow-up for the cKd V equation was considered as a classical and natural question,since it has the same features as the mass critical NLSequation but no conformal invariance(or associated virial identity which leads to a simple obstruction argument to global existence).For small 0<α∗≪1,we consider data such that

3.1 Subcritical and critical Martel-Merle theory for the generalized K orteweg-de Vries equation

This problem was thoroughly studied by Martel and Merle in the early 2000s.Following the dynamical characterization of S for the mass critical NLS equation,where the nondispersive character of solutions follows from the mass constraint of the initial data,and the work of Glangetas,Merle[9],where for general data a minimality of an asymptotic dynamical property shows the nondispersive character of solutions,the set of results presented in this subsection is the next major breakthrough in the application of the notion of nondispersive solutions.

The idea is to find a contradiction from energy constraints(E(u0)<0)and the exact asymptotic behavior of the solution in the critical situation.For this purpose,a method was introduced to produce irreversibility and rigidity in the problem.This method has as a byproduct the spectacular application in the subcritical case where solitons are stable(up to symmetry).Let us start with the simpler configuration.

(i)The subcritical case(1

In this subsection,we consider(1.4)for 10,

is also a solution,whereThe main question was the asymptotic stability of the soliton Q:For initial data u0initially close to Q in the energy space,does the solution centered at a suitably chosen x(t)converge to Qclocally in space,as time goes to infinity?The main approach is to introduce rigidity,breaking the reversibility of the equation.For this purpose,we consider a new entire solution v(t)with initial data asymptotic to u(tn,xn+·)locally in space for some xn,where tngoes to infinity as follows:

Then from a family of monotonicity formulas of the mass on half-lines,we are able to break the reversible character of the solution v(t)and to prove elliptic exponential estimates in x,uniform in time,on v(t,x+y(t))for some y(t).Thus v(t)is a nondispersive solution of the equation and we are able to conclude using dispersive properties that v(t,x)is exactly Q(x−t)up to symmetry of the equation.

Theorem 3.1(Asymptotic Stability of Q)(see[22]) Assume 1

where Qc+is defined in(3.2).

(ii)The critical case(p=5).

The situation in the critical case is much more delicate than in the subcritical case because of the possible oscillation in time of the scaling of the soliton.Nevertheless,through a use of irreversibility we are able to prove in the energy space the following.

Theorem 3.2(L2Critical Blow-Up for the Kd V Equation)(see[22,23–25,33]) Let u0∈H1satisfying(3.1)and u∈C([0,T),H1)be the corresponding solution of the cKdV equation.Then:

(i)Negative energy gives blow-up:If the initial data is such that E(u0)<0,then the solution blows up with T finite or infinite

(ii)No self-similar blow-up:There are no solutions such that T<+∞and

(iii)Universality of the bubble of concentration:There exist(λ(t),x(t))such that,for A>0,

wherewhen t→ T.

We remark that blow-up is in fact a consequence of asymptotic stability and energy constraints.Let E(u0)<0.The proof of blow-up goes along the following lines(arguing by contradiction):If the solution does not blow up,we are able to prove that u(tn)satisfies(3.5)with a sequenceλ(tn)>c>0.Using E(Qc)=0 and the coercivity of the energy for small mass,we obtain that the energy computed on this time sequence E(u(tn))is positive,which contradicts the conservation of the energy.

3.2 Critical Martel-Merle-Raphaël theory

Another piece of Martel-Merle theory is as follows:Space decay of the initial data with negative energy leads to blow-up in finite time.Moreover,an estimate on the blow-up rate was obtained(see[25]).But clearly,compared to the mass critical NLS equation,one piece is missing in the full description of the blow-up.

Recently,we came back to this problem and achieved a much more ambitious goal:We were ableto completely understand all solutions and their asymptotics for initial data near the ground state with decay(including blow-up rate/stability/instability/universality questions).This was set forth in the series of papers[27–29].Finally,we end up with a complete nonlinear finite dimensional description of the dynamical picture(despite the high degeneracy of the equation near the ground state).This is the only such situation known in the literature.The expectation is that the picture obtained is canonical and should be extended to different contexts.

More precisely,consider the set of initial data forα0small,

and consider the L2neighborhood around the family of solitary waves

One first has the rigidity of the dynamics for data in A.

Theorem 3.3(Rigidity of the Flow in A(3.6))(see[27])Letand u0∈ A⊂Tα∗.Let u∈C([0,T),H1)be the corresponding solution of the cKdV equation.Then one of the following three scenarios occurs:

(Blow-up)The solution blows up in finite time T>0 with the universal regime

(Soliton)The solution is global(T=+∞)and converges asymptotically to a solitary wave Q c(u0).

(Exit)The solution leaves the tube Tα∗ (3.7)at some time 0

Moreover,the scenarios(Blow-up)and(Exit)are stable under small perturbations of the initial data in A.

This is a complete classification of solutions with data in A which remain close in the L2sense to the manifold of solitary waves.Again,a monotonicity formula(not in the energy space but in a norm related to A)is a crucial step is this result.As for the cNLS equation,we have the following dynamical characterization of Q(1.8):If E(u0)≤ 0,u0∈ A andthen u blows up in finite time on both sides in time with the blow-up law(3.8).

It remains to understand the long-time dynamics in the(Exit)regime.The first step is the existence and uniqueness of a minimal blow-up element which is the generalization of the S(t)dynamics for the cNLS equation.This result is a surprise since it was thought to be specific to the mass critical NLSequation and linked to the conformal invariance.A key to this existence result is the above classification result on localized initial data(even if this special solution has a spatially slow decay at infinity),and for the uniqueness a set of monotonicity properties.

Theorem 3.4(Existence and Uniqueness of the Minimal Mass Blow-Up Element)(see[28])There exists a unique solution(up to symmetries of the equation)in H1of the cKdV equation with minimal masswhich blows up at T=0.

Moreover,is globally defined for positive time.

We next prove the relevance of this unstable solutionand the classification at minimal mass through a result which linksto a stable scenario(see also special examples of this fact in[32,40]for the mass critical NLS equation,and for the critical wave equation in[43],where they obtained a related classification of the flow near the solitary wave involving a description of the scattering zone and its boundary through a non-return lemma).The solutionis the universal attractor of all solutions in the(Exit)regime.

Proposition 3.1(Description of the(Exit)Scenario)(see[28])Let u(t)be a solution in the(Exit)scenario of Theorem 3.3 and let t∗be the corresponding exit time.

(i)Then there existτ∗= τ∗(α∗)and(λ∗,x∗)such that

(ii)Assume that the solutionscatters asthen any solution in the(Exit)scenario is global for positive time and scatters as

Note that it is natural to expectto scatter asfrom the situation for cNLS and ecNLW equations(see below)where it is proved.

It is important to notice that the above results rely on the explicit computation on some parametrization of the solution for initial data in A,and not on algebraic virial type identities.One may justify the following procedure:Introduce the nonlinear decomposition of the flow

whereϵis small,and show that to leading order,λ(t)obeys the dynamical system

The three regimes(Exit),(Blow-up),and(Soliton)now correspond at the formal level respectively toλt(0)>0,λt(0)<0,and λt(0)=0.The main and deep part is a monotonicity formula in the original variable.

We now consider initial data with slowly decaying tails interacting with the solitary wave which lead to new exotic singular regimes.

Proposition 3.2(Exotic Blow-up Regimes for the cKd V Equation)(see[29]) There are solutions u∈H1of the cKdV equation,with initial data arbitrarily close in H1to Q,

(i)which blow up at t=0 with speed

(ii)which blow up at+∞ withas t→ +∞,forν>0.

This shows that universality is lost without decay of the initial dataIn particular,the H1Martel-Merle theory is still relevant and optimal for solutions only in the energy space without strong decay.

[1]Berestycki,H.and Lions,P.-L.,Nonlinear scalar field equations I:Existence of a ground state,Arch.Rational Mech.Anal.,82,1983,313–345.

[2]Bourgain,J.,Global well-posedness of defocusing critical nonlinear Schrödinger equation in the radial case,J.Am.Math.Soc.,12,1999,145–171.

[3]Bourgain,J.and Wang,W.,Construction of blowup solutions for the nonlinear Schrödinger equation with critical nonlinearity,Ann.S.Nor.Pisa,25,1998,197–215.

[4]Brezis,H.and Coron,J.M.,Convergence of solutions of H-systems or how to blow bubbles,Arch.Rational Mech.Anal.,89,1985,21–56.

[5]Cazenave,T.and Weissler,F.,Some remarks on the nonlinear Schrödinger equation in the critical case,Nonlinear semigroups,partial differential equations and attractors,18–29,Lecture Notes in Math.,1394,Springer,Berlin,1989.

[6]Colliander,J.,Keel,M.,Staffilani,G.,et al.,Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in R3,Ann.of Math.,167,2008,767–865.

[7]Fibich,G.,Merle,F.and Raphaël,P.,Proof of a spectral property related to the singularity formation for the critical NLS,Phys.D,220,2006,1–13.

[8]Ginibre,J.and Velo,G.,Generalized Strichartz inequalities for the wave equation,J.Funct.Anal.,133,1995,50–68.

[9]Glangetas,L.and Merle,F.,A Geometrical Approach of Existence of Blow-up Solution in H1for Nonlinear Schrödinger Equations,Publications du Laboratoire d’Analyse Numérique,Université Pierre et Marie Curie,1995.

[10]Glassey,R.,On the blowing up of solutions to the Cauchy problem for nonlinear Schrödinger equations,J.Math.Phys.,18,1977,1794–1797.

[11]Kato,T.,On nonlinear Schrödinger equations,Ann.Inst.H.Poincaré Phys.Théor.,46,1987,113–129.

[12]Kenig,C.,Recent developments on the global behavior to critical nonlinear dispersive equations,Proceedings of the International Congress of Mathematicians,Volume I,326–338,Hindustan Book Agency,New Delhi,2010.

[13]Kenig,C.,Ponce,G.and Vega,L.,Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle,Comm.Pure Appl.Math.,46,1993,527–620.

[14]Killip,R.,Tao,T.and Visan,M.,The cubic nonlinear Schrödinger equation in two dimensions with radial data,J.Eur.Math.Soc.,11,2009,1203–1258.

[15]Killip,R.and Visan,M.,The focusing energy-critical nonlinear Schrödinger equation in dimensions five and higher,Amer.J.Math.,132,2010,361–424.

[16]Krieger,J.,Nakanishi,K.and Schlag,W.,Global dynamics away from the ground state for the energycritical nonlinear wave equation,Math.Z.,272,2012,297–316.

[17]Krieger,J.and Schlag,W.,Non-generic blow-up solutions for the critical focusing NLSin 1-D,Jour.Eur.Math.Soc.,11,2009,1–125.

[18]Krieger,J.,Schlag,W.and Tataru,D.,Renormalization and blow-up for charge one equivariant critical wave maps,Invent.Math.,171,2008,543–615.

[19]Krieger,J.,Schlag,W.and Tataru,D.,Slow blow-up solutions for the H1(R3)critical focusing semilinear wave equation,Duke Math.J.,147,2009,1–53.

[20]Landman,M.J.,Papanicolaou,G.C.,Sulem,C.and Sulem,P.-L.,Rate of blowup for solutions of the nonlinear Schrödinger equation at critical dimension,Phys.Rev.A,38,1988,3837–3843.

[21]Lions,P.-L.,The concentration-compactness principle in the calculus of variations:The limit case I and II,Rev.Mat.Ibero.,1,1985,45–121 and 145–201.

[22]Martel,Y.and Merle,F.,A Liouville theorem for the critical generalized Korteweg–de Vries equation,J.Math.Pures Appl.,79,2000,339–425.

[23]Martel,Y.and Merle,F.,Instability of solitons for the critical generalized Korteweg–de Vries equation,Geom.Funct.Anal.,11,2001,74–123.

[24]Martel,Y.and Merle,F.,Stability of blow-up profile and lower bounds for blow-up rate for the critical generalized Kd V equation,Ann.of Math.,155,2002,235–280.

[25]Martel,Y.and Merle,F.,Blow-up in finite time and dynamics of blow-up solutions for the L2-critical generalized Kd V equation,J.Amer.Math.Soc.,15,2002,617–664.

[26]Martel,Y.and Merle,F.,Nonexistence of blow-up solution with minimal L2-mass for the critical gKd V equation,Duke Math.J.,115,2002,385–408.

[27]Martel,Y.,Merle,F.and Raphaël,P.,Blow-up for critical gKd V equation I:Dynamics near the soliton,Acta Math.,to appear.ar Xiv:1204.4625

[28]Martel,Y.,Merle,F.and Raphaël,P.,Blow-up for critical gKd V equation II:Minimal mass solution,J.E.M.S.,to appear.

[29]Martel,Y.,Merle,F.and Raphaël,P.,Blow-up for critical gKd V equation III:Exotic regimes,Annali Scuola Norm.Sup.di Pisa,to appear.arXiv:1209.2510

[30]Merle,F.,Determination of blow-up solutions with minimal mass for nonlinear Schrödinger equations with critical power,Duke Math.J.,69,1993,427–454.

[31]Merle,F.,Construction of solutions with exactly k blow-up points for the Schrödinger equation with critical nonlinearity,Comm.Math.Phys.,129,1990,223–240.

[32]Merle,F.,On uniqueness and continuation properties after blow-up time of self-similar solutions of nonlinear Schrödinger equation with critical exponent and critical mass,Comm.Pure Appl.Math.,45,1992,203–254.

[33]Merle,F.,Existence of blow-up solutions in the energy space for the critical generalized Kd V equation,J.Amer.Math.Soc.,14,2001,555–578.

[34]Merle,F.,Asymptotics for critical nonlinear dispersive equations,Proceedings of the International Congress of Mathematicians,2014,to appear.

[35]Merle,F.and Raphaël,P.,Sharp upper bound on the blow-up rate for the critical nonlinear Schrödinger equation,Geom.Func.Anal.,13,2003,591–642.

[36]Merle,F.and Raphaël,P.,On universality of blow-up profile for L2critical nonlinear Schrödinger equation,Invent.Math.,156,2004,565–672.

[37]Merle,F.and Raphaël,P.,The blow-up dynamics and upper bound on the blow-up rate for the critical nonlinear Schrödinger equation,Ann.of Math.,161,2005,157–222.

[38]Merle,F.and Raphaël,P.,Profiles and quantization of the blow-up mass for critical nonlinear Schrödinger equation,Commun.Math.Phys.,253,2005,675–704.

[39]Merle,F.and Raphaël,P.,On a sharp lower bound on the blow-up rate for the L2critical nonlinear Schrödinger equation,J.Amer.Math.Soc.,19,2006,37–90.

[40]Merle,F.,Raphaël,P.and Szeftel,J.,The instability of Bourgain-Wang solutions for the L2critical NLS,Amer.Jour.Math.,135,2013,967–1017.

[41]Merle,F.,Raphaël,P.and Rodnianski,I.,Blow-up dynamics for smooth data equivariant solutions to the energy critical Schrödinger map problem,Invent.Math.,193,2013,249–365.

[42]Merle,F.,Raphaël,P.and Rodnianski,I.,Type II blow up for the energy supercritical NLS,preprint.

[43]Nakanishi,K.and Schlag,W.,Global dynamics above the ground state energy for the cubic NLSequation in 3D,Arch.Ration.Mech.Anal.,203,2012,809–851.

[44]Perelman,G.,On the formation of singularities in solutions of the critical nonlinear Schrödinger equation,Ann.Henri Poincaré,2,2001,605–673.

[45]Raphaël,P.,Stability of the log-log bound for blow-up solutions to the critical nonlinear Schrödinger equation,Math.Ann.,331,2005,577–609.

[46]Raphaël,P.,Blow up bubbles in Hamiltonian evolution equations:A quantitative approach,Proceedings of the International Congress of Mathematicians,2014,to appear.

[47]Raphaël,P.and Rodnianski,I.,Stable blow-up dynamics for the critical co-rotational wave maps and equivariant Yang-Mills problems,Publ.Math.Inst.Hautes Etudes Sci.,115,2012,1–122.

[48]Rodnianski,I.and Sterbenz,J.,On the formation of singularities in the critical O(3)σ-model,Ann.of Math.,172,2010,187–242.

[49]Sterbenz,J.and Tataru,D.,Regularity of wave-maps in dimension 2+1,Comm.Math.Phys.,298,2010,139–230.

[50]Tao,T.,Visan,M.and Zhang,X.,Minimal-mass blowup solutions of the mass-critical NLS,Forum Math.,20,2008,881–919.

[51]Weinstein,M.I.,Nonlinear Schrödinger equations and sharp interpolation estimates,Comm.Math.Phys.,87,1983,567–576.