Dijkstra最短路径算法的堆优化实验研究
张翰林,关爱薇,傅 珂,孙廷凯
(1. 南京理工大学 理学院,江苏 南京 210094;2. 南京理工大学 计算机科学与工程学院,江苏 南京 210094)
Dijkstra最短路径算法的堆优化实验研究
张翰林1,关爱薇1,傅 珂1,孙廷凯2
(1. 南京理工大学 理学院,江苏 南京 210094;2. 南京理工大学 计算机科学与工程学院,江苏 南京 210094)
Dijkstra最短路径算法是图论的经典算法。设有向图G有n个顶点和m条弧,则该算法的时间复杂度为Θ(m+n2)。前人的理论研究表明,若用二叉堆或d堆作为辅助数据结构,可不同程度地降低算法的时间复杂度。但是,这些研究给出的都是比较松弛的上界描述。本文设计了一系列实验,利用二叉堆和d堆实现了该算法的优化,并通过模型拟合回归的方式研究了优化算法的时间复杂度。我们发现,对于稠密图,采用二叉堆优化算法,实际的时间复杂度可降低为m和nlogn的线性函数;而采用d堆,时间复杂度可降低为m、ndlogdn、nlogdn、dlogdn和n的线性函数,其中的d值对复杂度有显著影响,变化趋势呈现某些共同特征,而最优d值位于[5,7]区间。
Dijkstra最短路径算法;二叉堆;d堆;时间复杂度
0 引言
1959年,狄克斯特拉(Edsgar Dijkstra)成功设计并实现了在有障碍物的两个地点之间找出一条最短路径的高效算法,这个算法被命名为“狄克斯特拉算法[1]”,解决了机器人学中的一个十分关键的问题,即运动路径规划问题,至今仍被广泛应用[2-6]。
最短路径不仅仅指地理意义上的距离最短,还可以引申到其他的度量,如时间、费用、容量、线路等。归结起来就是指由结点和路径组成的图中两结点之间的最短路径[7]。
最短路径问题一直是运筹学、计算机科学、地理信息科学、交通运输等领域的一个研究热点[5-9]。很多实际问题都可以通过抽象进而转化为网络中的最短路径计算问题,如道路交通网络中的出行路线选取问题,计算机网络中信息流在路由器间的最佳传输问题,以及社会关系网络中两个陌生人之间的联系紧密度计算问题等。因此,针对网络中最短路径的有效计算问题研究具有重要的理论和现实意义。
近年来伴随着大规模动态网络数据的出现,最短路径的实时计算面临着新一轮的挑战。很多实际系统(如GPS导航系统以及消防、救灾等应急系统)都要求在尽可能短的时间内获取最佳路径,以更好地应对网络动态等方面的影响,为用户提供快速决策。所有这些都依赖于更高性能的最短路径算法[6-9]。
堆是一种数据项按序排列的数据结构。在排序问题中[10-11],堆结构具有优良的时间复杂度。d-堆则是堆(二叉堆)的一个变形[10-11],比二叉堆更加灵活。如果用堆结构作为Dijkstra算法中的数据存储结构,该算法的时间复杂度将被优化。
在Dijkstra算法中,设有向图G有n个顶点和m条弧,使用邻接表作为图的存储结构,则该算法的时间复杂度为Θ(m+n2)[11]。而在实际工程计算中,n通常较大,Θ(n2)的算法复杂度较高,有较大的提升空间。可以证明,若用最小堆作为辅助数据结构,算法的复杂度可降低为O( mlogn)[11];若进一步用d堆(二分堆的推广)结构,精心选择合适的d值,对于稠密图,算法的复杂度可降低到O( m),即线性时间复杂度[11]。然而,上述理论分析得出的都是比较松弛的上界描述,实际上由于图结构的复杂性,算法的实际性能尚未可知,本项目将对这个问题进行研究和实现。
1 理论基础
1.1 传统算法
先介绍Dijkstra传统算法。
首先,我们有一个由节点和有向弧组成的有向图G,该图所有边(弧)的权值均非负。开始,我们将所有的节点划分为两个集合X和Y。初始时,X ={1}, Y = {2,3,4,…,n}。若x∈X,则表示由源点到x节点的最短路径已经被找到;Y则记录了剩余的节点(最短路径还没有被确定的节点)。Y中的每个节点y有一个对应的量λ[y],该值是从源节点到y (并且只经由X中的节点) 的最短路径值。
Dijkstra算法[11]:
1. 假设V={1,2,3,…,n}表示所有节点,且源点为1,则X←{1};Y←V-{1}。
2. 对于所有的y∈Y,若存在从1到y的边,则令λ[y]等于这条边的长度,否则令λ[y]=∞。
3. 选择一个λ[y]最小的顶点y∈Y,并将其移动到X 中。
4. 将Y中每个和y相邻的顶点w的λ[w]都重新计算并更新(表示经由y到w的一条更短的路径被发现)。
5. 若Y≠Ø,则回到第二步,否则算法结束。
在上述算法中,所有的结点被分为三种类型,即已标记节点(即集合X中的节点)、未标记节点(即集合Y中那些λ[y]=∞的节点)和临时标记节点(即集合Y中那些λ[y]为有限值的节点)。在上面的算法中,关键的是第3步,需要从临时标记节点中寻找λ[y]最小的节点。若将这些节点的权值λ [y]保存在数组、链表或者队列等线性结构中,每次查找最小值都需要用传统的遍历算法,则该步骤的时间复杂度为Θ(n2)。在第4步中,这个步骤恰好对每条边都检查一次,所以其时间复杂度为Θ(m)。因此该算法的时间复杂度为Θ(m+n2),对于m<nlogn的稀疏图,或者对于m≥nlogn的稠密图,算法的复杂度都可以表示为Θ(n2)。
1.2 二叉堆优化算法[11]
接下来介绍我们如何用堆(二叉堆)来优化Dijkstra算法。
1.2.1 堆优化动机
堆是一种特殊的完全二叉树,其中小顶堆具有这样的特点:父节点的键值不大于子节点的键值,堆的数组表示呈“基本有序”状态,堆顶元素永远是最小的。这样的特性刚好能满足这个算法的需求,所以,我们可以使用堆结构来优化Dijkstra算法。堆元素保存在形如H[1...n]的数组内,其中H[1]为堆的根。
1.2.2 堆排序算法在Dijkstra算法中的实现
先介绍上浮和下渗算法。
若某个节点H[i]键值小于其父节点的键值(或大于其儿子节点的键值),就违背了堆的特性,需要进行上浮(或下渗)调整。
调整方法为:
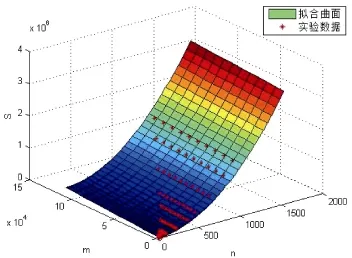
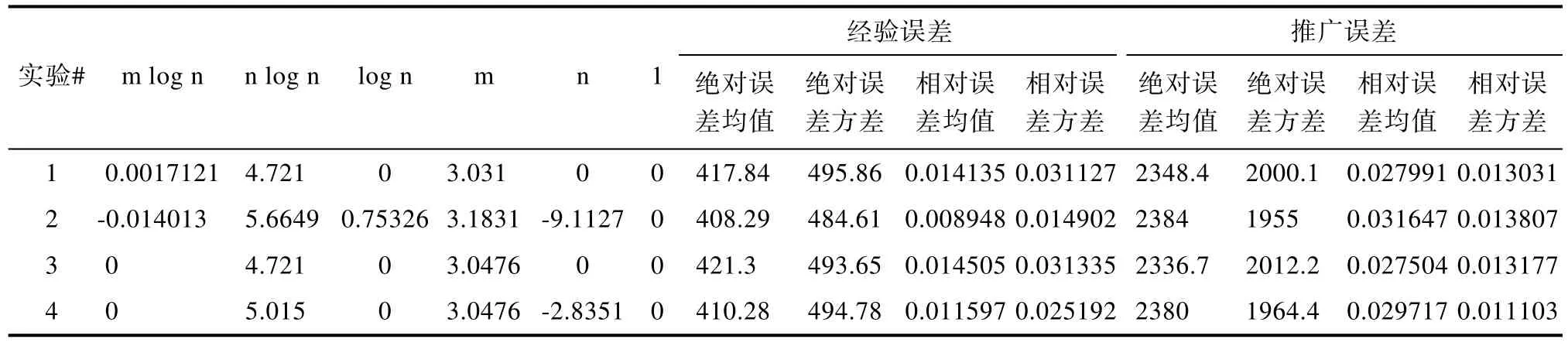
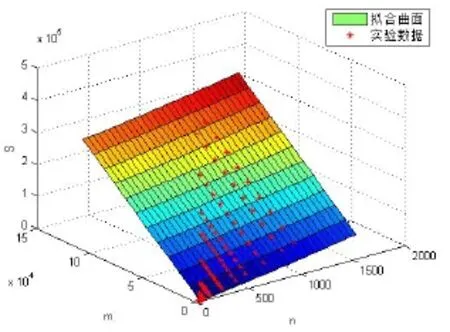
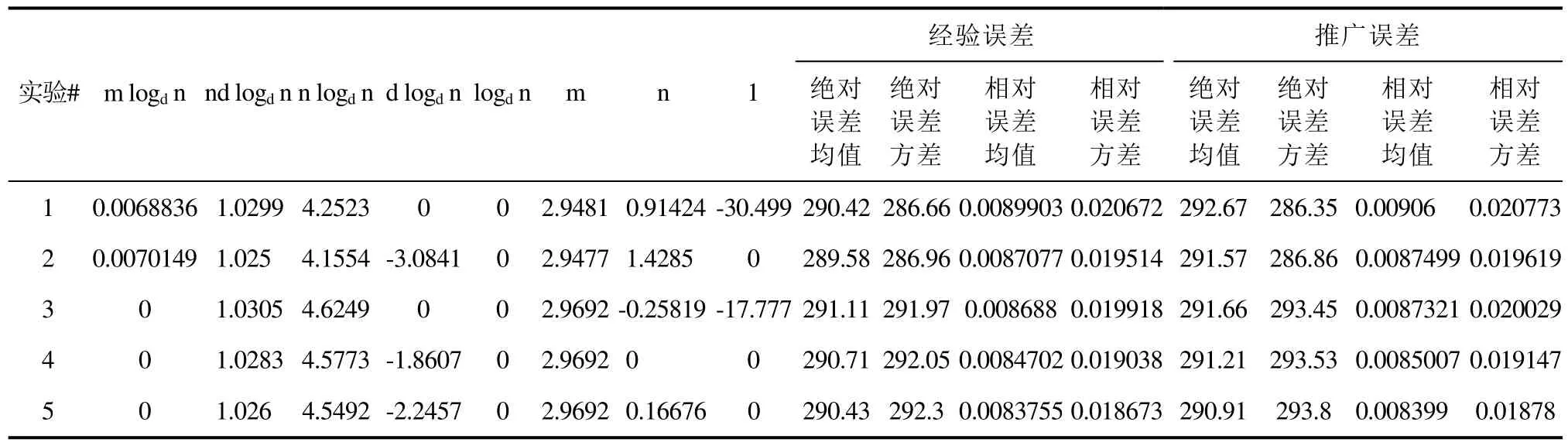
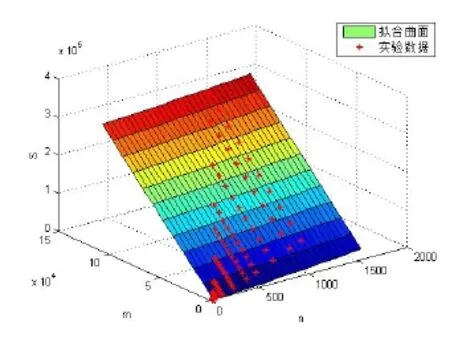
上浮:比较H[i]及其父节点H[i/2]的键值,若key(H[i]) 下渗:沿着从H[i]到子节点(可能不唯一,则取其键值较小者)的路径,比较H[i]与子节点的键值,若key(H[i])>min(H[2i], H[2i+1])则交换之。重复这一过程直到叶子节点或满足堆特性为止。 在Dijkstra算法中,我们需要修改节点键值、插入节点和删除节点这三种操作,他们均可用上浮和下渗两种算法完成。 修改节点键值:直接修改,然后根据需要对该节点进行上浮操作直到满足堆特性为止。 插入节点:将需插入的节点放在堆的最后一个位置,然后对该节点做上浮操作,直到满足堆特性为止。 删除堆顶节点:先用堆中最后一个节点取代H[1],然后对H[1]作下渗操作,直到满足堆特性为止。 1.2.3 堆排序算法在Dijkstra算法中的时间复杂度 1.3 d堆优化算法[11] d-堆(有的文献称为k叉堆)是一种新型的数据结构,d-堆与普通堆很类似,普通堆即二叉堆,但d-堆中的每个非叶结点有d个子女,而不是2个。 由这个特性知,高度为h的一个满的d叉堆的结点个数为dh-1;有n个元素的d叉堆高度为h=O(logdn),即:每次上浮操作耗时为O(logdn),下渗操作由于要和d个儿子进行比较,所以耗时为O( dlogdn)。如果我们用d-堆代替二叉堆来优化Dijkstra算法,显然时间复杂度将降为O( ndlogdn+ mlogdn)[11]。 进一步,对于稠密图(m≥n1+ε),如果我们选取d的值为,那么时间复杂度将变为 这证明,对于稠密图(m≥n1+ε),d堆优化的Dijkstra算法可将其时间复杂度进一步降至O( m/ε),即线性阶。 然而,这些堆优化分析得出的都是比较松弛的上界描述。在实际中,堆优化的效果究竟如何,优化后的算法复杂度是什么,还未可知。接下来,我们将用实验来探究。 2.1 传统算法 首先设计实验数据。图G须满足稠密图的条件,即顶点数n和边数m满足m≥nlogn。若取m=n1+(εε>0),则当n比较小时,ε需要取得很大,才能从数值上满足稠密图的要求m≥nlog n,不利于实验数据的选取。所以,我们取m=knlog(n k≥1),这样配置的图可以保证满足稠密图的要求m≥nlogn。然后,我们取顶点数n分别为32,64,128,256,400,512,700,900,1024。由于在图G中,m存在上界,即m≤(n-1)n,所以当n=32时,k可取1,2,3,4,5,6;当n≥64时,可取k=1,2,3…10。对于每种配置的(n,m),随机生成10个有向图,保存在邻接表内。接下来的所有实验中,我们将统一使用这组实验数据,以便进行算法之间的对比。 在使用原始Dijkstra算法编写的程序里加入计数器,分别记录判断、比较、赋值的次数。我们将使用判断、比较和赋值次数之和S来作为算法时间复杂度的表征,即S=T(m,n)。对于对于每种配置的(n,m),10个图数据运行的结果进行平均得到T( m, n)。记每个三元组(n, m, T( m, n))作为一组观察数据。 实验得到k组(n, m, T( m, n))数据,建立用m,n(和/或其对数形式)构造的多项式,例如T( m, n)= c n2+c n+c m+c的形式。假设我们找到一组参数 1234 ci,i=1,…4,我们希望对于每个参数配置(n,m),这个模型拟合得到的值恰好等于观察值T( m, n),即可以表示为形如Ax=b的线性方程组,其中:一般来说k>>4,例如这里k=9,得到的超定方程组Ax=b一般没有严格的代数解,为此我们使用最小二乘法,使得误差平方Ax-b2尽量小。在Matlab中,这样的解xˆ可以直接用xˆ=A b来计算。我们就可以构建根据需要构建各种不同的多项式模型,得到不同的参数向量解x,然后通过一定的评价方法对比研究这些模型的优劣(详见下文描述)。 我们以n2作为最高次项,运用Matlab对若干模型进行拟合,得到各项系数,并计算各模型的绝对误差和相对误差,对比得到相对较优的模型,最后分析结果。 从结果数据来看,原始算法的操作总数S主要受图的顶点数n影响,呈现二次函数关系,而与m的关系较小。 从回归分析的结果来看,无论是哪种以n2作为最高次项模型,拟合精度都非常高,绝对误差和相对误差都极小,各项系数大小也贴近实际,非常合理。斟酌之后,我们选择 S=1.5003n2+8.9329n+2.0028m+9.6572 作为最终的拟合模型。这个拟合结果与实际值的相对误差的绝对值,用平均值和均方差来表示就是0.00160±0.00325。其三维图像如图1所示: 图1 传统算法复杂度函数三维图Fig.1 Complexity Function of Traditional Algorithm 3-D Image 这是一个与理论分析完全一致的结果。这就验证了原始的Dijkstra算法的时间复杂度为O( n2)。 2.2 二叉堆优化算法 我们改写程序得到用二叉堆优化的Dijkstra算法程序,仍用相同的实验数据,用同样的方法运行程序,得到操作总数并绘制成表。 这次,我们将使用系统的误差分析方法,综合各个拟合模型的经验风险、推广性风险以及模型的复杂性来挑选合适的拟合模型。为了考察模型的泛化能力,对于每种配置(n,m),我们又随机生成了相同配置的另外10组图,用于测试模型的推广误差,把原先的实验结果称为b1,推广实验的结果称为b2,拟合模型的计算结果称为bˆ=Ax,那么经验误差是推广误差就是,一般情况下,我们用r1+λr2来衡量一个模型拟合的好坏,其中正则化参数λ代表推广误差和经验误差重要程度的比值,在本实验中,λ可取为1。我们还将模型的复杂程度作为一个标准,即在误差r1+λr2相当的情况下,挑选那些相对更简单光滑(即项数少、系数绝对值小)的模型作为最佳拟合模型。 我们以mlogn为最高次项,构建了可能包括nlogn、logn、m、n和常数项中的一项或若干项共25=32种所有形态的多项式模型,并进行最小二乘法拟合,计算和记录各拟合模型的经验误差和推广误差,分析结果数据,得到以下结论(由于表格过大,数据略): 二叉堆优化的Dijkstra算法的操作总数比起传统的算法要小很多,这证明二叉堆的存储结构确实优化了算法。从拟合结果的系数来看,最高次项mlog n前的系数并不统一,差别较大,对此我们得不到一个较好的结论。但如果从误差的角度来分析,我们观察若干个拟合精度较高的模型,它们有几个共同特点:最高次项mlogn前面的系数绝对值都非常接近于0,有正有负;均包含m项和nlogn项,而且m项和nlogn项前面的系数都很稳定。在这组实验中,我们根据拟合精度和模型复杂程度挑选出两个最优的模型来作比对(见表1的1、2号模型)。 于是我们考虑剔除mlogn这个“最高次项”,把m作为最高次项,考察了共24=16种形态的多项式,进行重新拟合。观察拟合结果,我们发现,拟合模型只要含有m项和nlogn项,就能得到误差小,系数稳定的拟合结果。我们同样择优选出两个模型来作比较(见表1的3、4号模型)。 表1 二叉堆优化算法模型比较Tab.l Binary Heap Optimization Algorithm Model Comparison Table 从此表中可以得出一个显而易见的结论:mlog n是一个可有可无的项,m和nlogn才是这个算法的最高次项。 综合经验误差与推广误差,同时为了追求模型的简单,我们选择3号模型。 S=3.0476m+4.721nlogn 作为最终的拟合模型,其三维图像如图2所示: 图2 二叉堆优化算法函数图像Fig.2 Binary Heap Optimization Algorithm Function Image 我们可以说,二叉堆优化的Dijkstra算法的时间复杂度实际上已经达到了用斐波那契堆进行优化的复杂度[9](log) O mnn+,实验可以佐证这一点。 对于这一现象,可以做出如下解释: 1. 首先,在这个算法中,如我们前面所说,插入堆操作共有(n-1)次,这个数字就是算法实际上执行的次数;更新操作最多有(m-n+1)次,但在实际的操作中,会有很多无需更新节点权值的时候(即新的权值大于当前权值),更新操作的实际执行次数远远达不到(m-n+1)这个上限。 2. 堆操作的时间复杂度被认为是(log)On。但实际上,堆的初始大小仅为源点s的邻接点个数,算法执行过程中,每次选中一个新的临时标记结点,伴随着每次删除堆顶元素,可能有若干新的临时标记结点插入堆(具体跟图的连接结构有关),但堆中的节点个数从不会达到n个,堆高实际上可能小于甚至远小于O(logn),直至堆空,算法结束。因此O(logn)是堆高度上界的松弛描述,实际上可能远远低于这个量级,这造成了实际上的时间复杂度远低于理论上的时间复杂度。 综上,二叉堆优化的Dijkstra算法的时间复杂度实际上是: 而且这是一个非常松弛的上界,我们即使用实验得到他的时间复杂度为m的线性阶也不奇怪。不过接下来的这个巧妙的堆结构,能够从理论上把该算法的时间复杂度降为m的线性阶。 2.3 d堆优化算法 2.3.1 d堆优化算法的时间复杂度研究 首先我们对一般的d堆进行研究。我们改写程序得到用d堆优化的Dijkstra算法程序,然后设置d值为一般值——d取遍从5到15的所有值,再用前述同样的图数据输入d堆优化算法,用同样的方法处理实验结果。我们先以mlogdn和ndlogdn为最高次项,构建了可能包括nlogdn、dlogdn、logdn、m、n和常数项中的一项或若干项共26=64种所有形态的多项式模型,并进行最小二乘法拟合,将拟合结果汇成表格(同上,数据略),得到了同二叉堆类似的现象——最高次项mlogdn前的系数不统一,不稳定;而m项前的系数最为稳定,而且是否包含m项与模型的精准程度有着很大的相关性。我们综合误差与模型的复杂程度,选择出了两组相对比较好的模型(见表2的1、2号模型)。 同样我们去除最高次项mlogdn再一次拟合,考察了64种多项式模型,观察拟合结果,发现与前一次实验类似,拟合模型只要含有m项和nlogdn项,就能得到很好的拟合结果。这说明,mlogdn这一项对拟合精度影响很小。我们择优挑选出了3组拟合结果(见表2的3、4、5号模型)。 表2 d堆优化算法模型比较Tab.2 Binary Heap Optimization Algorithm Model Comparison Table 接下来我们尝试将ndlogdn这一项也去除,继续考察了64种多项式模型,作为对比试验,发现这次的拟合结果误差均不如人意,最好的模型其误差也超出其他组实验误差几倍之多。我们能够得出结论:ndlogdn是不可或缺的一项。 表2列出了以上每次选择所得到的较优的模型及其参数。 综合经验误差、推广误差、模型的复杂程度等多方面因素,我们选择5号模型。 作为最终的拟合结果。取其最高阶,可以认为:算法的复杂度被优化为Θ(m+ndlogdn)。 选择d=10时,其三维图像如图3所示: 图3 d堆优化算法函数图像(d=10)Fig.3 D-heap Optimization Algorithm Function Image(d=10) 这就证明,d堆优化的Dijkstra算法的时间复杂度已经达到了()O m。 2.3.2 d堆优化算法中关于d值的研究 在单纯的堆排序算法中,我们把d堆与二叉堆相比,不难证明,当d为e附近(即d=3)时,堆排序的时间性能可达到最优。在利用d堆作为存储结构的Dijkstra算法中,具体情况与单纯的堆排序算法有所不同,但我们容易知道,它也存在一个最优的d值,使该算法的时间复杂度达到最低。 在理论的证明中,我们令d=2+/m n,能够证明d堆优化算法的时间复杂度能够达到线性阶[11],但它并不是最优的d值。现在,我们想研究d为何值时,该算法方能达到最佳的优化效果。 我们令d从2取到40,对原数据进行大量的实验。限于篇幅,图4展示了部分结果。 图4 S-d关系图Fig.4 S-d relation Image 从图中可看出,每一条曲线都有一个最低值。在d从2开始增大时,操作总数S先是迅速降低,然后缓缓降低至最低值;然后又缓缓回升,并随着d的增大呈现稳定增长的趋势。曲线在最低值两侧的附近波动较小,形成一个小区间,我们可以认为最优的d值落在一个区间里。在这个区间的两侧,曲线都表现出明显的单调性。 从理论的角度来分析,开始操作总数S随着d值的增大而迅速降低,其原因是d堆的存储结构有效得降低了堆的高度,因为堆的高度logdn随着d的增大而减小。而当d值达到最优值之后,操作总数S随着d值的增大而增大,是因为在执行下渗操作时,节点要同时与d个儿子相比较,其时间复杂度为O( dlogdn),当d达到某个值的时候,下渗算法的时间复杂度会随着d的增大而增大,这也导致了整个算法时间复杂度的增大。 就我们所展示的这4种配置的图而言,它们的最优d值分别为6、6、7、5,而它们2+m/ n的值分别为14、42、47、42,这结果显示,使算法时间成本最低的d值与m、n并无关联,而是在一个比较稳定的范围内小幅波动——即d∈[5,7]。 如果我们把传统算法、二叉堆优化算法、d堆优化算法的结果画在同一张图中(图略),就能够明显得看出,以二叉堆作为存储结构,能够极大地优化Dijkstra算法,假如用d堆作为存储结构,选择合适的d值,该算法还能被进一步优化。 本文设计了一系列实验,研究了最短路径算法及其堆优化算法,得到如下结论: 1. 验证了Dijkstra传统算法的时间复杂度是Θ(n2)阶的。 2. 二叉堆优化的Dijkstra算法的时间复杂度可从理论上证明出是O( mlogn)阶,但实验可证明,对于稠密图,算法的时间复杂度可以用m和nlogn的线性函数表示。 3. 采用d堆优化,时间复杂度可降低为m、ndlogdn、nlogdn、dlogdn和n的线性函数。 4. d堆优化算法的参数d对复杂度有显著影响,变化趋势呈现某些共同特征,最优d值位于[5,7]区间。 该问题的实验研究可能会为另一个贪心算法--最小生成树的Prim算法的研究[13-15]带来一些新的启示。另外,理论会给我们提供正确的标尺和方向,而实验会带领我们踏上真理的大陆。所以,不满足于理论,勤于用实验去检验,才能不断地有新的发现。 [1] DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerical Mathematics, 1959, 1(1): 269-271. [2] Wang Shu-Xi, The Improved Dijkstra's Shortest Path Algorithm and Its Application[C]. Procedia Engineering, 2012, 29: 1186–1190. [3] Jayadev Misra. A walk over the shortest path: Dijkstra’s Algorithm viewed as fi xed-point computation[J]. Information Processing Letters, 2001, 77(2): 197–200. [4] Domenico Cantone, Simone Faro.Two-Levels-Greedy: a generalization of Dijkstra’s shortest path algorithm[J]. Electronic Notes in Discrete Mathematics, 2004, 17(10): 81–86. [5] 贺凯, 李韶杰, 吉亚威, 等. 移动机器人新型半智能路径导航系统的设计与实现[J]. 软件, 2013, 34(4): 1-6. [6] 徐彬, 王权锋, 刘斌, 等. 贪婪和A-Star算法在物流配送中的应用及仿真[J]. 软件, 2013, 34(6): 35-39. [7] 乐阳, 龚健雅. Dijkstra 最短路径算法的一种高效率实现[J]. 武汉测绘科技大学学报, 1999, 24(3): 209-212. [8] 严寒冰, 刘迎春. 基于GIS的城市道路网最短路径算法探讨[J]. 计算机学报, 2000, 23(2): 210-215. [9] 宋青, 汪小帆. 最短路径算法加速技术研究综述[J].电子科技大学学报, 2012, 41(2): 176-184. [10] T.H. Corman等, 算法导论(第三版)[M]. 潘金贵等译, 北京:机械工业出版社, 2013. [11] M.H. Alsuwaiyel, 算法设计技巧与分析[M]. 吴伟昶等译,北京: 电子工业出版社, 2010. [12] E. Horowitz, 数据结构基础(C语言版, 第二版)[M]. 北京:清华大学出版社, 2009. [13] 严蔚敏, 吴伟民. 数据结构(C语言版)[M]. 北京: 清华大学出版社, 2002. [14] C.F. Bazlamac, Khalil S. Hindi, Minimum-weight spanning tree algorithms: A survey and empirical study[J], Computers & Operations Research, 2001, 28(8): 767-785. [15] 李光杰, 王聪. 基于偏序堆的Prim 算法设计与实现[J]. 软件, 2014, 35(2): 67-69. Experimental Study of Heap Optimization of Dijkstra Shortest Path Algorithm ZHANG Han-lin1, GUAN Ai-wei1, FU Ke1, SUN Ting-kai2 Dijkstra shortest path algorithm is a classical algorithm of graph theory.Given graph G with n vertices and m arcs, the time complexity of this algorithm is Θ(m+n2).The predecessors' theoretical research shows that if the binary heap or d-heap is used as the auxiliary data structure, the time complexity of the algorithm can be reduced to varying degrees.However, what these previous studies have given is relatively relaxed upper bounds.In this paper, we design a series of experiments, using binary heap and d-heap to realize the optimization of the algorithm, and through the method of model fitting and regression to study the time complexity of the optimized algorithms.We find that for the dense graph, using the binary heap, the actual time complexity can be reduced to the linear function of m and nlogn; and using the d-heap, the time complexity can be reduced to the linear function of m, ndlogdn, nlogdn, dlogdnand n. Moreover, the value of d has a significant impact on the complexity in terms of some common varying characteristics, and the optimal value of d is located at [5,7]. Dijkstra shortest path algorithm; Binary heap; D-heap; Time complexity TP301.5 A 10.3969/j.issn.1003-6970.2017.05.004 南京理工大学江苏省级大学生科研创新训练项目“Dijkstra最短路径算法的堆优化研究” 张翰林,男,1995--,本科生,主要研究方向:信息与计算科学;关爱薇,女,1995--,本科生,主要研究方向:信息与计算科学;傅珂,女,1995--,本科生,主要研究方向:信息与计算科学;孙廷凯(本文通讯作者),男,1975--,副教授,主要研究方向。 本文著录格式:张翰林,关爱薇,傅珂,等. Dijkstra最短路径算法的堆优化实验研究[J]. 软件,2017,38(5):15-21
2 拟合实验
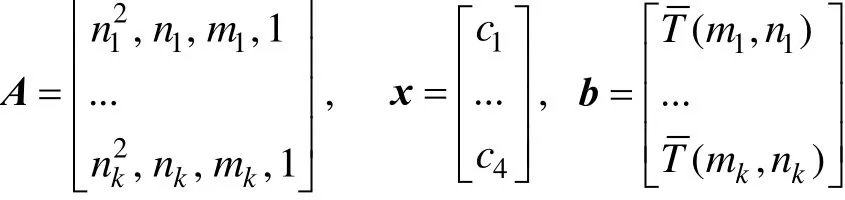
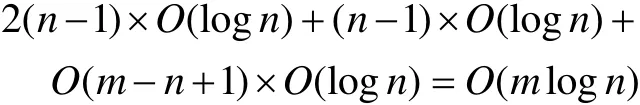
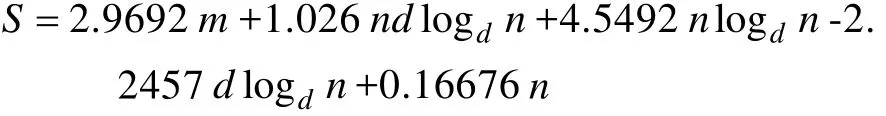

3 小结
(1. Nanjing University of Science and Technology, School of Science NJUST, Nanjing Jiangsu 210094; 2. Nanjing University of Science and Technology, School of Computer Science and Engineering, Nanjing Jiangsu 210094)

