数的整除

文︳张新春

数的整除

文︳张新春

数论是一门研究整数性质的学问，包括初等数论、解析数论、代数数论、丢番图逼近论、超越数论等分支。初等数论以算术方法为主要研究手段。为了与数的四则运算这种算术进行区分，也有人把初等数论称为高等算术。初等数论的最基本内容一直是小学数学的基础内容之一。由于其概念多，概念之间的联系紧密，并且很多时候都需要学生借助概念进行思维，对于以形象思维为主的学生来说，这部分内容是难点。但正因为初等数论的这些特点，也使得它成为培养学生思维能力的绝好材料。

初等数论的研究对象主要是整数。整数指的是…，-5，-4，-3，-2，-1，0，1，2，3，4，5，…。非负整数0，1，2，3，4，5，…称为自然数，而非0自然数就称为正整数。

整除有两种定义方式，一种是用除法定义：如果整数a除以整数b（b≠0），商是整数，且没有余数，我们就说a能被b整除，或者说b能整除a。还有一种是用乘法定义：称一个整数a能被另一个整数b（b≠0）整除，如果存在第三个整数c，使得a=bc。

目前的教材在编写时应用了用乘法定义的“整除”的内容而去掉了“整除”的名称。比如：通过举例2×6=12，我们把2和6都叫做12的因数，12则是6的倍数，也是2的倍数。这里就用了整除的乘法定义。

就我们习惯用除法定义整除的形式而言，若从较严格的角度考察，也还存在一些问题。比如最直接的是：任意两个整数相除（当然除数不为0），都会存在一个商和一个余数（有时候为0）吗？对确定的两个整数而言，商和余数都是唯一的吗？理由是什么呢？下面，我们就从较严格的角度考察数的整除。

如果把整数放到数轴上，那将是一些离散的点。

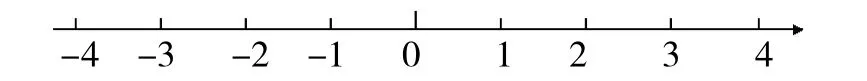
任何两个整数进行加、减或乘，其结果仍是整数。这个显然的特性，在数学上有一个专业的表述，叫做“整数集合对于加、减和乘法封闭”。但对于除法，情况就复杂一些。比如，两个整数a，b的商b≠0），这时，商当然是有理数，但未必是整数（尽管有可能）。但如果把这个商放在数轴上，要么和某个整数重合，要么介于两个相邻的整数之间。两种情况必居其一。不管出现哪种情况，以下表述所对应的整数总是存在的，并且是唯一的：

我们用一个专门的符号表示这个整数，就是[α]，这里的α可以是任意数。比如[2]=2，[-3]=-3，[π]=3，[-π]=-4。观察以下图示：

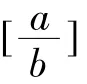
在小学数学中，我们习惯把a=bq+r记作以下的形式（当然，通常是在r不为0的情况下才这样记）：a÷b=q……r。

有这种意义上的不完全商和最小正剩余的除法，就叫作带余除法。这也说明，我们通常所谓的余数，是在整数除以整数，商也是整数的意义上说的，即一般不会说商是2.4，或余数是0.6之类。

我们之所以只考虑除数b＞0的情况，是因为如果除数b＜0的话，我们可以考虑，此时就转化为除数大于0的情况了。

简单地说，就是任意两个整数相除（除数大于0），其商要么是整数，要么就可以找到一个比这个商小，但最接近这个商的整数。后一种情况下的商是不完全商，被除数减去除数与不完全商的积，得到的数是最小正剩余，即通常所说的余数，余数要比除数小。而前一种情况，就是我们所说的整除。即对于整数a和整数b（b≠0）来说，如果存在第三个整数c，使得a=bc，则称整数a能被整数b（b≠0）整除。

如果一个整数a能被另一个整数b（b≠0）整除，我们记为b|a。显然，对于任意的整数a，都有1|a。而对任意的b（b≠0），有b|0。对任意a≠0，有a|a。但通常不说0|0。尽管的确存在整数c，使得0=0·c。

事实上，对任意的c，上述等式都成立，也许正由于不唯一性，使得我们通常不认为0|0。不过也有例外的说法，U·杜德利在教材《基础数论》中有一个练习题：“哪些整数整除零？”教材提供的答案是“所有整数”。（[美]U·杜德利.基础数论[M].上海科学技术出版社，1980）所有整数当然包括0。U·杜德利在定义整除时并没有规定b≠0，这至少说明，承认0|0也不会出现逻辑上的问题。从而我们可以这样认为，即讨论0|0是否成立并不是一个本质的问题。这个问题的答案取决于你如何定义整除。具体地说，就是你在定义整除时是否规定b≠0。不管规定b≠0还是不作这样的规定，都能自圆其说，都不会对数学产生什么实质性的影响。这也提醒我们，和小学生讨论“0是不是整除0”这样的问题是不恰当的，在小学生的作业或测试卷中出现这样的问题也是没有必要的、是不恰当的。若学生问到这类问题，可能的话，尽量把问题的相关背景告诉学生，不仅能保护学生的学习积极性，更重要的是让学生逐步形成科学的数学观。即逐步认识到数学“主要的应被看成人类的一种创造性活动，也即是一个包含有猜测、错误与尝试、证明与反驳、检验与改进的复杂过程”。（郑毓信.数学教育哲学的理论与实践[M].广西教育出版社，2008）

在本章接下来的讨论中，我们约定，若称整数a能被整数b整除，就表明b≠0。

关于整除，以下的结论是显然的。

若b≠0，c≠0，则

（1）若b|a，c|b，则c|a；

（2）若b|a，则bc|ac；

（3）若c|d，c|e，则对任意的m，n，有c|dm+en。

我们只证明（3）。

因为c|d，由整除的定义，存在整数g，使得d= cg。

同理，存在整数h，使得e=ch。

于是，对任意的m，n，dm+en=cgm+chn=c（gm+ hn）。即对于整数dm+en和整数c≠0，存在整数（gm+hn），使得dm+en=c（gm+hn）。

由整除的意义，上式就意味着c|dm+en。