基于多维模态方法的流体二维非线性强迫晃动分析
李遇春, 刘 哲, 王立时
(同济大学 水利工程系,上海 200092)
基于多维模态方法的流体二维非线性强迫晃动分析
李遇春, 刘 哲, 王立时
(同济大学 水利工程系,上海 200092)
基于多模态方法分析了二维容器内液体的强迫非线性晃动问题,采用绝对速度势函数描述动坐标下的流体非线性运动,根据Bateman-Luke变分原理,将非线性自由边值问题转化为等效的泛函极值问题,将自由液面波高函数和绝对速度势函数展开为广义 Fourier 级数,得到相互耦合的有限维非线性模态系统(一组非线性常微分方程),采用Runge-Kutta (龙格-库塔)法求解非线性常微分方程组,从而得到液体的强迫非线性晃动响应,分别模拟并讨论了矩形容器内液体在强地震作用下的晃动响应、在水平谐波作用下的普通共振稳态响应、在竖向谐波作用下的参数共振稳态响应,预测了液体在普通共振与参数共振共同作用下的液面响应。将多模态结果与其它数值方法的结果进行了对比, 计算结果表明,多模态方法在长时间非线性稳态响应分析上具有其独特的优势。
多维模态;二维非线性晃动;强震响应;共振响应;参数共振响应
在土木与水利工程结构设计中常常会遇到液体的强迫晃动计算问题,例如:贮液罐、渡槽、水库、反应堆冷却水柜等结构物在地震作用或其它周期性荷载(例如波浪等)下,液体的强迫晃动计算是贮液结构设计中必须涉及的问题,一般需要计算液体自由表面上的波高反应以及作用在容器壁上的液动压力等。
Ibrahim[1]详细综述了液体强迫晃动的研究历史与现状,现有许多研究是基于小幅晃动假设进行的,所得到的液体运动方程及边界条件为线性方程,然而当外部激励较大时,或液体的晃动幅度较大时,液体运动的非线性项不可忽略,大幅晃动时,非线性的因素支配了流体动力学特性,这些特性用线性理论无法解释,因此需要了解液体的强迫非线性晃动问题,由于液体晃动控制方程是非线性的,且自由液面位置事先是未知的,因而这个问题的研究和求解是相当困难的,尽管现有许多数值方法[2], 例如:边界元法[3-4]、有限元法[5]、SPH(Smoothed Particle Hydrodynamics)方法[6]等都能模拟流体的非线性晃动问题,但许多数值方法都难以模拟长时间的大幅晃动行为,难以从理论上去揭示晃动的非线性特征。解析(或半解析)方法仍然是液体晃动问题研究的一个重要方法,一般采用流体势流理论来分析液体的晃动,但通常都局限于小幅线性晃动问题[7-8],Faltinsen等[9]于2000年提出了液体有限幅晃动的多维模态解析方法,并用这个方法研究矩形容器内液体的非线性晃动特征,余延生等[10]采用多维模态方法分析了圆柱形贮液容器内液体的非线性晃动问题。对于矩形容器内的二维晃动问题,Faltinsen等最后推导结果的部分计算系数有误,且并未讨论在地震激励、参数激励等作用下的非线性强迫晃动问题。
本文基于Faltinsen等的研究,详细给出二维非线性晃动的多维模态方法的推导过程,采用多维模态方法模拟了矩形容器内液体在强地震作用下的晃动响应、模拟了在谐波作用下的共振稳态响应,模拟了液体的参数晃动,并预测液体在普通共振与参数共振共同作用下的液面响应。
1 二维非线性强迫晃动运动方程
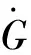
2Φ=0 (x,z)∈Ω(t)
(1)
(2)
(3)
(4)
式中:g为重力加速度;n为液体区域Ω(t)表面的外法线向量,其中
(5)
式中,i,k为单位基矢量。上述自由表面边值问题中:式(1)为液体连续性方程,式(2)为固壁边界条件,式(3)为自由液面运动学边界条件,式(4)为自由液面动力学边界条件。上述方程组的待求未知量为绝对速度势函数Φ(x,z,t)及波高函数h(x,t)。

图1 二维容器中液体的非线性晃动Fig.1 Nonlinear sloshing of fluid in a 2D tank
由Bernoulli方程,液体区域Ω(t)内的液体压力p可由式(6)确定
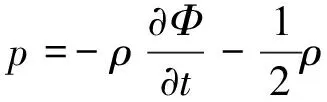
(6)
式中,ρ为液体的质量密度。于是作用在二维容器(单位厚度)上的力F(t)与力矩M(t)分别为
(7)
式中,r=xi+zk为液体粒子在坐标下的径向矢量。
2 基于压力积分的Bateman-Luke变分原理
利用Bateman-Luke变分原理[11-12],描述液体晃动的非线性自由表面边值问题式(1)~式(4)可由下列函数极值的必要条件得到
(8)
式中,L即Lagrange函数,L为下列压力积分
L=∫∫Ω(t)pdxdz=-ρ∫∫Ω(t)×
(9)
注意到泛函J为绝对速度势函数Φ(x,z,t)及波高函数h(x,t)的函数,泛函J取极值的必要条件为
δJ=δJ(Φ,h)=-ρδ×
(10)
其中函数Φ(x,z,t)及h(x,t)应满足式(11)
(11)
根据复合函数的变分规则,对式(10)进行变分运算有
(12)
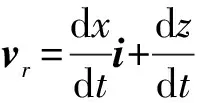
(13)
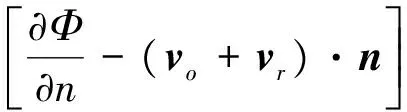
(14)
(15)
在湿边界上∂Sw(t)上,vr=0,所以式(14)等同于式(2);在自由边界上∂Sf(t)上,vr·n=ht(nz·n)=ht/|F|(其中:nz=(0,1)T,n=F/|F|,F=(-∂h/∂x,1)T),所以式(15)等同于式(3)。
由以上推导可以看出Bateman-Luke变分方程式(10)与液体晃动的控制方程与全部边界条件完全等价,变分方程式(10)表达了一个极其完美的变分原理,这样一个复杂非线性边值问题(式(1)~式(4))可转化为一个泛函J的极值问题,通过求解泛函J的极值问题从而得到原问题的解答。
3 基于变分原理的有限幅晃动非线性微分方程组(模态系统)
将绝对速度势函数按式(16)展开
Φ(x,z,t)=v0·r+φ(x,z,t)
(16)
式中:v0·r为牵连速度势;φ(x,z,t)为相对速度势,将式(16)代入式(1)~式(3)得
(17)
将自由液面波高函数h(x,t)和相对速度势函数φ(x,z,t)展开为下列的Fourier 级数
(18)
(19)
式中:βn(t)、Rn(t)(n=1,2,3,…)为广义坐标;hn(x)(n=1,2,3,…)为自由表面模态基函数,它与自由表面的振型函数一样,是一个完备的正交函数系;φn(x,z)(n=1,2,3,…)也为一个完备的函数系,由于这种完备性,可以保证上述的级数解能收敛到真实解答。实际应用时,φn(x,z)及hn(x)可取为(线性)液体系统的特征函数,这些特征函数可由线性模态分析得到。
将Φ的分解表达式(16)代入式(9)得
(20)
式中,
(21)
Lagrange函数的独立变量变为βn(t)及Rn(t)(n=1,2,3,…),将(20) 式代入(10)式,有
(22)
上面的推导中,系数l1,l2,An,Bnk均默认为βn(t) (n=1,2,3,…)的函数。由于δβi,δRn(t)可为任意值,要使式(22)成立,必须有
(23)

(24)
式(23)与式(24)为描述液体二维有限幅晃动的(无穷维)非线性微分方程组。式(23)将变量βn(t)及Rn(t)联系在一起,可通过渐近近似方法将Rn(t)表示为βn(t)的函数关系,将其代入式(24),便可得到关于βn(t)的二阶非线性常微分方程组,采用数值方法可求解这个非线性常微分方程组,得到βn(t)的时程解,进而可得到Rn(t)的时程解,最后再代入式(18)与式(19),得到问题的解答。
基于变分原理将一个连续系统的非线性边值问题转化为一个无穷自由度离散系统的动力学问题,这个离散系统也称之为(非线性)模态系统,相对于原始系统而言,求解这个非线性模态系统动力学问题要简单得多。
4 二维矩形容器内流体的非线性(有限幅)强迫晃动
4.1 有限幅晃动非线性微分方程组
考虑一个矩形容器(如图2所示),液体自由表面波高可由式(18)表示。根据线性模态分析的结果,对于矩形容器而言,式(18)与式(19)中的完备基函数可以取为
(25)
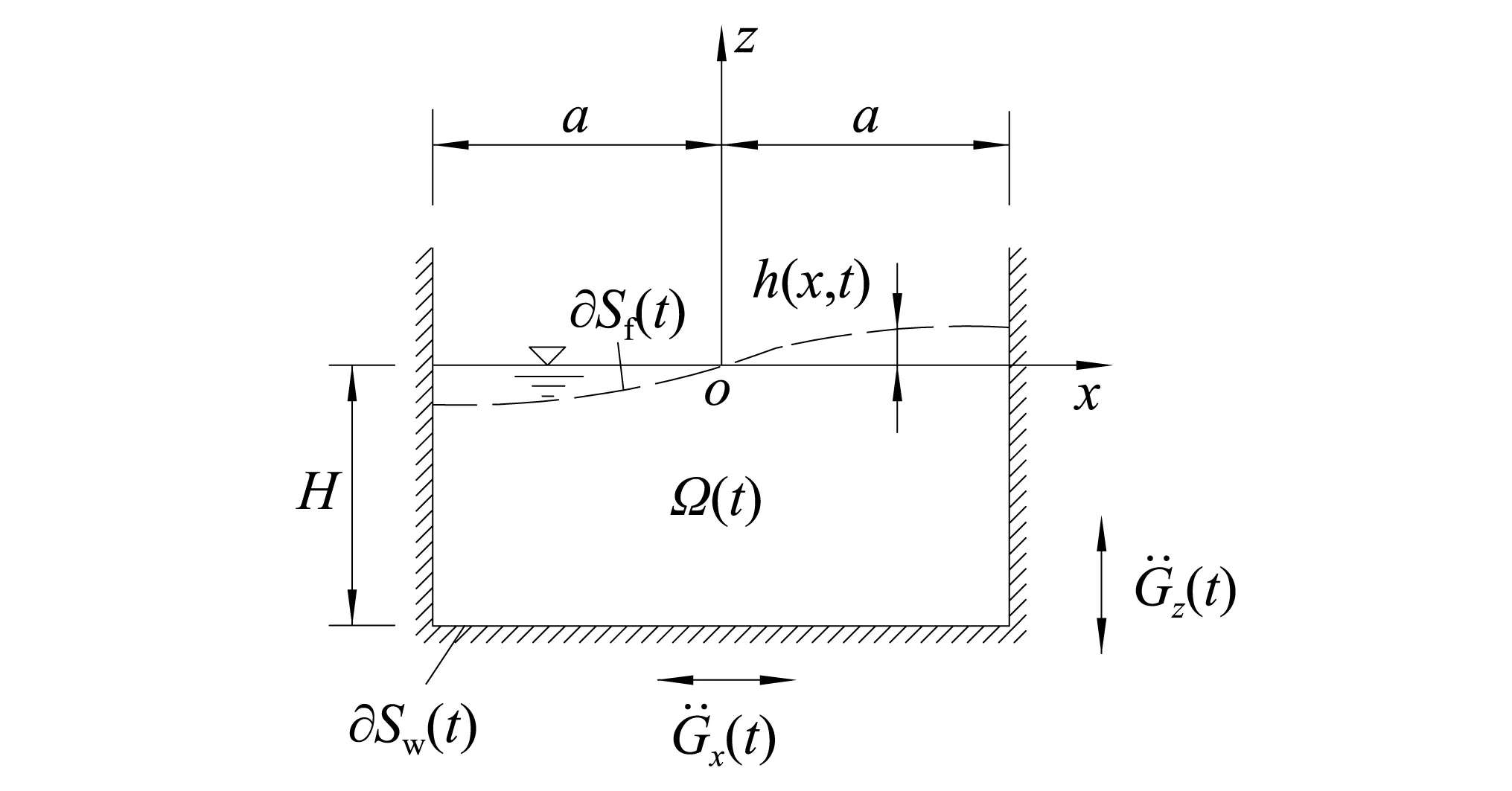
图2 矩形容器内液体的有限幅晃动Fig.2 Finite-amplitude sloshing of fluid in a rectangular tank
于是式(18)与式(19)具有下列形式
(26)
式(21)中的系数均与自由表面波高函数h(x,t)有关,仅取其表达式(26)的前三项(i=1,2,3),将式(21)中的系数都展为βi的幂级数,经逐项积分得
(27)
其中,
(28)
另外设
(29)
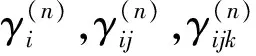
(30)
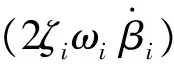
(31)
(32)
(33)
以上方程的系数按下式计算
(34)
(35)
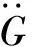
在进行动力(地震)响应的非线性晃动分析时,若仅考虑前三个(非线性)模态的影响,可采用非线性微分方程式(31)~式(33)进行数值求解,由于液体晃动第一阶模态具有主要贡献,因此取前三阶模态方程进行计算,通常可获得较好的计算精度。具体求解方程式(31)~式(33)时,首先需要将二阶常微分方程组化为标准的一阶常微分方程组,引入下列的变量替换
(36)
于是方程式(31)~式(33)变为下列的一阶微分方程组
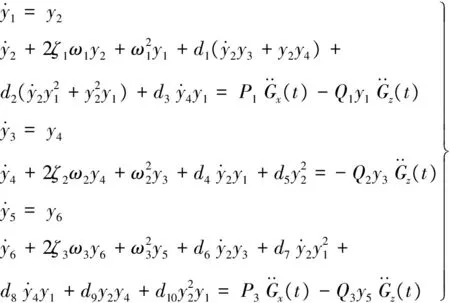
(37)
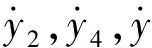
(38)
其中,
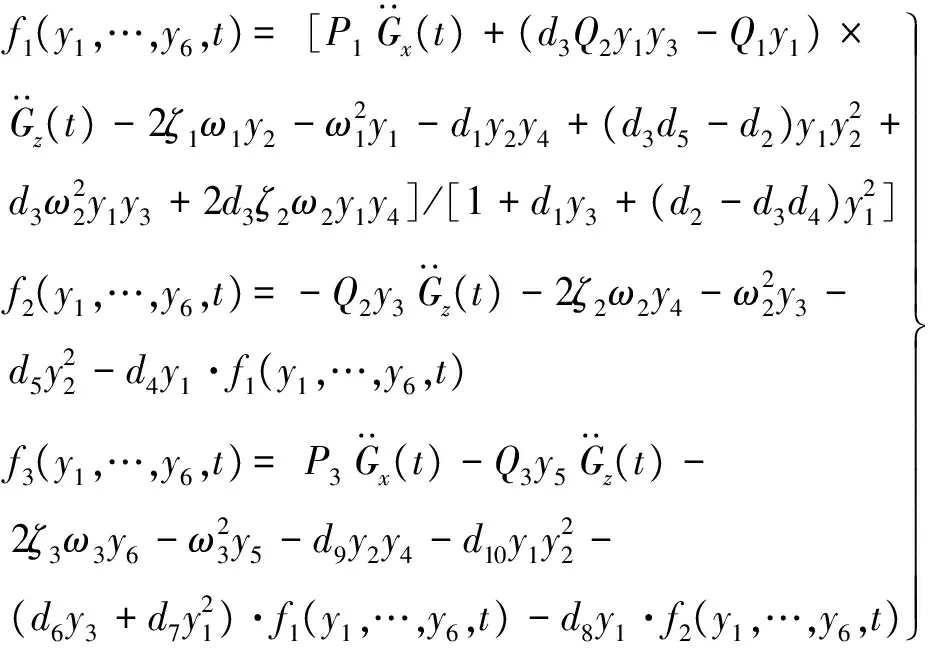
(39)
初始条件为
(40)
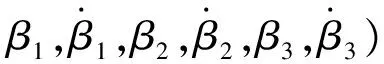
4.2 非线性强迫晃动算例
(1)水平地震作用下的非线性晃动响应
设矩形容器内静止水截面尺寸为2a=8.0 m,H=6.0 m,容器内流体的一阶自然晃动频率为ω1=1.94 rad/s,采用EL-Centro(N-S)地震波(峰值加速度为3.417 m/s2)作为水平地面加速度,采用非线性微分方程组式(38)进行数值求解,图3为无阻尼情形下(ζ1=ζ2=ζ3=0)波高h(a,t)地震响应曲线,同时采用边界元法及有限体积法(Fluent程序)进行相同的计算,计算结果见图3,从图中可以看出三个方法得到的结果比较吻合,多模态结果与有限体积法(Fluent程序)得到的结果吻合良好,表明多模态理论与公式正确。
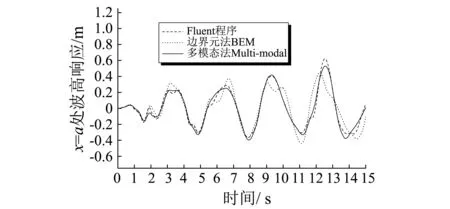
图3 EL-Centro(N-S)水平地震作用下的波高地震响应Fig.3 Wave-height response to EL-Centro (N-S) seismic excitation
(2)水平谐波激励下的非线性共振稳态响应
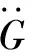
图5(a)为采用多模态方法得到的无阻尼情形下的
波高的共振反应曲线,由图可以看出,在共振初始阶段,流体的晃动幅度呈线性逐步增大,当达到最大值后,晃动幅度不再增大,振幅出现了时大时小的所谓“拍”现象,在某些实验中已观察到这一现象;图5(b)为有阻尼情形下(ζ1=ζ2=ζ3=0.01)的共振反应曲线,由图可以看出,晃动的“拍”现象消失,说明阻尼将晃动响应“抹平”了。
在线性晃动理论中,线性方程预测的共振幅值将无限增大,这是因为线性方程中未考虑非线性项的影响,当晃动幅值较大时,非线性项将起到越来越大的作用,非线性项抑制了晃动幅度的无限增大,从而出现了有限幅的稳态响应。某些数值方法(如边界元法、SPH方法等)很难模拟长时间的稳态大幅响应,而多模态方法在很长的时间内具有良好的数值计算稳定性,这正是多模态方法的突出优点。
图4 谐波作用下的共振响应(无阻尼)Fig.4 Resonance response to harmonic excitation (without damping)
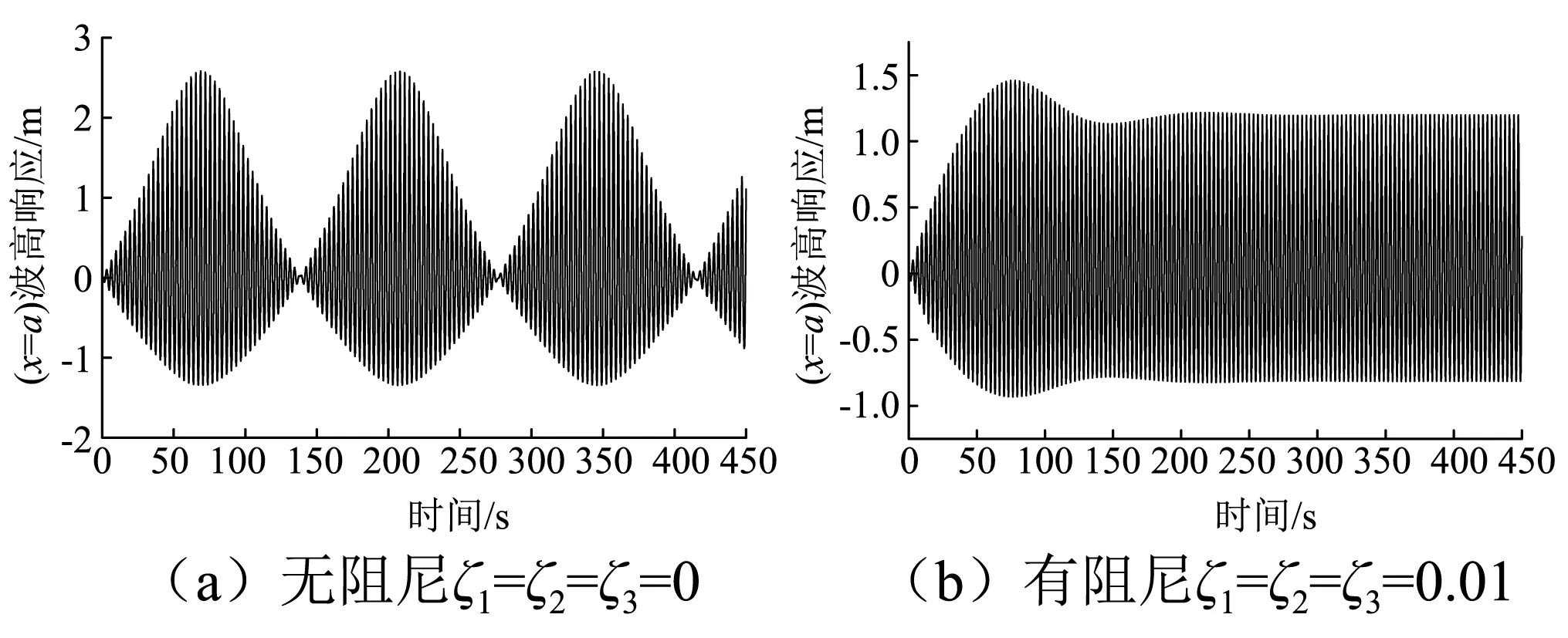
图5 多模态共振响应稳态解Fig.5 Steady-state solutions of resonant response by the multimodal method
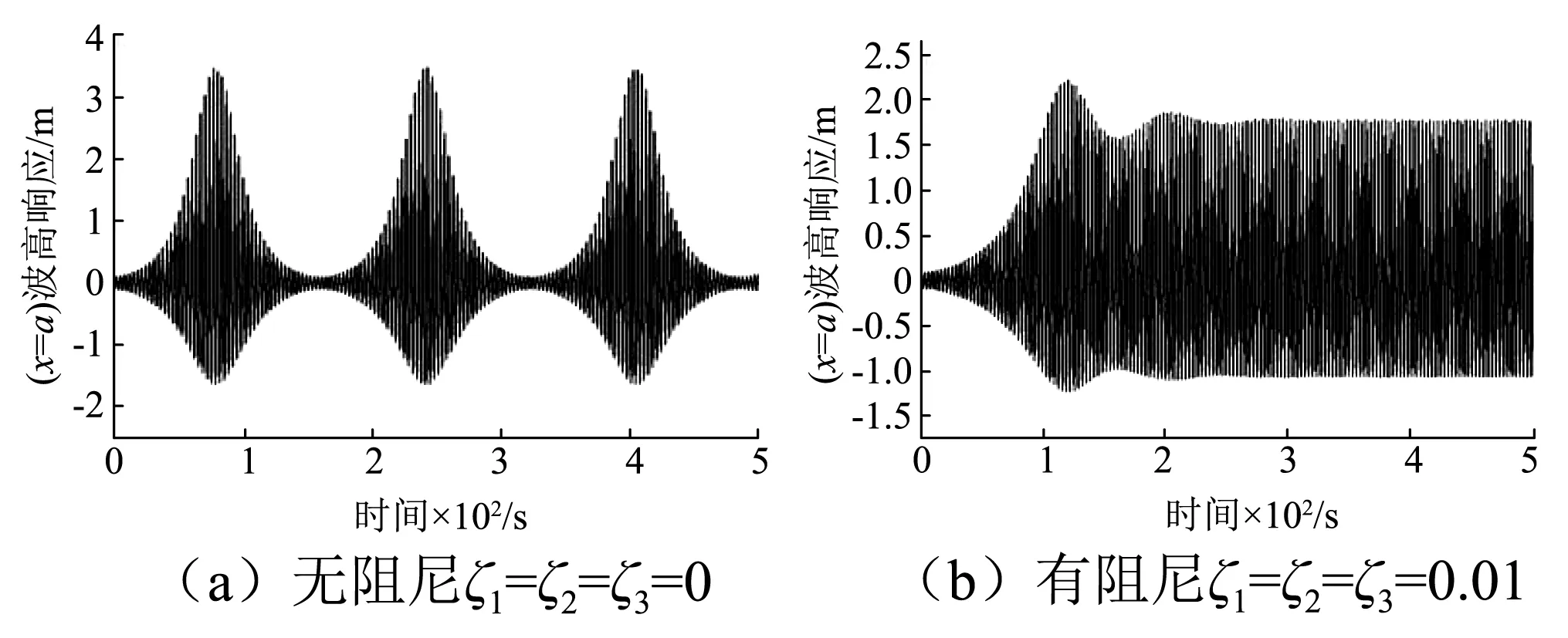
图6 参数共振响应稳态解Fig.6 Steady-state solutions of parametric resonant response by the multimodal method
(3)竖向谐波激励下的参数共振响应
(4)普通共振与参数共振同时发生的液体晃动响应

图7 普通共振与参数共振同时发生时的波高响应Fig.7 Wave-height response to the combination of the ordinary and parametric resonances
5 结 论
本文基于多模态方法分析了二维容器内液体的强迫非线性晃动问题,本文分别模拟了矩形容器内液体在强地震作用下的晃动响应,模拟了在水平谐波作用下的共振稳态响应,模拟了竖向谐波作用下的参数共振稳态响应,两种共振响应结果与实验现象相符;预测了液体在普通共振与参数共振共同作用下的液面响应。本文将多模态结果与其它数值方法的结果进行了对比分析, 结果表明: 在液体晃动幅度不大时,多模态结果与其它方法的结果吻合良好,但液面幅度较大时,多模态方法具有其独特的优势,特别适用于液体长时间的非线性稳态响应分析。
由于多模态法为解析方法,依赖于表面波函数的连续性,当外加激励幅值较大时,自由表面波可能破碎(不连续),这时多模态方法将不再适用。
[ 1 ] IBRAHIM R A. Liquid sloshing dynamics: theory and applications [M]. Cambridge: Cambridge University Press, 2005.
[ 2 ] IBRAHIM R A, PILIPCHUK V N, IKEDA T. Recent advances in liquid sloshing dynamics [J]. Applied Mechanics Reviews, 2001, 54(2):133-199.
[ 3 ] NAKAYAMA T, WASHIZU K. The boundary element methd applied to the analysis of two-dimensional nonlinear sloshing
problems [J]. International Journal for Numerical Methods in Engineering, 1981,17:1631-1646.
[ 4 ] 李遇春,楼梦麟. 渡槽中流体非线性晃动的边界元模拟[J].地震工程与工程振动,2000,20(2):51-56. LI Yuchun, LOU Menglin. BEM simulation of nonlinear sloshing for aqueduct fluid [J].Earthquake Engineering and Engineering Vibration,2000,20(2):51-56.
[ 5 ] RAMASWAMY B, KAWAHARA M. Arbitray Lagrangian-Eulerian finite element method for unsteady, convective, incompressible viscous free surface fluid flow [J]. International Journal for Numerical Methods in Fluids, 1987, 7(10):1053-1075.
[ 6 ] WANG L, WANG Z, LI Y. A SPH simulation on large-amplitude sloshing for fluids in a two-dimensional tank [J]. Earthquake Engineering and Engineering Vibration, 2013, 12(1):135-142.
[ 7 ] 房忠洁, 周叮, 王佳栋,等.带隔板的矩形截面渡槽内液体的晃动特性[J].振动与冲击,2016,35(3):169-175. FANG Zhongjie,ZHOU Ding,WANG Jiadong,et al.Sloshing characteristics of liquid in a rectangular aqueduct with baffle[J].Journal of Vibration and Shock,2016,35(3):169-175.
[ 8 ] LI Y, WANG J. A supplementary, exact solution of an equivalent mechanical model for a sloshing fluid in a rectangular tank[J]. Journal of Fluids and Structures, 2012,31(5):147-151.
[ 9 ] FALTINSEN O M, ROGNEBAKKE O, LUKOVSKY I A, et al. Multidimensional modal analysis of nonlinear slsohing in rectangular tank with finite water depth [J]. Journal of Fluid Mechanics, 2000,407:201-234.
[10] 余延生, 马兴瑞, 王本利. 利用多维模态理论分析圆柱贮箱液体非线性晃动[J].力学学报,2008,40(2): 261-266. YU Yansheng, MA Xingrui, WANG Benli. Analyzing liquid nonlinear sloshing in circular cylindrical tank by multidimensional modal theory [J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(2): 261-266.
[11] LUKE J C. A variational principle for a fluid with a free surface [J]. Journal of Fluid Mechanics,1967, 27:395-397.
[12] FALTINSEN O M,TIMOKHA A N. Sloshing [M]. Cambridge: Cambridge University Press, 2009.
[13] 徐士良. FORTRAN常用算法程序集 [M]. 北京:清华大学出版社, 1992.
[14] LI Y, WANG Z. Unstable characteristics of two-dimensional parametric sloshing in various shape tanks: theoretical and experimental analyses [J]. Journal of Vibration and Control, 2015, 6(2):349-359.
A multimodal-based analysis for two-dimensional fluid nonlinear forced sloshing
LI Yuchun, LIU Zhe, WANG Lishi
(Department of Hydraulic Engineering, Tongji University, Shanghai 200092, China)
The problem of fluid nonlinear forced sloshing in a two-dimensional tank was analyzed by using the multimodal method. The absolute velocity potential was introduced to describe the nonlinear motion of fluid in a moving frame. Based on the Bateman-Luke variational formulation, the nonlinear (free) boundary value problem was transformed into an equivalent functional extreme value problem. A finite-dimensional nonlinear coupled modal system (a set of nonlinear ordinary differential equations) was obtained by expanding the functions of free surface wave-height and the absolute velocity potential into the generalized Fourier series. By using the Runge-Kutta algorithm, the nonlinar ordinary differential equations could be solved, and the nonlinear forced sloshing responses were further acquired. The time-history response to strong seismic excitation, the stead-state common resonance response to the horizontal harmonic excitation, and the stead-state parametric resonance response to the vertical harmonic excitation were respectively simulated and discussed for the fluid in a rectangular tank. The combined resonance responses of the free surface to the horizontal and vertical harmonic excitations were further predicted. The solutions by the multimodal method were compared with those by other numerical formulations. The results show that the multimodal approach has its unique advantage in the long-time nonlinear analyses of stead-state responses.
multimodal; two-dimensional nonlinear sloshing; strong earthquake response; resonance response; parametric resonance response
国家自然科学基金资助项目(51279133)
2016-01-27 修改稿收到日期: 2016-06-16
李遇春 男,博士,教授,博士生导师,1962年2月生
TV 312; O 353.1
A
10.13465/j.cnki.jvs.2017.16.025

