基于功率流有限元方法的异形薄板能量密度求解
刘知辉, 牛军川,2, 周一群
(1.山东大学 机械工程学院,济南 250061;2. 山东大学 高效洁净机械制造教育部重点实验室,济南 250061)
基于功率流有限元方法的异形薄板能量密度求解
刘知辉1, 牛军川1,2, 周一群1
(1.山东大学 机械工程学院,济南 250061;2. 山东大学 高效洁净机械制造教育部重点实验室,济南 250061)
在机械工程中,对结构在不同频率激励下的振动响应进行分析预测具有重要的意义。功率流有限元法以其适用频率范围较广,可得到结构响应的细节信息等优点成为振动分析领域的研究热点。利用功率流有限元方法对薄板的弯曲波能量密度进行了求解,使用加权残差法导出了薄板单元节点的能量密度残差,利用线性四边形网格对薄板进行网格划分并在此基础上建立了单元的有限元方程,进一步地通过对单元有限元方程的组装和求解得到了薄板上各个节点处的能量密度响应,引入线性三角形网格以处理复杂形状薄板能量密度的求解,对使用功率流有限元方法求解任意形状薄板上的能量密度分布问题具有一定意义。
振动;功率流有限元分析;异形薄板;能量密度
结构的振动对结构的性能、寿命有重要影响,对于给定的结构,在设计阶段使用有效的分析方法对结构的振动响应进行分析并得到较为准确的结果对于结构的设计和应用具有重要的意义[1]。
传统的结构振动分析方法主要有基于位移的有限元方法和基于能量的统计能量法,其中有限元方法在低频时可以较为准确地预测结构的振动响应,但当频率增大时,为了准确得到结构的响应不得不对网格进行细化,由此带来的不断增加的运算量最终将使得计算变得不可行,且在高频时结构的响应对结构的细节变得极为敏感,表现出混沌的现象,有限元建模过程中对细节的忽略以及数据的不确定性使得在高频时分析得到的结果不具有可信性,因此,在高频时使用有限元方法难以有效的预测结构的响应[2]。统计能量法在分析结构的高频振动时具有较大的优势,可以较为准确的预测高频时结构在统计意义下的响应。然而由于统计能量法在求解结构的动态响应时一般将具体的耦合结构划分为若干个子系统,最终求解得到每个子系统在统计意义下的平均能量响应,无法再提供子系统内部细节信息,因此当需要了解子系统内局部的响应时,统计能量法便不再适用[3]。由Nefske等[4]提出的功率流有限元方法将结构中每一微元视为一子系统,利用能量平衡关系建立结构的能量密度控制方程,并进一步的通过求解能量密度控制方程得到结构的能量密度响应。与传统的有限元方法相比,该方法可较为有效的分析结构的中高频振动响应,与统计能量法相比,该方法可得到结构内局部响应的信息,因此该方法在结构中高频动力学分析领域具有较大的优越性。在Nefske等完成了功率流有限元开创性的工作后,众多学者对具体结构的能量密度控制方程和耦合结构间的能量传递关系进行了研究[5-7]。
板是在工程实际中常见的结构,在许多耦合系统中板的辐射声是系统向外辐射声能的重要组成部分,因此使用功率流有限元方法研究外界激励下板的能量密度分布具有重要意义。Bouthier等[8-9]先后研究并建立了薄膜和薄板的弯曲波能量密度控制方程,Park等[10]对薄板的面内波能量密度控制方程进行了研究并基于此研究了两块矩形板耦合时能量传递特性,李坤朋[11]研究了矩形薄板以及矩形薄板中存在加强筋时板上能量的分布和传递,Niu等[12- 13]研究了考虑三种波形情况下耦合板的能量密度求解,江民圣等[14]研究了两矩形薄板以任意角度耦合时板中能量密度的分布与传递特性。上述研究对功率流有限元方法应用于结构中板的能量密度求解有着重要意义,但这些研究都以规则的矩形板为研究对象,且划分的单元皆为统一的矩形单元,对于工程实际中应用更为广泛的形状不规则薄板无法进行仿真计算,且缺少相关研究。
本文利用功率流有限元方法对薄板的能量密度进行了求解,利用加权残值法建立了单元节点的能量密度残差方程,使用线性四边形单元对形状较规则薄板进行网格划分,求解了薄板的能量密度分布并对薄板中的能量密度分布和能流进行了可视化,进一步的利用三角形单元对复杂形状的薄板进行网格划分并建立了三角形单元的能量密度有限元方程,同时对不同单元类型混合使用时的单元兼容性进行了讨论,三角形单元的引入以及不同单元类型的混合使用可以有效的将功率流有限元方法应用范围扩展至任意几何形状的薄板结构。
1 能量密度控制方程
如图1所示,薄板受到外界的激励后产生对应的响应,从而获得动能与势能,定义能量密度为单位面积内动能与势能的总和,也即
e=T+V
(1)
式中,e、T和V分别为系统的总能量密度、动能和势能。若薄板处于稳态,则其任意位置处能量密度为常数,即
(2)
如图2所示,考虑处于稳态的薄板内任意一微元内的能量平衡关系
-∫Γn·qdΓ-pdiss+pin=0
(3)

图1 受功率激励的薄板Fig. 1 Thin plate excited by the power input
式中:q为能流强度;Г为微元的边界;n为微元单元边界外法线方向矢量;pdiss为结构阻尼引起的能量耗散;pin为外界的功率输入。式(3)刻画了微元内的能量平衡关系。

图2 微元内的能量平衡Fig. 2 Energy balance in the infinitesimal element
基于平面波远场叠加原则和式(3),Bouthier等分别具体的导出了各向同性有限薄板的弯曲波和面内波的能量密度控制方程
(4)
式中:cg为弹性波的群速度;η为结构损耗因子;ω为激励圆频率;Δ(·)二维拉普拉斯算子;e为周期平均以及局部空间平均意义下远场波能量密度;πin外界输入功率。
式(4)确定了能量密度在薄板内的分布情况,其中群速度cg由弹性波的具体类型确定,当弹性波为具有非频散特性的面内弹性波时,群速度cg与波速c的关系为cg=c,当弹性波为具有频散特性的板面外弯曲波时cg= 2c。 Seo等[15]使用单傅里叶级数类型的Lévy解对式(4)进行求解,该方法对求解域有较高的要求,难以应用于复杂的求解域。Pereira等[16]使用谱元法对式(4)进行求解,同样存在不能适用于复杂求解域的缺陷。有限元可适用于复杂求解域,并可将结构的局部特性考虑在内,因此可考虑使用有限元方法对式(4)进行求解。由于能量密度e的泛函不易获得,因此难以通过变分原理建立式(4)有限元方程,可考虑使用以形函数作为权函数的加权残差法对式(4)进行求解。
单板结构一般主要考虑其弯曲波的影响,式(4)对于薄板内的弯曲波能量密度控制方程的研究基于薄板的Kirchhoff-Love理论,此时薄板的变形使用中性层的挠度进行描述,且式(4)在建立过程中已对厚度方向进行积分,因此对薄板上能量密度的求解类似于平面应力问题的求解,能量密度仅取决于板的面内位置而与厚度方向位置无关,因此在使用有限元方法对板上的能量密度进行求解时,应使用二维平面网格对薄板的几何区域进行离散。在形函数加权下,离散后所得到的二维平面网格单元Ω的节点所对应的残值为
(5)
式中,R(e)为单元节点残差,其他各参数意义与式(4)相同,利用形函数N对单元内的场变量e进行插值
e=N·en
(6)
式中,en为单元节点处的能量密度,利用微分运算法则对式(5)等号右侧第一项进行变换
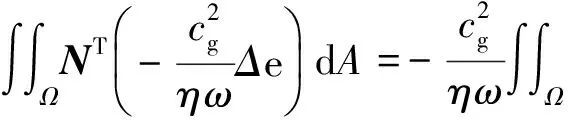

(7)
由散度定理,式(7)等号右侧第一项可表为
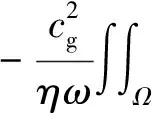
(8)
从而式(5)可表为
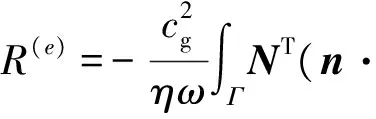
∫∫ΩηωNTNdA·en-∫∫ΩNTπin(x,y)dA
(9)
令应变矩阵为
BT=
(10)
则表征薄板单元能量传递效应的单元矩阵为
(11)
表征薄板单元能量耗散效应的单元矩阵为
(12)
令
(13)
与外界能量输入有关的单元输入功率向量为
F(e)=∫∫ΩNTπin(x,y)dA
(14)
与单元边界能量密度梯度有关的向量为
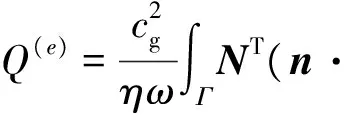
(15)
从而薄板单元的节点残差可表为
R(e)=K(e)en-Q(e)-F(e)
(16)
在计算得到各单元的有限元方程后,可按照各单元对节点残值的贡献关系将各单元所对应的式(16)进行组装,其过程与静力学有限元求解的有限元方程组装相似,在组装时由于能量密度为不具有方向性的一维场变量,且在计算单元矩阵时取各个单元的局部坐标系坐标轴相互平行,因此不需再进行坐标变换。与单元边界能量密度梯度有关的向量Q(e)反映了经由单元边界传导的功率流,容易看出,在进行单元组装,建立薄板的整体有限元方程式的过程中,位于薄板内部单元的Q(e)将相互抵消而不对薄板的能量密度分布产生影响,组装得到的整体有限元方程为
R=Ke-Q-F
(17)
式中:K为对各单元矩阵进行组装后得到的整体矩阵;F为外界对薄板的功率输入向量;e为节点能量密度向量;若薄板的边界无能量流出,则边界处的Q(e)亦为0。为使得所建立的整体有限元方程尽可能满足薄板能量密度控制方程,各节点残值应为0,从而薄板的整体有限元方程为
Ke=F
(18)
2 任意形状板的能量密度求解
2.1 线性四边形单元
功率流有限元方法视能量密度基本未知量,不再关注于结构振动的模态与波长,因此网格划分的密度不再受激励频率的影响,当输入的频率增大时不需再划分过于细密的网格。薄板能量密度为无方向性的一维场变量,在使用四节点的线性四边形单元时,其单元形函数的形式为
N=[N1N2N3N4]
(19)
如图3所示,可将划分得到的物理坐标下的四边形单元映射为自然坐标下的等参单元。

图3 薄板等参单元的转换Fig. 3 Thin plate’s isoparametric element transition
在自然坐标下线性四边形单元的形函数可表为自然坐标(ξ,ζ)的函数,若第m个(m=1, 2, 3, 4)节点的自然坐标为(ξm,ζm),则该点所对应的形函数为
(20)
物理坐标系与自然坐标系下面积微元之间的关系为

(21)
J为坐标映射雅可比矩阵
J=[∂ξN∂ζN]TX
(22)
式中,X为线性四边形单元节点的物理坐标以行排列的形式组成的矩阵,则应变矩阵
(23)
在将四边形单元由物理坐标映射到自然坐标后,相应的单元矩阵可在自然坐标系下计算得到,其中表征单元能量传递特性的矩阵为
(24)
单元的能量耗散矩阵为
(25)
式(24)与式(25)中的积分均可借助于数值解法求解。当薄板为规则的矩形时,使用规则的矩形单元便可实现网格划分,此时式(24)与式(25)中的积分为多项式积分,借助高斯积分可计算得到精确的单元矩阵,通过单元矩阵的组装求解便可得到所划分的矩形单元节点处能量密度响应。四边形单元亦可应用于其他不规则求解域,但此时便难以再划分出矩形单元。当采用非矩形的四边形单元时,单元所对应的雅可比矩阵不再为常数阵,式(24)中的积分也不再为多项式积分,因此使用高斯积分不能得到式(24)精确值。但当所划分出的四边形单元与矩形单元较为接近时,可以认为雅可比矩阵在单元内的变化较小,在将其视为常数矩阵的情况下仍可使用高斯积分进行计算。
以一不规则四边形板为计算实例,该四边形板的左右两边长度分别为1 m,1.12 m,上下两边长度分别为1.5 m,1 m,由于几何形状较为规则,使用四边形单元对其进行网格划分。计算所使用参数如表1。

表1 薄板参数表
在该四边形板的形心位置处模拟外界激励施加集中单位功率激励,并使用δ函数表示该形式的激励
πinP·δ(x-x0)·δ(y-y0)
(26)
从而对于存在外界功率激励的单元,与外界能量输入有关的单元输入功率向量为
F(e)=∫∫ΩN(ξ0,ζ0)T·P·δ(ξ-ξ0)·δ(ζ-ζ0)dA=
P·[N(ξ0,ζ0)]T
(27)
在式(24)中,薄板的弯曲波群速度cg为
(28)
式中,D为薄板的弯曲刚度。
使用高斯积分别对式(24)和式(25)进行求解,在得到各个单元的有限元矩阵后通过组装与求解可得到节点处的能量密度响应,进一步的利用式(6)进行插值可得单元内部任意位置处的能量密度。为更直观的对比各位置处能量密度响应大小,可采用功率级表示能量密度的大小
LP=10·lg(P/P0)
(29)
式中,P0为基准能量密度,取P0=1×10-12J/m2。在平面波远场叠加假设下,经过周期平均以及局部空间平均后的能量密度e与功率流q之间关系为

(30)
也即功率流沿能量密度的负梯度方向,将式(6)代入式(30),可得
(31)
图4为薄板在单点激励下的能量密度响应以及功率流分布情况,由图4可知,能量密度响应在激励点处取得最大值,由于结构阻尼的效应,能量经由功率流传递的过程中不断损耗,能量密度随着与激励点距离的增加而不断衰减。功率流以激励位置为源头,流向结构内部能量密度较低的区域。结构振动的这种能量传递机制类似于热传递形式,但同时也与热传递形式存在一定区别,在热传导问题中,热能经由热对流等方式离开结构,结构本身并不耗散热能,但对于能量密度在板类结构中的分布问题,结构内的能量除可经过声辐射以及与其他结构的耦合向外传递外,结构阻尼亦耗散部分能量,当不考虑单板结构的能量流出时,外界的能量输入与阻尼耗散引起的能量损耗之间形成平衡。

图4 异形求解域的能量密度分布与能流Fig. 4 Energy density and flux of the girregular domain
2.2 线性三角形网格
更为复杂的求解域难以获得质量较高的四边形网格,若此时仍采用四边形网格,单元畸形的发生将使得计算结果误差较大,此时应该引入适应性更强的三角形网格。
对于三节点的线性三角形单元,其形函数的形式为
N=[N1N2N3]
(32)
此时可取各节点的形函数为其对应的面积坐标,如图5所示,也即
(33)
式中,Ae为三角形单元面积。
(34)
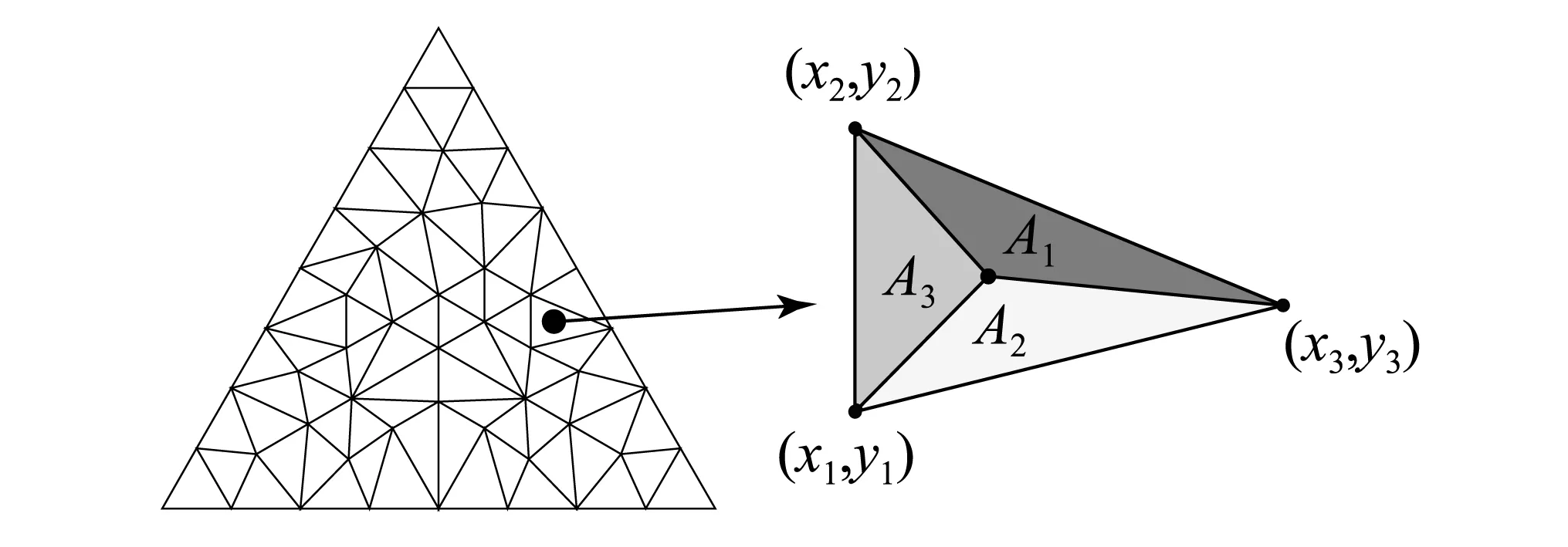
图5 薄板三角形单元与面积坐标Fig. 5 Triangle element and area coordinate
各节点所对应的面积亦可以类似求得。物理坐标下线性三角形单元的能量耗散矩阵为
(35)
利用面积坐标在三角形中的积分公式
(36)
式中,Lk为三角形单元的第k个节点所对应的面积坐标,可得
(37)
线性三角形单元的能量扩散矩阵为
(38)
线性三角形单元的应变矩阵为常数矩阵,从而式(38)为常数积分,将式(33)代入式(11)并在三角形单元内进行积分可得
(39)
其中,
(40)
(41)
(42)
式中,i,j,k取值为1, 2, 3,轮流换位,正序排列。
为验证三角形网格的适用性,再次使用三角形网格对图4中的薄板进行网格划分求解并与四边形网格以及统计能量法的求解结果进行对比。仍采用表1中的薄板参数,计算频率为1~5 kHz的1/3倍频程中心频率。由于统计能量法基于模态原理,提供的是子系统的平均能量响应,而功率流有限元方法的建立基于波动原理,得到的是具有空间分布特性的能量密度,为实现二者的对比,在将板结构视为单一子系统的情况下可将具有空间分布特性的能量密度在子系统内进行空间平均
(43)
将式(6)代入式(43)可得
(44)
式中:M为网格数目;Ni和ei分别为第i个单元的形函数以及单元节点能量密度值。图6为三者的对比结果,由图可见,使用三角形单元以及四边形单元时,功率流有限元空间平均后的能量密度皆与SEA结果吻合良好,表明三角形单元以及四边形单元在功率流有限元中具有较高的精度以及良好的收敛性。

图6 功率流有限元与统计能量法结果对比Fig.6 Comparison between results of PFFEA and SEA
三角形单元对复杂求解域具有更好的适应性,可对较为复杂的求解域进行网格离散,因此当板类结构较为复杂时,可考虑采用三角形单元进行网格划分与求解。如图7所示,以一类似于我国内陆轮廓形状的薄板为实例,该薄板与前文所分析的方形薄板具有相同的材料属性,由于其几何形状较为复杂,不适合使用四边形单元对于求解域进行离散,故选用三角形单元进行网格划分。
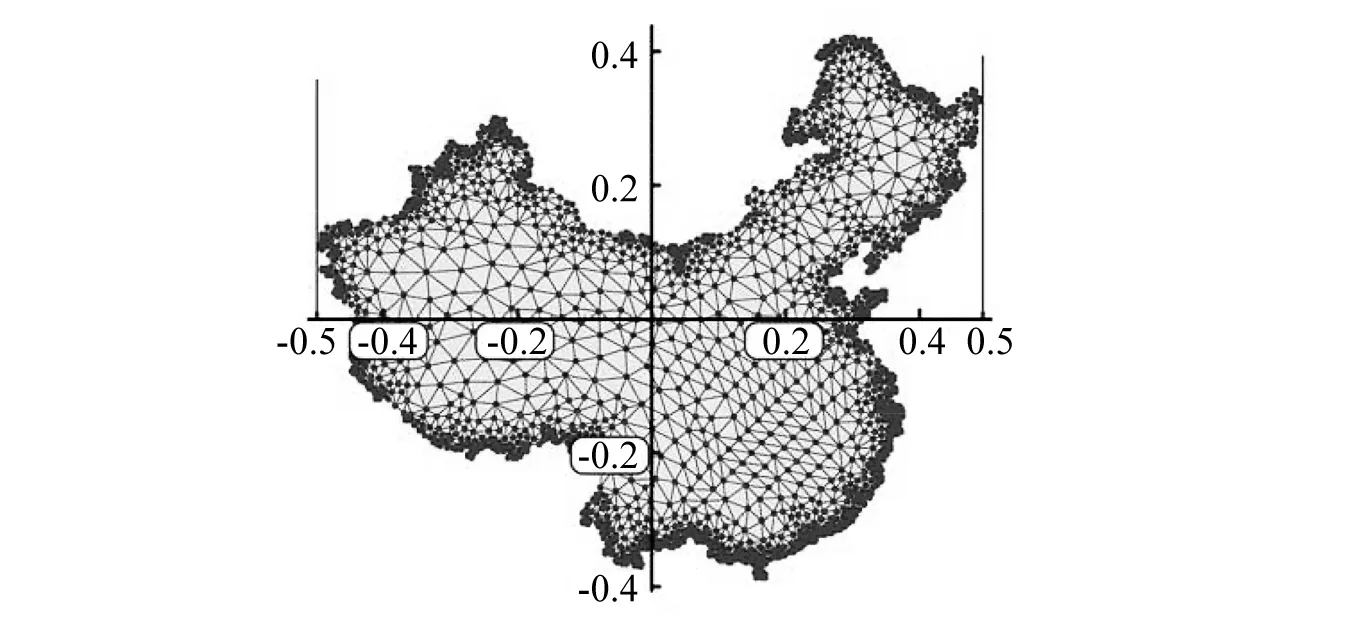
图7 三角形网格的划分(单位:m)Fig. 7 Triangular element mesh(unit:m)
利用式(37)和式(39)分别计算各个单元所对应的能量耗散矩阵与能量扩散矩阵,考虑无能量从该薄板流出的情形,则单元边界能量密度梯度有关的向量Q(e)不需计算。考虑多点激励的形式,在该薄板上选取6处位置,施加单位集中功率激励,与四边形单元求解类似,可利用δ函数表示集中功率激励,进而可求解得出外界对薄板功率输入向量。通过对单元矩阵的组装求解可得到节点处的能量密度响应。
薄板内能量密度分布如图8所示,由图可知,在集中功率输入的位置能量密度较大,各个功率输入点之间形成“能量密度峰”,在各个输入点之间,随着与功率激励点位置距离的增加,能量在传播过程中不断耗散,能量密度也随之衰减,从而在各个“能量密度峰”之间形成“能量密度谷”。
图9为该薄板能量密度分布的等高线以及功率流分布图,在多点激励情况下,板内的能量密度以激励位置为圆心呈辐射状分布。图9中左侧的两处激励位置虽与其余四处激励位置具有相同的激励,但由于右侧两处功率激励位置处能量传递影响范围较大,因此该激励点位置能量分布较为稀疏,激励点周围能量密度较小,右侧四处激励点由于能量传递影响范围较小且激励点相对集中,能量密度分布较为密集,因此激励点附近能量密度较大。在多点激励下,各个激励点为功率流的源头,功率流由各个激励点流向板内能量密度较低的区域。
薄板内的能量密度由形函数直接插值得到,而不再类似于静力学有限元求解中需使用应变矩阵以及本构关系得到单元内的应力分布,三角形单元形函数的连续性保证了单元内能量密度分布的连续性,因此不同于三角形单元在静力学有限元求解时的“常应力单元”现象,功率流有限元中所引入的三角形单元不是常能量密度单元。同时,形函数的德尔塔函数性质和单位分解性质使得能量密度在不同单元的边界保持连续。当使用三角形单元时,同样可由式(31)可确定板内的功率流分布情况,此时值得注意的是,线性三角形单元的形函数为关于坐标的线性函数,其单元应变矩阵为常数矩阵,因此在三角形单元虽不为常能量密度单元,但却为常功率流单元,当需要得到较为精确的功率流分布时,应增加三角形单元数目,或使用高次三角形单元以及四边形单元等单元类型。
3 结 论
利用功率流有限元方法对结构的振动响应进行分析具有诸多优势,本文在已有研究的基础上,利用该方法对薄板在功率激励下的能量密度的分布进行了研究,分别使用四边形单元和三角形单元对薄板结构进行网格划分,建立了对应的单元矩阵和有限元方程,求解有限元方程得出了薄板的能量密度响应。

图8 薄板内的能量分布Fig. 8 Energy density distribution of the thin plate

图9 薄板的能量密度分布与能流Fig. 9 Energy density and energy flux of the thin plate
四边形单元可对应用广泛的矩形薄板进行网格划分求解,同时当求解域非矩形但划分得到的四边形单元畸形程度较低时仍可使用四边形单元。当求解域较为复杂时,应使用三角形单元对薄板进行网格划分时。三角形单元的引入可将功率流有限元法拓展至任意形状的薄板类结构,同时三角形单元内的能量密度由形函数插值得到,因此在功率流有限元中利用三角形单元得到的能量密度连续分布,并不出现“常能量密度单元”。三角形单元为常功率流单元,因此当需要得到较为详细的功率流分布时,应使用较为细密的三角形网格或采用其他单元类型。多种单元类型的使用可有效的将功率流有限元方法应用于异形薄板以及复杂耦合板结构。
[ 1 ] 宋孔杰,张蔚波,牛军川. 功率流理论在柔性振动控制技术中的应用与发展 [J]. 机械工程学报, 2003, 39(9): 23-28. SONG Kongjie, ZHANG Weibo, NIU Junchuan. Application and development of power flow theories in the field of the vibration control for flexible system [J]. Chinese Journal of Mechanical Engineering, 2003, 39(9): 23-28.
[ 2 ] CHO P E. Energy flow analysis of coupled structures [D]. United States: Purdue University, 1993.
[ 3 ] 朱继清. 基于能量流有限元的耦合结构振动传递特性分析 [D]. 济南:山东大学, 2011.
[ 4 ] NEFSKE D J, SUNG S H. Power flow finite element analysis of dynamic systems: basic theory and application to beams [J]. Journal of Vibration & Acoustics, 1989, 111(1): 94-100.
[ 5 ] WOHLEVER J C, BERNHARD R J. Mechanical energy flow models of rods and beams [J]. Journal of Sound and Vibration, 1992, 153(1): 1-19.
[ 6 ] CHO P E, BERNHARD R J. Energy flow analysis of coupled beams [J]. Journal of Sound and Vibration, 1998, 211(4): 593-605.
[ 7 ] SONG J H, HONG S Y, KANG Y, et al. Vibrational energy flow analysis of penetration beam-plate coupled structures [J]. Journal of Mechanical Science and Technology, 2011, 25(3): 567-576.
[ 8 ] BOUTHIER O M, BERNHARD R J. Simple models of energy flow in vibrating membranes [J]. Journal of Sound and Vibration. 1995, 182(1): 129-147.
[ 9 ] BOUTHIER O M, BERNHARD R J. Simple models of the energetics of transversely vibrating plates [J]. Journal of Sound and Vibration, 1995, 182(1): 149-166.
[10] PARK D H, HONG S Y, KIL H G, et al. Power flow models and analysis of in-plane waves in finite coupled thin plates [J]. Journal of Sound and Vibration, 2001, 244(4): 651-668.
[11] 李坤朋. 基于能量有限元法的板耦合结构振动特性分析 [D]. 济南:山东大学, 2013.
[12] NIU Junchuan, LI Kunpeng. Energy flow finite element analysis of L-shaped plate including three types of waves [J]. Applied Mechanics and Materials, 2013, 353/356: 3365-3368.
[13] NIU Junchuan, LI Kunpeng. Energy finite element analysis of n-shaped plate structures with three types of wave [J], Journal of Vibration Engineering and Technologies, 2015, 3(5): 615-625.
[14] 江民圣,牛军川,郑建华,等. L 型耦合板结构能量传递系数特性的研究 [J]. 振动与冲击, 2015,34(17): 131-136.JIANG Minsheng, NIU Junchuan, ZHENG Jianhua, et al. Energy transfer coefficients features of L-shape coupled plates [J]. Journal of Vibration and Shocks, 2015, 34(17): 131-136.
[15] SEO S, HONG S, KIL H. Power flow analysis of reinforced beam-plate coupled structures [J]. Journal of Sound and Vibration. 2003, 259(5): 1109-1129.
[16] PEREIRA V S, DOS SANTOS J M C. Coupled plate energy models at mid-and high-frequency vibrations [J]. Computers & Structures, 2014, 134(4): 48-61.
Energy density analysis of irregular shaped plates based on the power flow finite element method
LIU Zhihui1, NIU Junchuan1,2, ZHOU Yiqun1
(1. School of Mechanical Engineering, Shandong University, Ji’nan 250061, China; 2. Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Shandong University, Ji’nan 250061, China)
It has important significance to analyze and predict the vibration response of structures under different frequencies. The power flow finite element method has become a research focus for vibration analysis due to the advantages of broad applicable frequency range and the detailed information provided. The power flow finite element method was implemented to solve the flexural wave energy density of a thin plate, and the weighted residual method was used to derive the residual of the node points. The linear quadrilateral mesh was used to partition the thin plate and the element’s finite element equation was derived, then the global finite element equation was assembled and solved, and the energy density of the nodes was obtained. The linear triangular element was introduced to partition the plate with complex shape. The research is meaningful for the implementation of the power flow element method on thin plates with arbitrary shapes.
vibration; power flow finite element analysis; irregular shaped plate; energy density
国家自然科学基金(51275275;51675306);山东省优秀中青年科学家科研奖励基金(BS2010ZZ006)
2016-01-19 修改稿收到日期: 2016-06-17
刘知辉 男,硕士,1992年7月生
牛军川 男,教授,博士生导师,1974年生
TH212;TH213.3
A
10.13465/j.cnki.jvs.2017.16.029

