基于最短增广链的最大流改进算法
赵礼峰,纪亚劲
(南京邮电大学 理学院,江苏 南京 210023)
基于最短增广链的最大流改进算法
赵礼峰,纪亚劲
(南京邮电大学 理学院,江苏 南京 210023)
网络最大流是经典的组合优化问题,它的经典算法主要有三种,分别是Ford-Fulkerson算法、最短增广链算法(Dinic算法)和预流推进算法。Ford-Fulkerson算法中由于增广链的选取任意性而有时无法得到理想的最大流。最短增广链算法在分层剩余网络中寻找最短增广链,从而避免了增广链选取的任意性。但最短增广链算法在求解最大流过程中每次增广都需要重新寻找最短增广链,利用率不高。针对这一问题,提出了一种修复最短增广链的新算法。该算法在沿最短增广链调整流量之后,删除最短增广链流量为零的弧,且寻找合适的路径修复最短增广链,从而提高了最短增广链的使用效率,减少了最短增广链的搜索次数。应用新算法进行了BA无标度网络建模仿真。实验结果表明,该算法运行效率要高于最短增广链算法。
最大流;分层剩余网络;最短增广链;BA无标度网络
0 引 言
网络最大流问题是图论中极其重要的分支,是经典的组合优化问题,也可以看成特殊的线性规划问题[1]。它在运筹学、计算机、工程等众多科学领域中有着广泛的应用[2-3],例如,运输问题、分派问题、通信问题等都可以转化为网络最大流模型来解决。因此,研究网络最大流算法具有很重要的意义。
至今为止,网络最大流问题的研究已经有50多年的历史,现已建立了较为完善的理论并且提出了一系列经典算法。如1956年提出的Ford-Fulkerson算法[4],随后Dinic,Edmonds和Karp对Ford-Fulkerson算法进行了改进,提出了最短增广链算法[5-6]。该算法提出了分层剩余网络的概念,其主要思想是每次都是沿着最短增广链进行增广。1986年,Karzanov提出了预留推进算法[7],Goldberg和Tarjan对此进行了深入研究并提出了一系列的改进算法[8-9];另外,还有大量的学者针对一些特殊网络提出了自己的算法[10-16],这些算法是如今研究大规模网络的基础。
Ford-Fulkerson算法的优点是适用度广,但是每次都是任意寻找增广链,使得算法复杂度偏高;最短增广链算法在Ford-Fulkerson算法的基础上改进很多,即沿着最短增广链进行增广,在很大程度上降低了复杂度。但是算法仍存在缺陷,由于每次沿最短增广链增广之后需重新寻找最短增广链,所以利用率不高。
针对上述不足,提出了一种新的改进的最短增广链算法。该算法通过一种方法来修复最短增广链[17],避免了反复重新寻找新的最短增广链,以提高算法效率。
1 基本概念
1.1 最大流的数学模型
给定一个容量网络G=(V,A,c),其中V是顶点集,A是弧集,c是弧的容量,f(a)(a∈A)称为通过弧a的流量。在网络G中定义两个顶点vs和vt,vs为G的发点,vt为G的收点。
网络最大流模型:

1.2 分层剩余网络
对于一个容量网络G=(V,A,c)及G上的可行流f,令
称A+(f)为前向弧集,A-(f)为后向弧集,且记A+(f)∪A-(f)=A(f),令
称cij(f)为弧(vi,vj)关于f的剩余容量。
定义1:由V,A(f)和c(f)组成的网络G(f)=(V,A(f),c(f))称为网络G关于f的剩余网络。
定义2:对于剩余网络G(f)=(V,A(f),c(f)),规定关于G(f)的子网络AG(f)=(V'(f),A'(f),c(f)),如下:
V'(f)={vt}∪{vi∈V|h(vi) A'(f)={(vi,vj)∈A(f)|h(vj)=h(vi)+1 则AG(f)称为G的关于f的分层剩余网络[18]。 2.1 算法思想 首先从容量网络D的任一个可行流f1(例如零流)开始,构造G的关于f1的分层剩余网络AG(f1),在AG(f1)中使用深度优先搜索算法选取一条(vs,vt)路径P1,沿P1对f1进行增广,并相应修改P1上的容量,在AG(f1)中删去P1上容量为零的弧,且同时在原网络中删去相应的弧,然后对P1进行修复,修复的方法是:从发点vs和收点vt出发,沿P1向中间逐点遍历,若遇断点便停止遍历并分别记为断点vi和vj,考察在AG(f1)中是否存在从vi到vj的路径,若存在,则修复最短增广链P1,继续沿P1对f1进行增广,直至不能修复,如图1所示。之后在AG(f1)中重新选取增广链P2,重复上述操作。经过有限次增广,使得余下网络不再有(vs,vt)路径,从而得到新的可行流f2。vt在G(f2)中的层数大于vt在G(f1)中的层数,重新构造分层剩余网络AG(f2),对于AG(f2)重复以上的做法,得到可行流f3,一直做下去,直到得到可行流fk,使得G(fk)中不存在(vs,vt)路径,此时fk即为G的最大流。 图1 最短增广链修复过程 定理1:分层剩余网络AG(f)中(vs,vt)路就是容量网络G中关于f的最短增广链。若沿着最短增广链增广后,通过该方法修复的路径仍为最短增广链。 证明:增广链的定义是,对于G中一条(vs,vt)链P,若P的前向弧为f非饱和弧,后向弧为f正弧,则称P为关于f的(vs,vt)的增广链。 由剩余网络的定义知,剩余网络中弧的容量为: 设P是剩余网络G(f)中的一条(vs,vt)路,则P中任一条弧都满足增广链的定义。 又根据分层的规则易知,G(f)中任何最短(vs,vt)路都在AG(f)中,且AG(f)中任何(vs,vt)路都是G(f)的最短(vs,vt)路,即AG(f)中任何(vs,vt)路都是容量网络G中的最短增广链。而通过该算法修复的路径仍是AG(f)中的(vs,vt)路径,所以修复的路径仍是最短增广链。 2.2 算法步骤 最大流算法: 输入:原容量网络G=(V,A,c)与指定的发点vs、收点vt; 输出:最大流f。 Step1:在G中取初始可行流f1(可以取零流),令k=1。 Step2:先构造剩余网络G(fk),再利用广探法构造分层剩余网络AG(fk),若AG(fk)中vt得不到标号,结束,fk就是G的最大流,否则转Step3。 Step3:在AG(fk)中寻找(vs,vt)路P(深度优先原则),转Step4,若不存在,则令fk+1=fk,k=k+1,转Step2。 Step4:沿P对fk进行增广,相应修改AG(fk)中P上弧的容量,删去P上容量为零的弧和原网络中相应的弧。 Step5:对增广链P进行修复,转Step4,若不能修复,转Step3。 2.3 算法可行性分析 该算法运行时,每次在分层剩余网络中找到或修复一条最短增广链后,都从发点vs出发沿不饱和弧进行增广,一直推进到收点vt,增广后最短增广链上至少有一条饱和弧。设网络G=(V,A,c)中共有m条弧,那么该算法最多经过m次增广后,网络G饱和,此时网络G无法找到或修复一条最短增广链,算法终止,得到网络最大流。所以该算法会在有限的步骤之后终止。 2.4 算法复杂度分析 设G的顶点数为n,弧数为m。因为算法中构造的分层剩余网络AG(fk)的层数随着k单调增加,所以Step2中构造分层剩余网络AG(fk)最多执行n-1次,又由广探法知,每次构造分层剩余网络AG(fk)的复杂度为O(m)。在AG(fk)中寻找增广链后都要删去至少一条弧,所以至多找m次(vs,vt)路,每次寻找(vs,vt)路的计算量为O(n),于是得到算法的时间复杂度为:O(n+n·m+n·n·m)=O(n2m)。 在改进算法运行过程中,Step5中每一次对最短增广链进行修复,就减少了在AG(fk)中最短增广链的搜索次数,最终降低了时间复杂度。 例:求图2中从vs到vt的网络最大流。 解:(1)对于网络G,取零流f1作为初始可行流,令k=1。 (2)构造剩余网络G(f1),然后利用广探法构造AG(f1),见图3。 图2 容量网络G 图3 分层剩余网络AG(f1) (3)在AG(f1)选取最短增广链P1=vsv1v2v3vt,δ=min{5,1,1,6}=1,沿P1对f1进行增广流值1,得到新的可行流仍记为f1,修改AG(f1),删去AG(f1)和原网络中的弧(v1,v2),(v2,v3)。 (4)对最短增广链P1进行修复,断点为v1,v3,修复后的最短增广链为P1=vsv1v5v3vt,δ=min{4,6,3,5}=3,沿P1对f1进行增广,流值为3,得到的可行流仍记为f1,修改AG(f1),删去AG(f1)和原网络中的弧(v5,v3)。 (5)对于最短增广链P1=vsv1v5v3vt不能修复,则转到步骤(3)重新寻找最短增广链,并且在之后的步骤中不需要进行修复,所以之后的算法执行情况和最短增广链算法相同。最后得到容量网络G的最大流f2,且最大流流值为v(f2)=9,见图4。 图4 最大流f2 为比较改进算法与最短增广链算法的运行时间,分别在网络规模为300,600,900,1 200,1 500,1 800个节点的BA无标度网络上进行仿真比较,编程环境为Matlab2012b。 BA无标度网络邻接矩阵生成过程如下: (1)先使用p=0.5的概率生成一个规模为50×50的完全随机网络,并用0表示对应的弧不存在,1表示对应的弧存在; (2)求出邻接矩阵的行和作为每个节点的度数; (3)新增节点,并且给每个新增的节点生成50条边; (4)计算节点度数累计概率并用赌轮法将新增节点与原有网络节点连接并更新邻接矩阵,直到达到给定的规模停止更新; (5)将BA无标度网络邻接矩阵中数值为1的元素替换为一定范围内的随机数作为弧容量。 对于每种规模,进行5次仿真实验,然后取平均运行时间进行比较,结果见表1。 表1 两种算法在不同规模网络上的实验结果 从表1中可以看出,改进算法和最短增广链算法同样都能精确地求出网络最大流,并且改进算法的运行速度比最短增广链算法快。 两种算法的平均运行时间对比曲线如图5所示。 图5 两种算法的平均运行时间 从图5中更能明显看出,改进算法的运行效率比最短增广链算法高,并且节点数也多,优化的效率更明显。所以对于大型网络新算法的适用性更强。 网络最大流在众多领域中应用广泛,而最短增广链算法是求解网络最大流问题的经典算法之一。与Ford-Fulkerson算法相比,其避免了增广链选取的任意性,从而减少了算法复杂度。但最短增广链算法在求解最大流的过程中,每条最短增广链只能增广一次,效率较低。文中提出的改进算法通过修复最短增广链提高了最短增广链的使用效率。仿真结果表明,该算法与其他最短增广链算法相比,在不同规模的随机网络中运行速度都较快,因此求解网络最大流的效率更高。 [1] 张宪超,陈国良,万颖瑜.网络最大流问题研究进展[J].计算机研究与发展,2003,40(9):1281-1292. [2] Pardalos P M,Resende M G C.Handbook of applied optimization[M].New York:Oxford University Press,2002:363-374. [3] Schrijver A.On the history of the transportation and maximum flow problems[J].Mathematical Programming,2002,91(3):437-445. [4] Ford J L R,Fulkerson D R.Maximum flow through a network[J].Canadian Journal of Mathematics,1956,8(5):399-404. [5] Edmonds J,Karp R M.Theoretical improvements in algorithmic efficiency for networks flow problems[J].Journal of ACM,1972,19(2):248-264. [6] Dinic E A. Algorithm for solution of a problem of maximum flow in a network with power estimation[J].Soviet Mathematics Doklady,1970,2(5):1277-1280. [7] Karzanov A V.Determining the maximum flow in a network by the method of pre-flows[J].Soviet Mathematics Doklady,1974,15(3):434-437. [8] Goldberg A V.The partial augment-relabel algorithm for the maximum flow problem[C]//European symposium on algorithms.Berlin:Springer,2008:466-477. [9] Goldberg A V,Rao S.Beyond the flow decomposition barrier[J].Journal of ACM,1998,45(5):783-797. [10] 张宪超,陈国良.小容量网络上的最大流算法[J].计算机研究与发展,2001,38(2):194-198. [11] 邱伟星,王以凡,沈金龙.一个求无向网络最大流的算法[J].南京邮电学院学报,1997,17(4):170-172. [12] 郭 强.无向网络最大流问题研究[J].计算机工程与应用,2005,41(9):76-78. [13] Weihe K.Maximum (s,t)-flows in planar networks in O(|V|log|V|)-time[J].Journal of Computer System Science,1997,55(3):454-476. [14] Borradaile G,Klein P.An O(nlogn) algorithm for maximum st-flow in a directed planar graph[J].Journal of ACM,2009,56(2):524-533. [15] Negruseri C S,Pasoi M B,Stanley B,et al.Solving maximum flow problems on real world bipartite graphs[J].Journal of Experimental Algorithmics,2011,16(3):14-28. [16] Erickson J.Maximum flows and parametric shortest paths in planar graphs[C]//ACM-SIAM symposium on discrete algorithms.Austin,Texas,USA:ACM,2010:794-804. [17] 赵礼峰,严子恒.基于增广链修复的最大流求解算法[J].计算机应用,2015,35(5):1246-1249. [18] 谢 政.网络算法与复杂性理论[M].长沙:国防科技大学出版社,2003. Improved Algorithm of Maximum Flow with Shortest Augmenting Chain ZHAO Li-feng,JI Ya-jin (College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China) The maximum network flow is a classic combinatorial optimization problem,which mainly consists of Ford-Fulkerson algorithm,the shortest augmenting chain algorithm (Dinic algorithm) and preflow push algorithm.The desired maximum flow from Ford-Fulkerson algorithm could not be acquired because of the arbitrariness when choosing the augmented chain.The shortest augmenting chain algorithm can find the shortest augmenting chain in the remaining layered network to avoid the augmented chain selected arbitrary,however,it needs to search again shortest augmenting chain in maximum flow when augmenting with low using rate.Aimed at this problem,a new shortest augmenting chain repair algorithm is presented.After it has adjusted flow along the shortest augmenting chain the arc of zero flow on the augmented chain has been removed to retain the arc that the flow zero,which select the appropriate nodes to repair shortest augmenting chain in the remaining nodes for improving the efficiency and reducing the times of search shortest augmenting chain.The improved algorithm is verified through the modeling and simulation experimental in BA scale-free network,which shows that its efficiency is higher than the shortest augmenting chain algorithm. maximum flow;remaining layered network;shortest augmenting chain;BA scale-free network 2016-08-18 2016-11-23 网络出版时间:2017-07-05 国家自然科学基金青年基金项目(61304169) 赵礼峰(1959-),男,教授,硕士研究生导师,研究方向为图论及应用、矩阵论;纪亚劲(1991-),男,硕士研究生,研究方向为图论及其在通信中的应用。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1650.040.html TP301.6 A 1673-629X(2017)08-0088-04 10.3969/j.issn.1673-629X.2017.08.0182 一种改进的最大流算法
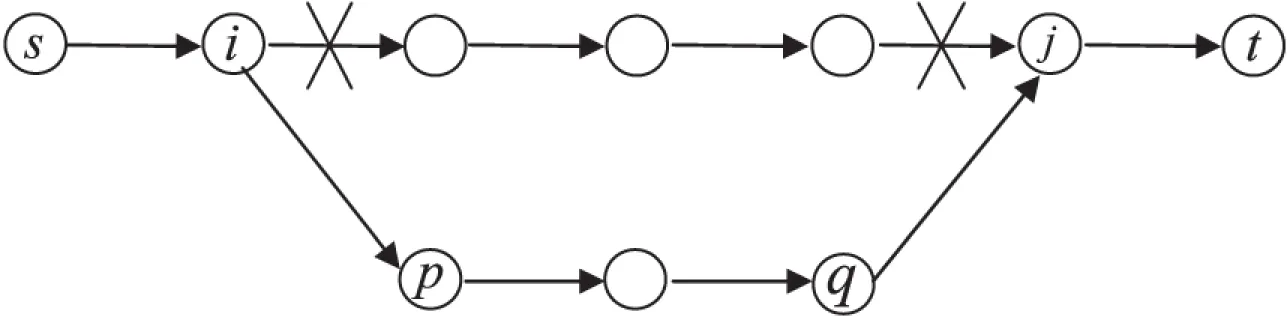
3 实例分析
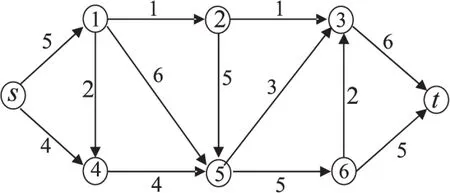


4 算法的仿真与分析


5 结束语

