矢量基尔霍夫公式经典证明的漏洞与新的严格证明∗
黄晓伟 盛新庆
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
矢量基尔霍夫公式经典证明的漏洞与新的严格证明∗
黄晓伟 盛新庆†
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
(2017年2月23日收到;2017年6月3日收到修改稿)
矢量基尔霍夫积分公式是电磁理论的一个重要公式,更是光学衍射理论的基础.然而,我们发现经典著作中这个公式的证明普遍存在漏洞.本文将逐一指出这些漏洞,在此基础上给出一个新的严格证明.最后用数值实验验证我们的结论.
矢量基尔霍夫积分,Stratton-Chu公式,Sommerfeld辐射条件
1 引 言
矢量基尔霍夫积分公式表明,空间中任意封闭曲面外一点处的电(磁)场可由曲面上电(磁)场及其法向导数积分表示出来.该公式不仅是电磁场散射理论中的一个重要公式,更是光学衍射理论的基础[1−9].然而,一直以来,国内外著作关于这个公式的证明过程都有缺陷.该公式的证明最早由麻省理工大学Kong教授[10]给出,其基本思路是,从Stratton-Chu公式出发,利用矢量恒等式和积分公式予以推导.与Kong思路类似的证明还有:西安电子科技大学葛德彪教授的证明[11],南京大学张善杰教授的证明[12]等.与此思路不同的证明还有:直接从无源Maxwell方程组出发,运用格林定理推导出标量基尔霍夫积分公式,进而导出矢量基尔霍夫积分公式[13].深入探究证明过程和积分公式的物理含义,我们发现这些经典证明过程并非很严格,甚至存在明显的漏洞.
本文以下分为三个部分:第2部分逐个指出这些经典证明的漏洞;第3部分给出一个新的严格证明;第4部分将通过一个数值算例验证我们的结论.
2 矢量基尔霍夫积分公式经典证明及漏洞
本节将给出国内外经典著作中关于矢量基尔霍夫公式的证明,并逐一指明其漏洞.
2.1 K ong著作中的证明及漏洞
Kong[10]著作中的证明是从Stratton-Chu公式出发的.我们知道,Stratton-Chu公式可以表述为
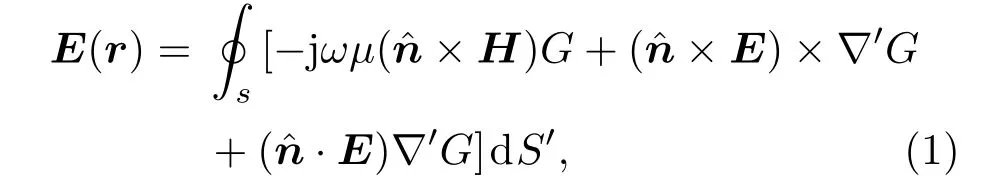
其中,E(r)是源J,M在自由空间产生的电场;G(r,r′)=,R=|r−r′|;S为如图1所示的包围所有辐射源的一个封闭曲面;r′为曲面S上任意一点,r位于曲面外部无源空间中,为曲面S外法矢.公式表明,如果把包含辐射源的区域用一个封闭曲面S包围,那么只要知道曲面上的场量,结合格林函数,可以求得辐射源外无界均匀空间任意一点的辐射场.

图1 Stratton-Chu公式模型Fig.1.Model for Stratton-Chu forMu la.
将法拉第定律代入(1)式的Stratton-Chu公式,利用矢量恒等式(×E)×∇′G=E(.∇′G)−(E.∇′G)可得

而文献[10]认为∇′算子仅作用于r′上,与法向量无关,故上式可写为

由于S面上没有自由电荷,即∇′.E(r′)=0,从而

将(4)和(5)式代入(2)式,可得
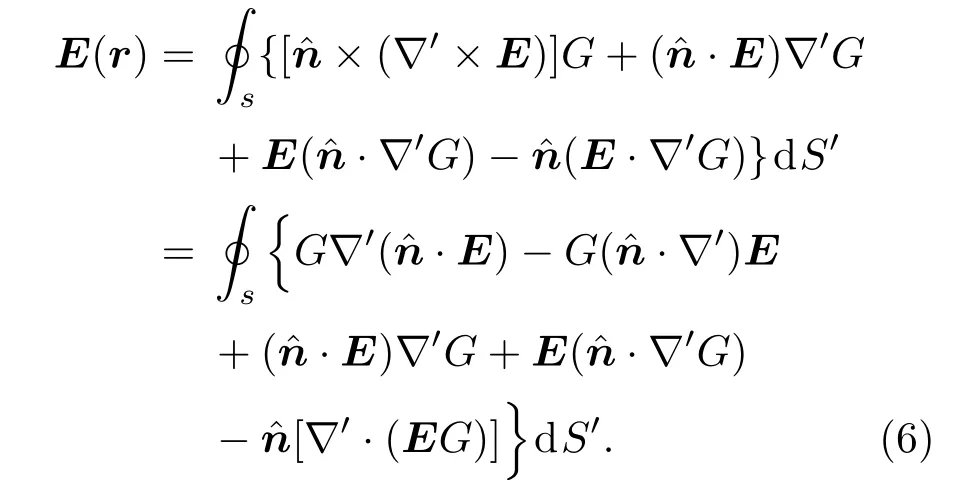
利用算子恒等式∇(fg)=g∇f+f∇g,有

将(7)式代入(6)式可得
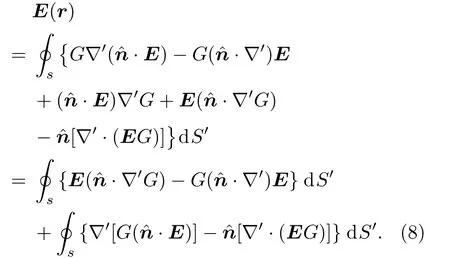
从(8)式出发,文献[10]采用张量演算中的高斯定理,证明上式第二项面积分为0.这项面积分两部分的第i分量可分别写为

将(9)式,(10)式代入(8)式,即可得到

分析上述过程,可以发现证明存在漏洞.我们知道,Stratton-Chu公式被积函数中的电场和磁场被视为源,它们都是r′的函数.表述它们切向和法向的单位矢量自然也是r′的函数.因此,∇′算子作用在不为零,即对于∇′不能再作常矢(后面数值算例会进一步清晰展示这一点).这样,(4)式就不能成立,由此为基础的(8)式的第二个等号自然是错误的.另外,由于为r′的函数,不是常矢量,(9)式的第二个等号也不能成立,这是由于其nj不能提出来放入d S′,导致不满足高斯定理使用条件.从而上述导出矢量基尔霍夫积分公式的过程是存在漏洞的.
2.2 葛德彪著作中的证明及漏洞
葛德彪著作中的证明也是基于Stratton-Chu公式[11].与2.1节思路类似,(8)式以前的推导过程一致.注意到,葛德彪[11]也认为,∇′与法向量无关,此时有下式成立:
将(12)式代入(8)式可得

将封闭曲面S划分为如图2所示两个部分.

图2 Stokes定理应用示意图Fig.2.DiagraMfor the app lication of Stokes theorem.

上式最后一个等号成立,是因为回路L1,L2分别为曲面S1,S2的边线,两项积分彼此相消.将(14)式代入(13)式,从而也可得到



图3 光学中平面屏幕衍射的基尔霍夫近似公式Fig.3.K irchhoff app roxiMation forMu lation of d iff raction by a p lane screen for op tics.
2.3 张善杰著作中的证明及漏洞
张善杰[12]著作给出的证明过程如下:
从(2)式出发,因−jωµH= ∇′×E+Jm,(2)式被积函数第一项可以写为
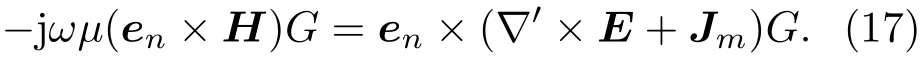
运用矢量恒等式:∇′×(u A)=u∇′×A−A×∇′u和a×b×c=(a.c)b−(a.b)c,被积函数第一项可写为

再次运用三矢量的叉积恒等式,(2)式积分内被积函数的第二、三项之和可以表示为


由于在曲面S上无源,ρ=0,Jm=0,于是(24)式可以简化为
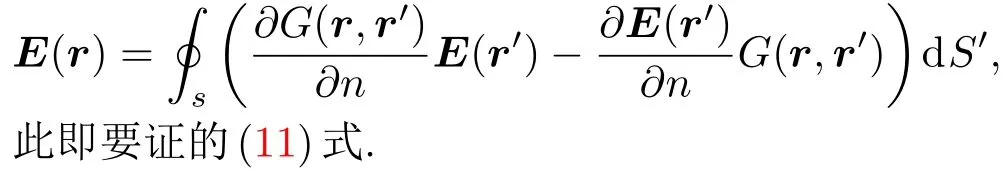
上述证明与葛德彪和孔金瓯的证明都不同,没有用到环路积分定理和高斯积分定理,而是将场量分解为三个直角坐标分量,再重新组合.证明中的漏洞主要在以下两个问题.
第一个问题:(19)式的第一个等号是否成立?
以其中一项(en.ex)∇′Ex为例,根据梯度定义(,方向指向)Ex增长最快,然而经过第一个等号,(en.ex)en方向将指向积分表面的外法向量,这两者方向显然不是在曲面任何一点都成立的.这也直接导致(21)式不成立.
第二个问题:(23)式的第二个等号,也取其中一项分析,(en.E)∇′G明显不会等于(en.E)en.因为,如图1所示,∇′G的方向为,则是积分曲面的外法向量,两者明显不共线.
这两个问题可以综合为以下描述:设ψ为一个标量函数,那么有但是,∇ψ=却是有条件的,除非ψ增长最快的方向与共线.
2.4 杨儒贵著作中的证明及缺失
杨儒贵[13]著作中证明直接从Maxwell方程入手,在无源区域求解齐次矢量亥姆霍兹方程,这也是其他国外教材的典型证明.以下为文献给出的过程.
如图4所示,设全部辐射源被闭合曲面S0包围,在S0外再做一个曲面S1,在S0和S1之间为无源区.
由电流和磁流共同产生的电磁场满足以下Maxwell方程:

在无源区,上式可以化为下列齐次矢量亥姆霍兹方程:


图4 Maxwell场方程的积分Fig.4.The integral of electric field in Maxwell’s equations.
在直角坐标系,电场强度的每一个分量U(r)均满足以下标量齐次亥姆霍兹方程:

其中,U(r)代表电场强度任意一个直角坐标分量.要求解微分方程(27),还需要知道边界条件.现假设已知S0和S1上的场量作为边界条件.那么对于S0和S1两个闭合面包围的无源区,齐次标量亥姆霍兹方程可由标量格林定理解出:

由于惟一性要求,需要讨论无穷远处的标量场性质,这需要在无穷远处对辐射场做一些额外的假设,这就是

将S1推向无穷远处,即S1→∞,此时求解空间为无源无穷空间.文献[13]认为,由辐射条件(29),可知
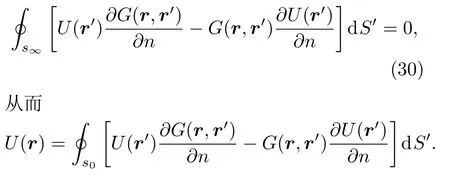
这就是标量基尔霍夫积分公式.
既然每一个直角坐标分量都满足上式,那么三个直角坐标分量相加以后,可得到与(11)式完全一样的矢量基尔霍夫积分公式:

分析上述过程,可以发现,(29)式是直接利用的,并未证明.实际上,经过严格证明的电磁场能够满足的辐射条件为以下形式[15]:

那么,能否从(31)式导出(29)式所示的辐射条件呢?答案是否定的.从(31)式可以看出旋度和叉积操作已经把三个直角坐标分量U(r)耦合在一块,无法直接分离为(29)式所示的三个直角坐标分量.所以从(31)式,无法导出(29)式.从而也推导不出(30)式和(11)式,这正是文献[13]证明的缺失.
那么(29)式是否成立呢?实际上,Sommerfeld[16]将(29)式仅作为一个条件提出,实际中电磁场是否满足此式一直没有很严格的推导.文献[17,18]给出了(29)式成立的一些前提,但都没有给出满足这些前提的证明.附录A将从电场远场近似出发试图给出(29)式一个严格证明作为杨儒贵[13]证明的补充.
3 严格证明
由第2部分可以发现,经典著作中证明矢量基尔霍夫积分公式的过程都有漏洞或者缺失.基于对上述证明过程的分析,本部分我们将给出一种矢量基尔霍夫积分公式的严格证明.
证明之前,先给出两个引理.由于以下要用到张量,我们先给HaMilton算子做一个普适的符号说明[19]:

(32)式中,采用爱因斯坦求和约定,其中,gi为逆变基矢量,◦表示点积、叉积或并积,φ可以代表标量,也可以表示矢量或者张量.
引理1 采用上述的符号说明,以矢量场的高斯公式为基础,可以有以下高斯定理的推广形式:

引理2 对于矢量的拉普拉斯算子,存在以下等式:

两个引理的证明可以参见附录B.
下面证明矢量基尔霍夫(11)式.将(3)式代入(2)式,并且注意到∇′.E(r′)=0,可以得到

要证矢量基尔霍夫积分,也即证(35)式后面两项面积分为0.由矢量恒等式有:


运用引理1,上式的第二个面积分三项可以化为体积分:

将(38)式代入(37)式,再注意到引理2的矢量恒等式,可知

从而矢量I基 (尔霍夫积分公式得证.

若要得到标量形式的基尔霍夫积分,直接将矢量式分解为三个直角坐标分量即可.
4 数值实验
第2部分所述几种证明漏洞都是在于证明(35)式面积分第二、三项为分别0:

然而第3部分我们的证明指出,事实上(35)式的第二、第三项面积分之和为0,而它们各自却不一定为0.我们将设计一个数值实验证明我们的论证.
作为最简单的源,我们以赫兹偶极子辐射场为例.位于原点的赫兹偶极子J=ez产生的辐射场为

将(40)式代入(39)式,为了便于分析,我们设积分曲面为一个包围偶极子的球面,其方程为

其中,r′作为球面的半径用作仿真输入参数.将矢量积分分解为三个直角坐标标量积分,即

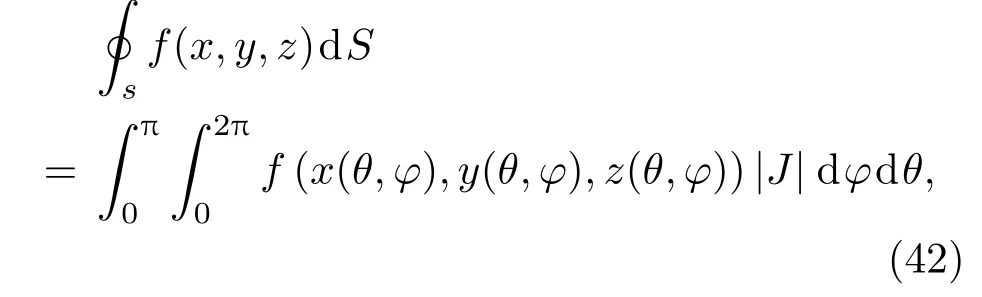
其中,|J|为坐标变换的Jacobi行列式,对于球面而言

为提高运行速度,采用如图5所示的积分方法:将大的矩形划分为一个个小的矩形,采用中点的值代替四个角点的平均值进行梯形法数值积分.
表1展示了在频率为300 MHz时,(39)式两项矢量积分在三个直角方向分量模值随着不同分割精细度下的积分结果.结果表明,积分随着网格变密是收敛的.从表1可以看出,(39)式的三个方向的积分结果并不是都为0的.其中,Int1,Int2两者的x,y方向积分显然不为0,这充分说明,前面所述经典著作中的证明确实存在漏洞.

图5 二重积分的数值积分模型Fig.5.NuMerical integralModel for doub le integral.

表1 观测点为r=(5,5,5),球面半径为1,不同积分精细度下电场模值的收敛情况Tab le 1.Convergence of E lectric Field Modu lus under d iff erent integral steps,When observation coordinates is r=(5,5,5)and the spherical radius is equal to 1.
更重要的一点是,从表1我们可以看出,虽然Int1,Int2两者的积分各自不为0,但是两者之和确实为0,随着积分网格密度变大,Int1,Int2两者之和的模值在三个方向都有收敛到0的趋势,这也进一步验证了我们的证明.
5 结 论
本文详细分析了矢量基尔霍夫公式的多个经典证明过程,并逐一指出了证明中的漏洞.漏洞之源有二:1)Stratton-Chu公式中积分曲面的法向量被当成常矢量;2)误以为矢量Sommerfeld辐射条件可以在直角坐标系下分离.本文通过引入HaMilton算子,运用高斯定理的推广形式及矢量拉普拉斯算子恒等式,重新给出了矢量基尔霍夫公式的一个严格证明,并通过数值算例验证我们的发现和证明.
附录A 证明任何辐射源满足标量Sommerfeld辐射条件
任何单一频率激励源,有以下远场近似[20]:

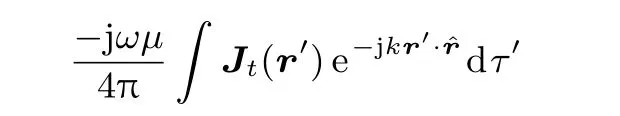
仅与角度θ,φ有关,将(A 1)式化为直角坐标分量,其第i个分量可以表示为
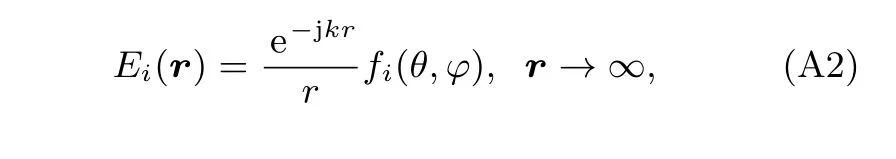

容易发现,fi(θ,φ)事实上是Jt(r′)从空间域到角域的傅里叶变换,实际中,源总是分布在有限空间,且功率有限,其变换域在每个角度也是有限大的值,也即,|fi(θ,φ)|<∞,∀θ,φ,从而可以知道

现在我们将证明U(r)=Ei(r)满足

其中,值得注意的是法向量的方向是容易理解错的.这里由于研究场点,从而法矢沿曲面向外.
当r→ ∞可知r→ R=|r−r′|,从而由(A 2)和(A 4)式可得

从而正文中(29)式标量辐射条件对任意直角坐标分量成立.将(29)式的 r换为r′,即可推出(30)式.以上是对杨儒贵著作证明的一个补充.
附录B 两个引理的证明
引理1的证明中,我们选取φ为标量以及张量予以证明,其他情况可以类推.
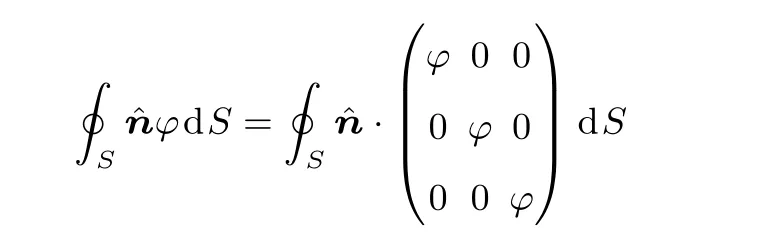

[1]Jackson J D 1998 C lassical E lectrodynaMics(3rd Ed.)(NeWYork:Wiley-Interscience)pp479–482
[2]Born M,Wolf E 1986 Principles of Optics(6th Ed.)(NeWYork:PergaMon Press Ltd)pp375–378
[3]Buchwald J Z,Yeang C P 2016 Arch.Hist.Exact Sci.70 463
[4]Wang X F,Wang J Y 2011 Acta Phys.Sin.60 025212(in Chinese)[王晓方,王晶宇 2011物理学报 60 025212]
[5]Gordon WB 1975 IEEE Trans.An tennas Propagat.23 590
[6]UMu l Y Z 2013 Opt.ComMun.291 48
[7]Wang A,Prata A 1995 Opt.Soc.Am.A 12 1161
[8]Liu C X,Cheng C F,Ren X R,Liu M,Teng S Y,Xu Z Z 2004 Acta Phys.Sin.53 427(in Chinese)[刘春香,程传福,任晓荣,刘曼,滕树云,徐至展 2004物理学报 53 427]
[9]Sheng X Q 2016 E lectroMagnetic Theory,CoMputation,Application(Beijing:H igher Education Press)pp169–171(in Chinese)[盛新庆 2016电磁理论、计算、应用(北京:高等教育出版社)第169—171页]
[10]Kong J A 1986 E lectroMagnetic Wave Theory(NeWYork:Wiley-Interscience)pp381–383
[11]Ge D B 2009 E lectroMagnetic Wave Theory(Beijing:Science Press)pp334–337(in Chinese)[葛德彪 2009 电磁波理论 (北京:科学出版社)第334—337页]
[12]Zhang S J 2009 Engineering E lectroMagnetics(Beijing:Science Press)pp638–640(in Chinese)[张善杰 2009 工程电磁场 (北京:科学出版社)第638—640页]
[13]Yang R G 2008 Advanced E lectroMagnetic Theory(Beijing:Higher Education Press)pp175–177(in Chinese)[杨儒贵 2008高等电磁理论 (北京:高等教育出版社)第175—177页]
[14]Gong Z L 2010 Modern E lectroMagnetic Theory(2nd Ed.)(Beijing:Peking University P ress)pp288–291(in Chinese)[龚中麟2010近代电磁理论第2版(北京:北京大学出版社)第288—291页]
[15]Schot S H 1992 Hist.Math.19 385
[16]SomMerfeld A 1949 Partial D ifferen tia l Equations in Physics(NeWYork:AcadeMic Press)pp188–193
[17]Ji J R 2007 Advanced Optical Tutorial(Beijing:Science Press)pp166–168(in Chinese)[季家镕 2007高等光学教程 (北京:科学出版社)第166—168页]
[18]GoodMan JW1996 In troduction to Fourier Optics(2nd Ed.)(NeWYork:McG raw-Hill)pp42–44
[19]Huang K Z 2009 Tensor Analysis(2nd Ed.)(Beijing:Tsinghua University Press)pp139–149(in Chinese)[黄克智2009张量分析第2版 (北京:清华大学出版)第139—149页]
[20]Sheng X Q 2008 A Brief Treatise on CoMputational E lectroMagnetics(2nd Ed.)(Hefei:Press of University of Science and Technology of China)pp42–43(in Chinese)[盛新庆 2008计算电磁学要论第2版 (合肥:中国科学技术大学出版社)第42—43页]
[21]Tai C T 1997 Generalized Vector and Dyadic Analysis(2nd Ed.)(NeWYork:Wiley-Interscience)pp124–127
(Center for ElectroMagnetic Simu lation,Beijing Institute of Technology,Beijing 100081,China)(Received 23 February 2017;revised Manuscrip t received 3 June 2017)
PACS:42.25.Fx,24.10.Ht,92.60.TaDOI:10.7498/aps.66.164201
*Pro ject supported by the National K ey R&D PrograMof China(G rant No.2017YFB 0202500).
†Corresponding author.E-Mail:xsheng@bit.edu.cn
F laWs in classical p roo fs of vector K irchhoff integral theoreMand its neWstrict p roof∗
Huang Xiao-Wei Sheng Xin-Qing†
The vector K irchhoff integral theorem(VK I)is an iMportant formu la in electroMagnetic(EM)theory,especially it is a basis of the op tical diff raction theory.Recently,it has been found that there exist soMe flaws in the proofs presented in the literature.
There aremainly two types ofmethods to p rove the VK I.The fi rst type ofmethod is to emp loy the vector analysis to prove the VK I directly.Some flaws of this type of proof p resented in the literature have been found and pointed out in this paper.The second type ofmethod is to eMp loy the scalar K irchhoff Integral(SK I)to directly obtain the VK I.The SK Iwas fi rst derived by K irchhoff(1882).In spite of itsmathematical inconsistency and its physical deficiencies,the SK Iworks reMarkably well in the optical doMain and has been the basis ofMost of thework on diff raction.However,the proofs for SK I usually need the scalar radiation conditions.The scalar radiation condition was fi rst proposed by Sommerfeld to ensure the uniqueness of the solution of certain exterior boundary value p robleMs inMatheMaticalphysics.But whether the scalar radiation conditionswere suitab le for the EMwas not sure.In fact,for electroMagnetic field,we have another vector radiation conditions which have been verified to be adaptab le for all the radiation and scattering fields.It is diffi cult to obtain the scalar radiation conditions directly by just separating three Cartesian directions froMthe vector one,because the diff erent scalar coMponents are coup led together after the rotation and cross p roduct operation.Actually,feWstrict p roofs could be found to support the fact that EMsatisfies the scalar radiation condition.So as the supp lementary,the scalar radiation conditionsWill be derived in detailWith far-field app roximation method in this paper.
To avoid using the scalar radiation condition whichmay bring some non-rigorousness,we perforMa neWstrict p roof for the VK Iby using the vector analysis identities.
The rest of this paper is organized as folloWs.In Section 2,the diff erent proofs presented in the classical books Will be analyzed in detail.The flaws existing in these p roofs Will be pointed out.A fter that,in Section 3,based on the Stratton-Chu formula,a neWstrict proofWillbe given With using the vector identities.In Section 4,a sensitivity analysis is nuMerically perforMed to confi rMour deMonstration.Finally,the conclusions are drawn froMthe present study in Section 5.The scalar radiation conditions Will be discussed in the appendix.
vector K irchhoff integral theorem,Stratton-Chu formula,Sommerfeld radiation condition
10.7498/aps.66.164201
∗国家重点研发计划项目(批准号:2017YFB 0202500)资助的课题.
†通信作者.E-Mail:xsheng@bit.edu.cn
©2017中国物理学会C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn

