牛顿法在两类弱Hölder条件下的收敛性*
徐秀斌, 李凯富
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
牛顿法在两类弱Hölder条件下的收敛性*
徐秀斌, 李凯富
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
对于Banach空间中一般的非线性方程,在一阶导数满足L平均的仿射径向Hölder条件下,讨论了经典牛顿迭代法的局部收敛性,得到了局部收敛性条件,同时证明了该方法的R收敛阶至少为1+p.在F′满足L平均的Hölder条件下,利用递推关系,给出了牛顿法的半局部收敛性定理.
牛顿法;L平均的仿射径向Hölder条件;L平均的Hölder条件;局部收敛性;半局部收敛性
0 引 言
在工程和应用数学上有大量的问题需要求非线性方程的解,然而这类非线性方程中的大部分都没有解析解,因此需要用数值逼近的方法去求方程的近似解.通常,用迭代法得到一个收敛序列,用来逼近原方程的解.牛顿法是应用最为广泛的方法之一,众多学者对牛顿法的收敛性做了大量的工作[1-4].
设X,Y是Banach空间,Ω⊆X是开凸子集,F:Ω⊆X→Y为非线性算子,且有连续的Fréchet导数F′.求解的非线性算子方程为

(1)
用于求解的牛顿法取如下形式:
(2)
式(2)中,x0∈Ω是初始点.研究牛顿法的收敛性质,主要是研究其局部收敛性和半局部收敛性.近年来,在局部收敛性研究方面,文献[5-6]给出了比Lipschitz条件更一般、更弱的L平均的径向Lipschitz条件:
(3)
式(3)中:x*是F(x)的零点;ρ(x)=‖x-x*‖;L是取正值的非减可积函数;xτ=x*+τ(x-x*).且在条件(3)下得到了局部收敛性的最佳半径r,即对于收敛球B(x*,r)内的任意初值x0,由式(2)产生的序列都收敛到x*,若增加球半径,则球内总存在x0,使式(2)产生的序列不收敛到x*.受文献[5-6]的启发,本文引入如下的F′满足L平均的仿射径向Hölder条件:
(4)
式(4)中:ρ(x)和L由式(3)定义;p∈(0,1].在条件(4)下证明了牛顿法(2)的局部收敛性,得到了收敛阶与解的唯一性.
关于牛顿法最经典的一类半局部收敛性定理,来源于Newton-Kantorovich定理[7],这个定理建立在如下假设之上:
1)对初始近似x0∈Ω,存在Γ0= [F′(x0)]-1∈L(X,Y),‖Γ0‖≤β,且‖Γ0F(x0)‖≤η;
2)存在常数L≥0,∀x,y∈Ω,有‖F′(x)-F′(y)‖≤L‖x-y‖;

近年来,有很多文献通过改进Newton-Kantorovich定理中的F′需满足的条件,研究了牛顿法的半局部收敛性[8-10].文献[11]用更宽松的ω-条件代替Lipschitz条件.受这些研究的启发,本文引入关于L平均的Hölder条件,即下面的条件(C2).
(C1)对初始近似x0∈Ω,存在Γ0=[F′(x0)]-1∈L(X,Y),且‖Γ0‖≤β,‖Γ0F(x0)‖≤η.

其中:ρ(x,y)=‖x-y‖;L由式(3)定义.由条件(C1)和(C2),本文通过构造实递推序列得到牛顿法(2)的半局部收敛性,此时序列{xn}具有R收敛阶至少为1+p.
1 局部收敛性分析
下面研究当F′满足L平均的仿射径向Hölder条件时方法(2)的局部收敛性,并给出了相应的局部收敛性定理.为证明本文定理,先给出如下引理:
引理1 假设F在B(x*,r)内有连续的一阶导数,F′(x*)-1存在,且F′(x*)-1F′满足L平均的中心Hölder条件
(5)

定理1 假设F(x*)=0,F在B(x*,r)内有连续的导数,F′(x*)-1存在,且F′(x*)-1F′满足L平均的仿射径向Hölder条件
(6)
式(6)中:p∈(0,1];xτ=x*+τ(x-x*);ρ(x)=‖x-x*‖;L是正的非减可积函数.若r满足
(7)
则牛顿法对任意的初值x0∈B(x*,r′)都收敛,且
(8)

证明 任意选取x0∈B(x*,r′),则由r满足式(7)可推得q<1.事实上,由L的单调性知,对任意0 xn+1-x*=F′(xn)-1(F(x*)-F(xn)+F′(xn)(xn-x*))= 其中,xτ=x*+τ(xn-x*).因此,由引理1和式(6)可得 故式(8)成立,从而可以得到牛顿法(2)具有R收敛阶至少为1+p.定理1证毕. 下面证明方程(1)解的唯一性. 定理2 假设F(x*)=0,F在B(x*,r)内有连续的导数,F′(x*)-1存在,且 F′(x*)-1F′满足L平均的中心Hölder条件 (9) 式(9)中:ρ(x)=‖x-x*‖;p∈(0,1];L是正的非减可积函数.若r满足 (10) 则方程F(x)=0在B(x*,r)内有唯一解x*. 证明 任意选取x0∈B(x*,r),设F(x0)≠0,考虑如下迭代格式: (11) 则 下面用数学归纳法证明,存在q0<1,使得 (12) (13) 接下来利用递推关系式的技巧,研究当F′满足关于L平均的Hölder条件时,牛顿法(2)的半局部收敛性,同时半局部收敛性定理给出了解的存在性、唯一性及相应的解的误差界. (15) 式(15)中: (16) 易知如下引理2: 引理2 设函数f(x)和g(x)由式(16)定义,则当x∈(0,1)时,有 1)f(x)是单调递增的,且当x∈(0,1)时,f(x)>1; 2)∀γ∈(0,1),有f(γx) 为了研究序列(15)的性质,考虑辅助函数 (17) 引理3 设函数f(x)和g(x)由式(16)定义,a0∈(0,ζ),p∈(0,1],则 1)f(a0)1+pg(a0)p<1; 2)f(ai)g(ai) 3)序列{an}是严格单调递减的,且an∈(0,ζ)对所有的n≥0都成立.若a0=ζ,则an=a0<1. 证明 用数学归纳法证明1).当n=2时,由式(15)和引理3可知 引理5 若a0∈(0,ζ),x1∈Ω,在(C1)和(C2)条件下,由递推关系式(15)产生的序列{an}及式(2)产生的序列{xn}满足如下性质: 1)Γn-1=[F′(xn-1)]-1存在,且‖Γn-1‖≤f(an-2)‖Γn-2‖,n≥2; 2)‖xn-xn-1‖≤f(an-2)g(an-2)‖xn-1-xn-2‖,n≥2. 由式(2)可得, 因此, f(a0)g(a0)‖x1-x0‖<‖x1-x0‖. 从而, 所以 由算子的Banach引理知,存在算子Γn-1=[F′(xn-1)]-1,且 另外, 从而, ‖xn-xn-1‖≤‖Γn-1‖‖F(xn-1)‖≤ f(an-2)f(an-3)…f(a0)‖Γ0‖Lm‖xn-1-xn-2‖p‖xn-1-xn-2‖≤ f(an-2)f(an-3)…f(a0)‖Γ0‖Lm[f(an-3)g(an-3)…f(a0)g(a0)]p‖x1-x0‖p‖xn-1-xn-2‖≤ 由数学归纳法可知,对任意n≥1,1)和2)成立,且xn∈B(x0,R).引理5证毕. 下面给出半局部收敛性定理. (18) 则x*是式(1)的唯一解.且当a0∈(0,ζ)时,序列{xn}具有R收敛阶至少为1+p, (19) 证明 由a0∈(0,ζ)和η (20) (21) 所以xn∈B(x0,R).因为B(x0,R)⊂Ω,所以xn∈Ω,n≥0. 下证{xn}是柯西序列.由{xn}的定义知, (22) 当n→∞,对任意的m∈Z+,‖xn+m-xn‖→0,所以{xn}是柯西序列.设x*是{xn}的极限,下证x*是式(1)的解.由引理4和引理5可知, (23) 下证x*的唯一性.假设y*是F(x)=0在B(x0,R)中的另一个解,则 (24) 所以式(18)保证了‖I-Γ0T‖<1.由Banach引理知,算子T的逆存在,所以x*=y*. 本文先讨论了牛顿法的局部收敛性,得到了F′满足L平均的仿射径向Hölder条件时的收敛球半径,以及F′满足L平均的中心Hölder条件时方程具有唯一解的球半径;接着讨论了牛顿法在满足关于L平均的Hölder条件下的半局部收敛性和收敛阶.但本文未给出局部收敛性中牛顿法收敛球的最优半径和方程具有唯一解的最优半径,这是值得以后继续研究的课题. [1]Xu Xiubin,Li Chong.Convergence criterion of Newton′s method for singular systems with constant rank derivatives[J].J Math Anal Appl,2008,345(15):689-701. [2]Argyros I K.Improved estimates on majorizing sequences for the Newton-Kantorovich method[J].J Appl Math Comput,2010,32(1):1-18. [3]Ren Hongmin,Argyros I K.On convergence of the modified Newton′s method under Hölder continuous Fréchet derivative[J].Appl Math Comput,2009,217(15):440-448. [4]Argyros I K.On the convergence region of Newton′s method under Hölder continuity conditions[J].Int J Comput Math,2010,87(2):317-326. [5]Wang Xinhua.Convergence of Newton′s method and uniqueness of the solution of equations in Banach spaces[J].IMA J Numer Anal,2000, 20(1):123-134. [6]Wang Xinhua.Convergence of Newton′s method and inverse function theorem in Banach space[J].Math Comp,1999,68(225):169-186. [7]Ortega J M.The Newton-Kantorovich theorem[J].Amer Math Monthly,1968,75(6):658-660. [8]Ezquerro J A,Hernndez M A.On the domain of starting points of Newton′s method under center Lipschitz conditions[J].Mediterr J Math,2016,13(4):2287-2300. [10]Ezquerro J A,Gonzlez D,Hernndez M A.Majorizing sequences for Newton′s method from initial value problems[J].J Comput Appl Math,2012,236(9):2246-2258. [11]Ezquerro J A,Hernndez M A.On an application of Newton′s method to nonlinear operator withω-conditioned second derivative[J].BIT,2002,42(3):519-530. (责任编辑 陶立方) Convergence analysis of Newton method under two types of weak Hölder condition XU Xiubin, LI Kaifu (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China) Under the affine radius Hölder condition withLaverage for the first order Fréchet derivative, the local convergence of classical Newton method for solving nonlinear equations was studied. Some local convergence conditions were given, theR-order of convergence was proved to be at least 1+punder those conditions. Under Hölder condition withLaverage for the first order Fréchet derivative, by the technique based on recurrence relation instead of majorant principle, the semilocal convergence theorem was established. Newton method; affine radius Hölder condition withLaverage; Hölder condition withLaverage; local convergence; semilocal convergence 10.16218/j.issn.1001-5051.2017.03.001 �2017-03-11; 2017-04-15 国家自然科学基金资助项目(11671365);浙江省自然科学基金资助项目(17A010006) 徐秀斌(1962-),男,浙江兰溪人,教授,博士.研究方向:数值逼近.> O241.7 A 1001-5051(2017)03-0241-08









2 半局部收敛性分析


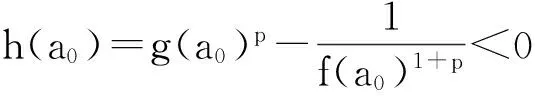




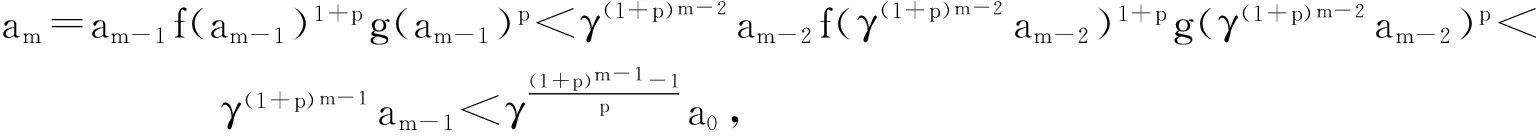



















3 结 语

