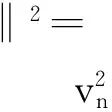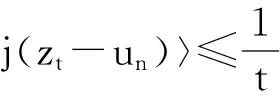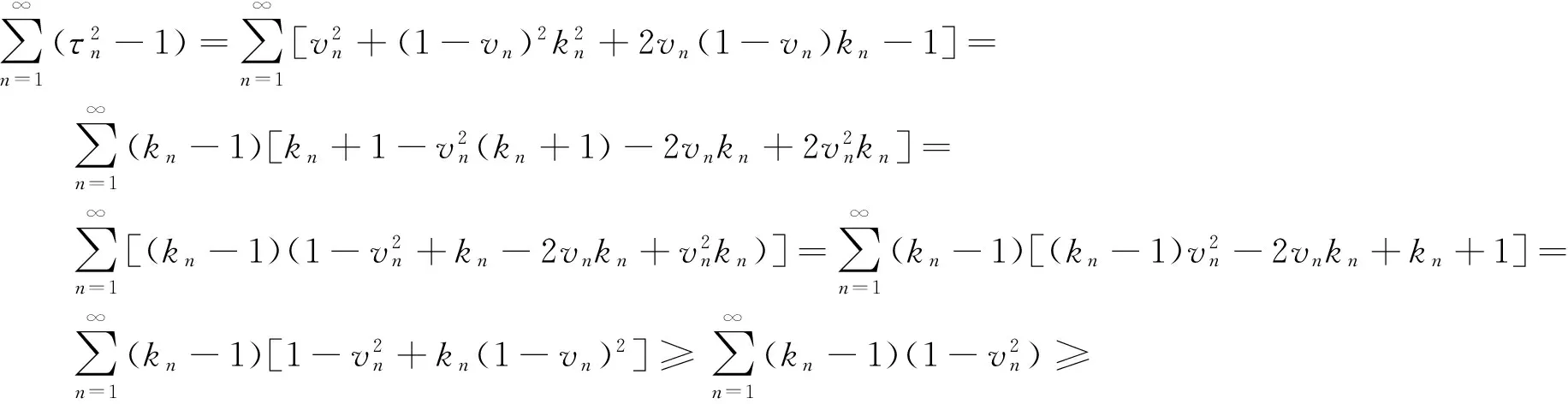广义拟变分包含解与渐近非扩张映射不动点的公共迭代算法逼近*

王元恒, 郭慧芳

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

广义拟变分包含解与渐近非扩张映射不动点的公共迭代算法逼近*

王元恒, 郭慧芳

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

在Banach空间中建立了一种新的关于求广义拟变分包含解与渐近非扩张映射不动点的公共元素的迭代逼近算法，且在一定条件下证明了该迭代序列的强收敛性.结果改进和推广了现有的一些相关结果.

广义拟变分包含;渐近非扩张映射;迭代算法;强收敛;Banach空间

0 引 言

设E是实Banach空间,E*是E的对偶空间,C是E的非空闭凸子集.假设A:C→E是单值非线性映射,B:C→2E是多值映射.广义拟变分包含问题就是:找v∈C,使得

(1)

其解集记为 (A+B)-1(0).

变分包含是变分不等式的重要推广形式之一,许多变分不等式都是它的特殊情形.例如:

1)若B=∂φ:E→2E,其中∂φ是φ的次微分,则广义拟变分包含问题(1)等价于:寻找v∈E,使得

其中,j∈J为空间E上的正规对偶映射.称此问题为混合型拟变分不等式问题.

2)若设1)中的E=E*=Rn为n维欧氏空间,φ=δC:E→[0,∞)是C的指标函数,即

则拟变分包含问题(1)等价于：寻找u∈C,使得

此问题就是经典的Hartman-Stampacchia变分不等式问题[1].自20世纪60年代该问题提出以来,由于它描述了具有广泛应用的有界边值问题的理论,立即引起了人们的极大兴趣和关注,经过众多学者[1-9]的工作,形成了“变分不等式理论”这一强有力的非线性分析工具,现在被广泛应用在偏微分方程、最优化理论、不动点理论、非线性规划、经济均衡理论、控制论、电路分析、力学、物理学、工程数学等学科领域中.

同时,许多学者把变分不等式(包含)和不动点理论、均衡问题相结合,从空间、内容、形式、映射和迭代算法等各个方面作了混合推广和应用,得到了大量成果[2-8]. 特别是文献[9],首先提出和研究了实Hilbert空间中的变分包含问题.之后,又有一些学者改进和推广了变分包含的内容与应用，得到了许多结果.例如,文献[10]研究了有限族的变分包含问题;文献[11]介绍了用迭代算法解决Banach空间中一类新的广义的非线性拟变分包含问题;文献[12]给出了变分包含解和非扩张映像不动点的公共算法;文献[13]介绍了Hilbert空间中拟变分包含和公共不动点问题的一些结论和应用;文献[14]研究了有限族变分包含解与λ-强伪压缩映射不动点的逼近问题;文献[15]研究了变分包含解和伪压缩映射不动点的新的迭代算法,构建了如下的迭代过程:

(2)

式(2)中:λ,v,t为常数;{αn},{βn}为数列;T,F,f为映射.并在一定条件下证明了序列{xn}强收敛于u=PF(I-F+f)u,其中F=Fix(T)∩(A+B)-1(0).

受上述结果启发,笔者在Banach空间中构建了广义拟变分包含解与渐近非扩张映射不动点的新的迭代逼近算法,把非扩张映射推广为渐近非扩张映射,把式(2)中的常数v推广为数列{vn},利用正规对偶映射J把Hilbert空间推广到Banach空间;并在关于迭代系数的一定条件下，证明了这些迭代逼近算法的强收敛性.本文结果在一定程度上改进和推广了现有的一些相关结果[3-6,10-15].

1 预备知识

设E是一个实Banach空间,E*是E的对偶空间,J:E→2E*是如下定义的正规对偶映像:

由Hahn-Banach延拓定理知,∀x∈E,J(x)≠Ø.当E是一个Hilbert空间时,J(x)=I(x)为恒等映射.

定义1 设C是实Banach空间E的非空有界闭凸子集,T:C→C是一映像,Fix(T)表示T在D的不动点集.

2)对任意的x,y∈C,若存在j(x-y)∈J(x-y),使得〈Tx-Ty,j(x-y)〉≥k‖x-y‖2,则称映像T为k-强增生的.

3)对任意的x,y∈C,若存在j(x-y)∈J(x-y),使得〈Tx-Ty,j(x-y)〉≥η‖Tx-Ty‖2,则称映像T为η-逆强增生的.

4)映像M:C→2E是多值的,对任意的x,y∈C,若存在j(x-y)∈J(x-y),使得〈Mx-My,j(x-y)〉≥0,则称M为增生映射,而称映射Jρ,M:E→E,Jρ,M(u)=(I+ρM)-1(u),∀u∈E为关于M的预解算子,其中ρ是任意的正数,I是恒等映射.

为了证明本文的主要结果，还需要下列重要引理.

引理1[19]对任意的ρ>0,若M是增生映射,则定义1中的Jρ,M是单值和非扩张的.

引理2[20]在实Banach空间中,Br={z∈E:‖z‖≤r},r>0,存在一个严格增的连续凸函数g:[0,2r]→R,g(0)=0,使得∀t∈[0,1],有

引理3[21]设{rn}不是无限递减的实序列,即对任意的k≥0,{rn}至少存在一个子序列{rnk},使得rnk≤rnk+1.于是,对每个n≥N,定义整数序列{τ(n)}为τ(n)=max{i≤n:rni

引理5[23]令E是一致凸且2-一致光滑的Banach空间,C是E的非空闭凸子集,QC:E→C是太阳非扩张保核映射,A:C→E是α-逆强增生算子.那么u∈C是变分不等式〈Au,j(v-u)〉≥0,∀v∈C的解,当且仅当u满足u=QC(u-λAu).

2 算 法

本节建立2个新的迭代算法,以此逼近计算广义拟变分包含解和渐近非扩张映射不动点的公共元素.

算法1 设E是一致凸且2-一致光滑的自反的Banach空间,C是E的非空有界闭凸子集,T:C→C是具有渐近系数{kn}的渐近非扩张映射.假定A:C→E是α-逆强增生映射,B是E上的增生映射,B的定义域包含在C内,且F:=Fix(T)∩(A+B)-10 ≠Ø.令Jλ,B=(I+λB)-1是B的关于λ>0的预解式,f是ρ-压缩映射.对x0∈C,∀n∈N,定义序列{xn}为

(3)

式(3)中:{αn},{vn},{βn}⊂(0,1),{kn}⊂[1,∞)是 4个序列;τn=vn+(1-vn)kn且满足

算法2 设E是一致凸且2-一致光滑的自反Banach空间,C是E的非空闭凸子集.假定T:C→C是非扩张映射,A:C→E是α-逆强增生映射,B是E上的增生映射,B的定义域包含于C内,且F:=Fix(T)∩(A+B)-1(0)≠Ø.令Jλ,B=(I+λB)-1是B的关于λ>0的预解式,f是ρ-压缩的,v∈(0,1).对x0∈C,∀n∈N,定义{xn}为

(4)

式(4)中,{αn},{βn}⊂[0,1]是2个序列,且满足:

3 主要结果

证明 取x*∈Fix(T)∩(A+B)-1(0),则x*=Tnx*=Jλ,B(I-λA)x*,从而可以得到

‖zn-x*‖2=‖Jλ,B(I-λA)x*-Jλ,B(I-λA)xn‖2≤‖xn-x*-λ(Axn-Ax*)‖2=

‖xn-x*‖2-2λ〈Axn-Ax*,j(xn-x*)〉+λ2‖Axn-Ax*‖2≤

‖xn-x*‖2-2λα‖Axn-Ax*‖2+λ2‖Axn-Ax*‖2=

‖xn-x*‖2-λ(2α-λ)‖Axn-Ax*‖2≤‖xn-x*‖2,

即

(5)

同样可得

(6)

式(6)中,τn=vn+(1-vn)kn=1+(1-vn)(kn-1).因为kn→1 (n→∞),{vn}⊂(0,1),所以可以得到τn→1 (n→∞).由式(6)可得

(7)

令un=βnf(xn)+(1-βn)yn,n≥0.因为f是ρ-压缩的,所以

‖un-x*‖=‖βnf(xn)+(1-βn)yn-x*‖=‖βn(f(xn)-x*)+(1-βn)(yn-x*)‖≤

βn(‖f(xn)-f(x*)‖+‖f(x*)-x*‖)+(1-βn)τn‖xn-x*‖≤

βnρ‖xn-x*‖+βn‖f(x*)-x*‖+(1-βn)τn‖xn-x*‖=

(βnρ+(1-βn)τn)‖xn-x*‖+βn‖f(x*)-x*‖.

(8)

由式(3)和式(8)得

‖xn+1-x*‖=‖αn(xn-x*)+(1-αn)(un-x*)‖≤αn‖xn-x*‖+(1-αn)‖un-x*‖≤

αn‖xn-x*‖+(1-αn)[(βnρ+(1-βn)τn)‖xn-x*‖+βn‖f(x*)-x*‖]=

[1-(1-αn)(1-βnρ-(1-βn)τn)]‖xn-x*‖+(1-αn)βn‖f(x*)-x*‖.

(9)

由{xn}的定义知

xn+1-xn=αnxn+(1-αn)(βnf(xn)+(1-βn)yn)-xn=(1-αn)[βnf(xn)-βnyn+yn-xn].

(10)

因此,

〈xn+1-xn,j(xn-x*)〉=(1-αn)〈[βnf(xn)-βnyn+yn-xn],j(xn-x*)〉=

(1-αn)βn〈f(xn),j(xn-x*)〉-(1-αn)βn〈yn,j(xn-x*)〉+(1-αn)〈yn-xn,j(xn-x*)〉.

(11)

因‖xn+1-x*‖2=‖(xn+1-xn)+(xn-x*)‖2=‖xn+1-xn‖2+‖xn-x*‖2+2〈xn+1-xn,j(xn-x*)〉,故

同理可得

由式(11)、式(5)和式(7)得

‖xn+1-x*‖2-‖xn+1-xn‖2-‖xn-x*‖2=

2(1-αn)βn〈f(xn),j(xn-x*)〉-2(1-αn)βn〈yn,j(xn-x*)〉+

(1-αn)[‖yn-x*‖2-‖yn-xn‖2-‖xn-x*‖2]≤

因此,

2(1-αn)βn〈f(xn),j(xn-x*)〉-2(1-αn)βn〈yn,j(xn-x*)〉-(1-αn)‖yn-xn‖2.

(12)

由式(10)可得

(13)

结合式(12)和式(13),有

2(1-αn)βn〈f(xn),j(xn-x*)〉-2(1-αn)βn〈yn,j(xn-x*)〉-

2βn‖f(xn)-yn‖‖yn-xn‖]=

(14)

因此,

(15)

由式(15)可得

(1-αn)αn‖yn-xn‖2≤

(16)

现在分成2种情况进行证明.

(17)

结合式(13)即可推出

(18)

注意到

(19)

所以

因〈(I-f)(x-y),j(x-y)〉=〈x-y,j(x-y)〉-〈f(x)-f(y),j(x-y)〉≥‖x-y‖2-ρ‖x-y‖2=(1-ρ)‖x-y‖2,故I-f是(1-ρ)-强增生算子.于是,由引理5知,变分不等式〈(I-f)y,j(x-y)〉≥0,∀x∈F有解x*的充要条件是x*=QFf(x*).

接下来证明

现定义一个映射W:E→E,对每个y∈E,W(y)=vy+(1-v)Tn(y).易知W是非扩张映射且Fix(T)=Fix(W),序列 {W(un)}收敛于E中的不动点,于是

(20)

定义映射Z:z→tf(x*)+(1-t)W(z),t∈(0,1),则Z是压缩映射.令zt是映射Z的一个不动点,即zt=tf(x*)+(1-t)W(zt),于是

‖zt-un‖=‖tf(x*)+(1-t)W(zt)-un‖=‖t(f(x*)-un)+(1-t)(W(zt)-un)‖.

对∀t∈(0,1),有

‖zt-un‖2=t〈f(x*)-un,j(zt-un)〉+(1-t)〈W(zt)-un,j(zt-un)〉=

t〈f(x*)-zt,j(zt-un)〉+t〈zt-un,j(zt-un)〉+(1-t)〈W(zt)-W(un),j(zt-un)〉+

(1-t)〈W(un)-un,j(zt-un)〉≤

t〈f(x*)-zt,j(zt-un)〉+t‖zt-un‖2+(1-t)‖zt-un‖2+(1-t)‖W(un)-un‖‖zt-un‖=

t〈f(x*)-zt,j(zt-un)〉+‖zt-un‖2+(1-t)‖W(un)-un‖‖zt-un‖≤

t〈f(x*)-zt,j(zt-un)〉+‖zt-un‖2+‖W(un)-un‖‖zt-un‖.

(21)

|〈f(x*)-x*,j(un-x*)〉-〈zt-f(x*),j(zt-un)〉|≤

|〈f(x*)-x*,j(un-x*)〉-〈f(x*)-x*,j(un-zt)〉|+

|〈f(x*)-x*,j(un-zt)〉-〈zt-f(x*),j(zt-un)〉|=

|〈f(x*)-x*,j(un-x*)-j(un-zt)〉|+|〈x*-zt,j(zt-un)〉|≤

‖f(x*)-x*‖‖j(un-x*)-j(un-zt)‖+‖x*-zt‖‖zt-un‖.

(22)

令t→0,式(22)右端趋于0.因此,∀ε>0,∃δ>0,使得对∀t∈(0,δ),下面的不等式成立:

因此,

结合式(21),有

(23)

注意到

得

‖un-x*‖2=〈βn(f(xn)-x*)+(1-βn)(yn-x*),j(un-x*)〉=

βn〈f(xn)-f(x*),j(un-x*)〉+βn〈f(x*)-x*,j(un-x*)〉+(1-βn)〈yn-x*,j(un-x*)〉≤

βn〈f(x*)-x*,j(un-x*)〉.

因此,

应用引理2有

‖xn+1-x*‖2=‖αn(xn-x*)+(1-αn)(un-x*)‖2≤

αn‖xn-x*‖2+(1-αn)‖un-x*‖2=

(24)

于是,相应于引理4,可以分别令

(25)

因为τn=vn+(1-vn)kn,所以

(26)

故an→0,即xn→x*(n→∞).

2)假设存在一个整数n0,使得‖xn0-x*‖≤‖xn0+1-x*‖.令ψn={‖xn-x*‖},可以推出ψn0≤ψn0+1.定义整数序列{π(n)}为

显然,π(n)是个非减序列,且满足

由式(16)可得

(1-απ(n))απ(n)‖yπ(n)-xπ(n)‖2≤

因此,

(27)

因为ψπ(n)≤ψπ(n)+1,所以由式(27)取上极限得

于是必有

(28)

应用引理3得0≤ψn≤max{ψπ(n),ψπ(n)+1},再结合式(28)可得ψn→0,即xn→x*.定理1证毕.

证明 在定理1及其证明过程中,对∀n∈N,取kn=1,vn=v,完全类同于定理1中的方法(可以省略许多过程和技巧),可以证明得到此结论.

注2 1)定理2实际上给出了完全不同于文献[15]的另一种证明方法,其结果也由Hilbert空间推广到Banach空间;2)定理1给出了Banach空间中对于具有系数{kn}(kn→1)的渐近非扩张映射T的不动点与广义变分包含0∈Av+Bv解的公共元素,分别取映射T,A,B为特殊映射时即为原来一些已知结果.例如:映射T可以分别取渐近非扩张映射、非扩张映射、恒等映射;映射A可以分别取逆强增生映射、0映射、恒等映射;映射B可以分别取增生映射、0映射、某个泛函φ的次微分∂φ、某个凸集C的指标函数次微分;空间可以分别取Banach空间、Hilbert空间和Euclid空间等.可以得到几十种不同的关于变分包含、变分不等式解与映射零点、不动点的结果.因此,本文结果在一定情况下推广和改进了许多已有的结果[3-6,10-15].

[1]HartmanP,StampacchiaG.Onsomenonlinearellipticdifferentialfunctionalequations[J].ActaMath,1966,115(1):271-310.

[2]LionsJL,StampacchiaG.Variationalinequalities[J].CommuPureApplMath,1967,20(2):493-519.

[3]MuhammadAN.Somedevelopmentsingeneralvariationalinequalities[J].ApplMathCompu,2004,152(1):15-35.

[4]金坚帅,倪仁兴.Banach空间中一族依中间意义渐近拟非扩张映射和均衡问题的强收敛性定理[J].浙江师范大学学报:自然科学版,2015,38(2):163-171.

[5]石慧敏,王元恒.渐近伪压缩映像不动点的三步带误差修正迭代逼近[J].系统科学与数学,2014,34(1):119-128.

[6]李柳红,王元恒.渐近非扩张型映像不动点的粘性逼近法[J].浙江师范大学学报:自然科学版,2015,38(1):41-46.

[7]王元恒,谢飞.Banach空间中分层不动点的黏性连续型广义逼近格式的收敛性[J].浙江师范大学学报:自然科学版,2016,39(3):246-252.

[8]SongYL,CengLC.StronglyconvergenceofageneraliterativealgorithmforafinitefamilyofaccretiveoperatorsinBanachspaces[J].FixedPointTheoryAppl,2015,10(1):1-13.

[9]HassouniA,MoudafiA.Aperturbedalgorithmforvariationalinclusions[J].JMathAnalAppl,1994,185(3):706-712.

[10]王元恒.Banach空间中有限簇广义集值拟变分包含[J].浙江师范大学学报:自然科学版,2004,27(2):109-114.

[11]Ding X P,Feng H R.Algorithm for solving a new class of generalized nonlinear implict quasi-variational inclusion in Banach space[J].Appl Math Compu,2009,208(2):547-555.

[12]Chang S S,Lee J H,Chan C K.Algorithms of common solution for quasi-variational inclusion and fixed point problems[J].Appl Math Mech-Engl(Ed),2008,29(5):571-581.

[13]Hao Y.On variational inclusion and common fixed point problems in Hilbert spaces with applications[J].Appl Math Compu,2010,217(7):3000-3010.

[14]Zhu J H.Approximation of solutions to finite family of varional inclusion and the set of common fixed point for finite family ofλ-strict pseudo-contraction mapping in Banach spaces[J].Math Appl,2013,43(19):207-217.

[15]Yao Y H,Agarwal R P,Liou Y C.Iterative algorithms for quasi-variational inclusions and fixed point problems of pseudocontractions[J].Fixed Point Theory Appl,2014,82(1):1-14.

[16]Li J L.The generalized projection operator on reflexive Banach spaces and its applications[J].J Math Anal Appl,2015,306(1):55-71.

[17]Kamimura S,Takahashi W.Strong convergence of a proximal-type algorithm in a Banach space[J].SIAM J Optim,2002,13(3):938-945.

[18]王元恒,曾六川.Banach空间中广义投影变形迭代法的收敛性[J].数学年刊,2009,30A(1):55-62.

[19]Chang S S,Cho Y J,Zhou H Y.Iterative methods for nonlinear operator equations in Banach spaces[M].New York:Nevs Sci Pub Inc,2002:47-68.

[20]Xu H K.Inequalities in Banach spaces with applications[J].Nonlinear Anal,1991,16(12):1127-1138.

[21]Mainge P E.Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces[J].J Math Anal Appl,2007,325(5):469-479.

[22]Xu H K.Iterative algorithms for nonlinear operators[J].J Lond Math Soc,2002,2(1):1-17.

[23]Aoyama K,Iiduka H,Takashi W.Weak convergence of an iterative sequence for accretive operators in Banach spaces[J].Fixed Point Theory Appl,2006,35(2):378-390.

(责任编辑 陶立方)

A new iterative algorithm for the common elements of solutions of generalized quasi-variational inclusions and fixed points of asymptotical nonexpansive mappings

WANG Yuanheng, GUO Huifang

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

A new iterative algorithm was established to approximate the common elements of solutions of generalized quasi-variational inclusions and fixed points of asymptotical nonexpansive mappings. Under certain conditions, some strong convergence theorems were obtained for the iterative sequence in Banach spaces. The results extended and improved some corresponding results reported by other authors.

generalized quasi-variational inclusion; asymptotical nonexpansive mapping; iterative algorithm; strong convergence; Banach space

10.16218/j.issn.1001-5051.2017.03.002

�2016-12-09；

2017-01-05

国家自然科学基金资助项目(11671365)；浙江省自然科学基金资助项目(LY14A010011)

王元恒(1961-),男，河南南阳人，教授.研究方向：非线性泛函分析.>

O177.91

A

1001-5051(2017)03-0249-09