增进学生理解 弘扬主体精神——数学教学设计从逻辑分析转向心理分析的视点

淮北师范大学数学科学学院 张 昆 (邮编:235000)

聚焦新课程

增进学生理解 弘扬主体精神
——数学教学设计从逻辑分析转向心理分析的视点

淮北师范大学数学科学学院 张 昆 (邮编:235000)

数学教学所要传授的知识相对固定(其最低限度已经写入课程标准)．但是,通过何种方式来传授这种已经设定了的知识,却随着教师的教学理念不同,预设的教学目标不同,持有的教学观念不同,获得的教学经验不同,理解特定数学知识性质不同,揣摩发生特定知识的学生认知方式不同,估计发生知识时学生现场心理活动意向不同,存在多种选择余地．不同的教学设计对发挥数学知识的教育价值,促进学生素质发展的结果大相径庭、迥然有别．本文主要探讨数学教学设计时,尊重学生的想法,即提高教学的有效性．我们先从历史上非常有名的一个知识点的教学设计的课例说起．

1 从马克斯·韦特海麦的一个教学设计课例说起

早期的格式塔心理学家把他们对知觉过程的分析扩展到思维的发展,并且在某些重要的方面,他们预见了并奠定了直到现在的对于认识发展的系统阐述的基础．格式塔心理学发展史中的许多有名人物虽然主要地谈论到知觉,但也确实涉及到了认识,其中,考夫卡在《心理的发展》一书中提供了一个详细的理论分析,试图说明儿童的认识发展;苛勒运用这些原则去解释类人猿解决问题的行为;马克斯·韦特海麦在他的《创造性思维》中对课堂教学的有效和无效以及按照知觉的完形原则学习进行了详尽的分析,这些认识与原理对数学教学的有效性标准提供了有意义的参考．这里引入韦特海麦提供的一个课题(平行四边形面积)教学活动的课例:求平行四边形的面积公式．

师:上一堂课我们学习了如何求一个长方形的面积,你们都懂了吗?

生1:懂了．一个长方形的面积等于两边的乘积．

师:(板书平行四边形图形,图1),这个四边形叫平行四边形,一个平行四边形是一个四边形的平面,它的对边相等且平行(教师在图1的四个角上写上a、b、c、d)．

师:我从左上角画一条垂直线,从右上角画一条垂直线,我把底边向右延长,我把这两个新点表上e和f(图2)．

接着,教师着手证明定理——平行四边形的面积等于底乘高的积．证明的活动过程是通过确立某些角和边的等量关系和一对三角形的全等来进行的．到此,教师提出了许多问题,都是要求平行四边形的面积,但它们的大小、边和角不相同,学生都能够顺利地完成．在结束这节课以前,教师指定了十多个这类问题作为家庭作业．如此看来,这节课应该是比较成功的了．

不过,一天后,这个班的下一节课,我又去了．课开始时,教师叫一个学生来证明平行四边形的面积．学生正确地回答了……一个书面的作业,得到了很好的效果．此时,我问教师是不是让我在这个班提出一个问题．这位教师答应了,显然,他以他的课为荣．

我在黑板上画了一个图3,让学生求它的面积．

生2:老师,我们还没有学习过这个．

另外的学生忙起来了．他们把图形抄在纸上,像被教的那样画辅助线,从两个上角向下画垂直线和延长底边(图4)．然后,他们看起来迷惑、发窘．经过一段时间思考以后,有些同学看起来是完全不愉快的;他们自信地在他们的图下写着“面积等于底乘高”——一个正确的设想,但也许完全是盲目的．当问他们能否证明在这种情况下它也是正确的时,他们露出了迷惑．另一些同学则情况完全不同,他们是愉快的,他们在笑．他们把他们的纸转动了一个角度……[1]．

韦特海麦所出示的图3当然就是这个任课教师所出示的图1,只不过将其进行了一些转动而已．显然,经过任课教师所教学的图1,对于许多学生来说,他们的收获只是掌握了一个狭隘的练习,而没有对知识形成实质性的理解,韦特海麦所设定的主旨强调的是,以确定增进理解的,并且依据对所包含的过程的心理分析而不是逻辑分析的教学方法来教解决问题的技巧．作为数学教师必须清醒地认识到,这种从逻辑分析向心理分析转化与过渡的技巧必须作为数学教师教学设计的一项主导性目标,只有心理分析的数学教学设计才能实现数学教学活动的有效性．在教师的努力下,这项目标是可以实现的．

2 例示数学教学设计从逻辑分析转向心理分析的实现

由上述的材料可以发现,从“逻辑分析”方式转化为“心理分析”方式的数学教学设计就是教师追求数学教学设计的一项非常有价值的教学技艺．因此,为了研究数学教学设计的有效性,以求获得从“逻辑分析”型的数学教学设计转化为“心理分析”型数学教学设计的具体途径,它的一般环节与关键环节,它的具体步骤,启发一般教师可以认识到它的本质,并且萌生相应的数学教学观念,形成相应的数学教学设计的技艺,从而提高数学教学设计的有效性,最大程度地发挥数学课程资源的教育价值,实现数学新课程所拟定的数学教学目标．对于韦特海麦这个课例,我们需要对其进行进一步解释,从中提炼出相关的要素,以使我们数学教学可以得到更为直接的启示．

众所周知,对于受教育者而言,相对来说问题所提供的信息往往显得杂乱无章,不是轻而易举就能理出头绪的．于是,要达到真正地解决问题,就必须经由意识机能的过滤、比较、辨别,从中选择出一项,或几项的关联作为支点信息,并且依据这一支点信息,调用附着在观念上的存储在记忆库中众多知识框架中大致地选择出某一“知识框架”作套用支点式信息的“凝聚核”,将其他诸多信息吸附到这个“凝聚核”的周围,意识机能再对其进行调整与排列等运作,使外在于主体的信息构成一种不稳定的结构轮廓．意识机能又通过自己的监控系统,对由于自己的工作所选择出来的结构轮廓进行评价、判断,最终将外在问题提供的支点信息生成的结构轮廓,与主体所选择出作为“凝聚核”的记忆库知识框架两者之间的相关元素进行对比、比较,试图匹配(如图5所示)．[2]

由此可知,数学知识的重要性在于它提供了解决问题的框架——组织外在信息的“凝聚核”——解决问题的工具,这个框架图也可以对数学发生数学知识的实质性理解一种解释,学生只有清醒地意识到是由自己已经掌握的知识套用了外在数学化信息的过程,此时,才真正地对知识产生了理解．但是,我们知道,工具是客观的、死的、物质性的材料,它不能自行地直接作用于问题．这些可套用外在信息的知识框架的“凝聚核”是人的意识机能的产物,也就是说,在解决面临的数学问题时,意识机能始终处于激活的状态,具有能动性的一面．它不断地对已经具有的工具进行组合、调整与重组,使之变成适应性更广泛,使用更方便,或者是直接创造出全新的工具．例如,伽罗瓦引进了“置换群(加罗瓦群)”这一工具彻底解决了高次(五次或五次以上)方程根式解不存在的论断,这完全是意识机能的创造性发挥的产物,并不是伽罗瓦对前人的所获得的数学知识的累加而自然产生了这一论断．

我们不去讨论是我们遗传基因提供了先天的知识框架(“凝聚核”)呢?还是感官的通道对外在的知觉的不断积累,经由意识机能长期酝酿而得到了这一框架呢?重要的是,在数学教学设计中,当学生面临数学问题时,如果他找不到现成的、可套用外在信息的知识框架,那么,是教师..将这种作为“凝聚核”的知识框架直接提供给学生呢?还是让学生从自己意识机能中创造性地构建出知识框架,以此来套用问题提供的信息,从而使那些问题所设定的分散的信息构成相对有序的结构轮廓呢?如何回答这一问题,对能否发挥利用数学资源的教育价值,实现数学教育高层次目标影响巨大且至关重要．

“逻辑分析”型方式的数学教学设计,更多地只是将这种封装外在信息的知识框架的“凝聚核”直接地交于学生,学生不理解为什么会发现这个“凝聚核”;而“心理分析”型方式的数学教学设计,更多地是启发学生自己构建这种“凝聚核”,从而真正通过教学活动过程,促进学生对经由学习而发生的数学知识的实质性地理解．因此,在教学设计时,我们教师要作出最大努力,力求将“逻辑分析”型方式的数学教学设计转化为“心理分析”型的数学教学设计．我们再看两个具体的数学教学设计的课例．

课例1数轴定义:规定原点、正方向与单位长度的直线叫数轴．

师:有理数组成:负有理数、零、正有理数(板书)．

师;今天,可以用一直线上的点表示有理数吗?

生1:负数、正数都无限多,零只有一个,首先试试在MN上任取一点O,规定用它表示零(如图6)．

师:如此,点O将直线MN分成三部分,自身表示有理数0,称点O为“原点”．于是,负、正数该由射线OM,或射线ON(除端点O)上的点来表示．究竟哪一条射线上的点表示负数,哪一条射线上的点表示正数呢?(学生想出许多区分方案)

师:这些方案中,那种更简单、更实用呢?

生:用箭头!

师:在图6的直线MN上画一个箭头．规定用具有箭头的射线上的点表示正数,反之,表示负数．称箭头为“正方向”(如图7)．

师:在图7中表示有理数＋2?(两个同学选择不同的点A和点B,都声称要表示＋2．如图8)

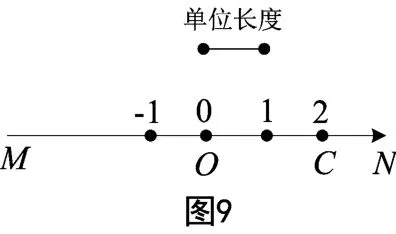
师:哪一个才是真正表示＋2的点呢?(学生决定用一把“尺子”来裁决,以原点O为起点,在具有正方向的那条射线上次第量两尺,规定“尺子”落脚的终点C为表示＋2的点．如图9)

师:“尺子”是一个度量长度的“单位”,称之为“单位长度”．

师(板书):规定了原点、正方向和单位长度的直线叫数轴．

数学教科书是采用向教师提供了运用“温度计”这种实物类比的手段促成学生发现数轴定义的,温度计中表示零度的点就是数轴的“原点”,零上的温度就是数轴上表示正有理数的那段区域,零下的温度就是数轴上表示负有理数的那段区域．许多教师基本上沿用教科书的手段,其实,这种教学途径就是沿着“逻辑分析”方式而不是“心理分析”方式进行教学设计的．当笔者向学习过了数轴定义的学生提问,“数轴定义中的‘原点’有什么作用时”,九成以上学生都不能很好地回答这个问题．这就说明教科书所提供的这种教学途径存在较大缺陷．我们给出的教学设计就是依据学生的“心理分析”过程展开,极大地增进了课堂教学的有效性．

课例2已知:如图10,在 △ABC 中,∠ADC＝∠BAC．求 证:∠CAD ＝∠CBA．[3]

师:请用不同标识在图

10中标示出所求结论与已知条件中各存在的一对相等角．

生1:在图10中,已知条件∠ADC＝∠BAC中的∠BAC被AD分割开来,图形的覆盖影响了探索问题的思路．因此,我想应该首先解决覆盖问题……

师:这是一个好建议!大家不妨可以动手试一试．

学生操作图形活动的关键环节实录:首先把图10中的△ADC平移出来,得到了图11与图13,其次,根据已知条件∠ADC＝∠BAC①和要证明的结论∠CAD＝∠CBA②,把图11变换换成图12的位置形态．到此,学生成功地运用标识标示出了图10中的两对相等角,即①,②两个等式,并且将图形转化利于进一步发现某些条件的状态．

师:大家做得非常好!现在请对比图12与图13,你有新发现吗?

生2:比较图12与图13中的这两个三角形之间角的关系可得(笔者精心设计板书):

已知条件是∠ADC＝∠BAC ①

所求结论是∠CAD＝∠CBA ②

还有公共角∠ACD＝∠BCA ③

师:对照图12与图13提供的信息,那么①②③意味着什么?

生3:在这三个等式中,①和③成立,②是求证的结论,应该成立．可是……

师:怎么办?

生:……

师:如果从整体上把握与体察,在①②③这三个角相等的等式中,这些角具有什么样的特征?它对我们有什么启发?

生4:应用“三角形的内角和等于180°”……

师:生3同学提出了一种很好的想法．如何应用“三角形的内角和等于180°”呢?

生5:①②③三个等式的左边的三个角是△DAC的三个内角,右边的三个角是△ABC的三个内角．于是,我们把这三个角的等式左、右两边分别相加就得到了这两个三角形各自的内角和,都等于180°,即

师:如何应用④⑤两个等式?

生6:两个等式左边也相等(都等于180°),即∠DAC＋∠ADC＋∠DCA＝∠ABC＋∠BAC＋∠ACB⑥．将⑥的左、右两边分别对应地减去①与③的左、右两边,就可得到②成立[4]．

这道题的教学设计活动,过去采用了∠BAC＝∠BAD＋∠CAD⑦,∠ADC＝∠BAD＋∠CBA⑧．比较⑦⑧,由于∠ADC＝∠BAC,∠BAD是公共角,故知∠CAD＝∠CBA．这就是典型“逻辑分析”方式教学设计,当在教学实践中认识到,这种教学在很大程度上掩盖了学生思维活动过程,逼着学生采用记忆的手段来记住问题的解答方法,这种教学手段是摧毁学生自信心与探究热情的利器,我们想想大多数学生学习平面几何时的那种身陷重围的痛楚、举步维艰的困惑、欲行又止的难局,就会深切地感受到我们的平面几何推理论证教学的失败其实就隐藏我们如此的“逻辑分析”方式的教学活动中．这就逼着我们教师一定要从这种“逻辑分析”方式教学设计转化为“心理分析”方式教学设计．

3 简要结语

数学的“逻辑分析”方式的过程要求褪尽铅华,洗去尘梓,纯而又纯,超凡脱俗,以至于简练到一尘不染;而“心理分析”方式的过程要求出自心意,平淡无奇,自然流畅,浑然天成,以至于趋近于无浮躁痕迹．在数学教学设计时,教师在教学设计时要悉心地分析所要教学的数学知识,分析学生发生具体数学知识时心理活动的绕不过去的环节,在掌握这两者的基础上,进行教学法的加工．其中要特别注意的是;以“逻辑分析”方式为线索,以“心理分析”方式为目标,整合这两者的优势,是发挥数学课程资源的教育价值,实现有效教学目标的基本保证．对此,我们一线数学教师应该思之再思,慎之又慎!

1 [美]克雷奇,克拉奇菲尔德,利维森,等．心理学纲要(上册)[M]．周先庚,林传鼎,张述祖,等译．北京:文化教育出版社,1980:141-142

2 张昆,曹一鸣．完善数学教师教学行为的实现途径[J]．数学教育学报,2015,24(1):33-37

3 马复．义务教育教科书·数学·七年级上[M]．北京:北京师范大学出版社,2013:121

4 张昆．整合数学教学设计的取向——基于知识发生的逻辑取向与心理取向研究[J]．中国教育学刊,2011(6):52-55

2017-07-20)