A method of determining effective elastic properties of honeycomb cores based on equal strain energy

Qiu Cheng,Guan Zhidong,Jiang Siyuan,Li Zengshan

School of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

A method of determining effective elastic properties of honeycomb cores based on equal strain energy

Qiu Cheng,Guan Zhidong*,Jiang Siyuan,Li Zengshan

School of Aeronautic Science and Engineering,Beihang University,Beijing 100083,China

Elastic properties;Homogenization;Honeycomb;Strain energy;Unit cells

A computational homogenization technique(CHT)based on the finite element method(FEM)is discussed to predict the effective elastic properties of honeycomb structures.The need of periodic boundary conditions(BCs)is revealed through the analysis for in-plane and out-of-plane shear moduli of models with different cell numbers.After applying periodic BCs on the representative volume element(RVE),comparison between the volume-average stress method and the boundary stress method is performed,and a new method based on the equality of strain energy to obtain all non-zero components of the stiffness tensor is proposed.Results of finite element(FE)analysis show that the volume-average stress and the boundary stress keep a consistency over different cell geometries and forms.The strain energy method obtains values that differ from those of the volume-average method for non-diagonal terms in the stiffness matrix.Analysis has been done on numerical results for thin-wall honeycombs and different geometries of angles between oblique and vertical walls.The inaccuracy of the volume-average method in terms of the strain energy is shown by numerical benchmarks.

1.Introduction

For the past several decades,sandwich plates with a honeycomb core have been widely used in the field of aviation.In understanding the behavior of sandwich structures under different types of load,the honeycomb core is often regarded as homogeneous solid with orthotropic elastic properties.1As a result,research on the effective elastic properties of the honeycomb core is of great essence for the calculation and design of honeycomb sandwich structures.

A computational homogenization technique(CHT)has been found to be a powerful method to predict the effective properties of structures with periodic media.In order to obtain the effective stiffness tensor,which relates to the equivalent strain and stress,this process is divided into solving six elementary boundary value problems,which refer to uniaxial tensile and shear in three directions.2–5The equivalent strain is determined after applying the unit displacement boundary conditions(BCs)on the representative volume element(RVE)cellcorresponding to one of the six elementary problems.Different methods have been used when dealing with the equivalent stress.Volume-average stress is often used to determine effective properties in the literature.2–6Catapano and Montemurro2investigated the elastic behavior of a honeycomb with doublethickness vertical walls over a wide range of relative densities and cellgeometries.Thestrain-energy based numerical homogenization technique was also used by Catapano and Jumel3in determining the elastic properties of particulatepolymer composites.Montemurro et al.4performed an optimization procedure at both meso and macro scales to obtain a true global optimum configuration of sandwich panels by using the NURBS curves to describe the shape of the unit cell.Malek and Gibson5got numerical results of a thick-wall honeycomb closer to their analytical solutions by considering nodes at the intersections of vertical and inclined walls.Shi and Tong6focused on the transverse shear stiffness of honeycomb cores by the two-scale method of homogenization for periodic media.Many researchers also seek the stress on the boundary of the RVE cell.Li et al.7used the sum of the node force on the boundary of the RVE cell to obtain the equivalent stress.Papka and Kyriakides8set plates on the top and bottom of the RVE cell to exert BCs.However,regarding honeycomb structures as a combination of cell walls and air,the stress variations on the boundary cause the boundary stress inaccurate to calculate effective properties.Some divergence still exists in numerical results of regular hexagonal honeycomb structures with analytical solutions,especially for the in-plane and outof-plane shear moduli.From the definitions of effective elastic properties expressed by Yu and Tang,9the equivalent stress is required to make sure that the RVE cell and the corresponding unit volume of the homogeneous solid undergo the same strain energy.Hence,the whole honeycomb structure containing a finite number of RVE cells have the same strain energy as that of the whole volume of the homogeneous solid.The mathematical homogenization theory(MHT)has proven that the strain energy in the RVE can be determined by the volumeaverage stress and strain.10However,it is not always suitable for the calculation of the volume-average method in the CHT.The volume-average method cannot get all precise values in the stiffness matrix,and it is found to get larger strain energy than that obtained from direct analysis in twodimensional porous composites by Hollister and Kikuchi.11Therefore,we focus on the total strain energy of the RVE cell and propose a new method to determine all the components of the stiffness tensor more accurately in terms of the strain energy.

In Section 2,the differences between the proposed energy method and previous methods are analyzed.A process to obtain 9 components of the effective stiffness tensor based on the energy method is introduced.Then,finite element(FE)models are discussed in Section 3.Convergence analysis has been done over material properties,mesh sizes,and BCs applied on the whole model.In addition,two models are proposed to acquire in-plane and out-of-plane shear moduli according to the different deformations of a single RVE cell and a finite number of RVE cells under the same loading.After establishing appropriate models for honeycomb structures,numerical results over a range of cell geometries are compared to analytical solutions in literature in the next section.Finally,Section 5 ends the paper with some conclusions.

2.Prediction method

2.1.Computational homogeneous technique

Previous experimental data and theory have proven that a honeycomb core can be classified as an orthotropic material.12Under this assumption,a honeycomb core conforms to generalized Hook’s law13as

whereu,v,andwrepresent the displacements in thex,y,andzdirections.

To determine the effective stiffness matrix of the RVE cell,six elementary BCs are applied on the RVE cell,which refer to three uniaxial extensions and three shear deformations.For each load case,only one component of the strain tensor is not zero.Then the relative stiffness component is determined by the equivalent stress.TakeC11for example,

After obtaining all the 9 independent components in the stiffness matrix,engineering constants can be derived from the compliance matrix which is the inverse of the stiffness matrix.

2.2.Energy method

Assuming that an elementary shear boundary displacement is

applied on the RVE cell(ckl–0),Eq.(4)is tenable since the boundary of the RVE cell has an identical displacement.

whereVrepresents the total volume of the RVE and subscript‘kl” stands for the certain BC.

The strain energy of the RVE cell under certain loading can be determined by the FE result as

To guarantee the RVE cell and the corresponding volume of the homogeneous material having the same strain energy,the equivalent stress in this method is

Hence,the effective modulus through this energy method is

From Eq.(1),

Adding Eqs.(10)and(11),and considering the symmetry of the stiffness matrix,

C13andC23can also be acquired by exerting similar BCs on the RVE cell.With the diagonal components obtained by the six elementary load cases,the entire stiffness matrix is determined and 9 engineering constants are then calculated from the compliance matrix.

2.3.Comparative study

As mentioned in Section 1,different methods have been applied to determine the equivalent stress.In this section,a comparative study is done among the volume-average method,the boundary method,and the energy method.

(1)Volume-average method

The equivalent stress in this method is calculated as follows:

where rklis the corresponding stress component in the stress field obtained from the FE analysis.The related shear modulus can be written as

(2)Boundary method

The equivalent stress is obtained by summing up node forces on the boundary as

whereFklis the corresponding node force on the boundary of the RVE cell andS0means the area of the section on which the displacement is applied.

Thus,the effective shear modulus is determined by

(3)Energy method

The effective property obtained by the energy method is shown in Eq.(7).

We review Eqs.(14)and(16)to compare the volumeaverage method and the boundary method.Without loss of generality,the volume-average stress in the RVE cell14is

wherei;j;k2 f1;2;3g.

Eq.(17)shows that the average stress depends uniquely on the surface loading.Here,a further proof is given to show that the average stress only relates to the average stress on the surface where the unit displacement is applied.

For a rectangular RVE cell,as shown in Fig.1,the six boundary surfaces are namedAtoFrespectively.

Fig.1 A rectangular RVE.

Consider the six elementary displacement BCs:

In this periodic media,for the two points having the same local load on SurfacesEandF,

As a result of the symmetry of both the honeycomb RVE and the applied BCs,the stress also distributes symmetrically,i.e.,

Considering the correspondence between SurfacesEandFin the periodicity of the RVE,Eq.(18)can be written as

Then under this BC,the volume-average stress can be determined from Eqs.(17)and(21)as

In this periodic media,for the two points having the same local load on SurfacesEandF,

As a result of the symmetry of both the honeycomb RVE and the applied BCs,the stress also distributes symmetrically,i.e.,

Considering the correspondence between SurfacesEandFin the periodicity of the RVE,Eq.(18)can be written as

最后，加强部门间沟通协调。科研项目实施单位要统筹协调好各部门，成立由项目管理部门、财务部门、项目实施部门共同参与的绩效评价工作小组，明确工作职责，多效并举，共同促进绩效评价工作规范有序进行。

Then under this BC,the volume-average stress can be determined from Eqs.(17)and(25)as

The above analysis shows that under both the tensions and shear deformations,the volume-average stress only depends on the average stress on the surface where the unit displacement is applied.Eqs.(22)and(26)show an equality of the volumeaverage stress and the boundary stress,which will be discussed later in Section 4.

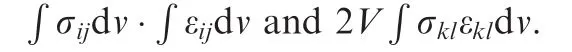
Without loss of generality,for the energy method,

Eq.(27)indicates an equality between the volume-average method and the energy method when calculating the components in the stiffness matrix.However,as mentioned in Section 2.2 for the operating process of the energy method,the equilibrium shown in Eq.(27)only exists for the diagonal elements in the stiffness matrix,because non-diagonal components can’t be calculated directly by Eq.(7).In other words,the volume-average method in the calculation of the equivalent stress is only acceptable for diagonal elements likeC11,C22,and so on,while divergence exists at non-diagonal elements.

Taking the calculation ofC12for example,in the volumeaverage method,C12is calculated as

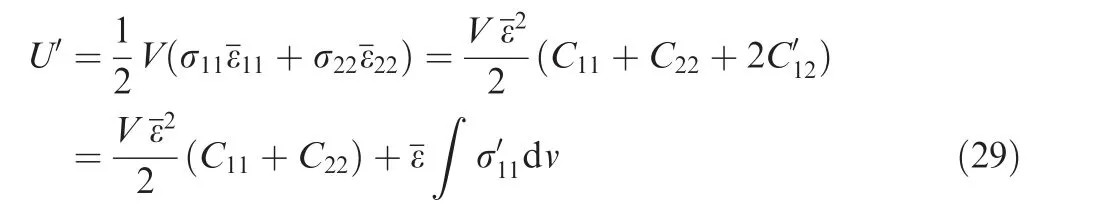
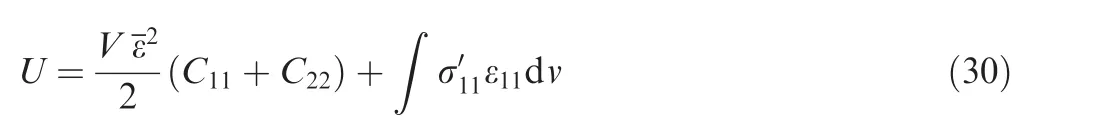
Comparison between Eqs.(31)and(32)shows that the inhomogeneity of the strain distribution is the main reason that causes the difference between the volume-average method and the energy method.Numerical results indicate that a relatively greater strain exists in the air zone than that in the wall,and the impact of the variation of the strain within the wall material is insignificant mainly due to its small volume fraction.

According to all the above analysis,the difference of the acquired effective properties between the volume-average method and the energy method,especially for the in-plane moduli,depends on the volume fraction of the air zone and the inhomogeneity of the strain field in the RVE cell.Moreover,all these factors mentioned relate to the wall thickness and cell geometries.

3.FE model

3.1.Convergence

The RVE cell chosen for a single-wall-thickness honeycomb structure is shown in Fig.2.As the vertical and oblique walls have the same thickness in the single-wall-thickness honeycomb,the cell geometric parameters in Fig.2(b)can bet1¼t,t2¼t=2.Three parameters includingt=l,h=land h determine the geometric configuration of the RVE cell.In later analysis,we focus on the most commonly used honeycombs,whoselandhremain the same asl=h=15.This absolute value is not significant as geometries only provide nondimensional coefficients for the effective properties.Moreover,the core height is set tohc=50 and it is in the range where the core height has little influence on effective properties according to Ref.2.

Fig.2 Single-wall-thickness honeycomb structure.

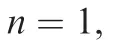
According to Eq.(3),elementary BCs will be applied to get an equivalent strain for the whole RVE cell.The essence of this computational homogeneous method is that the stiffness of the honeycomb structure is replaced by the stiffness of equivalent solids.Therefore,it is of great significance to simulate the deformation of the whole structure accurately.

3.2.Boundary conditions

Catapano and Montemurro2gave detailed BCs when taking into account the symmetries of the unit cell.As discussed by Hori and Nemat-Nasser,21the homogeneous stress BC and the homogeneous strain BC only provide the lower and upper bounds of effective moduli.The plane-remains-plane homogeneous BCs(or unit-displacement BCs)not only over-constrain the boundaries,but also violate the stress periodicity conditions.In theoretical analysis of the FE model proposed by Catapano and Montemurro2in the calculation for the in-plane shear modulusG12and the out-of-plane shear modulusG13,we found that the calculated value differs from different cell numbers.

3.2.1.G12under unit-displacement BCs

In this part,the accuracy of the RVE cell selected in Fig.2(b)to simulate the entire honeycomb structure under in-plane shear loading is discussed.The effect of cell numbers on the effective shear modulus is analyzed,based on which a new model(The new model is called Model 2,as the model shown in Fig.2(c)is called Model 1)is proposed to get more precise properties of in-plane shear under unit-displacement BCs.

When the honeycomb structure is subject to a shear loading in the 1-2 direction as shown in Fig.4,as mentioned before,bending deformation of the walls dominates in the honeycomb core.The deflection of the vertical walls and the rotation of the oblique walls together cause a deformation for the whole honeycomb core under 1-2 shear loading.From the previous theory in literature,22the proportion of the deflection of the vertical walls in the whole shear deformation on the boundary is

Therefore,the deflection of the vertical walls plays an important role in determining the effective in-plane shear modulus.

Fig.3 Convergence analysis of FE model.

Figs.4(a)and(b)illustrate the difference between a single RVE cell and a finite number of RVE cells under the same in-plane shear loading,which show that the local load on the vertical walls is not the same,thus causing different deflections.For a single RVE cell,the deflection of the vertical WallAE(CF)is

Fig.4 Honeycomb structure under shear loading along 1-2 direction.

While for the honeycomb core consisting of a finite number of RVE cells,the deflection of WallAE(CF)is

Load conditions on other parts of the RVE cell are the same,so there is no difference in the caused shear deformation.

From the above analysis,it can be seen that the discrepancy in the deflection of the vertical WallAE(CF)will result in a difference of the calculated effective shear modulus,and the result of a single RVE cell will be lower than that of the honeycomb core containing a finite number of RVE cells.The essence of this phenomenon is that the process of the homogeneous technique in this loading condition is replacing the shearing stiffness of the honeycomb core by the bending stiffness of the wall.The vertical WallAE(CF)in the chosen RVE cell has a half-wall thickness,which leads to a considerable reduction in the bending stiffness.However,the halved wall causes little section change of the RVE cell due to the very small volume fraction of the wall in the whole honeycomb core.For these reasons,the effective shear modulus of a single RVE cell is different from that of the whole honeycomb core.

To make a single RVE cell precisely simulate the deformation of a real honeycomb core with respect to in-plane shear,We introduce a new model named Model 2 on the basis of the FE model(Model 1)shown in Fig.2.Only a geometric change is done in Model 2 ast2=0.795tfromt2=t/2 in Model 1.For Model 2,the deflection of WallAE(CF)under the same in-plane loading is

This result has the same value of the deflection as in a finite number of RVE cells.

FE models containing different numbers of cells as respectivelyn=1,2,4,8,14,16 are established to evaluate the effect of the cell number on the effective in-plane shear modulus,and these models have the same BCs as those in Ref.2.

Calculations have been conducted on honeycombs of three geometries:

The FE results in Fig.5 indicate that for all the geometric situations,the effective in-plane shear modulus increases as more cells are included in the FE models,which is consistent with the previous analysis.Moreover,all the curves have a tendency of approaching a converged value that is closer to the modulus obtained by Model 2.Therefore,the results presented in Fig.5 can be a validation for the accuracy of Model 2 to simulate a real honeycomb core under in-plane shear loading.

Fig.5 Effective shear modulus vs number of RVE cells(Model 1 t2=t/2,Model 2 t2=0.795t).

3.2.2.G13under unit-displacement BCs

Similar to Section 3.2.1,the effect of the cell number on the effective out-of-plane shear modulus is analyzed,on the basis of which another new model called Model 3 is proposed to get more precise properties of the out-of-plane shear modulus in the 1-3 direction for the whole honeycomb core.

When the honeycomb structure is subject to a shear loading in the 1-3 direction as shown in Fig.6,the overall deformation of the honeycomb core is governed by the shear deformations of the vertical and oblique walls.We conduct an analysis on the shear flows inside each wall in a similar way used by Kelsey et al.23

For the single RVE cell presented in Fig.6(a)under 1-3 shear loading(with a shear stress s),the following equation is acquired by equilibrium conditions:

From Eq.(37),

For the real honeycomb core consisting of a finite number of RVE cells,under the consideration of periodicity,

From equilibrium conditions,

From Eqs.(39)and(40),we get

Comparison between Eqs.(38)and(41)shows that under the same shear loading in the 1-3 direction,the shear flow in WallAEas well asCFvaries in a single RVE cell and a finite number of RVE cells.In a single RVE cell,similar to the situation in the simulation of in-plane shear loading,WallsAEandCFsuffer higher shear flows than those in a finite number of RVE cells,leading to differences in the deformation for the entire honeycomb structure.The higher shear flowsqdandqecause the in-plane bending deformation of the oblique walls as shown in Fig.7 from the FE analysis of a single RVE cell.It can be seen that the extra bending deformation of the oblique walls is in a direction contributing to the 1-3 shear deformation,and FE results illustrate that this bending deformation is weakening as the cell number increases.For these reasons,a single RVE cell has a larger deformation than that of a finite number of RVE cells under the same loading owing to the bending deformation of the oblique walls,thus having a lower effective shear modulus in the 1-3 direction than that of a finite number of RVE cells.

In order to find an appropriate RVE model to simulate the deformation of the real honeycomb structure under the 1-3 direction shearing precisely,the thickness of the oblique walls is adjusted to suppress the extra bending deformation.The geometry of the proposed new model called Model 3 is determined according to the FE results shown in Fig.8.

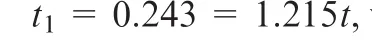
Fig.6 Honeycomb structure under shear loading along 1-3 direction.

Fig.7 In-plane bending deformation of oblique walls under shear loading along 1-3 direction.

Fig.8 Effective shear modulus along 1-3 direction vs thickness of oblique wall AB(BC).

Fig.9 Effective shear modulus vs number of RVE cells(Model 1 t1=t,Model 3 t1=1.215t).

Similar to the in-plane shear loading,FE models containing different numbers of cells as respectivelyn=1,2,4,8,14,16 are also used to evaluate the effect of the cell number on the effective out-of-plane shear modulus along the 1-3 direction,and honeycombs of three geometries are also taken into consideration,as shown in Fig.9.With the number of cells increasing,theeffectiveshearmodulusG13growsand approaches a converged value,as analyzed before.In addition,the converged value is very close to the result of Model 3 for all the three cell geometries.Therefore,this new model can provide a relatively more accurate value ofG13than that of Model 1 under this shear loading.

3.2.3.Periodic boundary conditions

As stated before,a single RVE cell cannot provide accurateG12andG13as those of the whole honeycomb core with unit-displacement BCs.However,when applied to periodic BCs,the effective properties remain constant with the cell number changing.Moreover,periodic BCs are required in determining the elastic properties of periodic media to ensure the periodicity of displacements and tractions on the boundary of the RVE.In order to generate a symmetrical mesh for the convenience of prescribing the periodic BCs,a whole unit cell is remained for FE analysis.

Mathematical expressions can be found in the literature by Whitcomb,24Xia,25Li and Wongsto,26which have been used in periodic media like unidirectional composites and plane and satin weave composites.Constraint equations(CEs)are utilized for periodic BCs of the rectangular solid RVE shown in Fig.1.These equations can be sorted into three categories,i.e.,equations for surfaces,edges,and vertices.

(1)Equations for surfaces

For surfaces perpendicular to 1-axis,i.e.,SurfacesEandF:

For surfaces perpendicular to 2-axis,i.e.,SurfacesAandB:

For surfaces perpendicular to 3-axis,i.e.,SurfacesCandD:

(2)Equations for edges

Two or three in Eqs.(42)-(44)are satisfied for nodes on the edges of the RVE.As these constraints are not independent,FE analysis cannot function properly if the CEs for edges are not considered separately as well as the CEs for vertices.

For edges parallel to the 1-axis,i.e.,Lineshd,ed,fb,andgc:

Similar equations can be given for edges parallel to the 2-axis and 3-axis.

(3)Equations for vertices

Pointdis fixed to avoid rigid-body motions of the RVE.Then seven CEs are defined for other vertices with the reference of Pointd.Equations for Pointsfandgare given here as examples:

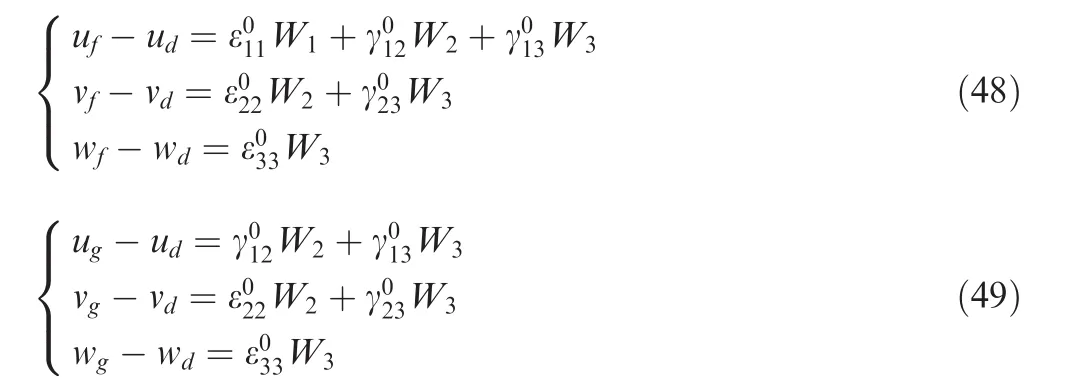
Periodic BCs are prescribed in the ABAQUS software combined with Python scripts.Python scripts are used to find nodes on surfaces,edges,and vertices,generate CEs for corresponding nodes in the mesh according to Eqs.(42)-(49),and submit jobs in the ABAQUS environment.After jobs are finished,post-processing Python scripts are executed to calculate effective moduli by both the volume-average method and the energy method.

4.Results

4.1.Volume-average stress and boundary stress

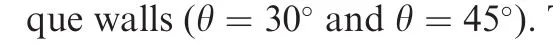
As discussed in Section 2.3,Eqs.(22)and(24)show an equality of the volume-average stress and the boundary stress,which is validated by the results in Table 1.Understanding such an equality,only the energy method and the volumeaverage method are operated in later FE analysis.

4.2.Results by energy method

In this part,we have compared the numerical results by the volume-average method and the energy method.Different cell geometries such as the wall thickness and the angle between vertical and oblique walls are taken into consideration to evaluate the supposed discrepancy between the two methods.

Fig.10 shows the numerical results of the energy method and the volume-average method at different wall thicknesses which range from 0.2 to 1.0 as the RVE cell has a dimension ofl=h=15.

It can be seen in Fig.10 that the three shear moduliG12,G13,andG23calculated by the volume-average method and the energy method are all nearly the same with a maximum difference of less than 3%.Since the shear moduli only relate to the diagonal elements in the stiffness matrix while calculated from the compliance matrix,this equilibrium of these three shear moduli can be a validation for Eq.(27).Nevertheless,for the elastic properties relate to non-diagonal components(i.e.E1,E2,E3,v12,v13,andv23),divergences exist between the volume-average method and the energy method.

Fig.10(d)shows that the volume-average method gets the same results as those of Malek&Gibson’s model,which validates our proper use of the volume-average method.

As stated in Section 2.3,the main motivation that we put forward this energy method is the supposed discrepancy in the calculation ofC12.It has been proven in Section 2.3 that an inaccurate calculation ofC12in the volume-average method leads to an inaccurate strain energy under bi-axial BCs.The discrepancy of the strain energy in each model of unit cells is presented in Fig.11.It can be seen that the discrepancy remains 1.3%–1.6%within our computing range.Although the relative error remains nearly constant,the absolute value increases as the wall thickness increases.

For the in-plane elastic propertiesE1andE2,within the range of calculation,the absolute value of the discrepancy between the two methods varies with the cell wall thickness increasing.However,in these geometries,as the wall thickness increases,the relative error between these two methods is slightly changed from nearly 8%to 6%.This follows from the fact that the discrepancy of the strain energy under biaxial BCs remains almost the same as shown in Fig.11,representing the difference of non-diagonal elements in the stiffness matrix.The numerical results forE3have little discrepancy due to the homogeneous strain and stress fields of the whole honeycomb structure under uniaxial tensions in the 3 directions.As shown in Eqs.(31)and(32),uniform strain and stress fields do not lead to a difference betweend1andd2.The curves ofv13andv23show a similar tendency to those of the in-plane moduliE1andE2,which conforms to the hypothesis proposed by Malek and Gibson asv31=v32=vwherevis the Poisson’s ratio of the cell wall material.

Table 1 Comparison between boundary method and volume-average method.

Similar conclusions can be drawn from results illustrated in Fig.12 with those in Fig.10.On one hand,approximately the same values for three shear moduli are acquired by the volume-average and energy methods.On the other hand,divergence exists for other properties related to non-diagonal components of the stiffness matrix and this divergence varies with different cell geometries.

Results in Fig.12 show that the deviation of effective properties obtained by both the volume-average method and the energy method varies as the angle changes from 30?to 60?.Nevertheless,effective elastic properties obtained using the energy method remain at values that are lower than those using the volume-average method.According to the experiment data of a regular honeycomb(h/l=1)provided in Ref.2which are also slightly lower than their numerical results(based on the volume-average method),results by the energy method may provide more accurate values.In a consistency with Fig.10,numerical results at angles of 45?and 60?also indicate a slight increase of the discrepancy between the two methods as the wall thickness increases.

Fig.10 Numerical results of energy method and volume-average method vs wall thickness.

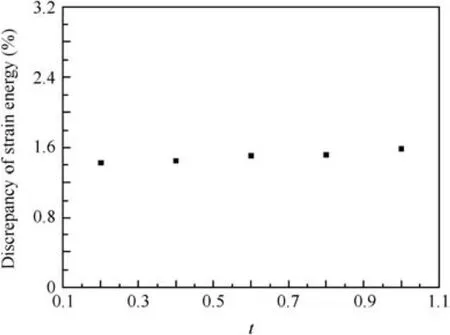
Fig.11 Discrepancy of strain energy of honeycomb cores under bi-axial BCs.

From the results in Figs.10–12,it can be concluded that the energy method gets different values of effective properties of a thin-wall thickness honeycomb from those of the volumeaverage method regardless of the variation of the angle between vertical and oblique walls.It can be proven that the discrepancy of the strain energy under bi-axial BCs can be considered as a symbol for the difference of the two methods in determining effective properties.The inaccuracy in calculating the strain energy shows the inaccurate moduli acquired by the volume-average method.

Fig.12 Numerical results of energy method and volume-average method vs angle between vertical and oblique walls.

4.3.Comments on discrepancy

As shown in Fig.11,the discrepancy of the strain energy under bi-axial BCs between the volume-average method and the energy method is very small.Here,three 4-element models are established.

On one hand,the 4-element models show a possible big deviation of the strain energy between the two methods,which represents the need of performing numerical bi-axial tests.On the other hand,different models may have different inhomogeneity of the strain distribution,which we think results in the discrepancy between the two methods.

The models are shown in Fig.13.Four C3D8I elements are utilized to form the models.Each element is assigned specific material properties that are preset in Table 2.The material properties are set to present the supposed discrepancy betweend1andd2according to their expressions analyzed in Eqs.(31)and(32).

The results of these 4-element models are shown in Table 3.From the results,it can be found that the deviation betweend1andd2can be larger than 50%in Model 3.However,sinceC12is about one sixth ofC11andC12,the deviation of the strain energy reduces to 7.28%.The 4-element models can prove the discrepancy of the strain energy under bi-axial BCs.

It can also be seen that the deviation betweend1andd2varies in the three models as well as the deviation of the strain energy.The maximum and minimum strains are also listed in Table 3.It can be seen that in the 4-element models,the deviation betweend1andd2increases with the inhomogeneity of strain increasing.

From these results,we get:

(1)The discrepancy between the two methods varies with different problems.

(2)The inhomogeneity of the strain distribution influences that discrepancy.

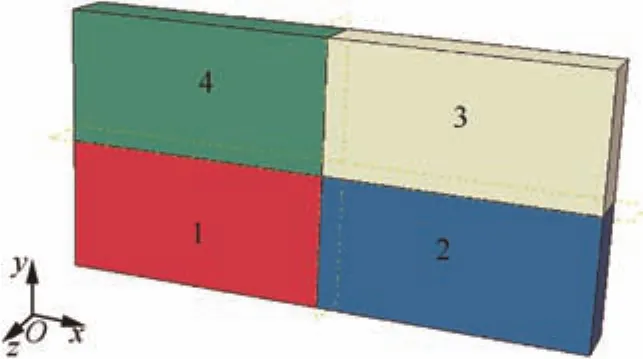
Fig.13 Four-element model composed of 4 materials.

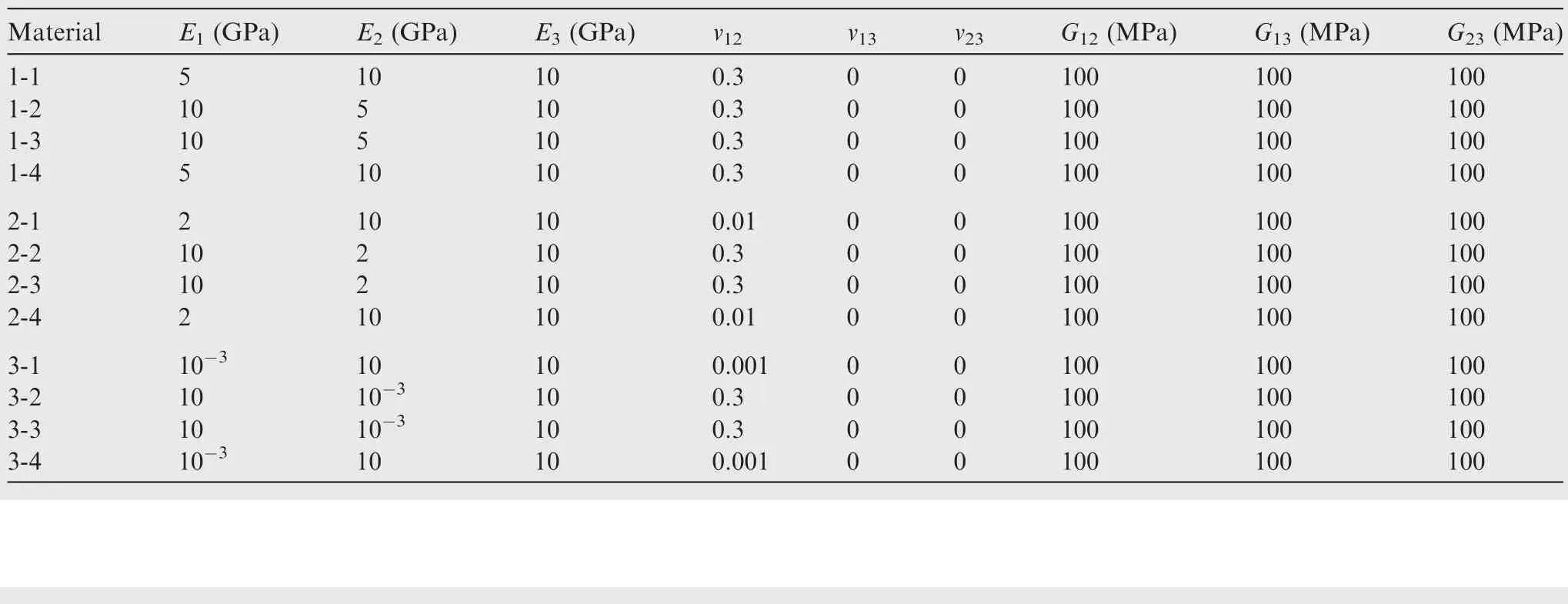
Table 2 Material properties used in 4-element models.

Table 3 Results of 4-element models.

5.Conclusions

(1)An equality for the volume-average method and the boundary method previously used in predicting the effective moduli is validated,and this equality remains constant as cell geometries and cell forms vary.

(2)An energy method is proposed based on the equality of the strain energy of the RVE cell and the corresponding homogeneous solid.Analysis has been done on the discrepancy between the energy method and the volumeaverage method.Numerical results show that the energy method obtains values of effective properties closer to experimental results for in-plane moduli.

1.Goswami S.On the prediction of effective material properties of cellular hexagonal honeycomb core.J Reinf Plast Compos2006;25(4):393–405.

2.Catapano A,Montemurro M.A multi-scale approach for the optimum design of sandwich plates with honeycomb core.Part I:Homogenization of core properties.ComposStruct2014;118:664–76.

3.Catapano A,Jumel J.A numerical approach for determining the effective elastic symmetries of particulate-polymer composites.Compos Part B Eng2015;78:227–43.

4.Montemurro M,Catapano A,Doroszewski D.A multi-scale for the simultaneous shape and material optimization of sandwich panels with cellular core.Compos Part B Eng2016;91:458–72.

5.Malek S,Gibson L.Effective elastic properties of periodic hexagonal honeycombs.Mech Mater2015;91(1):226–40.

6.Shi GY,Tong P.Equivalent transverse shear stiffness of honeycomb cores.Int J Solids Struct1995;32(10):1383–93.

7.Li K,Gao XL,Subhash G.Effects of cell shape and cell wall thickness variations on the elastic properties of two-dimensional cellular solids.Int J Solids Struct2005;42(5–6):1777–95.

8.Papka SD,Kyriakides S.Experiments and full-scale numerical simulations of in-pane crushing of a honeycomb.Acta Mater1998;46(8):2765–76.

9.Yu W,Tang T.Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials.Int J Solids Struct2007;44(11–12):3738–55.

10.Sun CT,Vaidya RS.Prediction of composite properties from a representative volume element.Compos Sci Technol1996;56(2):171–9.

11.Hollister SJ,Kikuchi N.A comparison of homogenization and standard mechanics analyses for periodic porous composites.Comput Mech1992;10(2):73–95.

12.Karakoc A,Freund J.Experimental studies on mechanical properties of cellular structures using Nomex?honeycomb cores.Compos Struct2012;94(6):2017–24.

13.Shen GL,Hu GK,Liu B.Mechanics of composite materials.2nd ed.Beijing:Tsinghua University Press;2013,p.45–6.

14.Hill R.Elastic properties of reinforced solids:Some theoretical principles.J Mech Phys Solids1963;11(5):357–72.

15.Beer FP,Johnston Jr ER,DeWolf JT,Mazurek DF.Mechanics of materials.6th ed.Columbus,OH:McGraw-Hill Education;2012,p.732–4.

16.Gibson LJ,Ashby MF,Schajer GS,Robertson CI.The mechanics of two-dimensional cellular materials.Proceed Roy Soc Lond Ser A,Math Phys Sci1982;382(1782):25–42.

17.Burton WS,Noor AK.Assessment of continuum models for sandwich panel honeycomb cores.Comput Method Appl Mech1997;145(3):341–60.

18.Belytschko T,Liu WK,Kennedy JM.Hourglass control in linear and nonlinear problems.Comput Method Appl Mech1984;43(3):251–76.

19.Hexcel Corporation.HexWebTMhoneycomb attributes and properties—A comprehensive guide to standard Hexcel honeycomb materials,configurations,and mechanical properties[Internet];1999.Available from:http://www.hexcel.com/resources/technology-mauals.[updated 2016,cited 2016 Jan 4].

20.Kutz M.Handbook of materials selection.New York:John Wiley&Sons,Inc.;2002,p.100–3.

21.Hori M,Nemat-Nasser S.On two micromechanics theories for determining micro-macro relations in heterogeneous solids.Mech Mater1999;31(10):667–82.

22.Wang YJ.Note on the in-plane shear modulus of honeycomb structures.Chin J Appl Mech1993;10(1):93–7[Chinese].

23.Kelsey S,Gellatly RA,Clark BW.The shear modulus of foil honeycomb cores.AircrEngAerospTecnol1958;30(10):294–302.

24.Whitcomb JD,Chapman CD,Tang X.Derivation of boundary conditions for micromechanics analyses of plain and satin weave composites.Surf Sci2000;34(9):724–47.

25.Xia Z,Zhang Y,Ellyin F.A unified periodical boundary conditions for representative volume elements of composites and applications.Int J Solids Struct2003;40(8):1907–21.

26.Li S,Wongsto A.Unit cells for micromechanical analyses of particle-reinforced composites.Mech Mater2004;36(7):543–72.

25 January 2016;revised 11 August 2016;accepted 29 December 2016

Available online 16 February 2017

*Corresponding author.

E-mail address:07343@buaa.edu.cn(Z.Guan).

Peer review under responsibility of Editorial Committee of CJA.