2017年高考数列经典问题聚焦

■陕西省洋县中学 刘大鸣(特级教师)

2017年高考数列经典问题聚焦

■陕西省洋县中学 刘大鸣(特级教师)

2017年高考对数列的考查主要围绕“等差和等比数列的通项及求和、一般数列的切入点、用公式求和、裂项相消法求和、错位相减法求和、求证数列不等式中的函数法、数学归纳法、迭代法和累乘法等以及数列的新定义问题”等展开,凸显了数列的工具性和应用性。

聚焦1 基本量法求解等差与等比数列

(1)(2017年全国Ⅰ,理4)记Sn为等差数列{an}的前n项和。若a4+a5=24,S6=48,则{an}的公差为( )。

A.1 B.2 C.4 D.8

(2)(2017年课标3,理14)设等比数列{an}满足a1+a2=-1,a1-a3=-3,则a4=。

解析:借助等差(比)数列的通项及求和公式构建方程组求解,可巧用整体思维简化求解。

(1)(法1:基本量法构建方程组)设公差为d,a4+a5=a1+3d+a1+4d=2a1+d=6a1+15d=48,

(法2:利用等差数列的性质)因为S6=3(a3+a4)=48,即a3+a4=16,则(a4+a5)-(a3+a4)=24-16=8,即a5-a3=2d=8,解得d=4,故选C。

(2)(基本量法构建方程组)设等比数列的公比为q,很明显q≠-1,结合等比数列的通项公式和题意可得方程组:q=-2,代入①可得a1=1,由等比数列的通项公式可得:a4=a1q3=-8。

感悟:等差、等比数列各有五个基本量、两组基本公式,这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化为解关于基本量的方程(组),有意识地应用等差、等比数列的性质可以简化运算,应注意“巧用性质、整体考虑、减少运算量”。

聚焦2 用一般数列的切入点求解数列通项及应用裂项相消法求和

(2017年全国Ⅲ,文17)设数列{an}满足a1+3a2+…+(2n-1)an=2n。

(1)求{an}的通项公式;(2)求数列的前n项和。

解析:把握a1+3a2+…+(2n-1)an=2n为Sn的形式,构建方程组求解通项,再应用裂项相消法求和。

(1)由a1+3a2+…+(2n-1)an=2n可得得n≥2时,a1+3a2+…+(2n-3)an-1=2(n-1),再作差得,验证n=1时也满足。

则{an}的通项公式

感悟:对一般数列的切入点an=的应用中,凸显方程组观念及降元意识和分类讨论的方法,一定要检验当n=1时是否满足n≥2的an,否则很容易出现错误。

聚焦3 等比数列中连续三项和Sn+1,Sn,Sn+2为等差数列的判断证明

(2017年全国Ⅰ,文17)记Sn为等比数列{an}的前n项和,已知S2=2,S3=-6。

(1)求{an}的通项公式;

(2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列。

解析:由等比数列通项公式构建方程组解得q=-2,a1=-2,进而求通项公式;利用等差中项证明Sn+1,Sn,Sn+2成等差数列。

(1)设{an}的公比为q。由题设可得,解得q=-2,a1=-2,故{an}的通项公式为an=(-2)n。

感悟:等比数列中连续三项和Sn+1,Sn,Sn+2为等差数列。

证明等差或等比数列常用方法有:① 定义法:an-an-1=d(d为常数)(n∈N*)⇔{an}是等差数列=q(an≠0,q≠0)⇔{an}是等比数列。

②中项法:2an=an+1+an-1⇔{an}是等差数列;an2=an+1an-1(an≠0)⇔{an}是等比数列。

聚焦4 直接用等比或等差数列求和公式求和

(2017年北京,文15)已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5。

(1)求{an}的通项公式;

(2)求和:b1+b3+b5+…+b2n-1。

解析:先由题设及等差和等比数列通项公式构建方程组确定两个通项公式,再利用等比数列求和公式求和。

(1)设公差为d,由a1=b1=1,a2+a4=10得1+d+1+3d=10,则d=2,所以an=a1+(n-1)d=2n-1。

(2)设{bn}的公比为q,则{b2n-1}依然是等比数列,并且公比是q2。

由b2·b4=a5,b1=1,a5=9可得qq3=9,所以q2=3。

所以{b2n-1}是以b1=1为首项,公比为q2=3的等比数列。

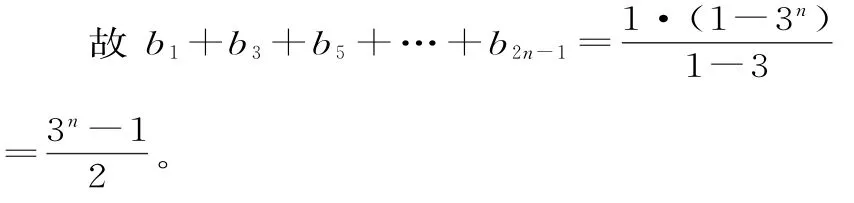
感悟:应用等差或等比数列的前n项和公式求和时,要依据数列的特征,判断数列的类型,确定首项 、公差或公比以及项数代入公式。

聚焦5 等差数列中充要条件的判断

(2017年浙江,6)已知等差数列{an}的公差为d,前n项和为Sn,则“d＞0”是“S4+S6＞2S5”的( )。

A.充分不必要条件

B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

解析:借助等差数列的求和公式坚持推理进行判断。

由S4+S6-2S5=10a1+21d-2(5a1+10d)=d,可知当d＞0时,则S4+S6-2S5＞0,即S4+S6＞2S5。反之,S4+S6＞2S5⇒d＞0,所以为充要条件,应选C。

感悟:本题考查等差数列中充分必要性的判断。通过前n项和公式的套入与简单运算,可知S4+S6-2S5=d,结合充分必要性的判断方法,若p⇒q,则p是q的充分条件,若p⇐q,则p是q的必要条件。该题实质为

“d＞0”⇔“S4+S6-2S5＞0”。

聚焦6 应用“错位相减法”求解等差与等比对应项的积构成的数列的和

(2017年天津,理18)已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4。

(1)求{an}和{bn}的通项公式;

(2)求数列{a2nb2n-1}的前n项和(n∈N*)。

解析:由题设构建等差数列首项a1和公差d及等比数列的公比q的方程组确定2个数列的通项公式;等差与等比对应项的积构成的数列求和选用“错位相减法”。

(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q。

由已知b2+b3=12,得b1(q+q2)=12,而b1=2,所以q2+q-6=0。

又因为q＞0,解得q=2。所以,bn=2n。

由b3=a4-2a1,可得3d-a1=8。①

由S11=11b4,可得a1+5d=16。②

联立①②,解得a1=1,d=3,由此可得an=3n-2。

所以,数列{an}的通项公式为an=3n-2,数列{bn}的通项公式为bn=2n。

(2)设数列{a2nb2n-1}的前n项和为Tn。

由a2n=6n-2,b2n-1=22n-1,得a2nb2n-1=(3n-1)×4n。

故Tn=2×4+5×42+8×43+…+(3n-1)×4n。

4Tn=2×42+5×43+8×44+…+(3n-4)×4n+(3n-1)×4n+1。

上述两式相减,得-3Tn=2×4+3×42+3×43+…+3×4n-(3n-1)×4n+1

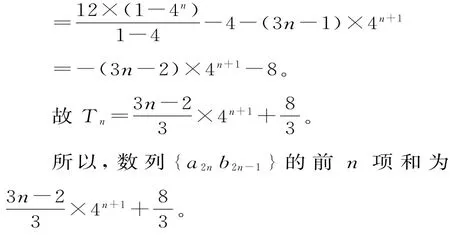
感悟:2017年山东卷理科第19题、文科第18题,2017年天津卷文科第18题均考查“错位相减法”求和。一般地,如果数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,用错位相减法求和,写出“Sn”与“qSn”的表达式,将两式“错项对齐”进行相减,中间项两两结合提公差构成n-1项的等比数列的和,再用等比数列求和公式化简整理。

聚焦7 新定义数列中的等差数列的证明

(2017年江苏,19)对于给定的正整数k,若数列{an}满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n(n＞k)总成立,则称数列{an}是“p(k)数列”。

(1)证明:等差数列{an}是“p(3)数列”;

(2)若数列{an}既是“p(2)数列”,又是“p(3)数列”,证明:{an}是等差数列。

解析:把握新定义“p(k)数列”。实质为一个数列连续的2k+1项的和满足恒等式的意义,可借助等差数列的定义法求证。

(1)验证等差数列{an}是“p(3)数列”,因为{an}是等差数列,设其公差为d,则an=a1+(n-1)d。

从而,当n≥4时,an-k+an+k=a1+(nk-1)d+a1+(n+k-1)d=2a1+2(n-1)·d=2an,k=1,2,3。

所以an-3+an-2+an-1+an+1+an+2+an+3=6an,由“p(k)数列”的定义知等差数列{an}是“p(3)数列”。

(2)依据“p(2)数列”和“p(3)数列”的意义求证{an}是等差数列。

数列{an}既是“p(2)数列”,又是“p(3)数列”,因此:

当n≥3时,an-2+an-1+an+1+an+2=4an。①

当n≥4时,an-3+an-2+an-1+an+1+an+2+an+3=6an。②

由①对n-1成立可得an-3+an-2=4an-1-(an+an+1)。③

类比有an+2+an+3=4an+1-(an-1+an)。④

将③④代入②,得an-1+an+1=2an,其中n≥4。

所以a3,a4,a5,…是等差数列,设其公差为d'。

在①中,取n=4,则a2+a3+a5+a6=4a4,所以a2=a3-d'。

在①中,取n=3,则a1+a2+a4+a5=4a3,所以a1=a3-2d'。

所以数列{an}是等差数列。

感悟:本题借助等差数列定义及通项公式验证新定义的属性,由新定义的属性证明{an}为等差数列,关键在构建方程组。

当n≥3时,an-2+an-1+an+1+an+2=4an。①

当n≥4时,an-3+an-2+an-1+an+1+an+2+an+3=6an。②

对①取n-1得到一个等式,再类比得到另一个等式,代入②变形得到an-1+an+1=2an,同时还需要对前2项特殊赋值,进而得到证明。

聚焦8 用等比和等差数列求和解决实际应用问题

(2017年全国Ⅰ,理12)几位大学生响应国家的创业号召,开发了一款应用软件。为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推。求满足如下条件的最小整数N:N＞100且该数列的前N项和为2的整数幂。那么该款软件的激活码是( )。

A.440 B.330 C.220 D.110

解析1:把握元素自然分组和等比数列的特征,可利用等差、等比数列求和,根据题设构建二元不定方程探究最小的正整数解。

设首项为第1组,接下来两项为第2组,再接下来三项为第3组,依此类推。设第n组的项数为n,则n组的项数和为

解析2:把握元素自然分组和等比数列的特征,求和解不等式探究最小的正整数解。

由题意得,数列如下:

1,

1,2,

1,2,4,

……

1,2,3,…,2k-1,

……

所以k=2t-3≥14,则t≥5,取t=5,此时k=25-3=29。

感悟:本题巧妙地将实际问题与等差数列、等比数列的通项与求和及二元不定方程正整数解融合在一起。解题时首先需要读懂题目所表达的具体含义,以及观察所给定数列的特征,进而判断出该数列的通项并求和。难点在于数列里面套数列,第一个数列的和又作为下一个数列的通项,而且最后几项并不能放在一个数列中,需要进行判断。

聚焦9 数列和不等式求证中的“函数法”“数学归纳法”“累加法”和“放缩法”

(2017年浙江,22)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*)。

当n∈N*时,试证明:(1)xn＞xn+1＞0,

证明:(1)构造函数用单调性或用数学归纳法证明。

(法1)构造函数法。根据题设递推关系xn=xn+1+ln(1+xn+1)构造函数,令函数f(x)=x+ln(1+x),则易得f(x)在[0,+∞)上为增函数。

又xn=f(xn+1),若xn＞0⇒f(xn+1)＞f(0)=0恒成立,故xn+1＞0。

对xn+1＜xn的证明可用作差法。

由xn=xn+1+ln(1+xn+1)可知xn＞0。

由xn-xn+1=xn+1+ln(1+xn+1)-xn+1=ln(1+xn+1)＞0,得xn＞xn+1。

所以0＜xn+1＜xn。

(法2)用数学归纳法证明:xn＞0。

当n=1时,x1=1＞0。

假设当n=k时,xk＞0,那么当n=k+1时,若xk+1≤0,则xk=xk+1+ln(1+xk+1)≤0,与假设矛盾,故有xk+1＞0。

综上xn＞0(n ∈N*)成立。而xn=xn+1+ln(1+xn+1)＞xn+1＞0,因此,xn＞xn+1＞0。

(2)根据待证不等式的特征由题设构造xnxn+1-4xn+1+2xn=xn2+1-2xn+1+(xn+1+2)ln(1+xn+1)≥0,再构造函数证明。

由xn=xn+1+ln(1+xn+1)＞xn+1＞0得-4xn+1=4ln(1+xn+1)-4xn,2xn=2xn+1+2ln(1+xn+1),xnxn+1=xn2+1+xn+1ln(1+xn+1),则xnxn+1-4xn+1+2xn=xn2+1-2xn+1+(xn+1+2)ln(1+xn+1),构造函数f(x)=x2-2x+(x+2)ln(1+x),用导数法可证函数f(x)在(0,+∞)上单调递增,则f(x)≥f(0)=0,因此f(xn+1)=xn2+1-2xn+1+(xn+1+2)ln(1+xn+1)≥0,故xnxn+1-4x+2x≥0,2x-x＜,即不

n+1nn+1n等式

(3)可以巧用(2)的结论,利用迭代法和累乘法证明不等式。详细证明略。

感悟:本题主要考查数列的概念、递推关系与单调性等基础知识,不等式及其应用,同时考查同学们的推理论证能力、分析问题和解决问题的能力,属于难题。证明数列不等式常用的方法有:(1)数学归纳法或函数法以及放缩法;(2)构造函数,利用函数的单调性证明;(3)由递推关系采用迭代法和累乘法证明。

(责任编辑 徐利杰)