具有无穷平衡点的新混沌系统动力学分析与振动控制
孙常春, 陈仲堂, 侯祥林
(1. 沈阳建筑大学 理学院, 沈阳 110168; 2. 沈阳建筑大学 机械工程学院, 沈阳 110168)
具有无穷平衡点的新混沌系统动力学分析与振动控制
孙常春1, 陈仲堂1, 侯祥林2
(1. 沈阳建筑大学 理学院, 沈阳 110168; 2. 沈阳建筑大学 机械工程学院, 沈阳 110168)
提出了一个新的三维混沌系统,对它奇特的动力学行为展开了理论分析和数值仿真。此系统具有无穷多个平衡点,全部位于一个平面的双曲线上。在状态和参数的组合变换下,系统能生成对称的隐藏吸引子。在双参数的对称变换下,混沌具有不变性。同时,系统轨道出现了大幅度的跃迁现象。最后,设计出单参数调节的线性状态反馈控制器,在有限时间内消除混沌。
新混沌系统; 无穷平衡点; 隐藏吸引子; 动力学分析; 振动控制
在自然界中,存在无数的混沌现象。随着科学研究的不断进展,大量连续的新混沌系统逐渐被发现和认知[1-6]。然而,绝大部分的科学研究主要集中在探索和发现三维二次多项式混沌系统,这类系统的主要特点是微分方程结构相对简单,易于动力学分析。除了这类典型的混沌系统外,自然界中还存在着许多其它类型的新混沌系统,目前,关于三维二次多项式以外、而且具有隐藏吸引子的新混沌系统的研究,并不多见。同时,近五年,关于隐藏吸引子的问题已成为混沌研究领域的热点[7-8]。
由于非线性振动[9]在实际工程中的广泛存在[10],仅研究三维二次多项式混沌系统,必将无法揭示和发现混沌振动的某些特殊动力学行为。因此,研究具有特殊性质或动力学行为的其它类型新混沌系统,对自然科学的进一步发展和实际工程问题的解决,均具有重大的理论意义和科学价值。文献[11]特别明确指出:针对混沌动力学的研究,是目前非线性动力学领域的前沿课题。
同时,由于隐藏吸引子的存在,导致突发的大幅度混沌振动,将可能带来灾难性的后果。例如:由突发的混沌振动引起的机械转子的失效等。因此,研究具有突发的大幅度振动行为的新混沌系统,具有重要的现实意义和应用价值。当混沌振动有害时,如何快速消除混沌,保持系统稳定是混沌控制领域研究的重点。迄今为止,针对混沌控制问题,已经取得了一些重要的研究成果[12-15]。
本文提出了一个具有隐藏吸引子的新混沌系统,它不属于三维二次多项式混沌系统。此新系统具有无穷多个平衡点,而且所有的平衡点均落在一个平面的双曲线上。在系统的状态和参数的组合变换下,系统能生成两个对称的隐藏吸引子。在系统的双参数对称变换下,混沌吸引子完全相同,即:混沌具有不变性。同时,借助计算机的数值仿真,观测到了系统轨道的突然大幅度跃迁现象,突发的大幅度混沌振动随之出现。
本文所研究的这类具有隐藏吸引子的混沌振动中,振幅的突然剧烈增加,将可能对大型工程机械产生巨大的破坏力,进而导致系统突发故障。因此,针对此类混沌振动系统的研究,将有助于预防不明原因引起的机械振动故障和有效保护大型机械系统的正常运转,进而减少经济损失。
最后,本文给出了这类混沌振动的有效控制方法。在不改变系统平衡点数量(无穷多个)和空间位置的情况下,设计出具有单参数调节功能的线性状态反馈控制器,每次通过调节控制参数,来分别控制系统的状态到达不同的平衡点,而且能通过对此单参数的调节,来调控系统状态的收敛速度,保证混沌振动在有限时间内消除,即:实现了具有隐藏吸引子的新混沌系统的调节控制。本文提出的控制方法,将有助于解决由隐藏吸引子带来的突发混沌振动问题,进而有效保护大型机械工程的运转,从而为解决类似工程振动问题,提供了良好的借鉴和启示。
1 新混沌系统的微分方程描述
首先,提出一个新的三维混沌系统,由下列微分方程描述:
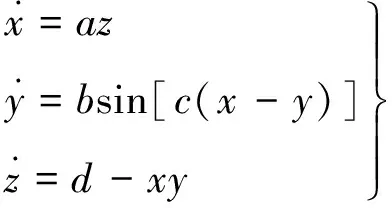
(1)
式中:x,y,z是系统的状态变量;a,b,c和d是系统的四个参数;a,b,c均是非零的实数,即:abc≠0;d>0是正的实数。
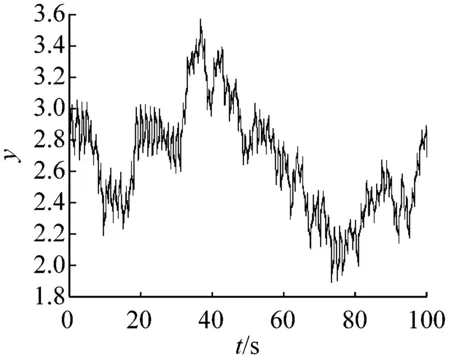
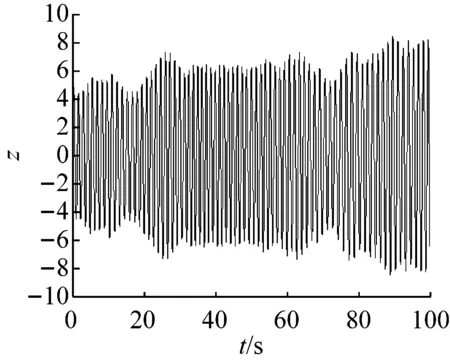
当参数a=8,b=3,c=8,d=20,初始状态(x0,y0,z0)=(-1,3,-1),仿真时间t1=100 s时,系统(1)能生成一个特殊的新混沌吸引子。此吸引子在各个坐标面上的投影如图1所示,系统状态的混沌时间序列,如图2所示。

(a)
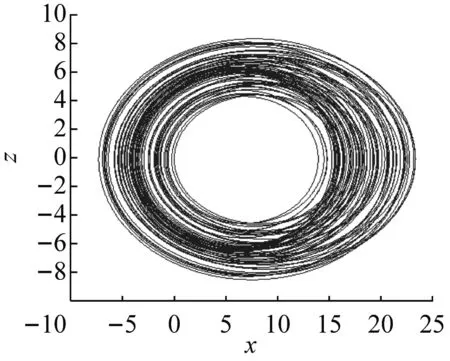
(b)
(c)
(a)
(b)
(c)
2 新混沌系统的动力学分析
为了进一步研究新混沌系统式(1)所具有的特殊性质和奇特的动力学行为,对系统式(1)进行了相应的理论分析,并借助计算机数值仿真,来深刻揭示它与已发现的全部混沌系统的不同之处。
2.1系统的平衡点
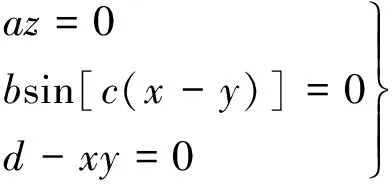
(2)
由于abc≠0,进一步有方程组成立:
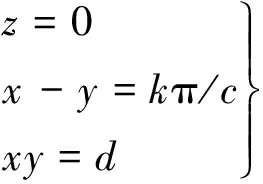
(3)
式中:k∈Z,Z是由全体整数构成的集合。
令
x-y=q
(4)
其中:q=kπ/c。
将方程组式(3)和方程式(4)进行联立,得到下面一元二次方程:
y2+qy-d=0
(5)
由于d>0,故
Δ=q2+4d>0
(6)
先后解出变量y和x:
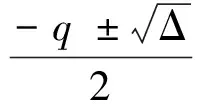
(7)
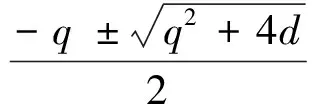
(8)
得到系统(1)的平衡点如下:
由于q=kπ/c和k∈Z,故系统式(1)具有无穷多个平衡点。而且,全部平衡点均落在平面z=0上的双曲线xy=d上。
2.2对称共存的隐藏吸引子
由于系统式(1)具有无穷多个平衡点,故系统式(1)生成的吸引子是隐藏吸引子。
在系统的状态和参数的两种组合变换
T1:(x,y,z,a,b,c,d)→(-x,-y,z,-a,b,c,d)
T2:(x,y,z,a,b,c,d)→(-x,-y,z,-a,-b,-c,d)
下,系统式(1)均存在自然的对称性。
上述组合变换进一步表明:如果系统式(1)在一组参数a,b,c,d和初始状态(x0,y0,z0)下是混沌的,那么系统式(1)在一组参数-a,b,c,d(或-a,-b,-c,d)和初始状态(-x0,-y0,z0)下也是混沌的。
同时表明:对称的隐藏吸引子是共同存在的,即:
1) 共存的隐藏吸引子在平面z=0上的投影关于原点对称;
2) 共存的隐藏吸引子在平面y=0上的投影关于z轴对称;
3) 共存的隐藏吸引子在平面x=0上的投影关于z轴对称。
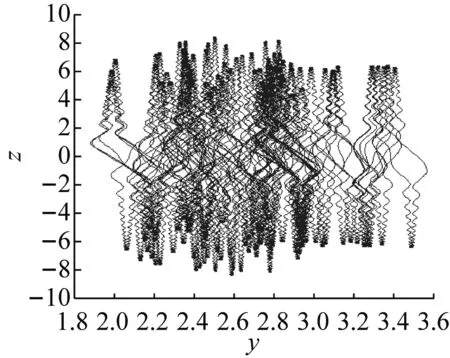
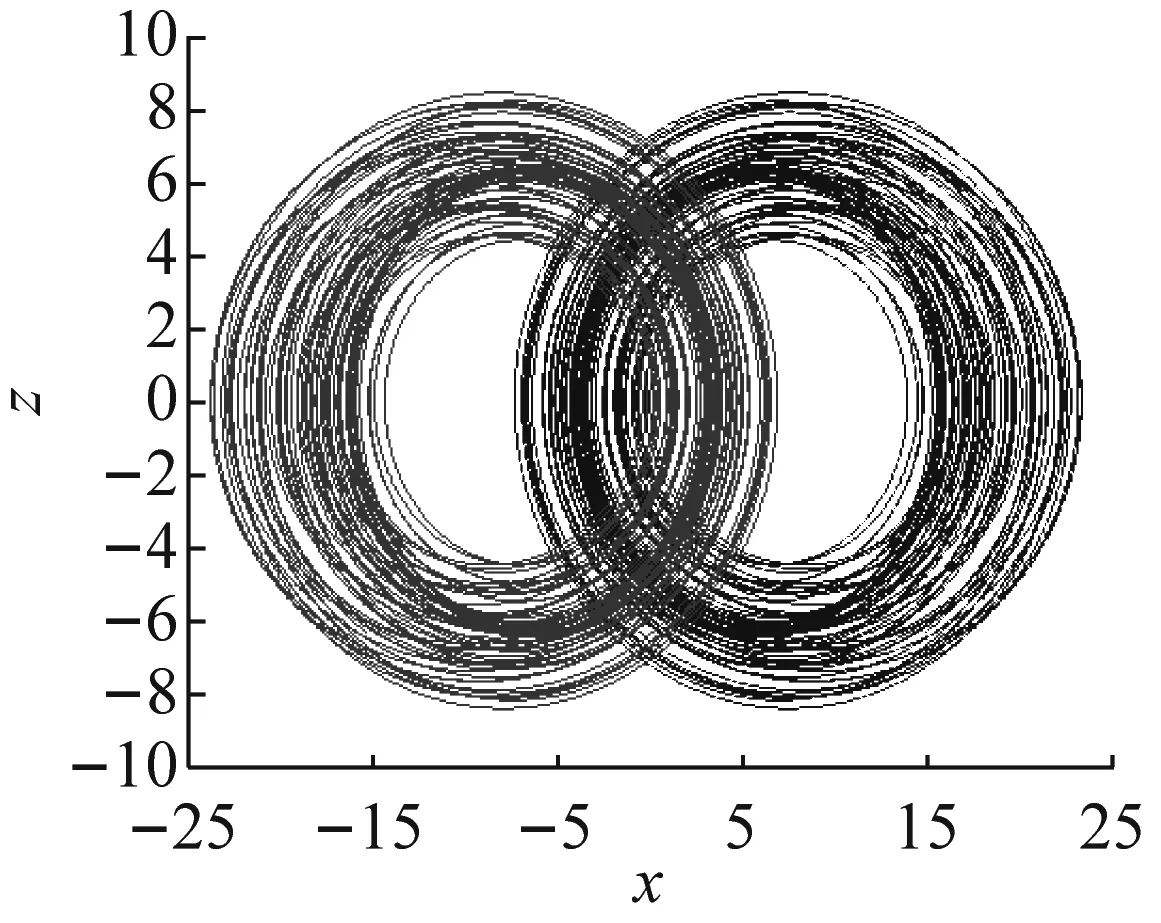
参数a=8,b=3,c=8,d=20和初始状态(x0,y0,z0)=(-1,3,-1)时,系统式(1)能生成隐藏吸引子(图3中右侧吸引子)。
当参数a=-8,b=3,c=8,d=20(或a=-8,b=-3,c=-8,d=20)和初始状态(x0,y0,z0)=(1,-3,-1)时,系统(1)也能生成隐藏吸引子(图3中左侧吸引子)。
显然,右侧和左侧吸引子是对称共存的。
(a)
(b)
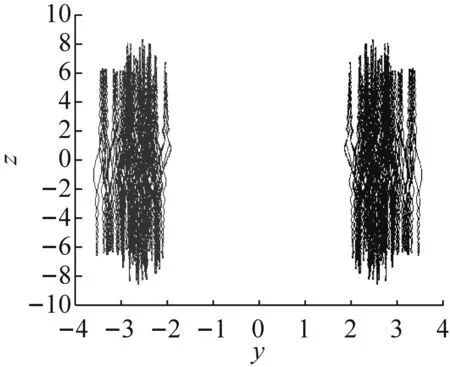
(c)
2.3双参数对称的混沌不变性
由于系统式(1)的第二个方程中的右边bsin[c(x-y)]=-bsin[-c(x-y)],故在参数变换
T3:(a,b,c,d)→(a,-b,-c,d)
下,系统式(1)的微分方程不变,故生成的混沌具有不变性。其中:b和c是对称的双参数。
上述参数变换进一步表明:如果系统式(1)在一组参数a,b,c,d和初始状态(x0,y0,z0)下是混沌的,那么系统式(1)在一组参数a,-b,-c,d和初始状态(x0,y0,z0)下也是混沌的,而且生成完全相同的混沌吸引子。
2.4系统轨道的突然大幅度跃迁
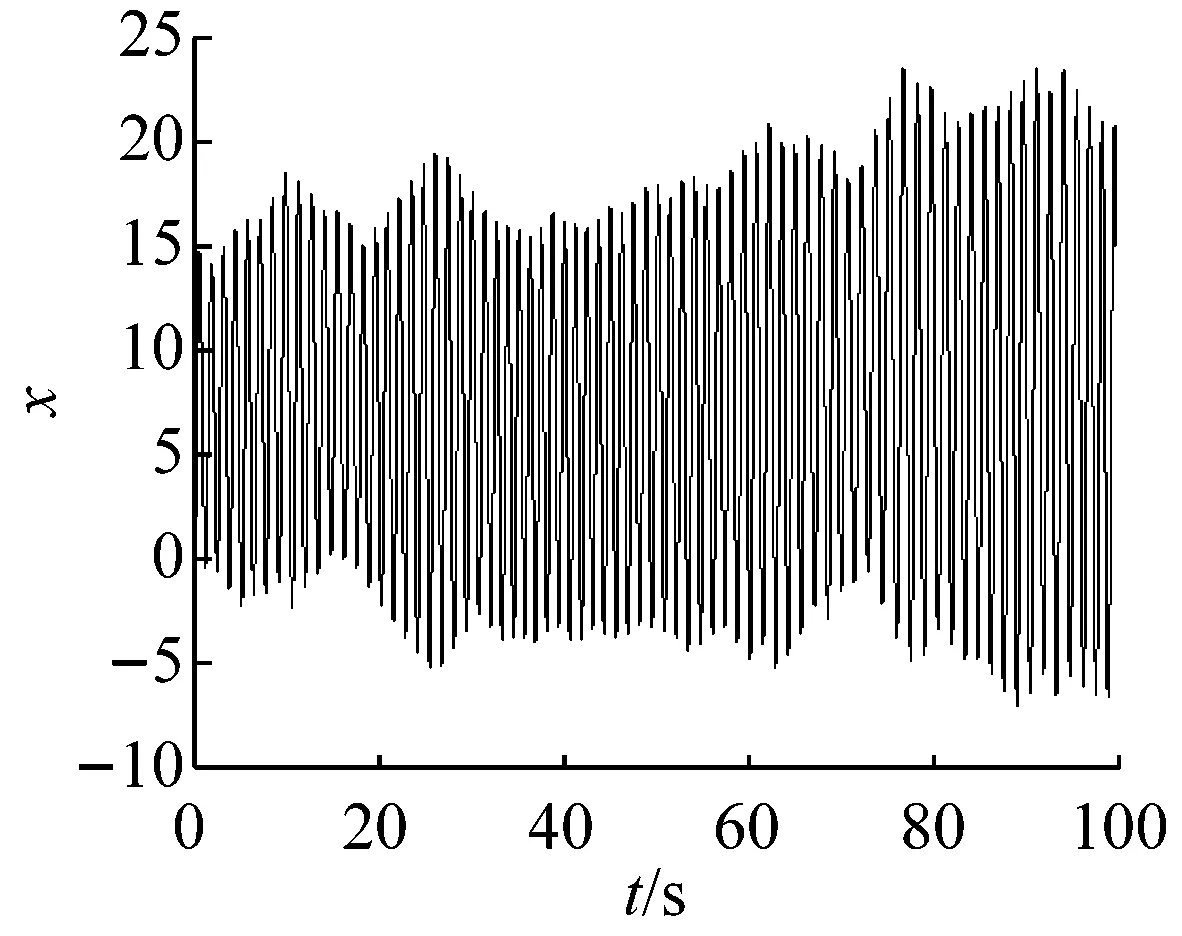
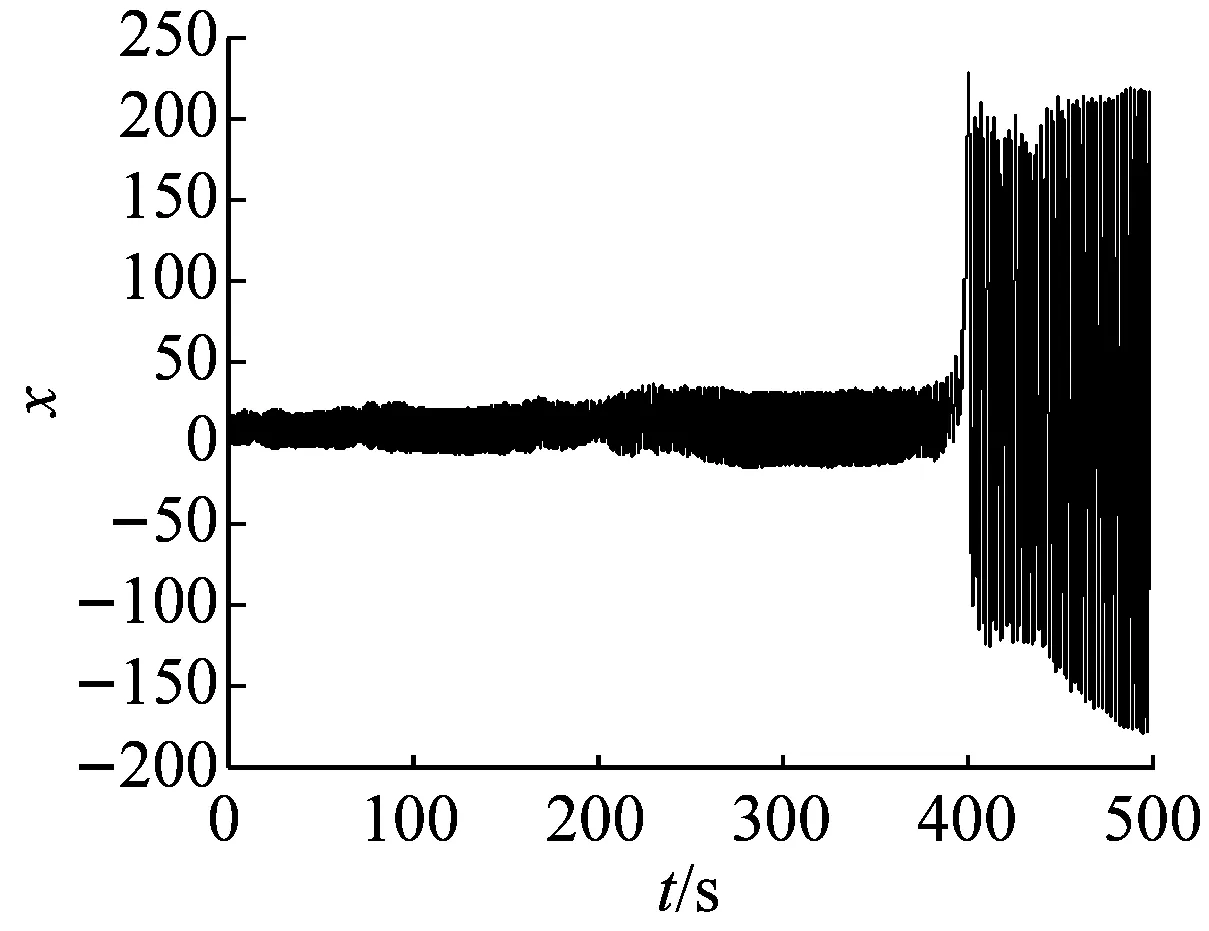
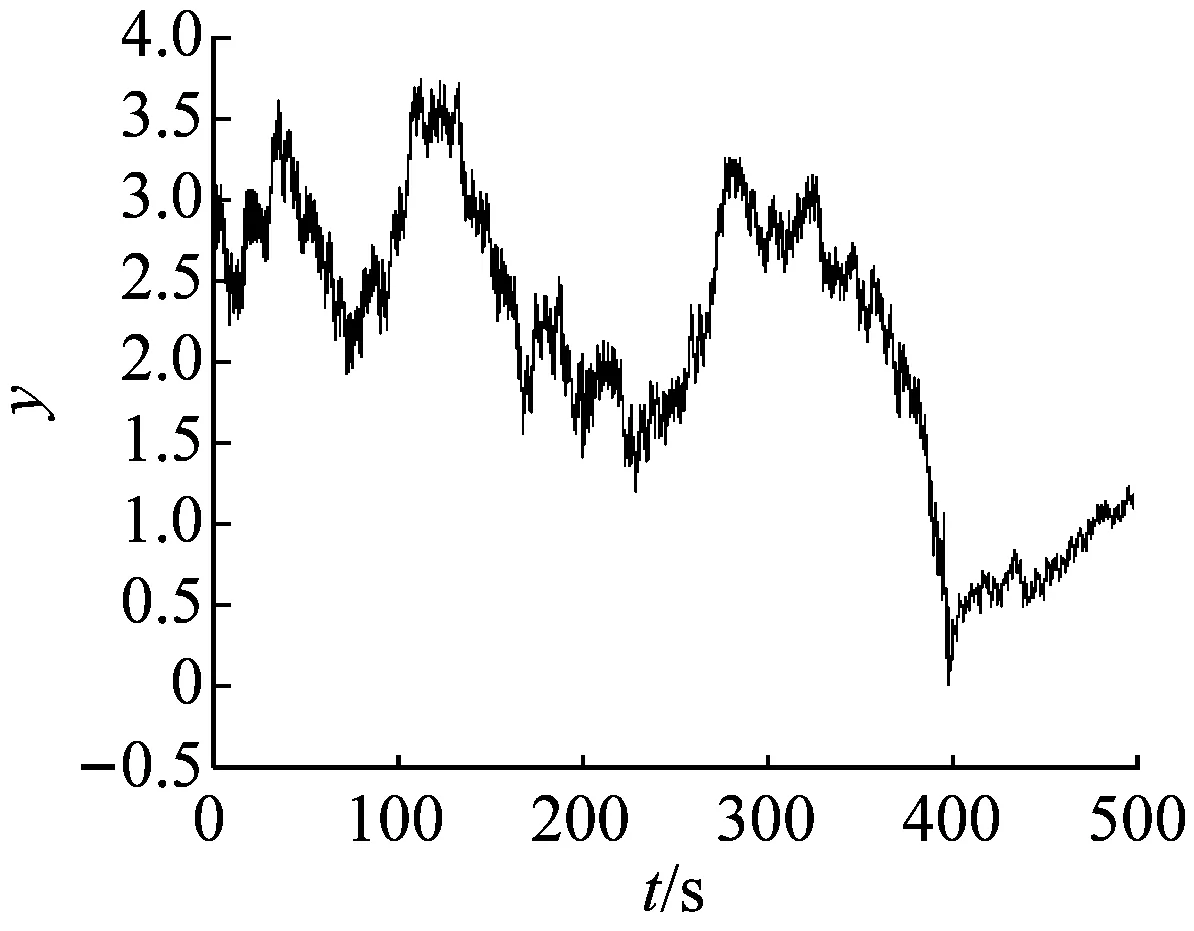
当参数a=8,b=3,c=8,d=20,初始状态(x0,y0,z0)=(-1,3,-1)和仿真时间t1=100 s时,由图2所示,很容易估计出系统状态x和z的混沌时间序列的范围:
x∈(-10,25),z∈(-10,10)
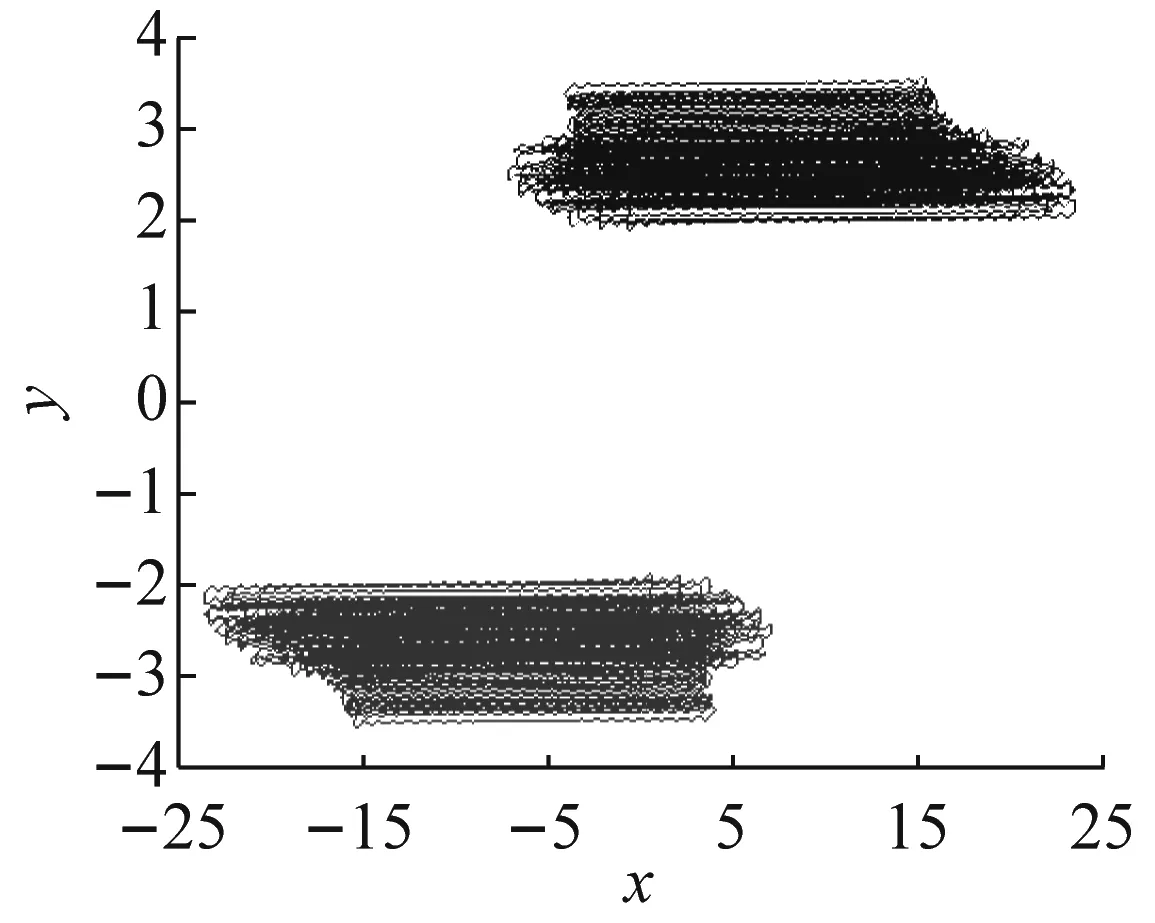
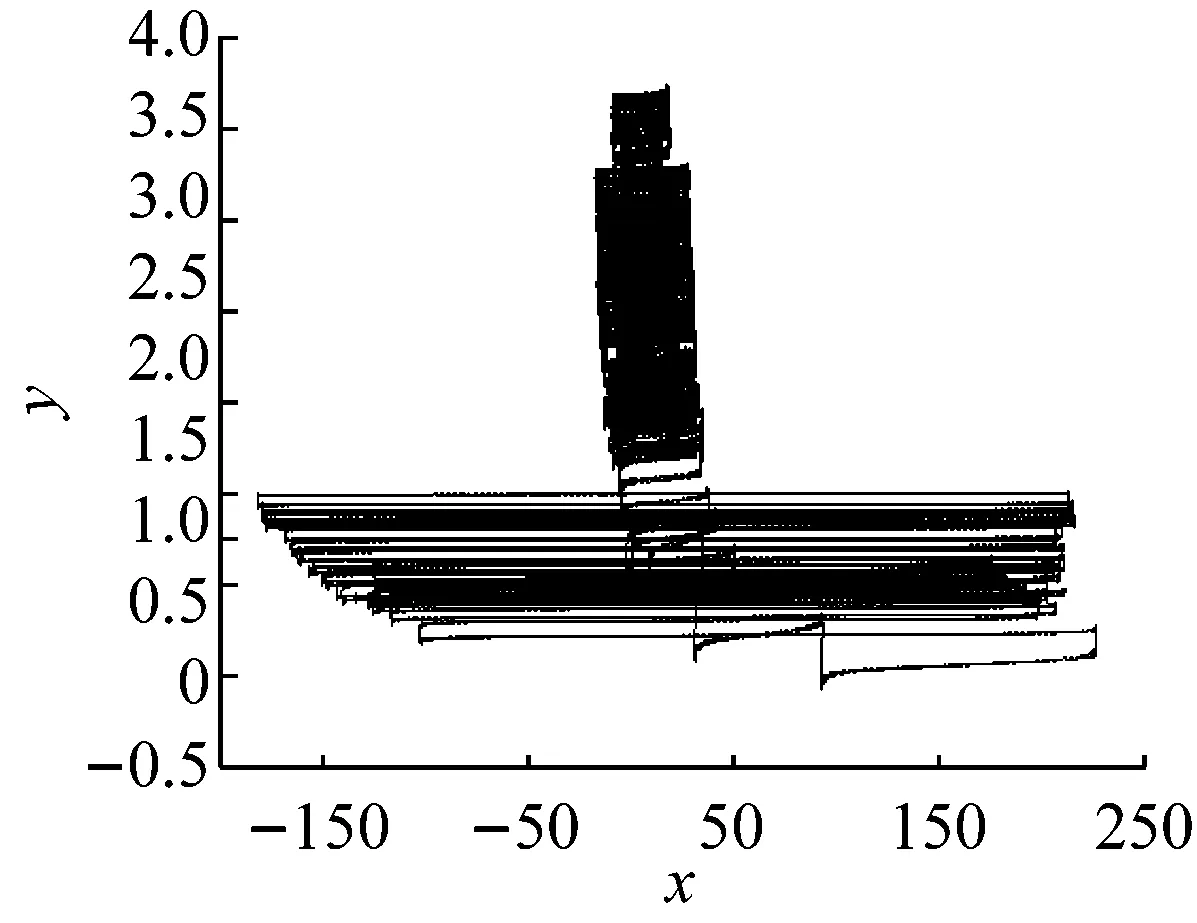
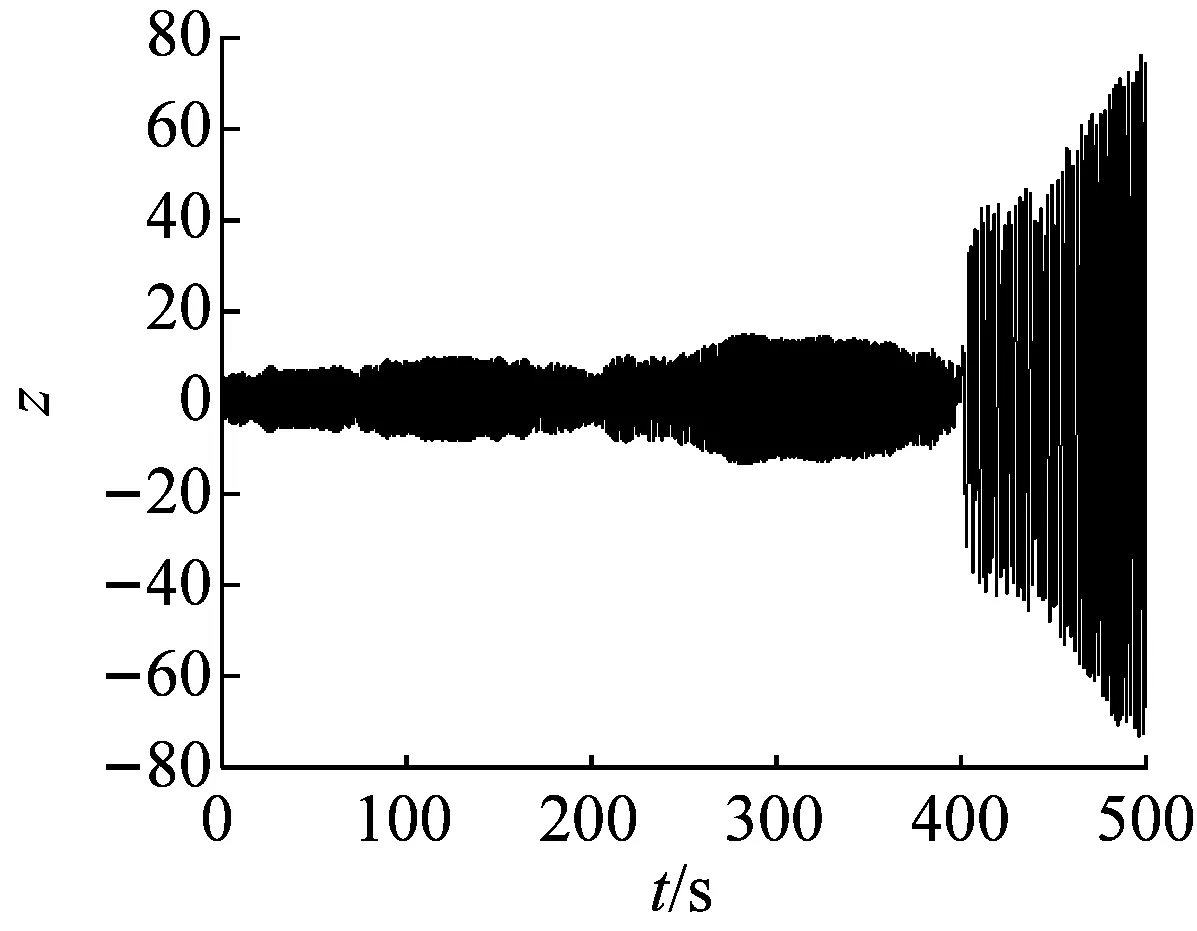
当取相同的参数和初始状态时,进一步延长仿真时间,增加至t2=500 s。系统状态的运行轨道突然出现了大幅度的跃迁现象(如图4所示),相应的混沌时间序列如图5所示。
(a)

(b)

(c)
(a)
(b)
(c)

(a)

(b)
(c)
在系统状态的运行轨道突然出现大幅度跃迁的同时,通过对图5的观测分析,在时间t接近400 s时,系统状态x和z的振动幅度也相应的突然剧烈增加,相应的混沌时间序列范围变为:
x∈(-200,250),z∈(-80,80)
由于这类大幅度混沌振动的突然出现,可能导致实际工程系统瞬间失稳,那么如何对这类系统实现有效地快速控制,下面将采用单参数调控方法,来消除大幅度的混沌振动。
3 新混沌系统的单参数振动控制
在不改变系统平衡点的数量和空间位置的条件下,来实现对混沌系统的控制。在系统式(1)的第三个方程引入线性状态反馈u=mz,得到受控的混沌系统如下:

(9)
(a)
(b)
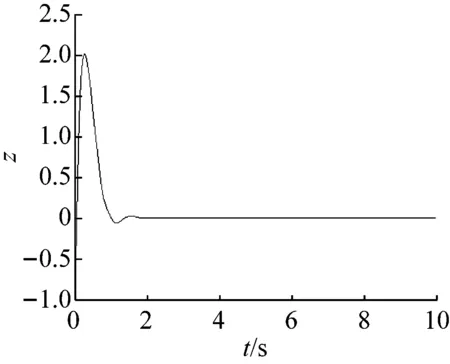
(c)
通过调节控制参数m,分别控制系统到不同的平衡点E(x*,y*,0),其中:x*y*=d。
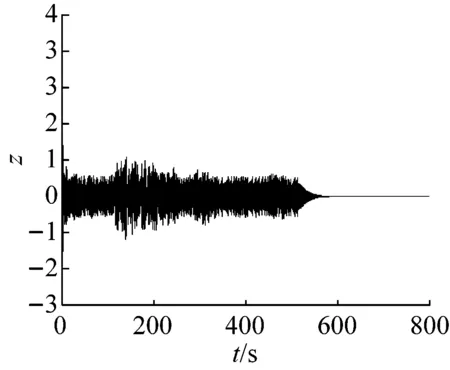
当参数a=8,b=3,c=8,d=20,初始状态(x0,y0,z0)=(-1,3,-1),系统式(1)处于混沌状态(如图1所示)。取参数m=-1,仿真时间t3=800 s时,受控的混沌系统(9)在经历暂态混沌(持续时间大约500 s)之后到达一个平衡点E1(x1,y1,0)(如图6所示),其中:x1y1=d=20。
当参数m≤-1时,每次选取不同的参数值m,系统状态将分别被控制到不同的平衡点E(x*,y*,0),均满足x*y*=d。而且,参数值m取值越小,系统收敛到平衡点E(x*,y*,0)的速度越快,即:可以实现在有限时间内对混沌的有效控制。
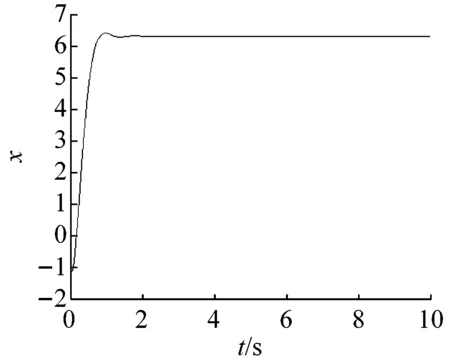
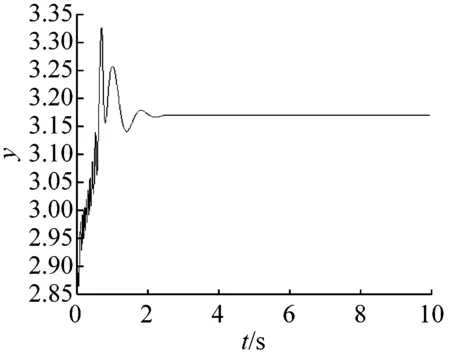
例如:当参数m=-8时,受控的混沌系统式(9)不经历暂态混沌,将在很短的时间(大约3 s)内收敛到另一个平衡点E2(x2,y2,0)(如图7所示),其中:x2y2=d=20。
4 结 论
本文提出了一个具有无穷多个平衡点和隐藏吸引子的新混沌系统,对其动力学行为展开了理论分析。系统的全部平衡点均落在一个平面的双曲线上。在状态和参数的组合变换下,对称的隐藏吸引子是共存的。在双参数对称变换下,混沌具有不变性。状态轨道出现了大幅度的跃迁,混沌振动的振幅也随之剧烈增加。同时,在不改变系统平衡点数量和位置的情况下,设计出了具有单参数调节功能的线性状态反馈控制器,在有限时间内,保证系统状态到达平衡点,进而有效消除混沌振动。针对此类特殊系统的研究,对如何有效预防和解决实际工程中出现的突发大幅度混沌振动问题,在理论基础和控制方法上,提供了良好的借鉴和启示。
[1] LIU Yongjian, YANG Qigui. Dynamics of a new Lorenz-like chaotic system [J]. Nonlinear Analysis: Real World Applications, 2010, 11(4): 2563-2572.
[2] WANG Xiong, CHEN Guanrong. A gallery of Lorenz-like and Chen-like attractors [J]. International Journal of Bifurcation and Chaos, 2013, 23(4): 1330011
[3] WANG Xiong, CHEN Guanrong. Constructing a chaotic system with any number of equilibria [J]. Nonlinear Dynamics, 2013, 71(3): 429-436.
[4] LI Chunbiao, SPROTT J C. Chaotic flows with a single nonquadratic term [J]. Physics Letters A, 2014, 378(3): 178-183.
[5] SUN Changchun. Generation of countless embedded trumpet-shaped chaotic attractors in two opposite directions from a new three-dimensional system with no equilibrium point [J]. Chinese Physics B, 2014, 23(9): 090502.
[6] SUN Changchun, ZHAO Enliang, XU Qicheng. Generation of a novel spherical chaotic attractor from a new three-dimensional system [J]. Chinese Physics B, 2014, 23(5): 050505.
[7] LEONOV G A, KUZNETSOV N V. Hidden attractors in dynamical systems from hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits [J]. International Journal of Bifurcation and Chaos, 2013, 23(1): 1330002.
[8] LEONOV G A, KUZNETSOV N V, VAGAITSEV V I. Hidden attractor in smooth Chua systems [J]. Physica D, 2012, 241(18): 1482-1486.
[9] 陈予恕. 非线性振动系统的分叉和混沌理论 [M].北京:高等教育出版社,1993.
[10] 霍冰,刘习军,张素侠,等. 覆冰导线非线性舞动系统的奇异性和混沌分析 [J]. 振动与冲击, 2015,34(13): 36-41.
HUO Bing, LIU Xijun, ZHANG Suxia, et al. Singularity and chaos of nonlinear galloping for an iced transmission line [J]. Journal of Vibration and Shock, 2015, 34(13): 36-41.
[11] 张伟,姚明辉,张君华,等. 高维非线性系统的全局分岔和混沌动力学研究 [J]. 力学进展,2013, 43(1): 63-90.
ZHANG Wei, YAO Minghui, ZHANG Junhua, et al. Study of global bifurcations and chaotic dynamics for high-dimensional nonlinear systems [J]. Advances in Mechanics, 2013, 43(1): 63-90.
[12] 孙常春,方勃,黄文虎. 基于线性状态反馈的混沌系统全局控制 [J]. 物理学报,2011, 60(11): 110503.
SUN Changchun, FANG Bo, HUANG Wenhu. Global control of chaotic systems based on linear state feedback [J]. Acta Physica Sinica, 2011, 60(11): 110503.
[13] 王林泽,高艳峰,李子鸣. 基于新蝶状模型的混沌控制及其应用研究 [J]. 控制理论与应用,2012, 29(7): 915-920.
WANG Linze, GAO Yanfeng, LI Ziming. Chaos control and its application based on novel butterfly-shaped model [J]. Control Theory & Applications, 2012, 29(7): 915-920.
[14] ZHOU Wuneng, PAN Lin, LI Zhong, et al. Non-linear feedback control of a novel chaotic system [J]. International Journal of Control, Automation, and Systems, 2009, 7(6): 939-944.
[15] ZHANG Jianxiong, TANG Wansheng. Control and synchronization for a class of new chaotic systems via linear feedback [J]. Nonlinear Dynamics, 2009, 58(4): 675-686.
Dynamicalanalysisandvibrationcontrolofanovelchaoticsystemwithinfiniteequilibria
SUNChangchun1,CHENZhongtang1,HOUXianglin2
(1. School of Science, Shenyang Jianzhu University, Shenyang 110168, China; 2. School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168, China)
A novel three-dimensional chaotic system was presented. Its strange dynamical behaviors were investigated by theoretical analysis and numerical simulations. The system has infinite equilibria locating on a hyperbola in a plane. Symmetric hidden attractors can be generated via a combinational transformation on states and parameters. The chaos is invariant under a double-parameter symmetric transformation. Simultaneously, a larger orbital transition phenomenon appears. Finally, a linear state feedback controller with an adjustable parameter was designed to eliminate the chaos within a finite time.
new chaotic system; infinite equilibria; hidden attractor; dynamical analysis; vibration control
TP273; O322
A
10.13465/j.cnki.jvs.2017.21.032
辽宁省自然科学基金(2015020129;2016010624);辽宁省教育厅科学技术研究项目(L2013229);沈阳建筑大学学科培育项目(XKPY-2015-02);沈阳建筑大学学科涵育项目(XKHY-78;XKHY2-103);沈阳建筑大学科学研究项目(2017047)
2016-04-01 修改稿收到日期:2016-04-09
孙常春 男,博士,副教授,1979年生

