Dirac光子晶体∗

王海啸 徐林 蒋建华2)

1)(苏州大学物理与光电.能源学部,苏州 215006)2)(苏州大学,2011苏州纳米科技协同创新中心,苏州 215006)

Dirac光子晶体∗

王海啸1)†徐林1)蒋建华1)2)‡

1)(苏州大学物理与光电.能源学部,苏州 215006)2)(苏州大学,2011苏州纳米科技协同创新中心,苏州 215006)

(2017年8月15日收到;2017年10月31日收到修改稿)

Dirac费米子作为粒子物理中的基本粒子之一,其理论在近年来蓬勃发展的拓扑电子理论领域中被广泛提及并用来刻画具有Dirac费米子性质的电子态.这种特殊的能态通常被称为Dirac点,在能谱上表现为两条不同能带之间的线性交叉点.由于Dirac点往往是发生拓扑相变的转变点,因而也被视为实现各种拓扑态的重要母态.作为可与拓扑电子体系类比的拓扑光子晶体因其独特的潜在应用价值也受到人们的广泛关注,实现包含Dirac点的光子能带已成为研究拓扑光子晶体的核心课题.本文基于电子的拓扑理论,简要地回顾了Dirac点在光子系统中的研究进展,特别介绍了如何在光子晶体中利用不同晶格对称性实现在高对称点/线上的Dirac点,以及由Dirac点衍生的Weyl点.

光子晶体,Dirac点,拓扑能带,量子自旋霍尔效应

1 引 言

1928年,Dirac[1]给出了自旋为1/2的粒子在相对论量子力学下的波动方程,方程的解代表着一类基本粒子,称为Dirac费米子(包含电子和正电子).特别地,当粒子的质量为零时,粒子的能量与动量呈现出线性关系.通常人们将具有这种线性色散关系的粒子称为无质量Dirac费米子.在凝聚态物理中,无质量Dirac费米子的色散关系也用于描述某些特殊的电子态,这些电子态被称为Dirac点.其中最为人们所熟悉的就是石墨烯,它的能带结构在布里渊区边界K(K′)处具有线性色散关系[2].这种电子态具有一些非常奇特的传输性质,例如室温量子霍尔效应[3]和Klein隧穿[4]等.

近年来拓扑电子理论在凝聚态领域的迅速发展使得Dirac方程又重新焕发出活力,系统的研究表明Dirac方程对理解拓扑绝缘体和拓扑超导体的性质和相变具有重要意义[5].人们发现,在连续变化下只要能带之间的带隙不闭合,那么系统的拓扑性质就不会发生改变.换言之,能带拓扑性质的改变总是需要经历能带闭合-打开的过程.Dirac点作为能带的线性交叉点,是能带闭合-打开的转变点,无疑在拓扑能带理论中占据着举足轻重的地位.历史上,Dirac点是获得非平庸拓扑能带的一个重要途径.早在1988年,普林斯顿大学的霍尔丹(F.D.M.Haldane)首次在六角蜂窝晶格中给出了量子反常霍尔效应(quantum anomalous Hall e ff ect)的玩具模型[6].这个模型可以无需借助外磁场而实现具有非平庸陈数的拓扑能带,其性质类似于外磁场为零的量子霍尔效应,对应系统的边界上有一个单向传输的边界态出现.在Haldane模型中,从平庸能带到非平庸能带的转变就是通过打开蜂窝晶格中Dirac点的能隙实现的.需要说明的是,在Haldane模型中只有两种打开Dirac点能隙的方式:第一种方式是破缺空间反映对称性,它导致一个平庸的能带;第二种方式是破缺时间反演对称性,它导致一个拓扑非平庸的能带.

然而,Haldane模型并未考虑电子的自旋.直到2005年,宾夕法尼亚大学的凯恩(C.L.Kane)和米尔(E.J.Mele)在石墨烯系统中发现把Haldane模型扩展到包含电子自旋自由度后,系统可以出现新的拓扑相,称之为Z2拓扑相[7,8].这种特殊的拓扑相并不破缺时间反演对称性,却在系统边界上也存在着一对传播方向相反,自旋极化相反的边界态.由于时间反演对称性的保护,它们能相互稳定共存,即使在无序系统中它们仍然能够保持单向传输且不发生背向散射.这是另一个打开Dirac点的能隙之后导致非平庸的拓扑能带的例子.此后,人们又发现三维的拓扑绝缘体也可以通过打开三维Dirac点的能隙来实现[9].

由以上这些例子可见,在Dirac方程中引入非零质量项而打开Dirac点能隙,可以使系统发生拓扑相变.那么,如果不打开Dirac点的能隙能否实现系统的拓扑相变呢？答案是肯定的.早在Dirac方程被提出的第二年,Weyl就指出Dirac方程无质量的解描述的是一对新粒子,这一对新粒子具有相反的手性,也就是今天人们常说的Weyl费米子[10].所以,具有四重简并(包含自旋和轨道两个自由度)的Dirac点也可以看成是一对具有相反手性的Weyl点组合而成;而当系统不再具有某种对称性时,手性相反的Weyl费米子的能谱将不再重叠,Dirac点也就会退化成为一对手性相反的Weyl点.

由此可见,无论是拓扑绝缘体,还是近来广受关注的Weyl拓扑节点,都可以通过Dirac点来实现,因此,Dirac点作为拓扑态的一个母态,对于研究拓扑物质态和拓扑相变具有极其重要的意义.

Dirac点在电子系统中的广泛研究也吸引了光学领域研究人员的注意[11−20].因为从能带图像和布洛赫定理来看,光子晶体和原子晶体具有很多的相似性.然而需要指出的是,电子作为费米子具有自旋1/2的独特内禀属性.由于此独特的性质,Kramers定理导致电子在时间反演对称的波矢下具有天然的二重简并,而光子作为玻色子则不具有这样的二重简并.事实上,实现光子拓扑态的核心挑战之一就是要实现光子能带的二重简并.

为此,人们首先根据光特有的偏振特性,利用TE+TM/TE-TM(TE和TM分别表示横向电场和横向磁场模式)[14]混合模式、TM/TE模式[15],左旋光/右旋光[16]等在光学系统中实现了特殊材料/超材料中的二重简并,并借助光子晶体实现了光学系统中的Dirac点和拓扑物质态.我们把利用光学系统的偏振自由度实现二重简的拓扑光子系统以及实现具有陈数的光子系统的研究[12,13]称为拓扑光子学研究的第一阶段.由于这些研究往往需要具有特殊性质的材料,如磁光材料、具有磁电耦合的材料,具有电磁对偶对称性的材料等,而难以有广阔的应用前景.从2015年开始,人们开始提出各种具有特别晶格对称性的光子晶体[18−22],这些光子晶体并不需要特殊的材料,只用普通的介质材料即可实现光子的拓扑态.与以往利用光偏振特性的研究不同,利用晶格对称性可以有效地实现光子能谱在特殊波矢上的二重简并,并进而实现光子的Dirac点.通过打开Dirac点可以实现特殊的拓扑光子态.本文着重介绍基于点群和非点群的对称性来实现光子晶体中的Dirac点和拓扑光子态的方法,首先讨论二维的光子晶体,再扩展到三维的光子晶体.

在开始之前,需要先澄清用词方面的一些混淆.本文中的Dirac点是具有四重简并的线性能谱交叉点.因为Dirac的原始论文考虑的正是一个具有四重自由度的系统:正电子有两重自由度(自旋1/2),电子也有两重自由度,一共有四重自由度.与此相对的,Weyl点指的是具有两重简并的线性交叉点(也可以是抛物线交叉点,这里暂不考虑).在二维系统中,由于无法定义Weyl点,称所有的线性色散交叉点为Dirac点.若二维系统具有四重简并的Dirac点,那么就称之为双Dirac点.

2 二维Dirac光子态

2.1 双Dirac点及相图

理论上最早给出二维介质光子晶体拓扑绝缘体的是日本国家材料科学研究所(NIMS)的Hu研究组[18],他们在蜂窝点阵结构中,通过能带折叠的方式将K和K′点的Dirac点折叠到布里渊区中心,获得了双Dirac点.通过变形点阵结构可以打开双Dirac点的带隙,并实现能带反转,由此实现光子的量子自旋霍尔效应.这里双Dirac点出现的条件是晶格具有C6旋转对称性.因为在二维点群中,只有具有C6对称性的三角晶格系统才会在布里渊区中心出现双Dirac点[23,24].

图1 自然界中广泛存在的核壳结构 (a)海鼠;(b)海鼠体表刺的透射电子显像;(c)海鼠体表的刺;(d)蛋白石头;(e)蛋白石胶体晶体的扫描电子显像Fig.1.Hexagonal photonic crystals in nature:(a)The sea mouse(Aphroditidae);(b)the transmission electron micrograph of the sea mouse spine;(c)images of a sea mouse spine illuminated with light;(d)opal;(e)the SEM images of the colloidal crystal in opal.

2016年,Xu等[20]利用核-壳结构的二维光子晶体给出了另一种实现光子的量子自旋霍尔效应的例子.核-壳结构构成的三角晶格广泛存在于自然界中,包括胶体晶体及海鼠皮肤表面凸起的晶格结构[25,26],都是这种结构(图1).

为方便表述二维核-壳结构光子晶体的拓扑相变机理,在这里核-壳的内径和外径分别设为R1和R2,晶格常数为a=1,核壳结构及背景材料的介电常数分别为ε1=1和ε2=12(见图2(a)插图).利用基于有限元计算方法的COMSOL软件可以计算二维光子晶体的能带结构及其场图,不同宇称能带之间的偶然简并则可以通过调节核壳结构的内外径来实现.特别地,当结构参数R2/R1=0.26/0.45时,在Γ点出现了p带和d带的四重简并态,就是系统发生拓扑转变的双Dirac点(图2(b)).具体而言,奇宇称的两个简并态是两个p波,如px和py态;而偶宇称的两个简并态是两个d波,如dx2−y2和dxy态.一个更好的表象是把它们重新组合成如下的形式:奇宇称的两个态p+=px+ipy和p−=px−ipy,二者可以通过时间反演对称操作相互联系,类比电子系统中的自旋上和自旋下的两个简并态,将其称为p带的赝自旋.类似地,偶宇称的两个态可以表示d+=dx2−y2+idxy及d−=dx2−y2− idxy,分别对应d带的赝自旋上态和赝自旋下态[18].

由于Z2拓扑相是打开双Dirac点得到的,所以我们有必要采用电子能带论发展起来的k·p理论来讨论这些能带之间(p带和d带)的相互作用(k·p理论在Maxwell方程中的正确应用及其对量子自旋霍尔效应的解释请参考文献[20]).首先,TM模式下的Maxwell方程可以写成:

这里的n是光子的能带指标,hn,k(r)是光子磁场的布洛赫函数,它的归一化表达式是

积分区域u.c.代表的是一个原胞单元.(1)式中的厄密算符可以作为光子系统的哈密顿量(目前有一些论文在k·p方法中使用的光子“哈密顿量”不是厄密算符,正确的k·p方法见文献[20]),将布洛赫函数hn,k(r)在Γ点展开,可以得到系统的k·p哈密顿量:

这里的ωn,0表示第n条能带在Γ点的本征频率,动量P矩阵元的表达式为

图2 核-壳结构的能带图及拓扑相变示意图 (a)R2/R1=0.2/0.45,正常的光子绝缘态;(b)R2/R1=0.26/0.45,Dirac光子态;(b)R2/R1=0.3/0.45,量子自旋光子霍尔态;(d)相变示意图,左侧为能带图(a)的第2,3与4,5条能带在Γ点的电场场图,右侧为能带图(c)的第2,3与4,5条能带在Γ点的电场场图Fig.2.The band structure of core-shell photonic crystal and the schematic of topological phase diagram:(a)R2/R1=0.2/0.45,normal photonic insulator state;(b)R2/R1=0.26/0.45,Dirac photonic state;(c)R2/R1=0.3/0.45,quantum spin hall state;(d)schematic of topological phase transfer diagram,left panel is electric field pattern of the 2nd,3rdand 4th,5thband at Γ point in(a);right panel is electric field pattern of the 2nd,3rdand 4th,5thband at Γ point in(c).

注意到只有当第n和第n′条能带的宇称不同时,动量P的矩阵元才不等于零.根据k·p理论,有效哈密顿量在(p+,d+,p−,d−)T表象下的形式是:

式中的k±=kx±iky,A是不同态之间的耦合系数;显然,只有相同的自旋极化方向的p态(d态)之间(即p+与p−,d+与d−)才会有耦合.需要指出的是,(4)式给出的哈密顿量与电子系统中Bernevig-Hughes-Zhang(BHZ)模型[27]给出的哈密顿量相似,其中的两个方块子矩阵分别对应赝自旋上和赝自旋下的有质量的Dirac方程.这一对赝自旋光子对是由时间反演对称操作来联系的,这保证了整个系统仍然满足时间反演对称性.所以,若把p带作为价带,d带作为导带,那么类比电子系统中的BHZ模型,对应的(4)式就可以描述光子的量子自旋霍尔效应:当ωp＜ωd时系统对应的就是拓扑平庸态;当ωp＞ωd时,系统在Γ点处发生了pd宇称反转,这就直接导致了光子的Z2拓扑态;当ωp=ωd=ω0时,在Γ点就会出现一个四重简并点,对应于双Dirac点,即拓扑相变点.

虽然增加或者减小R2/R1的比值时均会打开p带和d带之间的能隙,但根据以上的理论模型分析,有一种类型的能隙是平庸的,另一种类型的能隙则是拓扑的,其关键的点就是看系统是否发生宇称反转(p-d反转).如图2(d)所示,当R2/R1＜0.25/0.46,p带的频率较低(ωp＜ωd),系统对应于普通光子绝缘体;当R2/R1＞0.25/0.46时,d带的频率较低(ωp＞ωd),对应光子拓扑绝缘体.

图3 核-壳结构的相图 (a)p-d反转导致的光子Z2拓扑绝缘体在R1-R2参数空间的相图,对角线以上及以下分别表示正结构及反结构;橙色区域表示p-d正常,对应于正常光子绝缘态,蓝色区域表示p-d反转,对应量子自旋霍尔态,橙色实线表示p-d四重简并态,即双Dirac点;(b)固定外径R1=0.45a,出现双Dirac点对应的介电常数的比率ln(ε1/ε2)与内径R2的关系Fig.3.Phase diagram of core-shell structure:(a)Phase diagram of the p-d inversion-induced photonic Z2topological insulator in the R1-R2parameter space,the diagonal line represents the homogenous limit which separates the normal and reversed structures in the upper and lower triangular regions,the orange region represents that the p bands are lower than the d band at Γ point,whereas the blue region stands for the photonic analog of the Z2topological insulators with the p bands above the d bands at Γ point,the p-d band degeneracy at the Γ point is labeled by black line;(b)relationship between ln(ε1/ε2)and the critical inner radius R2 where the double Dirac cone emerges,the outer radius of the hollow cylinder is fixed at R1=0.45a.

考虑到可以通过结构参数实现光子能带的反转,为使结果更具有普遍性,我们也讨论了R1和R2独立改变对能带反转的影响,得到了能带反转的相图(图3(a)),图中蓝色区域表示p-d反转,橙色区域表示p-d正常.由此可见,二维三角晶格的拓扑相变在很大的参数范围内具有可调性,甚至在反结构(这里定义ε1和ε2交换的结构为反结构,即ε1=12＞ε2=1)中也能实现能带宇称的反转.同时,我们还讨论了ε1和ε2的比值对双Dirac点出现时的几何参数R1和R2的影响(图3(b)).通常情况下,光子晶体的能隙会随着不同介质的介电常数比值的增加而增加;但有意思的是,当固定外径R1(=0.45a)调节内径R2及ε1/ε2以获得双Dirac点时,我们发现内径的临界值在ε1/ε2很大的一段范围变化很小,这说明对介电常数对双Dirac点的影响远小于几何参数.

需要注意的是,这里的物理和文献[18]中考虑的蜂窝晶格很不一样,蜂窝晶格一定会出现双Dirac点,可以把这种对称性导致的双Dirac点称之为必然简并点.然而,核-壳结构中双Dirac点的出现具有一定的偶然性,不受简单因素的决定.对于二维核壳光子晶体,可以认为每个核壳都是一个共振腔,其中的局域态可以认为是Mie散射造成准局域态[28].该光子晶体中的光子能带可以看成是相邻格点中的准局域态之间的相互耦合／杂化导致的.通过调节球壳结构的内径和外径,可以有效地调节p态和d态的能量和场分布,由此有效地调节p带和d带的能量,从而实现宇称反转的拓扑光子态.

2.2 边界态及赝自旋选择的单向传输

现在我们来讨论光子拓扑绝缘体的边界态性质.在上述核-壳系统中,我们可以选取两种能隙匹配且具有不同拓扑性质的光子晶体实现具有拓扑保护的边界态,它的Z2拓扑相受到了赝时间反演对称性的保护,该赝时间反演对称算符可以表示成Tp=iσyK(K表示复共轭算符),其中的σy项可以写成C6对称操作的线性组合使得T2p=−1.这里需要说明的是,只要系统具有二重简并态,我们总是可以构造出这种反幺正算符.因此,若要在光子晶体中模拟Z2的拓扑,关键就是要找到两种不同宇称的双重简并态.在这里,我们选取两种尺寸相近、拓扑性质不同的光子晶体(Z2=0与Z2=1)来产生边界态(图4(a)与图4(b)).

从图4可以看到,A点对应边界态的场图的坡印廷矢量方向是顺时针,代表自旋上;B点对应边界态场图的坡印廷矢量方向是逆时针,代表自旋下;他们是由时间反演对称性联系的.值得注意的是在图4(c)中,由于Γ点处的p态及d态的二重简并是由点群对称性保护的,而在由不同结构组成的边界明显地破坏了C6的对称性,这使得原本是线性交叉的边界态打开了一个微小的能隙,计算模拟表明这个打开的能隙与边界破坏C6对称性的程度有密切的关系.虽然表面态打开了一个小的能隙,然而这些光子晶体体能带的拓扑性质是没有歧义的(虽然目前的理论还没有严格证明这一点,我们最新的基于Berry phase的计算已经证明了非平庸的拓扑数).

图4 拓扑边界态 (a)p-d正常态的能带结构,R1=0.4a,R2=0.26a;(b)p-d反转态的能带结构,R1=0.45a,R2=0.32a,共同能隙由青色的区域标出;(c)两种不同光子晶体构成的投影能带;(d)A点对应边界处的电场分布,对应的坡印廷矢量方向为顺时针,代表自旋向上;(e)B点对应边界处的电场分布,对应的坡印廷矢量方向为逆时针,代表自旋向下Fig.4.Topology-induced edge states:(a)The normal band structure with R1=0.4a and R2=0.26a;(b)the normal band structure with R1=0.45a and R2=0.32a,the common complete band gap is marked with the cyan ribbon;(c)the projected band structure of two photonic crystals with oblique line edge,A and B mostly comprise of the pseudo-spin-up and spin-down edge states,respectively;(d)and(e)are the Ez field pattern of A and B.

3 三维Dirac光子态

3.1 受点群对称性保护的三维第一类Dirac光子态

在二维情况下,我们利用点群对称性制造光子的自旋自由度,成功地实现光子的量子自旋霍尔效应,那么有没有可能将上述结果推广到三维系统中呢？答案是肯定的.因着真正的材料总是三维,在三维光子系统中实现Dirac点具有重要的现实意义.然而,若要类比电子系统在光子晶体实现三维Dirac点至少有两个问题亟待解决:1)电子与光子两种粒子的性质不同,光子是玻色子,缺少自旋自由度;2)光子能带形成的机理与电子也不同,电子能带可以被认为是不同局域原子轨道混合的结果,光子能带是由多重布拉格散射造成的结果,缺少局域轨道自由度的图像.

为此,我们在二维核-壳结构的基础上,提出了由两个中空介质柱组成结构单位,构成三维六角晶格光子晶体(图5(a)和(b)).根据文献[28],光子系统中的Mie散射共振看作是光子的局域轨道,不同的光子能态可以看作是不同波之间的Mie散射共振.这里将中空柱子的Mie散射共振看作是光子的局域轨道;那么,类比二维的情况,光子的p带和d带就可以被认为是来自p波和d波的Mie散射共振.需要再次强调的是,只有C6v对称群包含两个二重简并的表象,并且这两个二重表象具有相反的宇称.根据宇称的选择定则,两个宇称相反的态之间的相互作用必定导致线性色散.因此,对三维情况而言,只有在动量空间满足六重旋转对称操作的不变高对称线上,才可能出现稳定的Dirac点.事实上,我们发现在ΓA这条高对称线上p带及d带是二重简并的(图5(c)),这与上述的判断是一致的.不仅如此,理论计算也发现三维Dirac点总是出现在ΓA或KH这条线上;甚至移除两个中空圆柱之间的六根柱子后,在ΓA或KH这条线上的Dirac点也是存在的.这是因为在六角晶格中ΓA和KH都是动量空间中满足六重旋转不变的高对称线.需要特别指出的是,光子晶体中的这种性质与电子系统具有巨大的差异:在电子系统中,具有C3,C4和C6对称操作的结构都可以出现稳定的Dirac点[29].由于在布里渊区高对称点处的四重简并态总是不稳定的,C6点群对称性的引入使得Dirac点变得相当的稳定.

为证明以上的判断,我们仿照二维的例子,选取(d+,p+,d−,p−)T作为系统k·p哈密顿量的基矢量. 首先,根据|px〉,|py〉,|dx2−y2〉,|dxy〉波函数的对称性及动量算符Px和Py的作用形式,可以得到

因此,〈p+|H|d+〉=〈p−|H|d−〉∗=A||k||eiθk, 这里θk=Arg[kx+iky]是x-y平面内的幅角,A||=〈px|Px|dx2−y2〉.

图5 点群对称性导致的三维Dirac光子晶体 (a)实空间六角晶格结构光子晶体原胞,中空圆柱及六根柱子均是用相同介质构成;(b)六角晶格结构的俯视图,其中a是xy平面内的晶格常数,a1和a2是晶格的基矢量.高度为h=0.6a,外径和内径分别为Rout=0.5a和Rin=0.45a,高度为0.4a;(c)倒空间中的第一布里渊区,红色及蓝色小球分别代表不同拓扑电荷的Dirac点;(d)六角晶格光子能带;插图为Dirac点三维色散结构;(e)ΓA高对称线上的能带,其中红线代表的p带和=绿线代表的d带在处相交;(f)Γ点p带和d带在xy平面内的场图Fig.5.Three dimensional Dirac photonic crystal induced by point group symmetry:(a)Structure in real-space unit cell of hexagonal photonic crystals,hollow cylinder and micropillars are made of the same material with isotropic permittivity;(b)top-down view of hexagonal photonic crystal,a1and a2are the two lattice vectors in the x-y plane,the height of each unit cell is h=0.6a,the outer and inner radii of the hollow cylinder are Rout=0.5a and Rin=0.45a,respectively,whereas its height is 0.4a;(c) first Brillouin zone with a pair of Dirac points along the Γ-A line,a Dirac point with di ff erent topological charge is labeled as a red and blue point;(d)photonic band structure of a hexagonal photonic crystal with C6and inversion symmetry,inset is the dispersion of Dirac point with Kz＞0;(e)band structure along line,the p bands(red)cross the d bands(green)at(0,0,Kz)with Kz=0.338;(f)Ez field pro file in the x-y plane of p bands and d bands.

最终,系统在基矢量(d+,p+,d−,p−)T表象下的k·p哈密顿量:

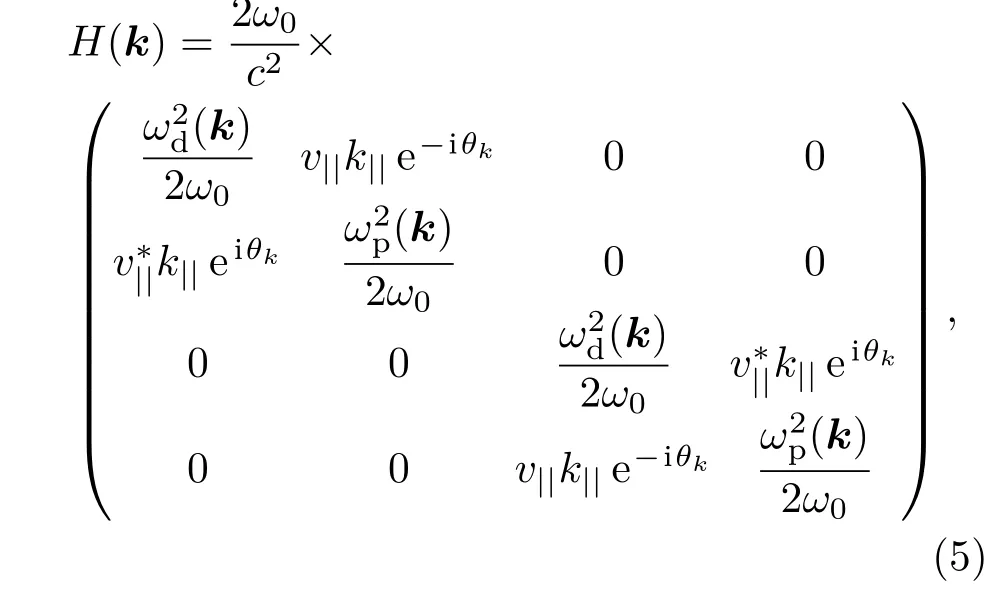
其中ω0表示Dirac点对应的频率,是在x-y平面内的群速度分量,它是kz的函数,可以发现对每一个给定的kz,(5)式都是代表一种拓扑平庸或非平庸的系统:当|kz|＞Kz时,ωp,0(kz)＜ωd,0(kz),在Γ点p态频率比d态频率要低,系统对应的将是拓扑平庸态(普通绝缘体);当|kz|＜Kz时,ωp,0(kz)＞ωd,0(kz),在Γ点p态频率比d态频率要高,系统对应的将是拓扑态;当|kz|=Kz时,ωp,0(kz)=ωd,0(kz),即Dirac点.需要注意的是,虽然这种Dirac点是一种偶然简并导致的四重简并点,其位置Kz是随着结构参数的改变而改变的,但只要p带和d带在Γ点交换频率顺序,这种偶然简并将会是不可避免的.以三维Dirac点作为临界点,在|kz|=Kz的两边将会出现两种不同拓扑性质的绝缘体.由此可见,三维Dirac点是相应二维系统拓扑相变临界点.

3.2 受非点群对称性保护的三维第二类Dirac光子态

通过点群对称性,我们已经得到了相当稳定的三维Dirac点.在这部分,我们将介绍基于非点群对称性引入的三维Dirac点,所谓非点群对称操作包括旋转(或镜面)加上平移(小于晶格常数距离)(图6(a)).作为例子,我们给出了的原胞中都有两个垂直且完全相同的介质块(图6(b)),对应的介电常数εb,背景填充材料的介电常数εm的在三个方向上的晶格常数都为a=1,该结构关键的对称性包括:1)二重旋转对称性Sx:=(x,y,z)→(0.5+x,0.5−y,0.5−z)及Sy:=(x,y,z)→(0.5−x,0.5+y,0.5−z);2)绕着z轴180◦旋转的C2:=(x,y,z)→(−x,−y,z);3)时间反演对称性T:t→−t;4)三个方向的镜面对称性M1:=(x,y,z)→(y,x,z);M2:=(x,y,z)→(−y,−x,z);M3:=(x,y,z)→(y,x,−z).在此,我们采用MIT Photonic Band(MPB)软件包来计算三维光子晶体的能谱,结果显示,能谱在kx=π面上都具有二重简并度(图6(c)),并且在高对称线MA上具有两个四重简并点(Dirac点),对应的光子能态呈现出p态和d态(图6(d)).

为了说明在kx=π(ky=π)面上的二重简并,构造以下反幺正算符:,其中的T是时间反演算符,相当于对光子的布洛赫波函数做复共轭运算;可以发现,就是相当于一个空间平移矢量r=(1,0,0),那么作用两次算符在布洛赫的波函数上,即eikxψnk(r).显然在kx=π的平面上,根据Kramers简并条件,所有在kx=π的平面上的布洛赫态将是二重简并态.类似地,也可以证明,所有在ky=π的平面上的布洛赫态将也是二重简并态.这表明利用非点群对称性也可以增加光子能带的简并度,以此获得光子赝自旋的自由度.

另一方面,实现三维光子晶体Dirac点还要给出宇称反转的图像.在这里通过二重旋转轴C2来定义xy平面内的宇称;注意到两个正交的旋转对称算符满足如下对易关系是:SxSy=T010C2及SxSy=T100C2.因此,在MA这条高对称线上,我们可以得到对易关系式,也就是说在MA这条高对称线上算符与算符和C2对称操作都是对易的.所以,任意两个简并态都会具有相同的C2的本征值c2,而这个本征值c2=±1就可以被我们用来标记xy平面内的宇称.由此,当任意两个在MA线上具有不同宇称的能带的交叉点就是三维的Dirac点,对应Dirac点的拓扑电荷[30]为,这里的表示Dirac点较低频率能带的宇称,k0表示Dirac点所对应波矢.根据图6在最低的六条能带中总共有四个拓扑电荷NDP=±1的Dirac点,他们都是由双重简并的p波及d波的能带线性交叉形成的.

值得说明的是,这种利用非点群对称性引入得的三维Dirac点并不十分依赖于结构单位的形状大小以及介质的参数,任意两种不同宇称的能带交叉点都是Dirac点.由此可见,基于非点群对称的结构设计是一种非常有效的方法来实现三维Dirac点.

图6 非点群对称性导致的三维Dirac光子晶体 (a)非点群操作示意图;(b)左侧为三维结构原胞(边界有黑色实线标注),右侧为两种正交旋转对称操作Sx和Sy的示意图;(c)kx=π光子能带,右侧为高对称线MA上的Dirac点;(d)p带和d带的二重简并的磁场场图;相关参数0.5a,w=0.2a,h=0.5a,材料的介电常数分别是εb=16,εm=1.9;(e)I型Dirac点的三维色散;(f)II型Dirac点的三维色散Fig.6.Three dimensional Dirac photonic crystal induced by non-symmorphic symmetry:(a)Schematic of nonsymmorphic symmetry operation;(b)left is 3D structure of a unit cell(boundaries are indicated by black lines),right is Illustration of the two orthogonal screw symmetries Sxand Syin top-down view;(c)photonic band structure with kx=π,parity inversion on the MA line;(d)left and right are magnetic field pro files of the p and d wave doublet,respectively,parameters0.5a,w=0.2a,h=0.5a,and permittivity εb=16 and εm=1.9;(e)3D dispersion of type-I Dirac point;(f)3D dispersion of type-II Dirac point.

4 三维Weyl光子态

在2013年,麻省理工学院的Lu等[31]在破缺空间反映对称性的螺旋二十四面体光子晶体中发现了Weyl点.然而,在这种依赖于特定结构的Weyl点并不具有普遍性.另一方面,我们知道三维Dirac点可看作是由一对手性相反的Weyl点构成.因此,在破缺系统的某些对称性后,三维Dirac点将会演化为一对手性相反的Weyl点,相应的拓扑不变量也将由Z2数变为陈数.根据这个思路,我们以上述两种受对称性保护的三维Dirac点为例,来阐述如何由Dirac点得到Weyl点.

图7 保持C6对称性且破缺空间反演对称性后的六角晶格光子晶体 (a)原胞结构的侧视图及俯视图;(b)kz方向上的光子能带(忽略其他不相干的能带),存在着两对Weyl点;(c)第一布里渊区内Weyl点的示意图,绿色和黄色小球分别代表手性不同的Weyl点;(d)陈数分布图:红线表示p−-d−的能带,蓝线表示p+-d+的能带;(e)两个Weyl点的附近光子三维色散Fig.7.Inversion symmetry broken hexagonal photonic crystal with C6symmetry:(a)Lateral(left)and top-down(right)views of the structure in a real-space unit cell;(b)photonic bands along the kz-direction,two pairs of Weyl points are found;(c)depicting the four Weyl points in the first Brillouin zone,green(yellow)spheres denote Weyl points with chirality −1(+1);(d)Chern number Ncfor the p+-d+bands below the Weyl points(blue)and for the p−-d−bands below the Weyl points(red);(e)photonic spectrum near the two Weyl points,left for WP at(0,0,Kz1);right for Weyl points at(0,0,Kz2).

4.1 受点群对称性保护的Weyl光子态

对于由点群对称性保护的三维Dirac点,我们知道ΓA高对称线上具有二重简并的p带和d带是由C6及z方向上的反映对称性保护的,因此通过破坏旋转连接两个中空圆柱的六根棍子来破坏系统的空间反映对称性,使得p+带和p−带及d+带和d−带解简并,同时由于系统仍然存在C6的对称性,使得具有不同C6操作本征的四条能带将仍然彼此交叉,所以空间反演对称性的破坏相当于在原来的系统中引入一个质量项.这时,一对Dirac点将会分裂形成四个Weyl点,这时描述系统的拓扑不变量就是陈数,根据图7在0.2＜|kz|＜0.26的范围内,总的陈数是非零的,这种陈数的分布是Z2Dirac点导致的显著特征.这一影响也使得边界态成为单向传输的边界态.

4.2 受非点群对称性保护的Weyl光子态

对于由非点群对称性保护的Dirac点,为了获得Weyl点所需要破缺对称性包括：旋转对称性(Sx及Sy),三个镜面对称性(M1,M2,M3)以及系统的空间反演对称性P,而只保留180◦旋转对称性.显然,破坏了系统的旋转对称性会解除在MA高对称性上的二重简并性;另一方面,180◦旋转对称性仍然保证在MA这条高对称线上不同宇称能带的偶然线性交叉,这种线性交叉就是Weyl点.从图8可以发现总共有三对Weyl点,包括两对II型的Weyl点和一对I型的Weyl点,其中最低频率d带与其他能带交叉导致的Weyl点的三维色散由图8给出.

图8 由Dirac点衍生得到的Weyl点 (a)对称性破缺的原胞结构,上图为原胞结构放大的俯视图,下图为沿[110]方向的侧视图,几何结构参数为b1=0.1,b2=0.11,b3=0.094,h1=0.5,h2=0.3;(b)kz方向上的光子能带图,对应的能带交叉点就是Weyl点;(d)Weyl点的三维色散图,上图为II型的Weyl点,下图为I型的Weyl点Fig.8.Weyl points derived from Dirac points:(a)Unit cell structure of the symmetry-broken,upper panel is 3D view with zoom in illustration of structure deformation,lower panel is side view from[110]direction,the geometry parameters are b1=0.1,b2=0.11,b3=0.094,h1=0.5,and h2=0.3,the z coordinates of the centers of the two types of dielectric blocks are 0 and 0.65a;(b)band structure of MA line for lowest six bands,the crossing points are Weyl points;(c)3D dispersion of Weyl points,upper panel is type-II Weyl point,lower panel is type-I Weyl point.

5 结 论

光子晶体中的Dirac点作为实现各种拓扑态的一种重要母态,对光子拓扑理论的研究具有重要的指导意义,如何在光子晶体中实现Dirac点无疑是光子拓扑理论中的一个核心研究课题.通常人们根据光特有的偏振特性来模拟电子系统中的自旋简并态,然而这种方式往往受限于材料的特殊要求(通常只能在特殊频率范围实现,在光学和近红外频率范围往往失效)而不具备普适性.本文介绍了利用包括非点群对称性在内的晶格对称性来实现Dirac光子晶体的方法,涵盖了二维及三维光子晶体,实现了在高对称点/高对称线上的相对稳定的Dirac点.由于利用晶格对称性的方法并不需要考虑研究对象的粒子属性,可以预见这种方法具有很好的可移植性,包括拓扑声子/弹性波系统在内的经典体系均可以通过这种方式来实现.由此可见,受对称性保护的Dirac点在拓扑系统中的应用仍然值得人们深入研究.

[1]Dirac P A M 1928Proc.R.Soc.London A118 351

[2]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009Rev.Mod.Phys.81 109

[3]Novoselov K S,Jiang Z,Zhang Y,Morozov S V,Stormer H L,Zeitler U,Maan J C,Boebinger G S,Kim P,Geim A K 2007Scinece315 1379

[4]Katsnelson M I,Novoselov K S,Geim A K 2006Nat.Phys.2 620

[5]Shen S Q 2012Topological Insulators:Dirac Equation in Condensed Matters(London,Berlin Heidelberg:Springer-Verlag)

[6]Haldane F D M 1988Phys.Rev.Lett.61 2015

[7]Kane C L,Mele E J 2005Phys.Rev.Lett.95 146802

[8]Kane C L,Mele E J 2005Phys.Rev.Lett.95 226801

[9]Fu L,Kane C L,Mele E J 2007Phys.Rev.Lett.98 106803

[10]Weyl H Z 1929Physik56 330

[11]Haldane F D M,Raghu S 2008Phys.Rev.Lett.100 013904

[12]Wang Z,Chong Y D,Joannopoulos J D,Soljacic M 2008Phys.Rev.Lett.100 013905

[13]Ao X Y,Lin Z F,Chan C T 2009Phys.Rev.B80 033105

[14]Khanikaev A B,Hossein M S,Tse W K,Kargarian M,MacDonald A H,Shvets G 2013Nat.Mater.12 233

[15]Ma T,Khanikaev A B,Hossein M S,Shvets G 2015Phys.Rev.Lett.114 127401

[16]Chen W J,Jiang S J,Chen X D,Zhu B C,Zhou L,Dong J W,Chen C T 2014Nat.Commun.5 5782

[17]He C,Sun X C,Liu X P,Lu M H,Chen Y L,Feng L,ChenY F 2016Proc.Natl.Acad.Sci.USA113 4924

[18]Wu L H,Hu X 2015Phys.Rev.Lett.114 223901

[19]Sabyaschi B,Hirokazu M,Wade D,Edo E,Mohammad H2016New J.Phys.18 113013

[20]Xu L,Wang H X,Xu Y D,Chen H Y,Jiang J H 2016Opt.Express24 18059

[21]Wang H X,Xu L,Chen H Y,Jiang J H 2016Phys.Rev.B93 235155

[22]Wang H X,Chen Y G,Hang Z H,Kee H Y,Jiang J H 2017npj Quantum Materials2 54

[23]Sakoda K 2004 Optical Properties of Photonic Crystals(Berlin:Spring)

[24]Sakoda K 2012Opt.Express20 25181

[25]Mcphedran R C,Nicorovici N A,Mckenzie D R,Botten L C,Parker A R,Rouse G W 2001Aust.J.Chem.54 241

[26]Sanders J V 1964Nature204 1151

[27]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757

[28]Lidorikis E,Sigalas M M,Economou E N,Soukoulis C M 1998Phys.Rev.Lett.81 1405

[29]Yang B J,Nagaosa N 2014Nat.Commun.5 4898

[30]Yang B J,Morimoto T,Furusaki A 2015Phys.Rev.B92 165120

[31]Lu L,Joannopoulos J D,Soljacic M 2013Nat.Photon.7 294

PACS:03.65.Vf,41.20.Jb,42.25.GyDOI:10.7498/aps.66.220302

*Project supported by the National Natural Science Foundation of China(Grant No.11675116)and the Fculty Startup Funding of Soochow University.

†Corresponding author.E-mail:xikeda20072862@163.com

‡Corresponding author.E-mail:joejhjiang@hotmail.com

Dirac photonic crystal∗

Wang Hai-Xiao1)†Xu Lin Jiang Jian-Hua1)2)‡

1)(Department of Physics,Optoelectronics and Energy,Soochow University,Suzhou 215006,China)2)(Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China)

15 August 2017;revised manuscript

31 October 2017)

Dirac Fermion,as one of the basic particles in the particle physics,nowadays have been widely used to describe the electronic states with the behavior of Dirac fermion in the topological electronics.These exotic electronic states are called Dirac point,which exhibited as a linear crossing point in the band structure.Usually Dirac point is the topological phase transition point and thus viewed as the mother state of various topological states.As an analogue of topological electronics,topological photonics,also attracted a great deal of interest due to its potential application.One of the key topic in topological photonics is to realize photonic bands with Dirac point.In this review,we brie fly introduce the progress of Dirac point in the photonic system and focus on the realization method of Dirac point in photonic crystal by take advantage of lattice symmetry.We also discuss Weyl point in the photonic crystal as an extension of the Dirac point.

photonic crystal,Dirac point,topological band,quantum spin Hall e ff ect

10.7498/aps.66.220302

∗国家自然科学基金(批准号:11675116)和苏州大学科研启动基金资助的课题.

†通信作者.E-mail:xikeda20072862@163.com

‡通信作者.E-mail:joejhjiang@hotmail.com