一道高考题的解法与变式
山东 尹承利
一道高考题的解法与变式
山东 尹承利
高考试题大都具有典型性,既对知识与方法进行考查,又对思维缜密性进行考查,在我们教与学的过程中,重视对高考题潜在的知识、方法和应用价值进行挖掘,对于提高分析问题、解决问题的能力是颇为有益的.本文就2017年高考全国数学卷Ⅰ理科第10题(抛物线问题)的解法和变式进行探究,从而达到做一题会一类题、举一反三、触类旁通的效果.
一、试题呈现
例题(2017·全国卷Ⅰ理·10)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,|AB|+|DE|的最小值为
( )
A.16 B.14 C.12 D.10
二、解法分析
分析1.该题考查直线与抛物线(圆锥曲线)的位置关系,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及直线与抛物线(圆锥曲线)的交点问题时,一般都设交点坐标为(x1,y1),(x2,y2),同时把直线方程与抛物线(圆锥曲线)方程联立,消元后,可得x1+x2,x1x2,再把相关弦长用x1,x2表示出来,并代入刚才的x1+x2,x1x2,这种方法即解析几何中的“设而不求”法,可减少计算量,简化解题过程.
解法1.由题意易知直线l1,l2的斜率都存在且不为0.
设直线l1的方程为y=k(x-1)(不妨设kgt;0),

其判别式Δ=[-(2k2+4)]2-4k2·(-k2)=16(1+k2)gt;0.
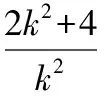
所以由抛物线的定义得
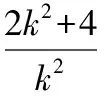


设D(x3,y3),E(x4,y4),则x3+x4=2+4k2,
所以|DE|=x3+x4+p=2+4k2+2=4k2+4.
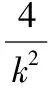
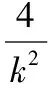
所以|AB|+|DE|取得最小值16.故选A.
点评:本解法取直线的斜率k为参数,设出直线方程并与抛物线方程联立,运用“设而不求”、抛物线定义和均值不等式求解.“设而不求”是数学解题中的一种颇为有用的手段,往往能避免盲目推演而造成的无益的循环运算,从而达到准确、简捷的解题效果.
分析2.由于数学中的定义是建构数学知识的基石,因而抛物线(圆锥曲线)的定义不仅是重要的知识点,也是解答许多数学问题的工具.在解答许多问题时,若能灵活、巧妙地应用抛物线(圆锥曲线)的定义,不仅能深化对抛物线(圆锥曲线)这一数学概念的深刻理解,而且还能提高学生应用定义去分析和解决问题的能力,开拓学生的思维视野.对于过抛物线(圆锥曲线)焦点的直线与抛物线的位置关系(即焦点弦问题)问题常利用抛物线的定义求解,回归定义可使问题的解决变得简单、方便.
解法2.如图,

设AB倾斜角为θ.作AK1垂直准线,AK2垂直x轴.
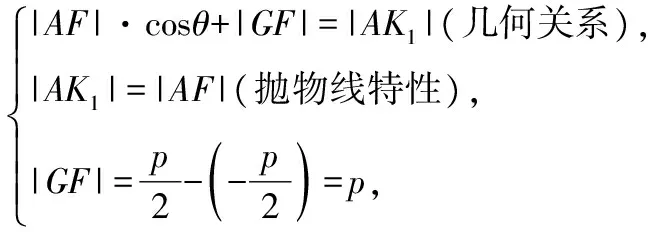
所以|AF|·cosθ+p=|AF|.


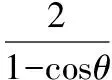

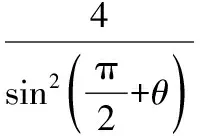
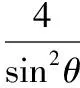
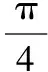
所以|AB|+|DE|的最小值为16.故选A.
点评:本解法取直线的倾斜角θ为参数,运用抛物线的定义、几何关系转化为角θ的正弦函数求解.
上述两种方法是常规方法,需要同学们认真体会和熟练掌握.
通过该题,我们可以得到一般性的结论:已知F为抛物线C:y2=2px(pgt;0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为8p.(证明仿照高考题的两种解法即可)
三、试题变式

( )

分析:由例题的解法2可知
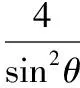



变式2.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,|AB|·|DE|的最小值为
( )
A.64 B.32 C.16 D.10
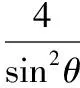
由该变式,我们可以得到一般性的结论:已知F为抛物线C:y2=2px(pgt;0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|·|DE|的最小值为16p2.(证明仿照变式2的解法即可.)
变式3.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,四边形ADBE面积的最小值为
( )
A.64 B.32 C.16 D.10
(1)对移动设备依赖加深。虽然利用碎片时间进行学习,但非教育类的各种类型的微信公众平台也层出不穷,学生在使用本微信公众平台时,有些自制能力差的可能被别的内容吸引,造成时间的浪费。解决这个问题的方法是一方面保证学习资源的质量,另一方面推送些时间管理、自律养成的网文。

由该变式,我们可以得到一般性的结论:已知F为抛物线C:y2=2px(pgt;0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则四边形ADBE面积的最小值为8p2.(证明仿照变式3的解法即可.)
变式4.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,线段AB的中点为M,线段DE的中点为N.
(Ⅰ)求△FMN面积的最小值;
(Ⅱ)求线段MN的中点P的轨迹方程.



(Ⅱ)设线段MN的中点P(x,y),

消去k后得y2=x-3.
故线段MN的中点P的轨迹方程为y2=x-3.
由该变式,我们可以得到一般性的结论:已知F为抛物线C:y2=2px(pgt;0)的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,线段AB的中点为M,线段DE的中点为N,则△FMN面积的最小值为p2.(证明仿照变式4(Ⅰ)的解法即可.)

山东省泰安英雄山中学)

