改进的ANFIS模型在河道堤防物理力学参数反演计算中的应用

齐 奇

改进的ANFIS模型在河道堤防物理力学参数反演计算中的应用

齐 奇

（辽宁省江河流域管理局，辽宁 沈阳 110003）

文章结合自适应函数对传统ANFIS模型进行改进，并将改进的ANFIS模型对辽宁西部某中小河流河道堤防的物理力学参数进行反演计算，并结合正交试验确定模型计算的训练样本，确定改进的ANFIS模型岩石力学参数反演的映射结构，同时结合河道堤防原位监测的位移数据，对改进前后的模型参数反演误差进行了对比分析。结果表明，改进的ANFIS模型可提高河道堤防参数反演精度，相比于传统模型，改进模型的参数反演计算堤顶下降以及周边位移和监测位移之间的误差分别减少14.8%和18.6%。研究成果可在河道堤防参数设计中进行推广和应用。

自适应函数；改进的ANFIS模型；河道堤防物理力学参数反演；反演精度分析

河道堤防稳定性分析和设计需要对堤防物理力学参数进行确定，而对这些力学参数进行准确评估，可提高河道堤防设计的合理性和稳定性，从而确保河道堤防的工程安全。早期，对于河道堤防物理力学参数的确定主要通过原型试验方式进行试验测定［1-3］，但是这种方法需要大量的人力和物力，且由于采样的天然岩石存在较多的裂隙，使得试验测定参数结构和实际结构存在较大的误差。当前，结合试验测定的数据，结合参数反演的计算方法为合理确定河道堤防物理力学参数提供了较为有效的途径［4-6］。这其中传统的ANFIS模型在样本训练计算具有唯一性，且收敛速度较快的特点，近些年来，在许多工程设计中的参数反演得到应用［7-8］，但是传统 ANFIS模型在计算中未能实现参数的优化计算，使得模型计算收敛精度有所欠缺，为此有学者引入自适应函数［9］对传统ANFIS模型进行优化和改进，提高模型收敛精度。为分析改进的ANFIS模型在河道堤防物理力学参数反演中的适用性，本文引入改进的模型，以辽宁西部某中小河流河道堤防物理力学参数进行反演，并结合监测数据，对比改进前后模型的反演计算精度。

1 ANFIS模型河道岩石力学参数反演原理

式中，τ—横向水平状态变量值；α—小波变换函数纵向状态变量值，t—小波神经网络模型计算步长。

在采用小波变换函数进行转换求解后，采用小波分析方法对函数进行分析，分析方程为：

ANFIS模型结合控制方程对模型进行节点计算，各节点控制方程为：

式中，φ（j）—小波神经网络模型隐含层节点控制值；αj—模型计算基础函数；i—小波神经网络模型隐含层节点控制个数；wij—不同状态变量的权重取值；τj—隐含层节点数j时间步长。

在确定模型计算权重后，可以得到小波神经网络模型的目标计算值，计算方程为：

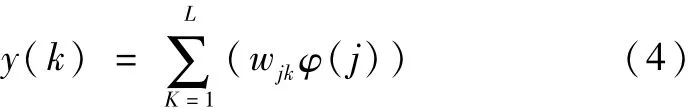
式中，k—计算变量的个数。

在传统模型计算基础上，改进的ANFIS模型采用自适应函数对模型样本数据训练计算进行优化，其中优化的目标函数为：

式中，¯y（k）—训练计算样本数值；y（k）—采用改进的ANFIS模型反演计算值；m—训练样本的个数，结合自适应函数，模型引入效率系数η对传统模型横向和纵向的控制参数进行优化，各参数优化表达式为：

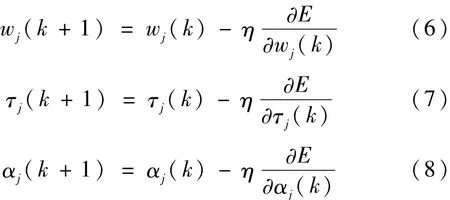
式中，E—自适应函数目标值；其他变量同方程（1）、 （2）、 （3）中所述的变量含义。

2 实例应用

2.1 河道堤防工程概况

本文以辽宁西部某种小河流为实例，该河道堤防长度为4.0km，河堤底部的高程为3.0～5.0m，整个河道堤防的宽度为45m，现状河道堤顶高程为13.5m，河道堤防迎水坡比大部分地段约1∶3，局部较陡处约1∶2.5。河道堤防地层主要为太古界混合岩、古生界大理岩、中生界白垩系安山岩、砾岩及新生界第四系松散堆积层。为分析改进模型在河道堤防岩石力学参数反演计算的适用性，对河道堤防进行了位移和力学参数的观测试验，堤防位移监测点和监测数据见图1和表1。

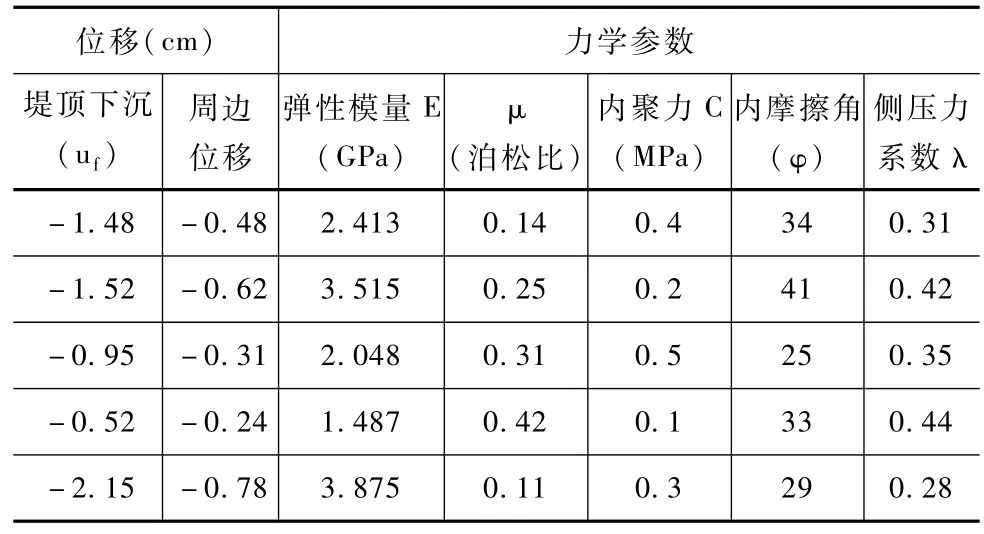
表1 河道堤防原型观测数据

2.2 模型反演参数及取值范围的确定

在模型参数反演计算前，对模型主要的力学参数进行了取值范围的确定，各参数的取值范围间表2。

表2 ANFIS模型参数取值范围

从表中可以看出在取值水平1～6下，河道堤防岩石弹性模量参数的变化范围为1.2～3.7GPa，泊松比的变化范围为0.1～1.1之间，内聚力C的取值范围在0.1～1.2GPa，对于河道堤防稳定较为重要的内摩擦角的取值范围为10～45之间，对于侧向稳定性较为重要的侧压力系数的取值范围为0.20～0.70之间。

2.3 基于ANFIS模型的参数反演计算

2.3.1 河道堤防物理力学反演参数和边坡位移映射关系

图1 河道堤防位移监测示意图

为对模型的收敛度进行分析，采用正交试验的方式确定不同计算方案下的堤顶下沉和周边位移量，分析结果见表3。并结合20组正交试验数据，对改进的ANFIS模型进行了训练，统计不同演算次数下的训练误差分布，结果见图2。

表3 不同计算方案下的参数反演计算结果

图2 各力学参数反演计算误差分布

表3为不同计算方案下的参数反演计算结果，从表中可以看出，当组序从1增加到20后，计算的坝顶沉降值从-1.29cm减少到-0.02cm，其堤防边坡位移从-0.89cm减少到-0.01cm，随着组序的增加，其坝顶沉降和周边位移也逐渐递减。从图2中可以看出，各参数的力学参数反演计算训练误差分布变化规律较为相近，在演算初期，其误差均较大，随着训练次数的增加，由于加入自适应函数对模型训练演算进行优化，使得各个参数的收敛速度均有所加快，各参数反演训练误差的分布曲线均较陡，从图中可以看出，各个参数反演训练次数达到20次时，各参数基本达到最优结果。

2.3.2 基于改进的ANFIS模型的参数反演结果

在模型训练基础上，采用改进的ANFIS模型对河道进行了5组参数反演计算，计算结果见表4。

表4 基于改进的ANFIS模型河道堤防力学参数反演结果

2.3.3 改进前后模型的岩石力学参数反演误差评定结果

为对比分析改进前后的ANFIS模型在河道堤防岩石力学参数反演的精度，结合原型观测试验的数据，对改进前后模型反演计算的位移量进行了误差评定，评定结果见表5和表6。

表5 改进模型误差评定结果

表6 传统模型误差评定结果

从表5中可以看出，在5组监测数据中，改进的ANFIS模型在河道堤防物理力学参数反演计算的堤顶下沉量和监测下沉量之间的误差在-8.8%～-14.0%之间，周边位移之间的误差在9.7%～12.9%之间，各误差均在20%以内。从表6中可以看出，传统ANFIS模型在河道堤防物理力学参数反演计算的堤顶下沉量和监测下沉量之间的误差-23.3%～31.6%之间，周边位移之间的误差在-24.4%～-35.4%之间，各误差均大于20%，相比于传统模型，改进模型的参数反演计算堤顶下降以及周边位移和监测位移之间的误差分别减少14.8%和18.6%。可见，改进的ANFIS模型在河道堤防物理力学参数反演精度好于传统模型，反演精度得到明显改善。

3 结语

本文结合改进的ANFIS模型对河道堤防物理力学参数进行反演计算，并结合辽宁西部某中小河流河道堤防位移和参数测定数据对模型反演精度进行了误差评定，结果表明相比于传统的ANFIS模型，改进模型在物理力学参数反演精度上得到明显改善，为河道堤防工程设计参数确定提供了一种有效的技术手段。

［1］李晓龙.基于支持向量机的岩体力学参数反演及工程应用［D］.郑州大学，2009.

［2］李波，徐宝松，武金坤，等.基于最小二乘支持向量机的大坝力学参数反演［J］.岩土工程学报，2008（11）：1722-1725.

［3］习红凯，马福恒，刘成栋.某碾压混凝土重力坝物理力学参数反演分析［J］.水利规划与设计，2009（02）：45-47.

［4］江小辉，吴文峰.大桥桩基工程对河道堤防边坡变形的影响分析［J］.水利规划与设计，2007（05）：43-45.

［5］王强社，任园园.安康市滨江大道堤防工程工程地质条件及评价［J］.陕西地质，2014（01）：77-81.

［6］向衍，郑东健，何旭升，等.基于MSC.Marc的物理力学参数反演［J］.水电能源科学，2003（04）：7-10.

［7］王永秀，毛德兵，齐庆新.数值模拟中煤岩层物理力学参数确定的研究［J］.煤炭学报，2003（06）：593-597.

［8］张志军，丁德馨，毕忠伟，等.位移反分析的ANN方法与ANFIS方法的比较分析［J］.采矿与安全工程学报，2008（02）：159-163.

［9］马细霞，胡铁成.基于ANFIS的水库年径流预报［J］.水力发电学报，2008（05）：33-36+22.

TP391.41

B

1008-1305（2017）05-0144-04

10.3969/j.issn.1008-1305.2017.05.044

2017-04-06

齐 奇（1988年—），女，工程师。