直坑道内防护门上的爆炸冲击波荷载＊

张亚栋，阿帅磊，邹 宾，于文华

直坑道内防护门上的爆炸冲击波荷载＊

张亚栋1，阿帅磊1，邹 宾1，于文华2

（1.解放军理工大学国防工程学院，江苏 南京210007；2.中国人民解放军66469部队，北京100042）

为可靠开展抗爆结构设计与评估，基于理论计算与数值分析对直坑道内爆炸冲击波荷载的计算问题进行了研究。定量对比分析了现有不同方法计算结果的差异，基于结构响应对不同方法进行了评价，并结合模型实验对近距离爆炸情况下直坑道内防护门上的设计荷载取值问题进行了研究。结果表明，在进行荷载简化时有必要考虑荷载形式与结构响应的耦合，而现有坑道内爆炸冲击波荷载的简化计算方法普遍没有考虑结构动态特性影响，且相互之间存在很大差异，严重影响设计或评估工作的可靠性；近距离爆炸情况下，取门中线上距门边1／4宽度处的压力或门上平均压力作为坑道内防护门上的设计荷载，在比较宽的结构频率范围内是合理的。研究结果可为坑道内结构的防护设计提供参考。

坑道；冲击波荷载；防护门；动态响应

弹药或炸药爆炸在坑道（隧道）内产生的冲击波荷载的计算，是可靠开展工程内部设施设计和评估的基础，对于军事和民用工程都十分重要［1－2］。由于受到坑道壁面约束、反射等影响，炸药在坑道入口附近爆炸时，坑道内流场随着洞口方向、形状以及周围地形的不同，会产生复杂的反射、叠加、扩散等现象，时间历程非常复杂。研究表明，爆炸在坑道内产生的冲击波荷载在距爆心一定距离外会形成稳定的平面波，小于这一距离时坑道断面上各点的压力并不均匀，使得对坑道内的爆炸冲击波荷载的研究要比自由场中困难得多［3］。

坑道内爆炸荷载的实用计算方面已积累了一些方法，具有代表性的有：TM5－855－1方法［4］、WES方法（1984、1997）［5－6］、恩斯特－马赫研究所（EMI）方法［7］、工程兵三所方法［8－9］、工程兵四所方法［3］、后勤工程学院方法［10－11］及我国规范方法等。此外，《终点效应学》［12］等分别基于实验或数值模拟，各自给出过内爆炸情况下坑道（隧道）内冲击波超压计算公式。

对这些方法进行对比发现，不同方法之间差别非常明显：首先不同方法的表达形式差别很大，推荐的适用范围也不相同；有些没有给出明确的使用范围，对于口外、堵口和口内爆炸也未做区分；同时，作为爆炸荷载完整的设计参数，应包含荷载峰值、荷载作用时间、荷载时程曲线等，并非所有方法都能给出全部参数。这表明，目前有关坑道内爆炸荷载的研究还存在许多不确定性，有必要进行更细致的研究。

为掌握炸药爆炸在坑道内产生的冲击波荷载特性以进行可靠的防护设计，本文中对现有的坑道内爆炸冲击波荷载主要研究工作进行对比分析，讨论相互之间的差异，基于结构响应对不同方法进行定量评价，实验与数值计算相结合的方法对坑道内距入口较近距离处防护门上的设计荷载取值问题进行研究，提出相应的设计建议。

1 现有方法的对比分析

1.1 主要参数的对比

坑道内的爆炸冲击波参数主要与炸药量、坑道截面积以及离开爆心的距离有关。为方便比较，将不同方法的计算结果统一整理为比例距离Y＝X／D和比例装药参数z＝D／Q1／3的关系，其中X为防护门距坑道入口的距离，D为坑道断面的等效直径，Q为等效TNT装药量。同时，取不同方法计算结果与我国规范计算结果的比值ak（k＝P、i、τ、y分别代表超压、冲量、正压作用时间及位移）即相对值进行讨论，以直接显示相互之间的差别：

（1）超压峰值

在Y＝1.0～5.0、z＝0.3～2.1m／kg1／3参数范围内对文献中各方法的计算结果进行对比分析，图1（a）、（b）分别为口外与堵口爆炸情况下不同Y值时aP随z的变化情况，图中曲线长短差异显示了各方法不同的适用范围。其中口外爆炸情况下，装药距入口距离为1D。

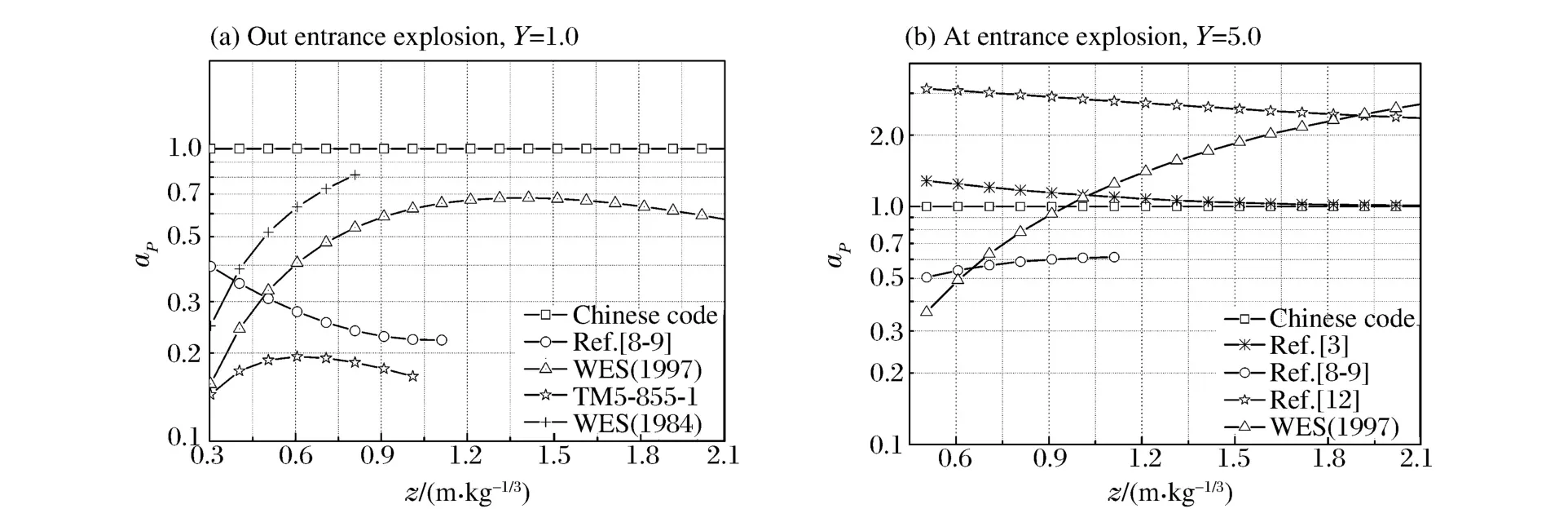
图1 不同方法计算的冲击波超压峰值的比较Fig.1Comparison of peak overpressure from different methods

分析表明，不同方法计算的压力峰值之间的差异是显著且复杂的。口外爆炸情况下各方法计算结果均小于我国规范结果，其中工程兵三所方法计算结果在z值较小处与规范结果的差异小于z值较大处，比规范小60～78%；WES（1997）方法计算结果在z＝0.3m／kg1／3处与我国规范结果相差高达86%，随z的增加差别变小，在z＞0.9m／kg1／3范围内与我国规范差异基本保持36～49%之间；在推荐的使用范围内，TM5－855－1计算结果与我国规范结果相差高达78～81%。堵口爆炸情况下，各方法计算结果与我国规范结果相比有大有小，其中文献［12］方法计算结果较规范结果偏大1.20～2.71倍；工程兵三所方法的计算结果较规范结果整体偏小36～49%，且在Y＝1.0～5.0范围内变化不大；工程兵四所方法的计算结果与规范计算结果相比整体偏大，最大达35%；而WES（1997）方法与规范仍相差显著。

（2）冲量及压力作用时间

如图2所示，Y＝1.0时堵口爆炸情况下各方法计算的冲量与规范结果相比有大有小。其中，工程兵三所方法和后勤工程学院方法计算结果与规范结果的比值均随着z的增大而增大，Y＝1.0时前者从z＝0.3m／kg1／3时的0.76增大到z＝1.1m／kg1／3时的1.68，后者从z＝0.3m／kg1／3时的2.39增大到z＝2.1m／kg1／3时的4.75；工程兵四所方法与规范方法计算结果的比值随Y值和z值的变化较大，在Y＝1.0时，该比值在较小的z值范围内比其他计算方法的比值明显偏高，z＝0.3m／kg1／3处甚至能够达到28.7，但随z 值的增大到1.2m／kg1／3，二者的比值迅速减小并保持在1.0左右。

图2 堵口爆炸情况下的冲量对比Fig.2Comparison of impulse from different methods at entrance explosion

Y＝1.0时口外爆炸情况下各方法计算的等冲量线性衰减压力作用时间与规范结果的比值如图3所示。可以看到，工程兵三所方法预测结果较其他方法都要偏大，且与超压及冲量相反的是该比值随z值的增大而增大，Y＝1.0时比规范结果大39%～175%；而 WES（1984）方法计算结果随z值的变化趋势却是随z增大而减小，图中Y＝1.0时与规范的比值从1.64减小到0.83。

上述结果表明，现有坑道内爆炸冲击波荷载计算方法之间的差异巨大，而且一种方法计算的压力与简化的正压作用时间并非都是比另一种方法计算的结果偏大或偏小。作用时间长短不同的爆炸荷载能够激发结构不同的响应，对于特定结构的设计和抗爆性能评估来说，不同方法造成的结构动态响应的差异就成为需要关注的问题。下面基于单自由度体系，进一步对此进行分析。

图3 口外爆炸情况下的等冲量作用时间对比Fig.3Comparison of equivalent duration of positive phase from different methods in entrance explosion

1.2 对结构响应的影响

参考某实际工程，分别取TNT药量为60.75、117.45kg，坑道横断面积10.5m2，防护门位置距坑道入口5m，换算成 TNT比例装药参数为z＝0.93、0.75m／kg1／3，Y＝0.48。

将前面各方法计算的荷载施加于单自由度系统，计算系统的最大位移响应。考虑结构特性变化，取系统圆频率范围ω＝500～3 000。图4给出了典型的对比情况，其中口外爆炸计算取R＝D。

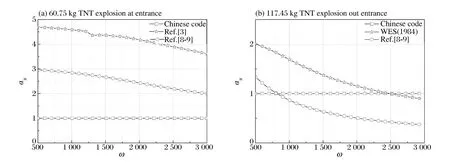
图4 Y＝1.0时不同方法计算的系统最大位移对比Fig.4Comparison of peak displacement from different methods（Y＝1.0）

可以看到，Y＝1.0时堵口爆炸情况下工程兵三所方法计算结果比规范方法计算结果大1.0～2.0倍，工程兵四所方法比规范方法计算结果大3.7～2.6倍，差异均随着结构频率的增大而减小；口外爆炸情况下工程兵三所方法与规范方法计算结果相比在ω＝500时大34%、在ω＝3 000时小63%，而WES（1984）方法与规范方法计算结果相比在ω＝500时大1.0倍、在ω＝3 000时小10%。这表明，在距爆点较近处不同方法计算的结构位移响应存在显著差异，且随结构频率不同而变化。结合前面荷载参数的对比分析说明，以荷载某一参量来评价方法的可靠性是不充分的，需将压力与冲量或压力与正压作用时间共同考虑，并在荷载简化时计入结构动态特性影响，以期在更广泛的工程范围内获得合理的结果，而以往忽略结构直接对荷载进行简化的做法，可能影响结果的可靠性。

2 防护门上的荷载

2.1 数值模型及验证

为分析结构动力特性的影响，参照原型坑道建立流固耦合分析模型进行数值模拟，如图5所示。坑道的横断面尺寸为3.5m×3.5m，防护门安装在坑道内距入口5.0m处，门槛高0.15m，门框宽1.0m，上挡墙高1.35m，钢筋混凝土平板防护门宽b＝1.6m、高h＝2.1m。

为验证数值模拟的有效性，先期建立了坑道结构1∶10的比例模型，如图6所示。完成了29.4、42.0、60.0和142.9g等4种装药量情况下的外爆炸实验，对应的参数范围为Y＝1.21和z＝0.79～1.33m／kg1／3。

图5 某坑道数值分析模型Fig.5Numerical model of a certain tunnel

图6 实验模型Fig.6Tested model

同步采用ANSYS／AUTODYN软件对模型实验进行分析，图7给出了典型的实验与数值模拟得到的模型底端压力波形，表1给出了各炮次下代表测点的特征参数对比情况，其中ΔP、i、t＋及τ0分别为超压峰值、冲量、正压作用时间及等冲量线性衰减压力作用时间。

图7 实验数据与数模模拟结果的对比Fig.7Comparison of numerical results with tested data

表1 数值模拟结果与实验结果的对比Table 1Comparison of numerical results with tested data

通过图7及表1的对比表明，数值模拟的超压峰值与实验结果相比误差在±29%以内，冲量的误差在±36%以内，超压作用时间的误差在±29%以内，等冲量作用时间的误差在±31%以内，均为工程可接受范围，本文数值分析模型是有效的。

2.2 防护门上的压力特征

取防护门上4个压力观测点进行分析，如图8所示，其中点1、2、3分别位于门扇中轴线上距防护门底边h／4、h／2和3h／4处，点4位于门扇水平中线上距门边b／4处。图9给出了不同情况下各点的压力时程曲线。

分析表明，近距离爆炸情况下坑道内防护门上的压力出现了多个峰值，且分布很不均匀：由于装药置于地面，防护门靠近下方的位置首先受到冲击波作用，图9中1点处的冲击波到达时间比点3分别早1.0ms和0.6ms；冲击波超压峰值自下向上逐渐增大，堵口爆炸情况下点3处的超压峰值比1点偏高30%，口外爆炸情况下偏高60%。相比之下，防护门中线上点2和点4的冲击波到达时间及压力峰值均比较接近。

图8 防护门上压力测点Fig.8Position of measuring points

图9 各点的压力曲线Fig.9Overpressure－time histories at different points

2.3 防护门的设计荷载

为进行荷载简化，不同的研究者采用了不同的方法，如文献［3］中取坑道周边壁面压力与断面中心点压力的平均值作为断面上的荷载设计值，文献［8］中测量了距地面1m高处的压力值，文献［11］中则测量了坑道侧壁上的压力；在研究结构内爆炸荷载时，文献［13］中基于结构动力响应等效的原则，提出用墙面短跨三分点处的压力作为设计荷载的简化建议。为了找出能反映防护门动力响应特征的设计均布荷载，分别取如图9所示点1、2、3、4的压力以及门上的平均压力作为荷载代表值，并将其简化为等冲量线性衰减形式，按均布方式施加到门扇上，计算不同荷载代表值作用下防护门的动态位移、支座反力等响应，并与耦合分析模型计算的结果进行对比，按照动力响应相等的原则，取二者吻合最好的荷载代表值作为防护门上的设计荷载。

图10中给出了117.45kg装药口外爆炸时厚度140mm防护门的计算结果，图中y为防护门中点的位移，F为长边方向的支座反力。可以看到，不同荷载代表值作用下的计算结果与数值模拟结果相比，结构动力响应的变化规律能够较好地吻合，但数量有一定差别。在计算最大正向动位移时，点4荷载的计算结果比数值模拟结果偏大25%，而其它荷载的计算结果均比数值模拟结果偏大50%以上；在计算长边的支座动反力时，点4荷载的计算结果比数值模拟结果大4%，而平均荷载的计算结果比数值模拟结果小11%。进一步分析堵口爆炸情况下的结果发现，点4荷载计算的中点位移与数值模型结果最吻合，但平均荷载计算的长边支座反力仅比有限元模拟结果小4.8%，而点4荷载的计算结果比有限元模拟结果小35%。

这表明，为了更准确地计算防护门的动态响应，应选取不同的荷载代表值作为设计荷载：对于位移响应可以取4点荷载作为均布设计荷载，对于支座反力的计算则可以取平均荷载作为均布设计荷载。

图10 口外爆炸情况下防护门动力响应的对比Fig.10Comparison of responses of the blast door in the case of entrance explosion

为检验上述设计荷载取值方法对不同动态特性结构的适用性，通过变化板的厚度，求得具有不同频率特征的防护门的动力响应，与数值模拟结果的对比如图11所示。图中实线为建议的设计荷载的计算结果，虚线为数值模拟结果。由图可见，二者在比较宽的频率范围内都能较好地吻合，总体上数值模拟的位移小于建议设计荷载计算的位移，最大相差15.4%，从设计来说建议荷载对于结构位移计算是偏安全的。

进一步分析表明，建议荷载计算的结构短边支座反力也是稍大于数值模拟结果，但在计算长边支座反力时，数值模拟结果在结构频率较低时大于建议荷载计算的结果，最大偏差达18.7%，在频率较高时偏差减小。从设计角度来说，可以给此时的建议设计荷载乘以1.2的放大系数以保证安全。

图11 不同厚度结构的响应Fig.11Responses of the door with different thicknesses

3 结 论

（1）现有坑道内的爆炸冲击波荷载不同计算方法得到的结果之间存在非常大的差异，必须引起足够的重视。

（2）进行以结构评估或设计为目的的荷载简化时，有必要考虑防护设施的动态特性影响，目前普遍仅就荷载参数进行简化的非耦合作法，可靠性严重不足。

（3）在本文实例的近距离（Y＝0.48、z＝0.75～0.93m／kg1／3）爆炸情况下，坑道内防护门上的设计荷载可取门中线上离门边1／4宽度处的荷载用于位移计算，取门上平均荷载用于支座反力计算并乘以1.2的系数以保证设计安全。与现有计算方法相比，本文中荷载简化方法在比较宽的结构频率范围内具有较高的适用性。

［1］ 徐大力，任新见.爆炸空气冲击波传播规律研究现状与发展趋势浅析［C］∥中国土木工程学会防护工程分会第十三次学术年会论文集.浙江宁波，2012：213－217.

［2］ 于文华.防护门上的爆炸冲击波荷载研究［D］.南京：解放军理工大学，2013.

［3］ 杨科之，杨秀敏.坑道内化爆冲击波的传播规律［J］.爆炸与冲击，2001，21（1）：37－40.Yang Kezhi，Yang Xiumin.Shock waves propagation inside tunnel［J］.Explosion and Shock Waves，2001，21（1）：37－40.

［4］ US Army Engineer Waterways Experiment Station，Department of the Army.Fundamental of protective design for conventional weapon［M］.Vicksburg，1986.

［5］ Britt J R.Attenuation of short duration blast in entranceways and tunnels［C］∥Paul Y T，Ross C A.Proceeding of the 2nd Symposium on the Interaction of Non－nuclear Munitions with Structures.Panama City Beach，Florida，1985：466－471.

［6］ Welch C R.In－tunnel air blast engineering model for internal and external detonations［C］∥Proceeding of the 8th International Symposium on Interaction of the Effects of Munitions with Structures.Mclean，Virginia，1997：195－208.

［7］ Scheklinski G.Blast in tunnels and rooms from cylindrical HE－charges outside the tunnel entrance［C］∥Douglass H M.Proceedings of the 6th Symposium on the International of Non－nuclear Munition with Structures.Panama City Beach，Florida，1993：68－73.

［8］ 何翔，任辉启.305工程内爆炸试验中的冲击波传播规律［J］.防护工程，2002，4（2）：1－8.He Xiang，Ren Huiqi.Shock wave propagation in the 305works inside explosion test［J］.Protective Engineering，2002，4（2）：1－8.

［9］ 庞伟宾，何翔，李茂生，等.空气冲击波在坑道内走时规律的实验研究［J］.爆炸与冲击，2003，23（6）：573－576.Pang Weibin，He Xiang，Li Maosheng，et al.The formula for air blast time of arrival in tunnel［J］.Explosion and Shock Waves，2003，23（6）：573－576.

［10］ 陈海天，李秀地，郑颖人.内爆炸坑道中冲击波冲量试验［J］.后勤工程学院学报，2008，24（2）：6－9.Chen Haitian，Li Xiudi，Zheng Yingren.Scale model tests to determine in－tunnel blast impulse from HE－charges inside the tunnel entrance［J］.Journal of Logistical Engineering University，2008，24（2）：6－9.

［11］ 李秀地，郑颖人.坑道中冲击波冲量传播模型的试验［J］.解放军理工大学学报，2007，8（5）：425－428.Li Xiudi，Zheng Yingren.Scale model tests to determine in－tunnel blast impulse from HE－charges at tunnel entrance［J］.Journal of PLA University of Science and Technology，2007，8（5）：425－428.

［12］ 隋树元，王树山.终点效应学［M］.北京：国防工业出版社，2000：285－289.

［13］ 杨科之，杨秀敏，董军，等.抗内爆炸结构的等效荷载设计法［J］.工程力学，2003（增刊）：599－606.Yang Kezhi，Yang Xiumin，Dong Jun，et al.Equivalent loads method for structures against internal explosion［J］.Engineering Mechanics，2003（suppl）：599－606.

Shock wave loads on the blast door in straight tunnel

Zhang Yadong1，A Shuailei1，Zou Bin1，Yu Wenhua2
（1.College of Defense Engineering，PLA University of Science ＆ Technology，Nanjing210007，Jiangsu，China；2.66469 Troops of PLA，Beijing100042，China）

In order to improve the design and safety assessment of the reliability of blast－resistant structures，we studied the simplified calculation of the shock wave loads caused by HE explosions in straight tunnel based on the theoretical calculation and numerical simulation.Firstly，the differences among existing calculation methods of in－tunnel shock wave loads and their results were evaluated quantitatively in detail and the effects of such differences on structure responses were discussed.Then the design loads on the blast door in a tunnel was studied based on the model test and numerical analysis.The results show that it is important to take into account the coupling effects of the structure response when developing simplified calculation methods for in－tunnel explosion shock wave loads.The existing simplified methods generally disregard such effects and differ from one another significantly，which leads to much more uncertainty in both design and assessment.For close range explosion，the design loads on the door can be taken from pressure at the point on the midline and 1／4door－width away from the door－side，or from the average pressure on the door，which is reasonably acceptable in a wide range of structure frequencies.The present work can provide a reliable method for protection design of in－tunnel structures.

tunnel；shock wave loads；blast door；dynamic response

O383.1 国标学科代码：13035

A

10.11883／1001－1455（2017）06－1057－08

2016－04－12；

2016－06－07

国家自然科学基金创新研究群体科学基金项目（51321064）

张亚栋（1970— ），男，博士，教授，zhydjs＠139.com。

（责任编辑 曾月蓉）