Evasion and pursuit guidance law against defended target

Naiming QI,Qilong SUN,Jun ZHAO

Department of Aerospace Engineering,Harbin Institute of Technology,150001 Harbin,Heilongjiang,China

Evasion and pursuit guidance law against defended target

Naiming QI*,Qilong SUN,Jun ZHAO

Department of Aerospace Engineering,Harbin Institute of Technology,150001 Harbin,Heilongjiang,China

Evasion; Pursuit; Three players; Two parts guidance law; Zero-effort-miss

This paper investigates a new approach for a scenario in which an Attacker attempts to intercept a defended aerial Target.The problem is formulated as a game among three players,an Attacker,a Defender,and a Target,with bounded controls.In the considered pursuit–evasion problem,the Target uses an optimal evasion strategy and the Defender uses an optimal pursuit strategy.The proposed approach focuses on the miss distance as the outcome of the conflict.The infeasible region for the initial Zero-Effort-Miss(ZEM)distance between the Attacker and the Defender,for a scenario in which the Attacker evades the Defender,is analyzed,assuming that the Attacker uses a control effort chosen from the permitted control region.The sufficient conditions are investigated under which,for ideal players,the Attacker can pursue the Target while evading the Defender launched by the Target.The guidance provided on how the Attacker can accomplish the task is divided into two parts.During the final time between the Attacker and the Defender,the Attacker chooses the control effort that guarantees the miss distance,and then uses the optimal pursuit strategy to accomplish the task.The derived guidance law is verified by nonlinear simulation.

1.Introduction

It is difficult for a missile to attack an aircraft that launches a defender because of the rapid development of active defense guidance law.Therefore,feasible guidance law needs to beinvestigated for a missile to attack an aircraft.This problem involves three players,an aircraft(Target),a defending missile(Defender),and an attacking missile(Attacker).

The pursuit–evasion problem is a popular research topic.The interception problem conventionally involves a single missile pursuing a target.Different guidance laws were derived for the two-player scenario.1–3In recent years,various pursuitevasion scenarios involving multiple agents have been developed.A scenario in which two pursuers capture one target was investigated using differential game theory.4–6An approach to address the pursuit–evasion problem with multiple pursuers and one target was presented using cooperative strategy.7,8Boyell9,10derived the kinematic relations for a three-player scenario involving a missile,a moving target,and a counter-weapon under the assumption of constant bearing trajectories.He noted that the moving target determined the optimal course for the counter-weapon.Shinar and Silberman11derived a dynamic game model involving a defender,a missile,and a fixed or slowly moving target.They assumed that the position or the trajectory of the target(if the target moved slowly)was known to both the attacker and the defender,and that the position and the velocity vector of the attacker were provided to the defender.In their model,the attacker had no information about the defender.As a result,to accomplish the task,the attacker had to use a pure random strategy.To accomplish the interception,the defender had to select the starting conditions of the interception randomly to prevent the attacker from avoiding the defender by virtue of the attacker’s greater maneuverability.Rusnak12,13presented a differential game involving three people—a Lady,a Bandit,and a Bodyguard,wherein the Lady sought to maximize her distance from the Bandit in order to evade him.The Bodyguard sought to minimize his distance from the Bandit in order to intercept him.Meanwhile,the Bandit sought to minimize his distance from the Lady by pursuing her.To solve this differential game,an approach based on multiple objective optimization theory was presented,and the required conditions for the solution were discussed.Rusnak14investigated the higherorder players in a problem involving a target,a missile,and a defender.He described a scenario in which the missile sought to minimize the distance to the target,the target sought to maximize the distance from the missile,and the defender tried to intercept the missile prior to its arrival at the target.Ratnoo and Shima,15together with Yamasaki and Balakrishnan16proposed an approach to protect the target,in which a defender used the line-of-sight guidance law to purse the attacker.In this approach,the defender was commanded to be on the line-of-sight between the missile and the target at all times.They demonstrated that this approach yielded better results than the one in which the defender pursued the attacker using a linear guidance law.Refs.17–21presented the cooperative guidance law for the protection of an aircraft.In these papers,the authors derived the cooperative guidance law between the target and the defender against the attacking missile using a linear model.In Refs.22–25,the authors investigated the cooperative guidance law for protecting the target using nonlinear approaches and assumed that the defender could intercept the attacking missile with high heading-angle errors.

Rubinsky and Gutman26,27presented a three-player scenario in which a missile evaded a defender and continued to pursue a target.In this scenario,the target and the defender were independent in the sense that,without helping each other,the target only evaded the missile while the defender only pursued the missile.Later,Shima and Ratnoo28analyzed a threeplayer problem in which an attacker(a missile)and a defender used different guidance laws.They investigated the initial position and launch angles required for the missile to evade the defender.

Most of the abovementioned studies focus on an aircraft’s cooperative protection.The methods within which an attacker can evade the defender and pursue the aircraft were not discussed in detail.A few studies26,27discussed an evasionpursuit guidance law(EPG)in which,when the initial zeroeffort-miss(ZEM)between the attacker and defender and the initial ZEM between the attacker and the target had the same signs,the attacker was designed to evade the defender first.However,in some scenarios,it is not necessary to evade first,and the EPG guidance law is not suitable for the case when the initial ZEM between the attacker and the target is big.In this paper,we derive a new guidance law for the Attacker and analyze the conditions.The presented guidance law can be suitable for the case when the initial ZEM between the Attacker and the Target is big for the suf ficient conditions.The endgame scenario in which an Attacker tries to avoid a Defender launched from a Target and tries to pursue the Target is examined.The Target and the Defender are assumed to use optimal one-to-one evasion and pursuit strategies,respectively.We focus on ZEM to investigate the guidance law and assume that the Attacker uses a control effort chosen from a permitted control region to pursue the Target.The infeasible region of the initial ZEM between the Defender and the Attacker is analyzed.The suf ficient conditions under which the Attacker can pursue the Target while evading a Defender launched by the Target are investigated next.Finally,guidance is provided on the two-part control effort required for the Attacker to accomplish the task.

2.Problem formulation

2.1.Nonlinear kinematics

The endgame scenario considered in this study is illustrated in Fig.1,where in,the problem involves three entities:an Attacker(A),a Target(T),and a Defender(D).It is assumed that the Defender and the Target are independent.The range between the Target and the Attacker and that between the Attacker and the Defender are denoted by RATand RAD,respectively.The velocities of the Attacker,the Target,and the Defender are denoted by VA,VT,and VD,respectively,and their lateral accelerations are denoted by aA,aT,and aD,respectively.The lines of sight between the Target and the Attacker and between the Attacker and the Defender are denoted by LOSATand LOSAD,respectively,and the angles between LOSATand the X axis and between LOSADand the X axis are denoted by λATand λAD,respectively.The flight path angles of the Attacker,the Target,and the Defender are denoted by γA,γT,and γD,respectively.

Neglecting the gravitational force,the geometric relations for the rates of the ranges are given by the following equations:

Fig.1 Engagement geometry.

The LOS rate relations satisfy the following expressions:

The dynamics of each player is considered to be a linear time-invariant system that can be described by the following equations:

Here,xiis the state vector of internal state variables of each agent with dim(xi)=niandrepresents its controller;Ai，bi,Ciand diis the player’s dynamics statespace model matrices.

The path angle relations satisfy

2.2.Linearized kinematics

The problem of against defended target is solved under the assumption that the solution occurs in the endgame phase.This engagement has two collision triangles:that between the Attacker and the Target and that between the Attacker and the Defender.For simplicity,the problem is investigated by assuming that the flight near these collision triangles can be linearized.LOSAT0and LOSAD0are the initial lines of the sight corresponding to LOSATand LOSAD,respectively.The relative displacement between the Attacker and the Target normal to LOSAT0is denoted by yAT.Similarly,the relative displacement between the Attacker and the Defender normal to LOSAD0is denoted by yAD.The accelerations of the Attacker and the Target normal to LOSATare denoted by uALand uTL,respectively.The acceleration of the Defender normal to LOSADis denoted by uDL.The accelerations uAL,uTL,and uDLcan be linearized at the initial lines of sight LOSAT0and LOSAD0by the following expressions:

here,γi0,i= ｛A，T，D｝ represents the initial flight-path angles,λAT0and λAD0denote the initial line-of-sight angles.The controllers of the agents normal to the corresponding LOS are denoted by uA,uTand uDwhich satisfy the following conditions:

It is assumed that the velocity vectors of the three players are not perpendicular to the corresponding LOS throughout the game.The state vector of the linearized engagement is expressed as

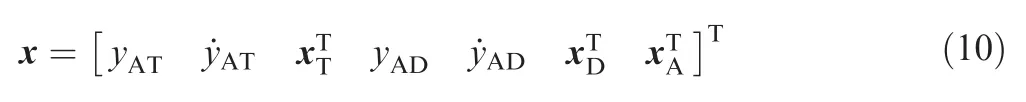
The dimension of x is 4+nA+nT+nD.

The equations of motion corresponding to Eq.(10)are given below:

where

These equations can be expressed in vector form as

By linearizing the kinematics around the collision triangles,the closing speeds between the Attacker(A)and the Target(T)and between A and the Defender(D)can be considered to be constant.These closing speeds are denoted by VATand VADand are expressed as

The intercept times are considered to be fixed and are expressed as

where RAT0and RAD0represent the initial range between A and T,and between A and D,respectively.

For the Defender to intercept the Attacker,the intercept time between the Attacker and the Defender must occur prior to the intercept time between the Attacker and the Target.The Defender is considered to disappear afterA very useful parameteris de fined as

3.Differential game description

3.1.One-to-one optimal guidance law

The order of the problem needs to be reduced so that it can be solved expediently.The well-known ZEM distance transformation can be applied using the following equations:

where ZAD(t)is the ZEM distance between the Attacker and the Defender,and ZAT(t)is the ZEM distance between the Attacker and the Target.andare the transition matrices with respect to Eq.(12),and DADand DATare expressed as follows:

Assuming that A,T,and D obey ideal dynamics,and LOSAT0and LOSAD0are coincidence,Eqs.(16)and(17)can be expressed as

The time derivatives can be expressed as

In this engagement,the final goal of the Attacker is to destroy the Target.While the Attacker pursues the Target,the Defender tries to intercept it.Thus,the Attacker has to guarantee that it can evade the Defender.The cost functions to solve the problem are given by the following expressions:

To simplify the solution,we consider that the Defender and the Target are independent and provide no information to each other.The Hamiltonian function of the problem is expressed as

The adjoint equation and transversality condition are as

and the solutions of Eq.(24)are expressed as

The optimal controllers corresponding to Eq.(21)can be expressed as

The optimal controllers corresponding to Eq.(22)can be expressed as

The closed-form solution corresponding to Eq.(21)can be obtained as follows:

The closed-form solution corresponding to Eq.(22)can be obtained as follows:

3.2.Circumstance of Attacker evading Defender

We now solve the optimal trajectories for A to evade D in order to identify the zone within which A must accomplish the evasion task intuitively.It is assumed thatcan be expressed as follows:

The optimal trajectories for A to evade D are given by the following expression:

Fig.2 Attacker–Defender ZEM optimal trajectories.

It is assumed that the kill radius for D is smaller than R,meaning that ifA can accomplish the evasion task.Wede fineWhen

Thus,we can express the two border trajectories as follows:

The optimal trajectories are shown in Fig.2,and the two border trajectories are highlighted using thicker lines.In the engagement,A and D use optimal strategies to accomplish their respective tasks.If ZADis located within the zone between the two border trajectories,A cannot complete the evasion task,and D wins the differential game.Conversely,if ZADis located outside the zone between the two border trajectories,A wins.Our objective is to make A win the game.Under the optimal strategy,we can obtain the evasion time required for A to win the game.From Eq.(34),we can obtain the following equation:

If the time-to-go for A to evade D is not less than,A is guaranteed to win the game.

3.3.Circumstance for Attacker to pursue Target

We solve the optimal trajectories for A to pursue D to identify the zone within which A can accomplish the pursuit task intuitively.It is assumed thatis expressed as

The optimal trajectories for A to pursue T are expressed as

It is assumed that the kill radius for A is R1,meaning that ifA can accomplish the pursuit task.

Fig.3 Attacker–Target ZEM optimal trajectories.

The optimal trajectories are shown in Fig.3,and the two border trajectories are highlighted using thicker lines.In the engagement,A uses an optimal pursuit strategy,and T uses an optimal evasion strategy.If ZATis located within the zone between the two border trajectories,A can complete the pursuit task.Conversely,if ZATis located outside the zone between the two border trajectories,T wins.The maximum permittedfor A to pursue T is given by the following expression:

4.Different game analysis for Attacker evasion and pursuit

4.1.Area of ZADthat cannot accomplish the task for Attacker when

In order to obtain the sufficient conditions for the Attacker to guarantee the miss distance necessary to avoid the Defender and hit the Target, the special circumstance ofis discussed first.Then,the case whereis analyzed.

Assuming that ZAT(t=0) satis fies 0≤ZAT(t=0)we investigate the conditions required for A to accomplish this task.In this section,only positive values of ZAT(t=0)are discussed.The analysis is the same for negative values.The special scenario whereis discussed first.In this case,A pursues T with maximized accelerationand D and T employ their optimal strategies.For different values ofandwe can determine the required range forZAD(t=0).ZAD(t=0)hastwoboundariesandif ZAD(t=0)is located within the zone between the two boundaries,A cannot accomplish the task.The upper boundary is denoted byandis given by the following expressions:

The lower boundary is represented by,andis given by the following equation:

where t*is the time whenWe know thatThus,

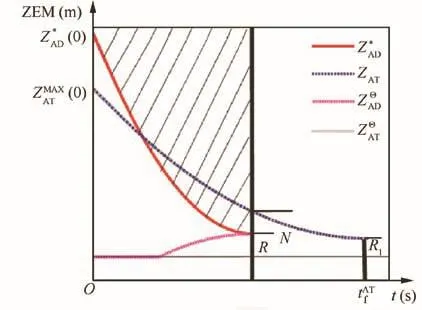
Fig.4 Upper boundary and required area for A to accomplish the task.

Based on Eq.(46),we can obtain the required condition foras follows:

Substituting Eq.(45)into Eq.(47),can be obtained as

Based on Eq.(51),we can then obtain the required condition foras

Fig.5 Lowerboundary forand required area for A to accomplish the task.

Fig.7 shows the shaded area of ZAD(t=0)within which A cannot accomplish the task under the conditionswithand

4.2.Area of ZADthat cannot accomplish the task for Attacker when

We next analyze the condition necessary for A to accomplish the task given thatWe know that if A wants to attack T,the following condition must be satisfied:

Because we have assumed thatZAT(t=0) satisfiesEq.(54)can be written as follows:

here,T*is the time at which ZAT(t=T*)=0.The critical T*is obtained as follows(see the derivation in Appendix A):

The range of uAthat satisfies Eq.(55)can be obtained using the following expression(see the derivation in Appendix A):

where o and κ are given by

Fig.6 Lowe rboundary forand required area for A to accomplish the task.

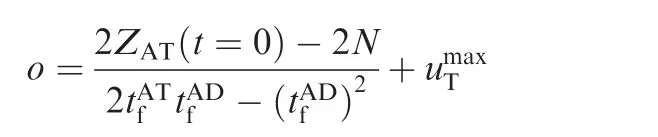
Generally,the following condition always satisfied for T:

This means that within a period of time,if A moves without acceleration,T can evade A and reach a safe area even when ZAT(t=0)=0.From Eq.(57),we obtain the following expression:

Thus,in order to guarantee the miss distance necessary to hit the Target,the control effort must be a positive value when ZAT(t=0)＞0.Eq.(56)can be written as follows:

The range of ZAD(t=0)for which A would be unable to evade D to attack T under the conditions of Eq.(59)is called the infeasible region.It is assumed thatis the upper boundary of this range if uAsatis fies Eq.(59).satis fies the following expression:

Fig.7 Area of ZADthat cannot accomplish the task for A.

The range of uAcan be obtained from Eqs.(62)and(59)as where

Fig.8 Relationship between and uA.

The lower boundary is calculated assuming thatis the lower boundary of the infeasible region for a given uAthat satis fies Eq.(59).is obtained from the expression

Two possible circumstances apply to the initial value of the lower boundary:orThecircumstance is analyzed first,under whichcan be calculated following the steps similar to the one presented in the previous section.Then,the following expression is obtained:

The required condition for uAsatisfying this situation also satis fies the following expression:

Fig.9 Boundaries ofand

Fig.10 Relationship betweenand uA.

The region of uAis given by

The condition required for uAsatisfying this situation also satis fies the following expression:

The region of uAis given by

It should be noted that regardless of whetheris a monotonically increasing function of uA,as shown in Fig.10.Thus,yields the minimal value de fined byifand yields the maximum value de fined byifThe two boundariesandthat encompassandare shown in Fig.11.In the figure,the lines ofandrepresent the time evolutions of the Attacker–Target ZEM corresponding to uA=o andrespectively.When uA=o and uA=min(κ，umaxA),the time evolutions of the Attacker–Defender ZEM correspond to the linesand，respectively.InFig.11,and

The range of uAcan be obtained from Eq.(71)as

where

Fig.11 Boundaries of andfor different circumstances.

The range of uAcan be obtained from Eqs.(59),(67),and(72)as

where

The range of uAcan be obtained from Eq.(74)as

The range of uAcan be obtained from Eqs.(75),(70),and(59)as

where

It can be concluded that under the conditionifuA=o,wecanobtainandThis means that the infeasible region of ZAD(t=0)within which A cannot accomplish its task is the lowest.For different values ofand ZAT(t=0),we can obtain different lowest infeasible regions for ZAD(t=0).Fig.12 shows the lowest infeasible region of ZAD(t=0)within which A cannot accomplish its task for different scenarios.In the figure,

4.3.Guidance law

In the previous section,the highest and lowest infeasible regions for ZAD(t=0)within which A cannot accomplish its task were analyzed,and the required acceleration for A to accomplish the task was investigated.It is known that in the region ofthe infeasible region moves from the lowest infeasible region de fined by O to the highest infeasible region de fined by Ω while uAincreases from o to min(κ).The intersection of O and Ω is de fined by Υ .Thus,if ZAD(t=0)is located in Υ,A cannot accomplish its task using any constant acceleration before time.Conversely,if O and Ω have no intersection,A can always select a reasonably constant acceleration to accomplish its task.O and Ω are given by the following expressions:

Fig.12 Lowest infeasible region of ZAD(t=0)for different circumstances.

Fig.13 Highest infeasible region of ZADfor

Fig.14 Highest infeasible region of

where

where

Υ is then obtained as

The permitted control region for the Attacker to guarantee the miss distance during the final timeis given by the following expressions:

To accomplish the task,the guidance law for the Attacker is divided into two parts.During the final timethe Attacker must choose a control effort in the permitted control region to guarantee the miss-distance necessary to avoid the Defender and hit the Target.Subsequently,the Attacker uses an optimal one-to-one pursuit strategy to hit the Target.

5.Simulations

In this section,the derived guidance law is analyzed by using linear and nonlinear simulations under the given parameters.R and R1are assumed to be 80 m and 3 m.

5.1.Linear simulation

The initial parameters are listed in Table 1.It is assumed that A,T,and D exhibit ideal acceleration dynamics and that the accelerations of T,D,and A are bounded and limited to 50 m/s2,65 m/s2,and 135 m/s2,respectively.

Fig.15 The region of Υ and initial ZAD(t=0)for different initial Attacker’s courses.

Fig.15 shows the region of Υ and the initial ZAD(t=0)for different initial courses of A.If ZAD(t=0)is located in Υ,A cannot accomplish its task using any constant acceleration before the final time.Within the given range of the initial course of A,if the course is located approximately between-1°and 3.29°,the initial ZAD(t=0)is located outside of Υ.This means that an acceleration exists within the permitted control region that guarantees the miss distance necessary to avoid D and hit T.

Fig.16 shows the three control regions corresponding to Eqs.(86)–(88).In the figures,the red lines represent the left parameters and the black lines represent the right parameters corresponding to Eqs.(86)–(88).Thus,in each figure,if the highest red line is located below the lowest black line,the permitted control effort for A to guarantee the miss distance necessary to avoid D and hit T before the final timeexists.If the initial course of A is approximately between-1°and-0.46°,the permitted control region is(o，κ),and if the initial course of A is approximately between-0.46°and 3.29°,the permitted control region is(ξ，κ).Fig.17 shows a linear simulation of the time evolution of the ZEM distance among the three players for different uA,which is within the permitted control effort with different γA0.In Fig.17,the angles and accelerations in the legend present the value of γA0and uA，respectively.It can be seen thatandwhich means A can guarantee the miss distance necessary to avoid D and hit T.

Fig.16 Three control regions for different initial Attacker’s courses.

Fig.17 Linear simulation of time evolution of.ZEM distance.

5.2.Nonlinear simulation

The derived guidance law is veri fied by nonlinear simulation using the parameters shown in Table.1 with γA0=0°.The initial ZAT(t=0)and ZAD(t=0)are 609.707 m and 436.301 m,respectively.We compare the derived guidance law with optimal pursuit guidance law(OPGL).It is assumed that the accelerations of T,D,and A are bounded and limited to 50 m/s2,65 m/s2,and 135 m/s2,respectively.Fig.18 shows the trajectories of the three players using the OPGL.It is noted that the miss distance between A and T,and the miss distance between A and D are 0.112 m and 0.116 m,respectively.Thus,A is intercepted by D.The final time valuesandare 5.9175 s and 3.9415 s,respectively.Fig.19 shows the time evo-lution of the time-to-go from which it can be seen that theis close to linear form,however,exhibits a turning point where ZAThas a very small value close to zero.After the turning point,the accelerations of A and T exhibit the bang-bang phenomenon.

Table 1 Initial parameters.

Fig. 18 Trajectories of three players using OPGL(ZAT(t=0)=609.707 m,ZAD(t=0)=436.301 m).

Fig. 19 Time evolution of time-to-go using OPGL(ZAT(t=0)=609.707 m,ZAD(t=0)=436.301 m).

In order to verify the derived guidance law,we choose the initial acceleration as 85 m/s2(this acceleration is within the permitted control region)for A in the simulation.Figs.20 and 21 show the trajectories of the three players and the time evolution of the time-to-go using the derived guidance law.The miss distances are 98.765 m and 0.383 m;thus,A wins the game.The final time valuesandare 6.2465 s and 3.9515 s.It can be seen that theis close to linear form,however,exhibits a turning point where A changes the guidance law to optimal one-to-one pursuit strategy to hit T.

In order to verify that the derived guidance law can be used universally,we rede fined the initial engagement parameters as shown in Table 2.

Fig.20 Trajectories of three players using the derived guidance law.

Fig.21 Time evolution of time-to-go using the derived guidance law.

Table 2 Initial parameters.

The initial ZAT(t=0)and ZAD(t=0)are 727.195 m and 341.667 m,respectively.It is assumed that the accelerations of T,D,and A are bounded and limited to 50 m/s2,78 m/s2,and 150 m/s2,respectively.As the time evolutions of time-togo are similar to that in the previous section,we only show the trajectories.Fig.22 shows the trajectories of the three players using the OPGL.The miss distances are 0.491 m and 0.103 m as shown in Fig.22 and A is intercepted.The final time valuesandare 6.0281 s and 3.9728 s.We choose the initial acceleration to be 93 m/s2for A to verify the derived guidance law.The trajectories using the derived guidance law are shown in Fig.23.The miss distances are 93.124 m and 0.441 m,and the final time valuesandare 6.2795 s and 4.0105 s,respectively.Thus,A the game.

Fig. 22 Trajectories of three players using OPGL(ZAT(t=0)=727.195 m,ZAD(t=0)=341.667 m).

Fig.23 Trajectories of three players using derived guidance law(ZAT(t=0)=727.195 m,ZAD(t=0)=341.667 m).

6.Conclusions

A new approach for the scenario in which an Attacker intercepts a defended Target was derived by modelling it as a game among three players.Optimal one-to-one evasion and pursuit strategies are assumed to be used by the Target and the Defender,respectively.The approach was verified by nonlinear simulation,and the following conclusions were drawn from the results.

(1)Given the maximized control efforts of the three players,the final timesandthe initial ZEM between the Target and the Attacker,and the initial ZEM between the Attacker and the Defender,the permitted region of control effort for the Attacker to pursue the target successfully can be obtained based on linear dynamics.

(2)Under sufficient situation,before the final timethe Attacker can choose a control effort within the permitted control region to guarantee the miss distance necessary to avoid the Defender and hit the Target.The Attacker then uses an optimal one-to-one pursuit strategy to hit the Target.

(3)The current approach is a two-part guidance law that focuses on the miss distance as the outcome of the conflict.Using the derived guidance law,the Attacker can avoid the Defender and hit the Target.Therefore,this paper can provide designers with a feasible guidance law for a situation where the Attacker evades the Defender and pursues the Target successfully.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(No.11672093)and Shanghai Aerospace Science and Technology Innovation Foundation of China(No.SAST2016039).

Appendix A

To obtain the range of uAthat satis fies Eq.(55),we need to determine the two critical values of uA.One of the critical values of uAsatis fies the following equations:

T*can be obtained by

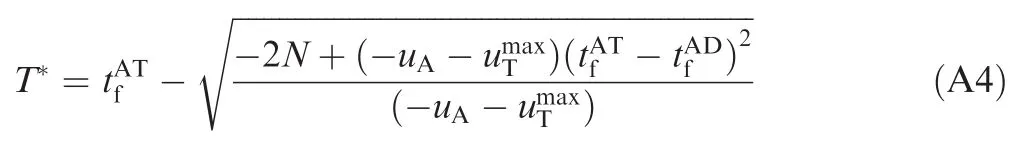
Substituting Eq.(A4)into Eq.(A2),the value of ZAT(t=0)corresponding to Eq.(A1)is obtained from the following equation:

Rewrite Eq.(A5)as

Thus,uAis obtained as follow:

Another critical uAsatis fies the following equation:

Thus,another ZAT(t=0)is obtained as

and uAis obtained as

1.Ho Y,Bryson A,Baron S.Differential games and optimal pursuitevasion strategies.IEEE Trans Autom Control 1965;10(4):385–9.

2.Wang Z,Huang W,Yan Y.Vision-based bio-inspired guidance law for small aerial vehicle.Chin J Aeronaut 2015;423(1):260–7.

3.Song J,Song S.Three-dimensional guidance law based on adaptive integral sliding mode control.Chin J Aeronaut 2016;29(1):202–14.

4.Kumkov SS,Menec SL,Patsko VS.Solvability sets in pursuit problem with two pursuers and one evader.IFAC Proc Vol 2014;47(3):1543–9.

5.Kumkov SS,Menec SL,Patsko VS.Level sets of the value function in differential games with two pursuers and one evader.Interval analysis interpretation.Math Comp Sci 2014;8(8):443–54.

6.Liu Y,Qi N,Tang Z.Linear quadratic differential game strategies with two-pursuit versus single-evader.Chin J Aeronaut 2012;25(6):896–905.

7.Bakolas E,Tsiotras P.Optimal pursuit of moving targets using dynamic voronoi diagrams.In:Proceedings of the 49th IEEE conference on decision and control;2010 December 15–17;Atlanta,Georgia.Piscataway(NJ):IEEE;2010.p.7431–6.

8.Zhao S,Zhou R.Cooperative guidance for multimissile salvo attack.Chin J Aeronaut 2008;21(6):533–9.

9.Boyell RL.Defending a moving target against missile or torpedo attack.IEEE Trans Aerosp Electron Syst 1976;12(4):522–6.

10.Boyell RL.Counter weapon aiming for defense of a moving target.IEEE Trans Aerosp Electron Syst 1980;16(3):402–8.

11.Shinar J,Silberman G.A discrete dynamic game modelling antimissile defense scenarios.Dynam Control 1995;5(1):55–67.

12.Rusnak I.The lady,the bandits and the body-guard game.In:Proceedings of the 44th Israel annual conference on aerospace science;2004 February 25–26.Israel;2004.

13.Rusnak I.The lady,the bandits and the body guards–a two team dynamic game.IFAC Proc Vol 2005;38(1):441–6.

14.Rusnak I.Games based guidance in anti-missile defence for high order participants.In:Proceedings of the 15th IEEE Mediterranean electrotechnical conference;2010 April 25–28.Valletta,Malta.Piscatway(NJ):IEEE;2010.p.812–7.

15.Ratnoo A,Shima T.Line-of-sight interceptor guidance for defending an aircraft.J Guid Control Dyn 2012;34(2):522–32.

16.Yamasaki T,Balakrishnan SN,Takano H.Modi fied command to line-of-sight intercept guidance for aircraft defense.J Guid Control Dyn 2013;36(3):898–902.

17.Perelman A,Shima T,Rusnak I.Cooperative differential games strategies for active aircraft protection from a homing missile.J Guid Control Dyn 2011;34(3):761–73.

18.Shaferman V,Shima T.Cooperative multiple-model adaptive guidance for an aircraft defending missile.J Guid Control Dyn 2010;33(6):1801–13.

19.Shima T.Optimal cooperative pursuit and evasion strategies against a homing missile.J Guid Control Dyn 2011;34(2):414–25.

20.Prokopov O,Shima T.Linear quadratic optimal cooperative strategies for active aircraft protection.J Guid Control Dyn 2013;36(3):753–64.

21.Weiss M,Shima T,Castaneda D,Rusnak I.Minimum effort intercept and evasion guidance algorithms for active aircraft defense.J Guid Control Dyn 2016;39(10):2297–311.

22.Garcia E,Casbeer DW,Pham K,Pachter M.Cooperative aircraft defense from an attacking missile.In:Proceedings of the 53th IEEE conference decision and control;2014 December 15–17.Los Angeles,California.Piscatway(NJ):IEEE;2014.p.2926–31.

23.Garcia E,Casbeer DW,Pachter M.Active target defense differential game with a fast defender.In:Proceedings of American control conference;2015 July 1–3;Chicago,IL.Piscatway(NJ):IEEE;2015.p.3752–7.

24.Garcia E,Casbeer DW,Pachter M.Cooperative strategies for optimal aircraft defense from an attacking missile.J Guid Control Dyn 2015;38(8):1510–20.

25.Kumar SR,Shima T.Cooperative nonlinear guidance strategies for aircraft defense.J Guid Control Dyn 2017;40(1):124–38.

26.Rubinsky S,Gutman S.Three-body guaranteed pursuit and evasion.In:Proceedings of AIAA guidance,navigation,and control conference;2012 Aug 13–16;Minneapolis,Minnesota.Reston(VA):AIAA;2012.

27.Rubinsky S,Gutman S.Three-player pursuit and evasion con flict.J Guid Control Dyn 2014;37(1):98–110.

28.Ratnoo A,Shima T.Guidance strategies against defended aerial targets.J Guid Control Dyn 2012;35(4):1059–68.

30 November 2016;revised 5 January 2017;accepted 3 March 2017

Available online 11 July 2017

Ⓒ2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CCBY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.

E-mail addresses: qinaimingok_hit@163.com (N. QI),sunqilong27@163.com (Q. SUN), zhaojunok_hit@163.com(J.ZHAO).

Peer review under responsibility of Editorial Committee of CJA.