回归系数变点估计的快速非迭代抽样算法

杨丰凯，袁海静

0 引言

变点问题是指在一随机序列中存在某一时刻，使得该时刻两侧的序列服从不同的分布。

从上世纪50年代开始，估计一随机序列中变点的位置成为统计学中的研究热点之一，Chen等[1]详细介绍了各种变点模型及其在遗传学、医药以及金融领域的应用。其中一类问题是研究如何有效地估计线性回归模型中回归系数的变点位置，该类问题可描述为：对于序列yi，i=1，…n， 存在位置 r，p≤r≤n-p，使得：

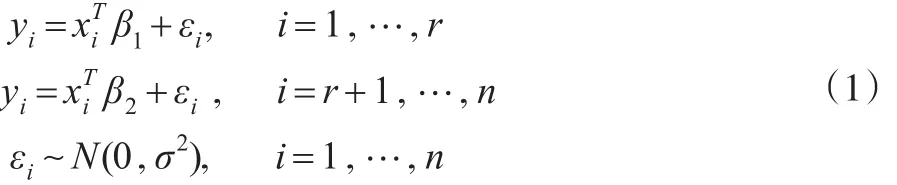
且 εi，i=1，…，n 相 互 独 立 。 其 中 xi=(1，xi1，…xi，p-1)T,β1，β2为不同的 p 维回归系数。本文的目标是估计变点位置r。对于该类问题，文献中的研究方法多是基于似然的方法和贝叶斯方法。其中，Quandt[2,3]发展了基于最大似然估计和似然比检验的回归系数变点检验和估计方法，Kim等[4,5]研究了回归系数变点似然比检验的渐进性质。 Ferreira[6]，Chin Choy 和 Broemeling[7]，Holbert[8]则详细讨论了回归系数变点估计的贝叶斯方法。Chen等[1,9]则从信息论的角度，提出了基于Schwarz信息准则的变点估计方法。基于马氏链蒙特卡洛（MCMC）的Gibbs抽样，由于其灵活性和易实施性，是一种有效的贝叶斯变点估计方法，但Gibbs抽样是一种迭代抽样算法，所抽取的马氏链是否收敛到后验分布很难判断，并且所抽取的样本也很难保证是独立的。Tian等[10]发展了一种基于逆贝叶斯公式的非迭代抽样算法，称为IBF抽样，该算法能够直接从离散的后验分布中抽取独立同分布的样本，然后依据该样本对相关参数做统计推断，从而巧妙地避开了Gibbs抽样的不足之处。Tian等[11]将IBF抽样算法应用到变点问题的研究中，并讨论了泊松变点在医学数据中的应用。Yang等[12]则研究了正态分布均值变点的IBF抽样算法。本文基于Yang等[12]的研究，将IBF算法应用到模型（1）中，讨论估计回归系数变点位置的非迭代抽样算法。分别在弱先验信息和共轭先验信息下给出相应变点位置的精确后验分布，用IBF获得独立同分布的样本，并作相应的统计推断，大量模拟结果显示，该算法能够有效地估计变点位置，并且算法的运行速度比迭代的Gibbs抽样要快很多。

1 无信息先验下正态回归均值变点估计的IBF算法

本文在无信息先验分布下讨论回归系数变点估计的非迭代抽样算法。记 y=(y1，…，yn)T，模型（1）的似然函数为：

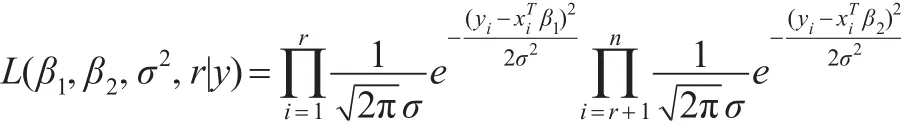
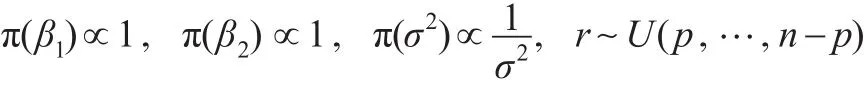
且 β1，β2，σ2，r 相互独立。 其中 U(p，…，n-p)表示 p～(n-p)上的离散均匀分布，“∝”为正比符号。

1.1 无信息先验下的条件分布

参数 (β1，β2，σ2，r)的联合后验分布：

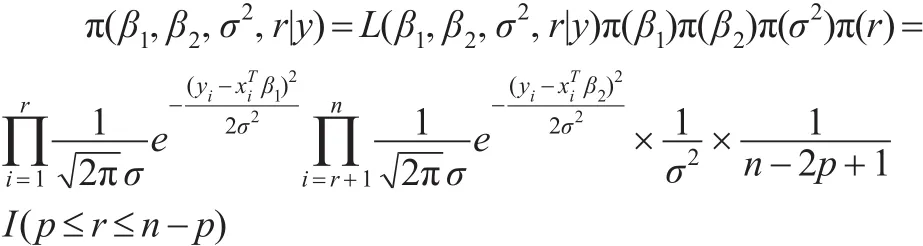
取如下无信息先验分布：

从而变点位置r的条件后验分布为：

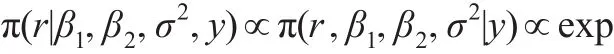
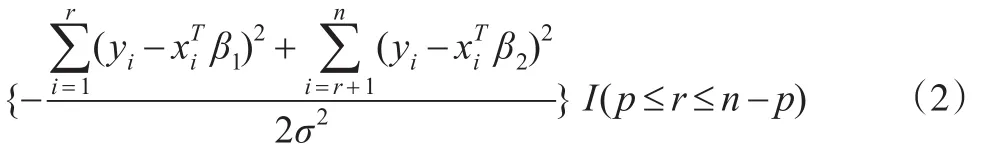
而：

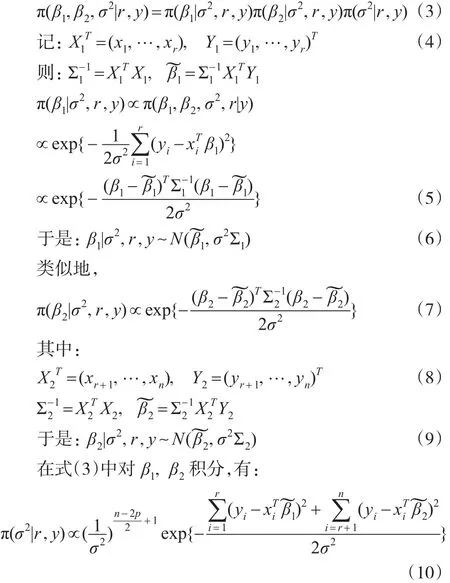
上式右端为逆伽马分布的密度的核，故有：

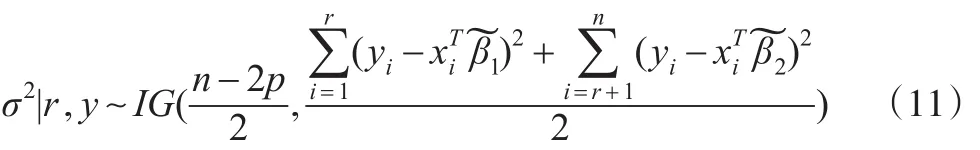
其中 IG(a，b)表示参数为a，b的逆伽马分布。

1.2 IBF算法

根据Tian等[10,11]所提出的离散缺失数据分析的IBF算法的思想，有：

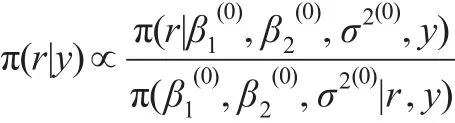
IBF抽样算法分以下几步：

第一步：计算

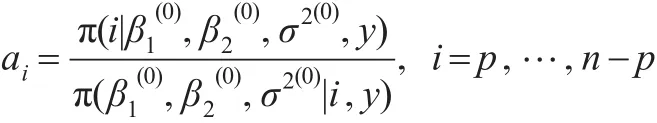
则变点位置r的精确后验分布为：

P(r=i|y)=λi，i=p，…，n-p

第二步：以概率 λ=(λp，…，λn-p)从集合 S={p，…，布π(r|y)的独立同分布的样本，可以根据该样本对r作统计推断。

第三步：对 l=1，…，L,根据式（11）、式（6）和式（9），分别产生：

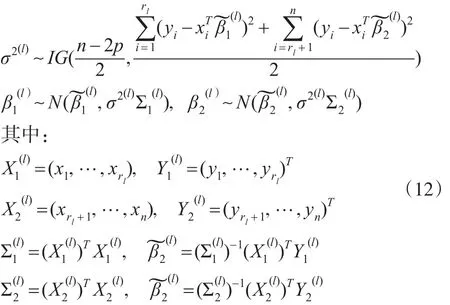
2 共轭先验下正态回归均值变点估计的IBF算法

在共轭先验下研究正态回归均值变点估计的IBF算法，取如下先验分布：

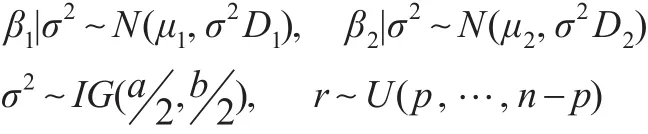
其中μ1、μ2均为 p维常向量，D1、D2均为 p阶正定阵，IG(a2，b2)表示参数为a2和b2的逆伽玛分布。在此假设 β1，β2关于 σ2条件独立,且 (β1，β2，σ2)与 r 相互独立。

2.1 共轭先验下的条件分布

参数 (β1，β2，σ2，r)的联合后验分布：

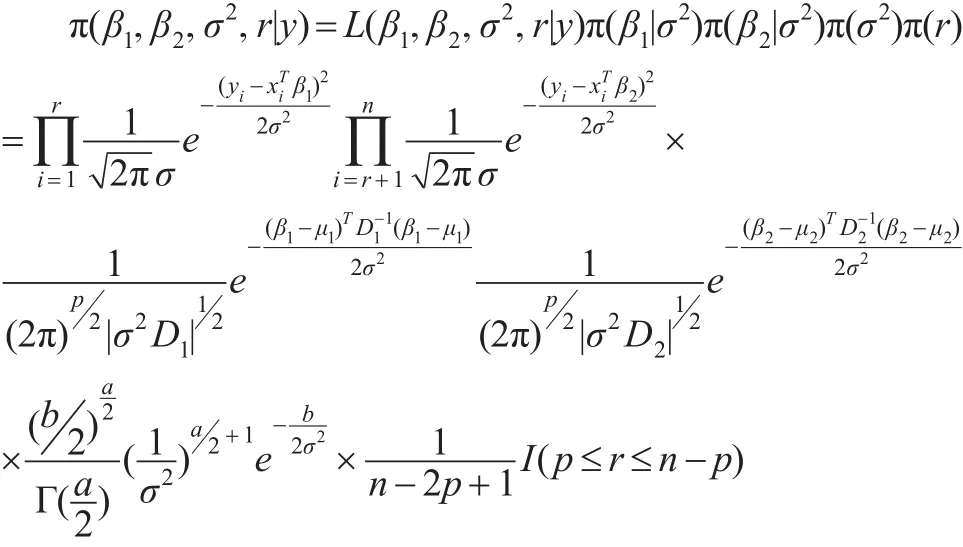
从而变点位置r的条件后验分布为：

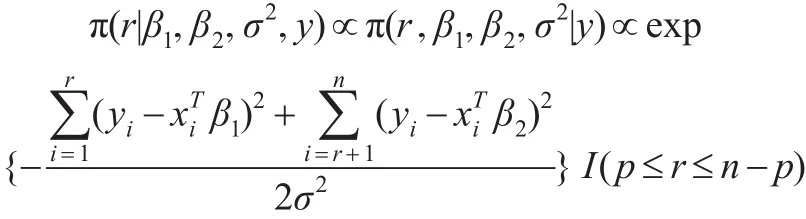
该分布与式（2）相同，与先验分布的选取无关。而：

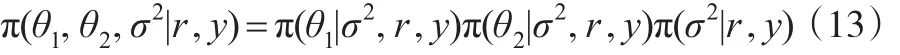
分别计算上式等号右端的三个条件分布。易见：

2.2 IBF算法

类似无信息先验下的IBF算法，有：

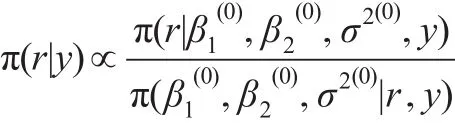
步骤3：对l=1，…，L,根据式（19）、式（15）和式（17），分别产生：

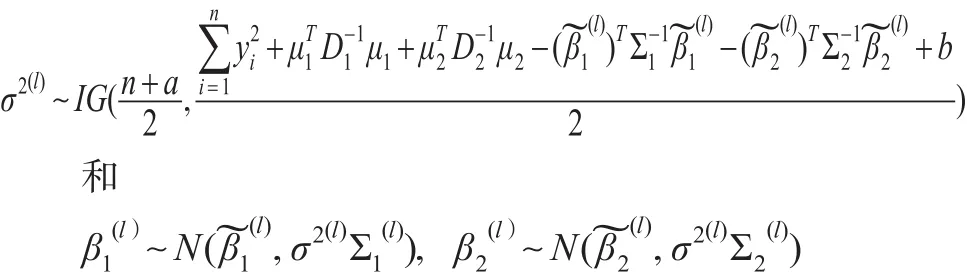
其中：

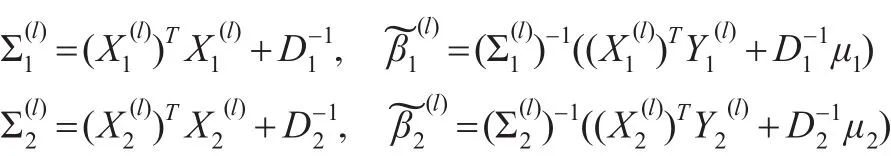
3 模拟

通过模拟，研究用IBF算法估计回归系数变点位置的效果，并与迭代的Gibbs抽样算法作比较。考虑如下单变点一元线性回归模型：

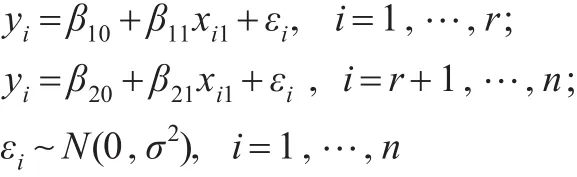
假设εi，i=1，…，n相互独立。在此取n=200，β10=选取变点位置r=40，60，80，100，120 ， 140，160。重复试验200次，在每次实验中分别实施IBF算法和Gibbs抽样算法对变点位置进行估计。在第i次试验中，记：

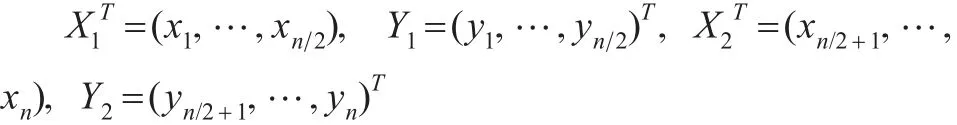
分别取前一半数据和后一半数据所得最小二乘估计作为初值，即有：

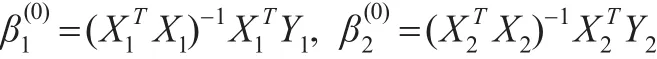
取σ2(0)=1。在Gibbs抽样中，取r(0)=100。采取基于样本的共轭先验分布，其中：

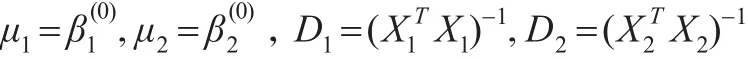
分别模拟产生变点位置r的L=6000个IBF样本和L=6000个Gibbs样本，并舍去前3000个作为burn-in样本，方误差的平方根（RMS）来衡量估计的精度，即有：

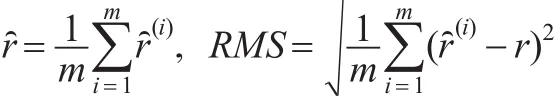
模拟结果如表1所示。

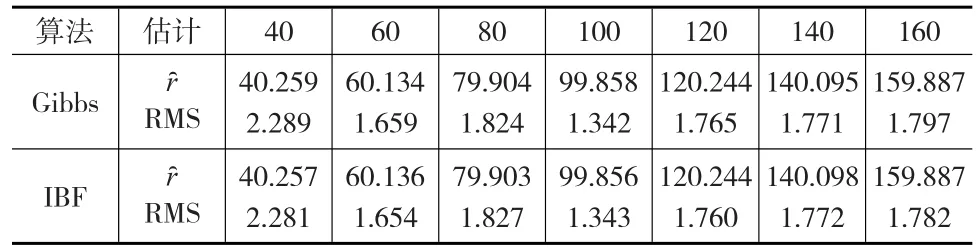
表1 对不同的变点位置，两种算法的结果比较

表1显示不论真实变点在何位置，两种算法所得估计ȓ都很接近真实变点位置，并且估计的精度RMS都很小，说明两种算法对真实的变点位置不敏感，都能够有效地估计变点位置，并且两种算法所得估计ȓ以及估计的精度RMS相差微乎其微。

比较对于产生相同的样本量的两种算法的计算时间。以r=80为例，本文取J分别为200,400,800,1000,3000,6000,10000,20000。共做200次重复试验，这200次试验的平均运行时间time(s)及r的估计ȓ和均方误差的平方根（RMS）见表2。

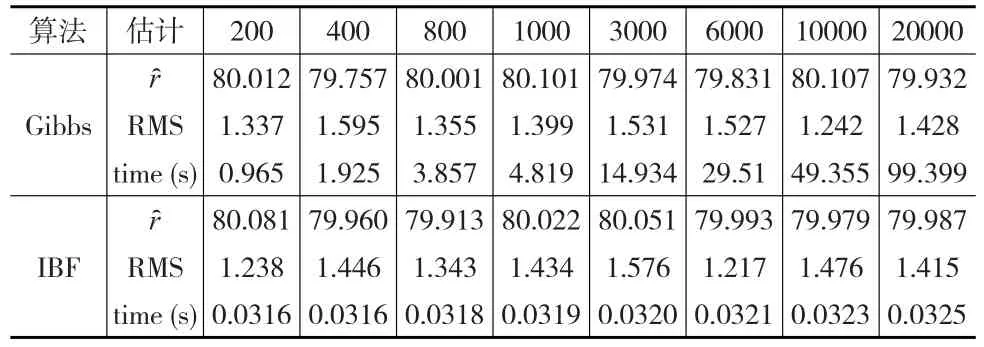
表2 对不同的样本量两种算法的结果比较

从表2可以看出，对不同的样本量，两种算法所得变点位置的估计值都很接近真值，所得估计的RMS都很小，说明这两种算法都很有效。但两种算法所产生相同样本量的运行时间却相差很大。当J从200增加到20000时，200次试验中IBF算法的平均运行时间在0.0316秒到0.0325秒之间，相差只有0.0009秒，变化微乎其微；与之对比，Gibbs抽样的平均运行时间从0.965秒增大到99.399秒，后者是前者的大约100倍。纵向来比，产生J个样本的时间比Gibbs/IBF，当J=200时，该比值为30.54；当J=20000时，该比值增大到3058.43。说明要产生相同的样本量J=20000，Gibbs抽样的运行时间是IBF算法的运行时间的3058.43倍。可见IBF抽样比Gibbs抽样快很多，特别是产生大样本时。

4 结论

本文提出了估计线性回归模型中回归系数变点位置的非迭代抽样算法（IBF），该算法能够获得变点位置的精确后验分布，进而得到该后验分布的的独立同分布的样本,然后依据该样本对变点位置做统计推断。该算法巧妙地避开了Gibbs抽样等MCMC方法的收敛性诊断问题，所获样本为简单随机样本，可直接用来进行统计推断。模拟显示该算法能够有效地估计未知变点位置，并且与迭代的Gibbs抽样相比，该非迭代抽样算法的运行时间大大缩短。

[1]Chen J,Gupta A K.Parametric Statistical Change Point Analysis:With Applications to Genetics,Medicine,and Finance(2nd edition)[M].Boston:Birkhauser,2012.

[2]Quandt R E.The Estimation of The Parameters of a Linear Regression System Obeys Two Separate Regimes[J].Journal of the American Statistical Association,1958,(53).

[3]Quandt R E.Tests of the Hypothesis That a Linear Regression System Obeys Two Separate Regimes[J].Journal of the American Statistical Association,1960,(55).

[4]Kim H J,Siegmund D.The Likelihood Ratio Test for a Change-Point in Simple Linear Regression[J].Biometrika,1989,76(3).

[5]Kim H J.Tests for a Change-point in Linear Regression[J].IMS Lecture Notes-Monograph Series,1994,(23).

[6]Ferreira P E.A Bayesian Analysis of a Switching Regression Model:Known Number of Regimes[J].Journal of the American Statistical Association,1975,(70).

[7]Chin Choy J H,Broemeling L D.Some Bayesian Inferences for a Changing Linear Model[J].Technometrics,1980,(22).

[8]Holbert D.A Bayesian Analysis of a Switching Linear Model[J].Journal of Econometrics,1982,(19).

[9]Chen J.Testing for a Change Point in Linear Regression Models[J].Communications in Statistics-Theory and Methods,1998,(27).

[10]Tian G L,Tan M,Ng K W.An Exact Non-iterative Sampling Procedure for Discrete Missing Data Problems[J].Statistica Neerlandica,2007,61(2).

[11]Tian G L,Ng K W,Li K C et al.Non-iterative Sampling-based Bayesian Methods for Identifying Change Points in the Sequence of Cases of Hemolytic Uremic Syndrome[J].Computational Statistics and Data Analysis,2009,53(9).

[12]杨丰凯，袁海静.正态均值变点识别的非迭代抽样算法[J].统计与决策,2016，（8）.