基于改进粒子群算法的微电网能量管理系统的优化
郑梦秋,薛阳,王琳
(上海电力学院自动化工程学院,上海 200090)
0 引言
在微电网运行中,由于风力、光照具有不稳定性和不可控性,而分布式电源运行受天气影响因素较大,且家庭中的日常负荷在运行中也有一定的波动性,因此一般孤岛下的微网系统很难能够满足自给自足,非常不稳定。但是通过配置适量容量大小的储能单元,可以与微网系统协同合作,有效提高微网的安全性,可靠性以及经济性。当风光等分布式能源不足以提供负荷所需功率时,由储能系统提供额外所需功率,反之则由储能单元储存剩余的功率。
本文在综合考虑了风光发电单元、负荷特性,功率约束等问题后,构造出以蓄电池加超级电容器的储能系统,并用递减权重法改进粒子群算法来对算例进行求解,并证明了这种基于粒子群优化算法的容量配置的正确性。
1 微电网能量优化调度的建模
微电网的稳定、安全运行的关键在于其储能管理系统的运作。而储能系统的优化能够使微网系统更加安全地运行。在微网系统中的各分布式电源、冷热电负荷、蓄电池等不同特性,优化微网中各发电单元的出力与储能系统充放电管理的平衡需求以及负荷波动等要求下,来完成微网系统的发电成本,以及污染物排放的最小化,满足总效益的最佳原则。
微网系统运行中的各约束条件如下:
孤岛下的微电网,其储能系统的优化是使其经济性达到最优,其次在达到经济投资的最低标准下,系统的整个污染物排放量最低。其目标函数可以用下式表示:minZcost=λ1Cg+λ2Ce
式中:
Zcost——微网系统所需资金的目标函数;
Cg——系统发电成本;
Ce——污染物排放成本;
λ1,λ2——Cg与Ce的权重比。
根据孤岛下微电网系统运作的状况可以了解,约束条件主要包括发电盈余、发电不足、功率平衡以及分布式单元出力约束等。
发电盈余约束:
在微网运行中,令i(1≤i≤12)月系统发电量盈余最多,总发电量用 E(i)表示。设 n 为当月天数,则 E(i)/n为每天微网系统发电的盈余量。为当微网系统发电总量比日常负荷需求还要多时,应让储能单元将盈余的能量储存起来。为了避免过多的储能单元处于空闲状态,一般储能系统的容量配置要小于日均多余的电量,也就是配置的储能总量应当小于n1E(i)/n,其中n1为储能系统恢复时间。表达式如(1):

发电不足约束:
当微网系统发电总量小于负荷所需的情况下,则应由储能系统供给负荷所需额外电量。令第j月负荷所需电量最大,月电量缺损用Ej表示,平均每天的电量缺损为E(j)/n。为了保证微电网系统在恶劣环境下也能为负荷供给足够电量,配置的储能总量应大于n2E(i)/n,其中n2为给定的时间。表达式如(2):

功率平衡约束:
在大容量混合储能系统中,蓄电池作为储能装置一般负责绝大部分的能量存储的任务,但是在面对负荷系统出现波动时,蓄电池效果并不理想,而如果将超级电容用作储能的辅助装置,通过超级电容器能够快速充放电的特性,发挥其大功率吞吐能力的优势,能够较好地解决负荷系统功率波动的问题。考虑极限情况下,在没有分布式单元发电情况下,储能系统的功率输出能力应大于峰值负荷,具体表达式如(3):

式中:
t——Gi冲击负荷持续时间;
PLmax——冲击负荷功率。
分布式单元出力约束:
微网中各分布式单元必须按要求,满足各单元发电出力约束,这样才能使整个微网系统安全稳定运行。分布式单元发电出力约束如(4):

2 改进粒子群算法
粒子群算法是通过观察鸟群在一定空间内随机搜索食物的群体行为而得到的一种算法,一般用来解决最优化问题。在粒子群算法中,每一个个体都看作是正在寻找食物的一只鸟,即代表需求解问题中的潜在答案,每一个粒子在寻找最优解时,都会赋给它们一个决定寻找的方向和距离,然后每一个粒子都会跟随当前区域内的最优粒子继续寻找。本文采用惯性权重法来计算粒子的速度,如式(5)所示。
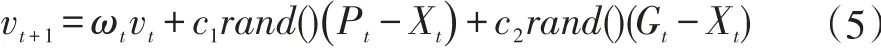
粒子群算法在实际应用当中,惯性权重ωt是计算机仿真过程中,比较影响系统的优化结果因素之一。它是体现当前粒子继承上一粒子速度大小的比重。为了使该算法具有较理想的结果,本文采用递减权重法,如式(6)。
随着粒子迭代更新的进行,式(5)中的ω大小由ωmax递减至ωmin,通过反复实验,其中参数ωmax取值为9.0,ωmin取值为4.0的情况下,既可以保持算法前期在全局下的收敛能力,又可以再算法后期使粒子保持更精确的局部探索。式(6)中,t:当下迭代次数;T:最大迭代次数。

改进粒子群算法优化微网储能配置容量流程图:

图1 流程图
3 算例分析
本文以孤岛运行下的微电网为仿真对象,由MAT⁃LAB软件进行仿真验证。
仿真实例中参数如下:
分布式发电装置中,风机额定功率为70kW,光伏额定功率为20kW。通过查找浙江某小岛资料得到,岛上每月分布式电源发电量如图2、图3所示。风速参照中国气象数据网,通过风机扇叶的切入、切除风速,进而得到风力发电单元月发电总量。光伏发电单元的发电效率主要受光照辐射强度影响较大,温度因素可忽略不计。

图2

图3
单体蓄电池和超级电容器的基本参数如表1。
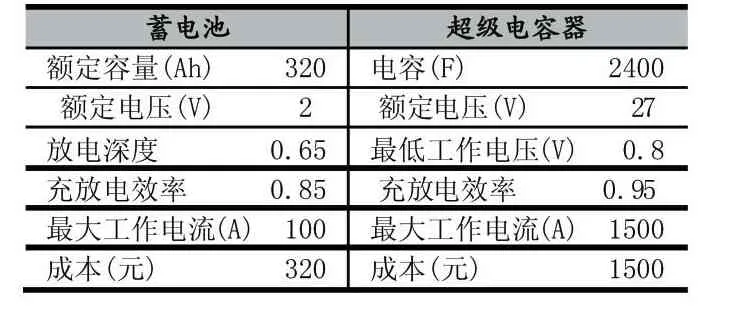
表1
仿真过程中,设置粒子群种群规模size=150,加速因子a1=a2=1.4950,ω随式(6)递减。经过300次算法迭代,得到目标函数的最小值,仿真过程的迭代如下图4所示。通过对比可以观察到,改进后的算法结果避免了粒子较早收敛,提高了搜索精度。容量优化的最终配置如表2所示。

表2
由表2可得如果单单用蓄电池作为储能系统的配置,则为了解决冲击负荷的高要求,需要安装较多的蓄电池单元,经济上非常不划算,而将蓄电池与超级电容器按一定比例混合搭配,既能够保证有足够能量储存,又能够发挥超级电容大功率吞吐的特性,使得整个储能系统达到经济最优的目的。
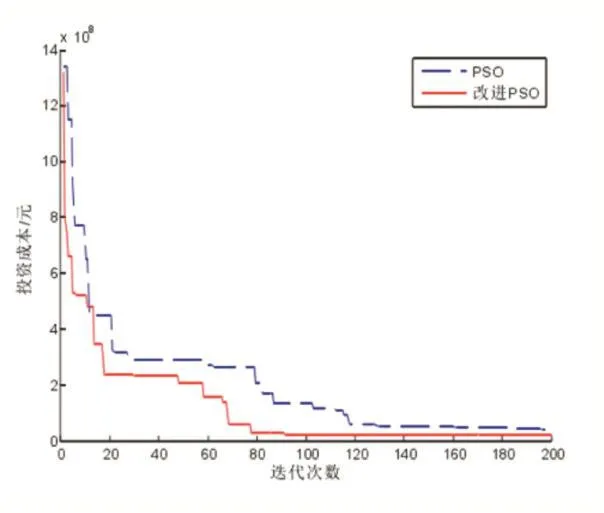
图4
通过表2的结果可以看到,采购435个蓄电池和38个超级电容,将蓄电池用5×87的结构串并联为一组,每组的额定电压为220V,额定电流100A。再将38个超级电容器全部串联成一组,组合后超级电容器组的额定电压为100V、容量是65F。
4 结语
本文将改进后的粒子群算法应用于微电网中储能系统的配置优化,利用改变惯性权重,调整惯性因子的方法,提高了算法搜索能力,减小搜索空间,基于月平均电量提了储能配置优化的约束方程,将改进后的粒子群算法对文中实例进行求解优化。计算结果证明了基于改进粒子群算法的储能配置容量上经济的优越性,并使得整个微网系统运行更加安全、可靠、稳定。
[1]张建华,苏玲,陈勇等.微网的能量管理及其控制策略[J].电网技术,2011,35(7):24-28.
[2]马溪原,吴耀文,方华亮等.基于可靠性评估的微电网配置方法[J].电力系统自动化,2014,35(9):73-77,99.
[3]汪海瑛,白晓民,许婧.考虑风光储协调运行的可靠性评估[J].中国电机工程学报,2012,32(13):13-20.
[4]任磊,谢开贵,胡博等.计及运行策略的微电网可靠性评估[J].电力系统保护与控制,2013,41(15):21-29.
[5]丁明,王波,赵波等.独立风光柴储微网系统容量优化配置[J].电网技术,2013,37(3):576-581.
[6]Wang S,Li Z,Wu L,et al.New Metrics for Assessing the Reliability and Economics of Microgrids in Distribution System[J].IEEE Transactions on Power System,2013,28(3):2852-2861.
[7]Niemoeller B.A.,Krein P.T.Battery-Ultracapacitor Active Parallel Interface with Indirect Control of Battery Current[C].Power and Energy Conference at Illinois(PECI),2010:12-15.
[8]刘建涛,张建成,王珂等.独立光伏发电混合储能系统容量优化研究[J].电网与清洁能源,2012,28(3):85-90.
[9]杨珺,张建成,黄磊磊.基于改进粒子群算法的独立光伏发电系统储能容量优化配置研究[J].华东电力,2012,40(8):1370-1374.
[10]周志敏,纪爱华.离网风光互补发电技术及工程应用[M].北京:人民邮电出版社,2011.81-85.

