LGM模型中缺失数据处理方法的比较：ML方法与Diggle-Kenward选择模型*

张杉杉 陈 楠 刘红云

(1首都经济贸易大学劳动经济学院,北京 100070)(2北京师范大学心理学院应用实验心理北京市重点实验室,北京 100875)(3艾美仕市场调研咨询(上海)有限公司,北京 100005)

1 引言

追踪研究(Longitudinal Study)通过在一段时间内,对个体的某种或某些特征进行有系统的、定期的观测,来探讨特质发生、发展以及变化的特点。在追踪研究中,研究者虽尽量使得前后观测样本相同,但是由于追踪研究耗时较长,被试常常会因为个体特质或者其他外部影响因素而退出实验,造成大量的缺失情况。追踪研究中数据的缺失是研究者普遍会面临的问题,但是如何选取合适的处理方法并不容易。

缺失数据处理方法的选择依赖于缺失数据产生的机制以及缺失模式。缺失数据机制描述了缺失数据与该数据集中变量的真实值之间,以及与协变量之间的关系,主要有完全随机缺失(Missing Completely at Random,MCAR)、随机缺失(Missing at Random,MAR)和非随机缺失(Missing Not at Random,MNAR)三种。前两种情况下缺失值被视为可忽略的(Little &Rubin,2002),而非随机缺失机制常被视为是不可忽略的(Power et al.,2012),所谓“不可忽略”,指的是非随机缺失的数据不能够作为其来源完整数据的有效代表,因此如果仅用非随机缺失后的完整数据进行统计分析,将得到有偏的参数估计结果,甚至可能得到无效的结论 (Schafer &Graham,2002;Little &Rubin,2002)。

关于缺失数据处理方法的研究颇受重视,大量的研究表明,研究者常用的一些简单的缺失数据处理方法,如列删除(Listwise Deletion)和对删除(Pairwise Deletion),单一插补的方法,由于其得到的参数估计结果有偏,检验力下降等种种局限性,并不推荐使用(Enders,2010)。近年来,关于缺失数据处理方法的研究主要集中在MAR缺失机制下的探讨,其中多重插补法和极大似然估计法是应用最广泛的两种方法(Rotnitzky,2009)。对于MNAR缺失机制的数据,研究者也提出了一系列的处理方法(Albert &Follmann,2009;Enders,2011a,2011b )。

对于非随机缺失数据的处理,由于需要描述缺失机制与目标变量的关系,其处理方法大多是采用基于模型的方法 (Little &Rubin,2002)。对于有非随机缺失的追踪数据的分析过程,则是在增长模型的基础上加入一个描述缺失特征的模型来矫正偏差(叶素静,唐文清,张敏强,曹魏聪,2014)。Heckman (1976)首先将选择模型作为处理追踪数据中MNAR缺失的方法,此后引起研究者广泛关注。Little 和 Rubin (2002)、Schafer和 Graham (2002)推荐使用选择模型(Selection Modeling)和模式混合模型(Pattern-Mixture Modeling)来处理MNAR缺失数据。基于潜变量增长模型衍生出不同的处理非随机缺失数据的模型,如Wu和Carroll (1988)模型、Diggle和Kenward (1994)选择模型(以下简称D-K选择模型)等,进一步在这些模型的基础上添加潜类别变量,可以更加完善地处理带有 MNAR缺失数据的增长模型,如Beunckens,Molenberghs,Verbeke和Mallinckrodt (2008)潜类别选择模型、D-K潜类别选择模型(Muthén,Asparouhov,Hunter,&Leuchter,2011)、Roy(2003)潜类别模式混合模型和 Muthén-Roy潜类别模式混合模型模型(Muthén et al.,2011)等。这些基于模型的 NMAR处理方法也逐渐用于应用研究中。但在实际应用中,由于选择模型和模式混合模型基于不同的缺失机制的假设,且这些假设本身无法检验,因此很难对两类方法进行比较。本研究主要考虑选择模型非随机缺失机制的假设条件下,探讨D-K模型在处理缺失数据时的表现。

2 问题提出

虽然目前已有许多 MNAR数据的处理方法,在实际研究中也得以应用,但 MNAR数据处理方法的选择对研究者来说仍存在困难。首先,在MNAR机制下各类处理方法都需要满足一定的前提假设,有研究者指出基于 MNAR机制下的处理方法可能会对缺失机制和正态分布的假设比较敏感(Enders,2011a,2011b)。但这一结论尚缺乏实证研究的证据。另外,对于MNAR缺失数据,如果正态性假设不满足,这些基于模型的处理方法是否具有稳健性仍需要进一步研究。同时,实际中MNAR缺失下方法选择的问题,仍存在争论。有研究者指出,如果忽略MNAR缺失机制而使用MAR假设下的模型会带来估计上的偏差;但也有观点认为,即使在违背假设的情况下,一个好的 MAR模型仍然要优于差的MNAR模型(Schafer,2003)。因此,在MNAR机制下,如果采用了基于MAR的稳健极大似然估计,其结果与基于 MNAR的模型分析方法相比,其表现是否也不逊色？另一方面,在 MAR机制下,如果采用基于MNAR的模型处理方法,其结果与 MAR下的稳健极大似然估计是否存在差异。在目前尚无明确的检验数据MAR和MNAR缺失机制的方法下,对这些问题的探讨,无疑对实际追踪研究中,缺失数据处理方法的选择很有价值。

基于上述问题,本文主要通过模拟研究的方法探讨以下几个问题：(1)在 MNAR缺失数据下,当目标变量不服从正态分布时,D-K选择模型的参数估计是否具有稳健性;(2)追踪数据中含有不同缺失机制的数据,且目标变量不满足正态分布时,基于增长模型的稳健极大似然(MLR)方法与 D-K选择模型相比两者是否存在差异。同时,考虑数据偏离正态的程度、数据缺失比例、样本量对不同方法的影响,并据此提供一些方法选择和使用上的建议。

3 基于增长模型的缺失数据处理方法

潜变量增长模型(Latent Growth Curve Model,LGM)是处理追踪数据的一种常用方法。该模型在结构方程模型(Structural Equation Modeling,SEM)的视角下定义发展趋势(McArdle &Epstein,1987;Meredith &Tisak,1990),通过潜变量(截距和斜率)来描述重复测量变量的发展特征。潜变量增长模型中不仅关注潜变量的均值,同时关注其方差;前者描述了整体的增长趋势,后者则代表增长趋势存在的个体差异。

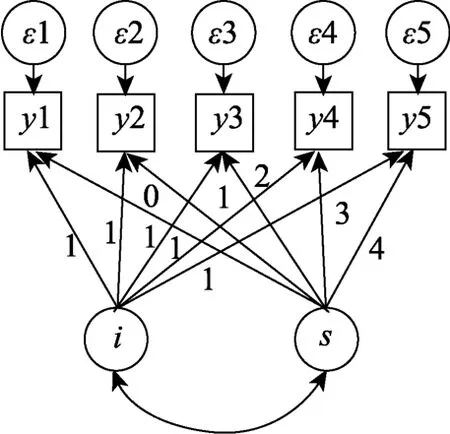
图1 潜变量增长模型

3.1 基于MAR假设的极大似然估计

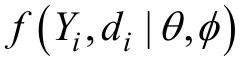
由于在MAR机制下,ML方法得到的参数估计是无偏的,而且与其他传统的处理方法(如列删除、对删除和单一插补等)相比更加有效,方法学家们认为其是一种先进的处理缺失数据的技术(“a stateof-art missing data technique”.Schafer &Graham,2002)。甚至在MCAR机制下,ML方法也会比其他处理方法产生更优良的统计量,因为它通过从观测数据中“借取”信息而使得统计检验力最大化(Enders &Bandalos,2001)。虽然理想的极大似然估计假设数据服从正态分布,但是大量的研究结果表明,非正态校正的稳健极大似然估计(robust ML;Yuan &Bentler,2000)即使在非正态的情况下,也可以得到近似无偏的结果。

3.2 Digg le-Kenward选择模型

选择模型(Selection Modeling)(Glynn,Laird,&Rubin,1986;Little,1993,1995)将数据和缺失概率的联合分布分解为边缘分布和条件分布的乘积：

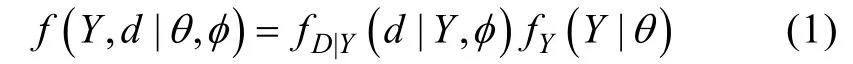
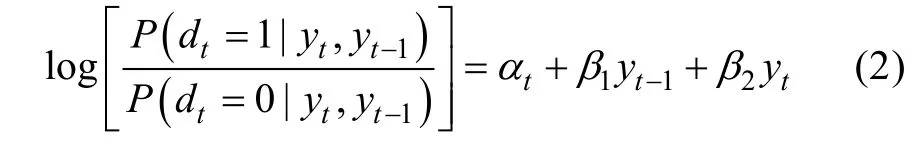
以Probit回归模型定义的MNAR缺失机制可以用公式表示为：

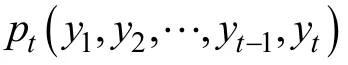
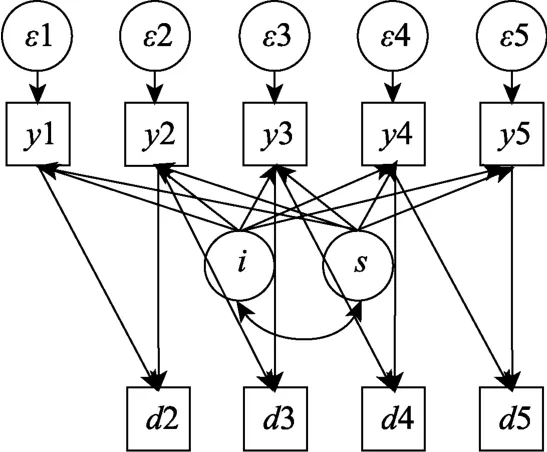
图2 Diggle-Kenward选择模型

4 研究方法

4.1 模拟设计

为了便于考察影响模型参数估计的因素,参考于以往研究者(Soullier,de La Rochebrochard,&Bouyer,2010;Yuan,Yang-Wallentin,&Bentler,2012)在模拟研究中考虑的影响因素,模拟设计如下：

(1)样本量,根据前人研究(Zhang &Willson,2006)的建议,增长模型的最小样本量不低于 50,因此取100、300、500、1000四个水平,依次代表从小到大的样本量。

(2)数据永久缺失比例,取5%、10%、20%、40%四个水平,依次代表由少至多的永久缺失数量。设定在某时间点永久缺失的个体在随后时间点均保持缺失,则该比例代表在此时间点剔除此前已退出的个体后,剩余的个体中发生永久缺失的比例。

(3)目标变量分布的偏态程度,取正态、轻微偏态、中度偏态和严重偏态四个水平。设定轻微偏态分布的偏度为0.5,峰度为3;中度偏态的偏度为2,峰度为12;严重偏态的偏度为3,峰度为30。

(4)考虑MNAR和MAR两种缺失机制。

研究共包括4×4×4×2=128种实验处理,每种实验处理重复 500次。应用 Mplus软件(Muthén,&Muthén,2007)进行分析。分析所用的语句见附录1和附录2。

4.2 数据生成与分析

本研究采用 R语言生成符合不同模型假设并带有不同缺失模式的纵向数据集。数据生成过程如下：

第一步：生成完整的纵向数据集。

模拟的数据集代表对

n

个被试重复测量

t

(

t

=5)次的追踪研究,每次测量得到一个观测值。采用潜变量增长模型来生成满足目标变量分布特点的每个被试在各个时间点的观测值

y

,其中,

j

=1,…,

t

。对增长模型中的参数设定如下：截距

i

服从正态分布,其均值为−1,方差为 0.50;斜率 s服从正态分布,其均值为0.5,方差为0.02;残差之间相互独立,且服从正态分布,其均值为0,5次测量残差的方差分别为：0.50,0.48,0.42,0.32,0.18。其中非正态数据的生成借助于广义Lambda分布生成(Headrick &Mugdadi,2006)。

第二步：生成永久缺失模式的数据集。

对于永久缺失模式为 MNAR的情况,考查其符合D-K选择模型假设下的缺失机制,即目标变量在某一时间点的缺失概率同时受当次观测值和前一次观测值的影响。对于永久缺失模式为MAR的情况,考查符合 ML方法假设下的缺失机制,即目标变量在某一时间点的缺失概率与上一时间点的观测值有关,而与当次观测值无关。具体来说,在D-K选择模型的 MNAR机制假设下,使得目标变量在某一时间点的缺失概率与当次观测值的大小成正比例关系,与上一时间点的观测值成反比例关系;在 ML方法的 MAR机制假设下,使得目标变量在某一时间点的缺失概率与上一时间点的观测值大小成反比例关系,而与当次观测值无关。

4.3 评价标准

对于不同的处理方法的评价标准,主要从参数估计精度和 95%置信区间对真值的覆盖比率两个方面来进行比较和评价。

(1)误差均方根(Root Mean Square Error,RMSE)。RMSE描述了参数估计值与真值之间的差异大小,其值越小表示得到的参数估计值与真值的偏差越小。RMSE的计算公式为：

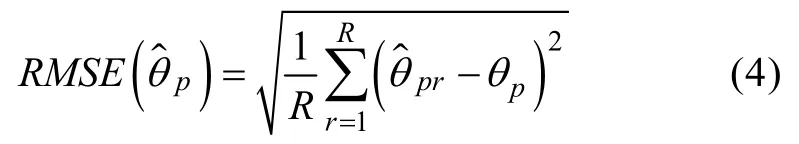
(2)95%置信区间对真值的覆盖比率(Coverage Probability,CP)。该指标体现了估计的准确性,能在一定程度上反映参数估计精度和对应的标准误估计值的情况。其计算公式为：

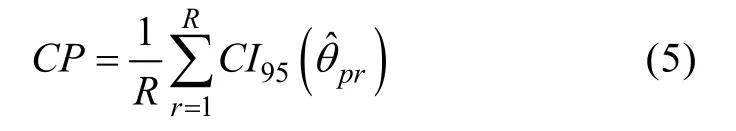
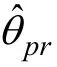
5 研究结果

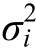
5.1 参数估计精度

在缺失机制为 MAR的情况下,基于 MAR的ML方法得到的参数估计的精度都略好于D-K选择模型;而在缺失机制为 MNAR的情况下,基于MNAR的D-K选择模型都优于ML方法。这主要是由于MAR的缺失机制更符合ML方法对缺失机制的假设,而MNAR的机制更符合D-K选择模型对数据缺失机制的假设。

(1)截距均值的估计精度及影响因素

从图3的结果可以看出,两种缺失模式下,对于两种处理缺失数据的方法,随着样本量的增大,参数估计的精度越来越高。从图3(a)和图3(b)可以看出,在MAR缺失模式下,D-K选择模型和ML方法不存在差异,截距均值的估计精度不受缺失比例大小的影响;而在MNAR的缺失模式下,D-K选择模型和ML方法存在差异,且随着缺失比例的增加,两种方法之间的差异越来越大。从图3(c)和图3(d)可以看出,在 MAR缺失模式下,截距均值的估计精度方法间不存在差异,也不受目标变量偏态程度的影响;而在MNAR的缺失模式下,两种方法存在差异,但差异程度的大小不受目标变量偏态程度影响。综合图3的结果,对于截距均值的估计,D-K选择模型的参数估计精度即使在MAR缺失机制下仍具有稳健性,而对于ML方法,在MNAR缺失机制下,只有缺失比例较小(低于 10%)时,参数估计具有稳健性。两种方法对截距均值的估计精度均不受目标变量偏态程度的影响。

(2)斜率均值的估计精度及影响因素

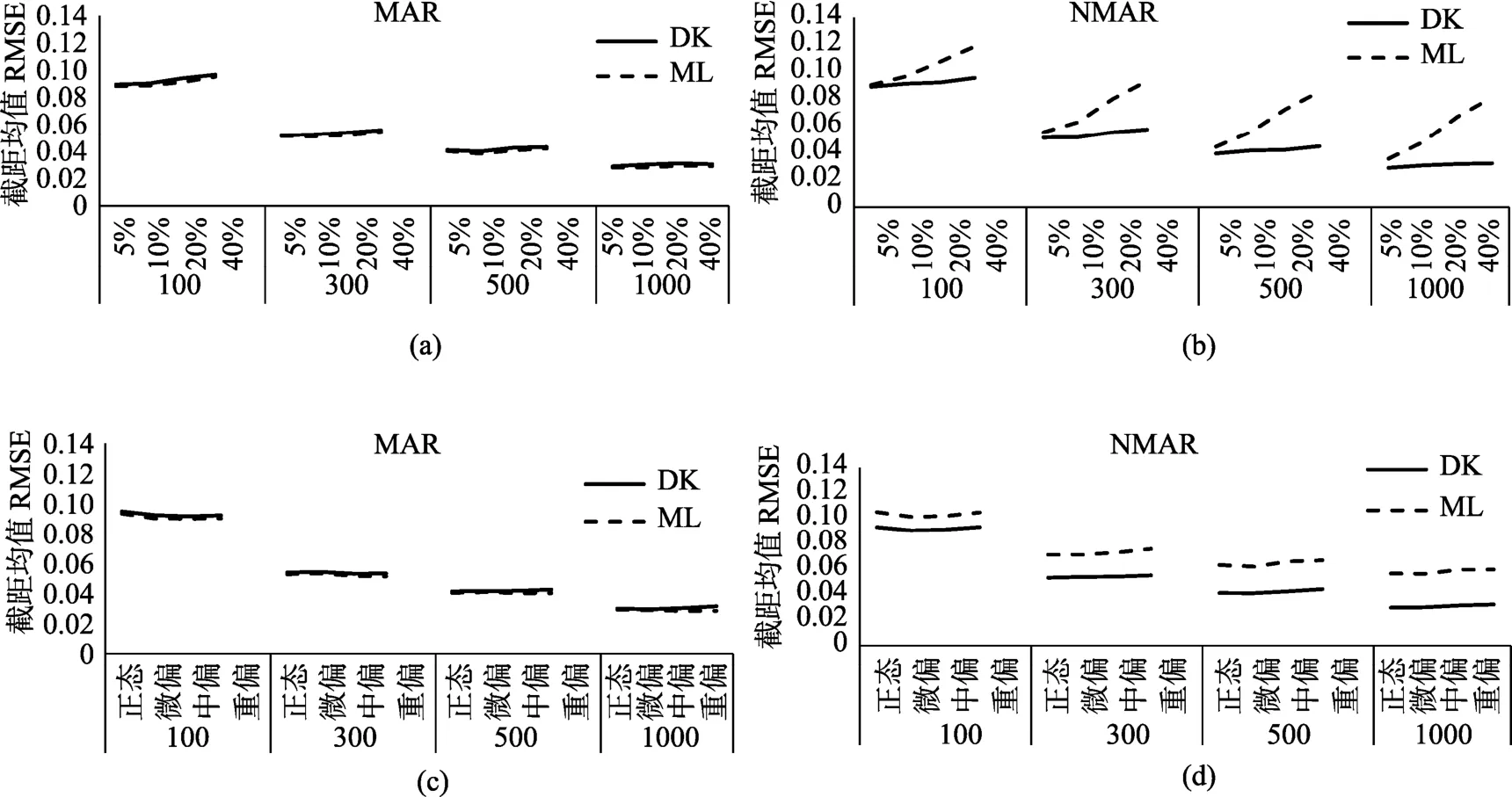
图3 截距均值估计精度及其影响因素

图4结果表明,对于斜率均值的估计,两种方法间存在差异,MAR缺失机制下,ML方法优于D-K选择模型,MNAR缺失机制下,D-K选择模型优于ML方法。

从图4(a)和图4(b)可以看出,无论那种缺失机制,随着缺失比例的增加,两种方法的差异增大。但在 MAR缺失机制下,随着样本量的增大,两种方法的差异有减小的趋势,MAR缺失比例较大时,随着样本量的增加两种方法估计的精度均越来越高,且两种方法之间的差异越来越小。在MNAR缺失机制下,随着样本量的增加D-K选择模型估计的精度越来越高,而随着样本量的增大ML方法估计的精度并没有明显的改变,且两种方法之间的差异随着样本量的增大越来越大。这说明在 MNAR缺失机制下对于斜率均值的估计,当缺失比例较大时即使增大样本量ML方法的估计精度依然很低。

从图4(c)和图4(d)可以看出,无论那种缺失机制,ML方法估计的精度几乎不受目标变量偏态程度的影响,而D-K选择模型随着目标变量偏态程度的增加,估计精度有下降的趋势。在 MAR缺失机制下,随着目标变量偏离正态分布程度的增加两种方法之间的差异增大;同时,随着样本量的增加,D-K选择模型估计精度增加,两种方法之间的差异减小。在MNAR缺失机制下,不论样本量大小ML方法的估计精度都较低;D-K选择模型对斜率均值估计精度受到目标变量分布偏态程度的影响,当分布偏态程度增加时,D-K选择模型估计精度变差。总体来讲在 MNAR缺失机制下,无论目标变量偏离正态分布的程度大小,即使增大样本量也不能有效提高ML方法的精度;D-K选择模型对斜率均值的估计精度受目标变量分布偏态程度的影响。

(3)截距方差的估计精度及影响因素

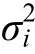
(4)斜率方差的估计精度及影响因素

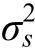
5.2 95%置信区间对真值的覆盖比率

使用正态分布的方法构建各增长参数的均值和方差估计的95%置信区间。表1分别给出不同模拟条件下两种方法得到的95%置信区间对真值的覆盖比率。

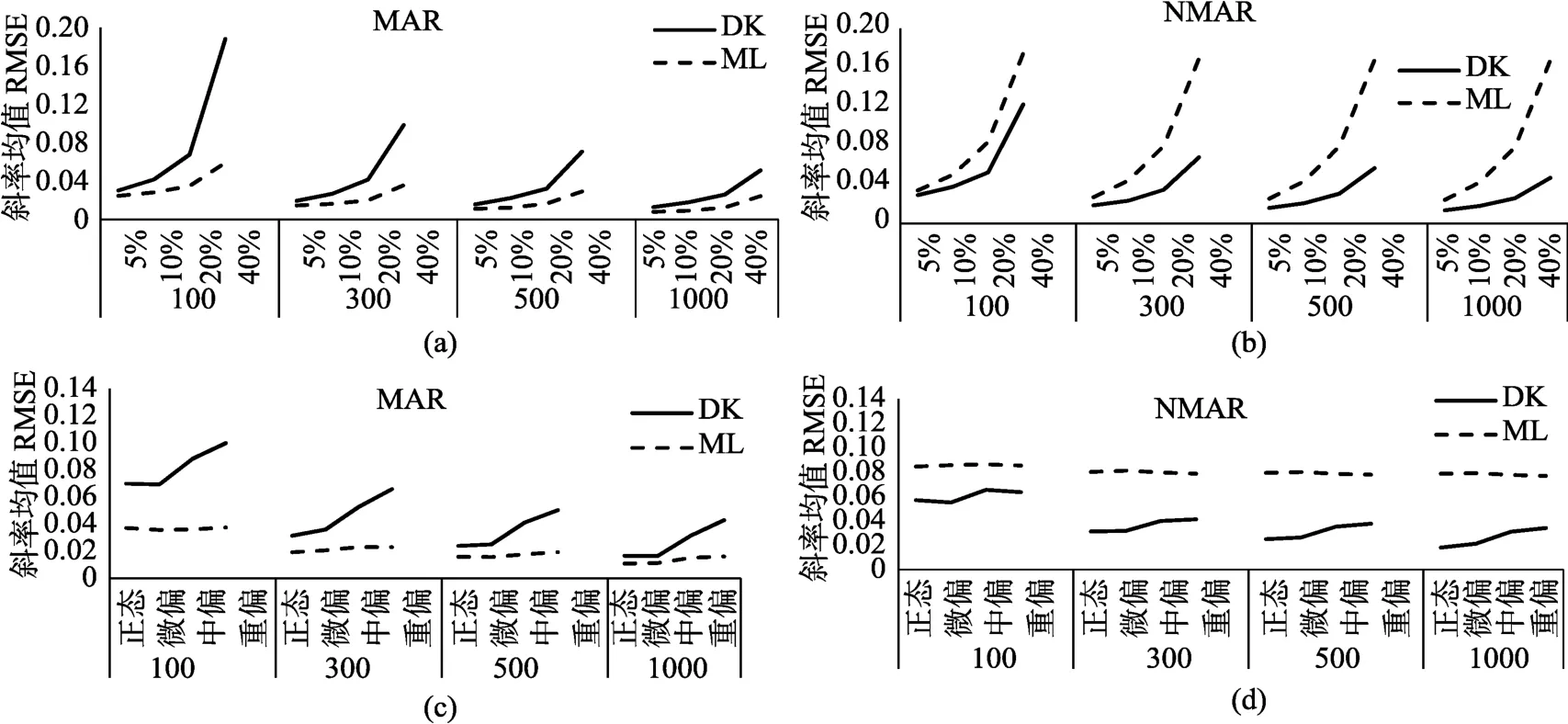
图4 斜率均值估计精度及其影响因素

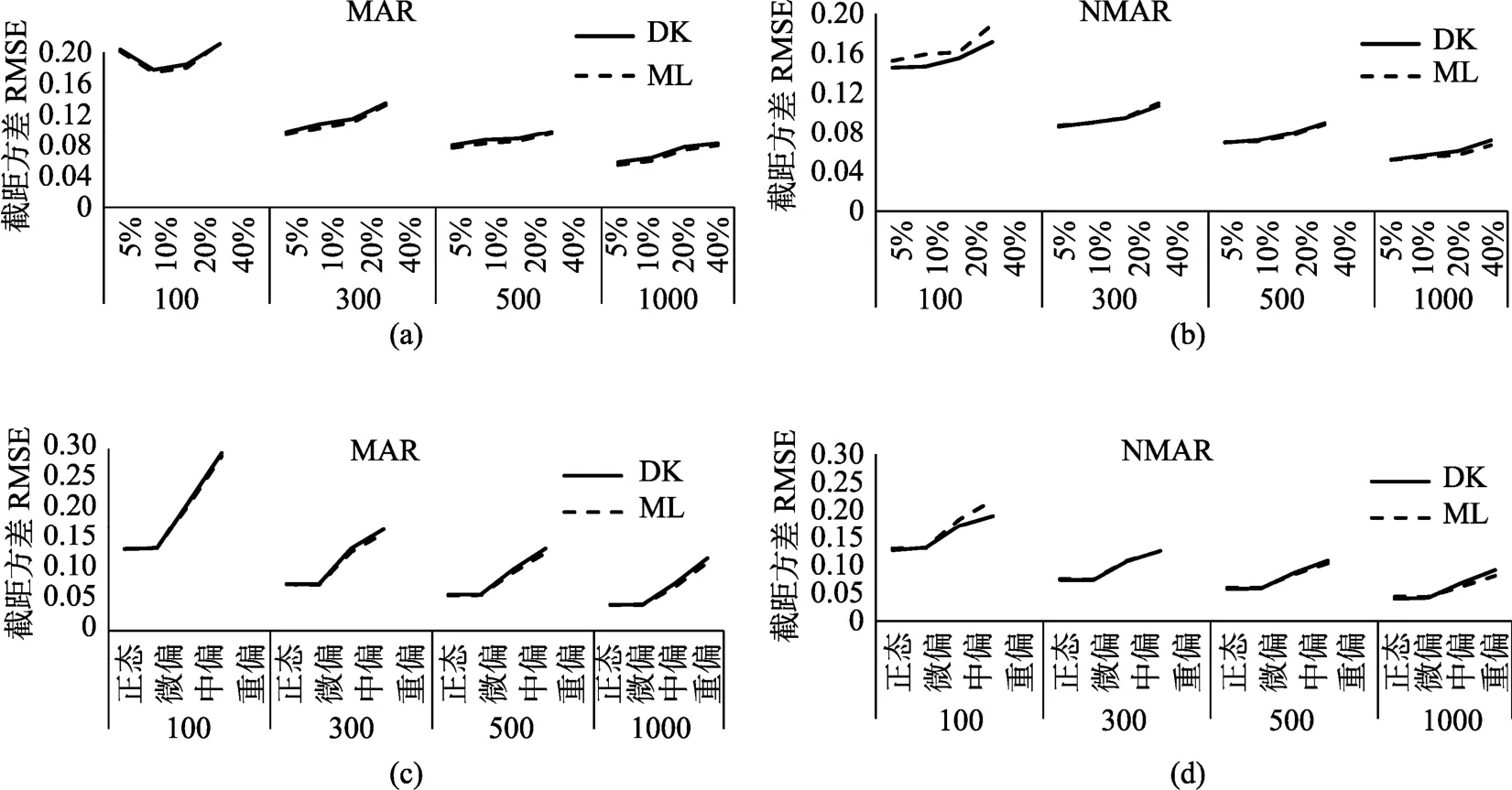
图5 截距方差估计精度及其影响因素

图6 斜率方差估计精度及其影响因素

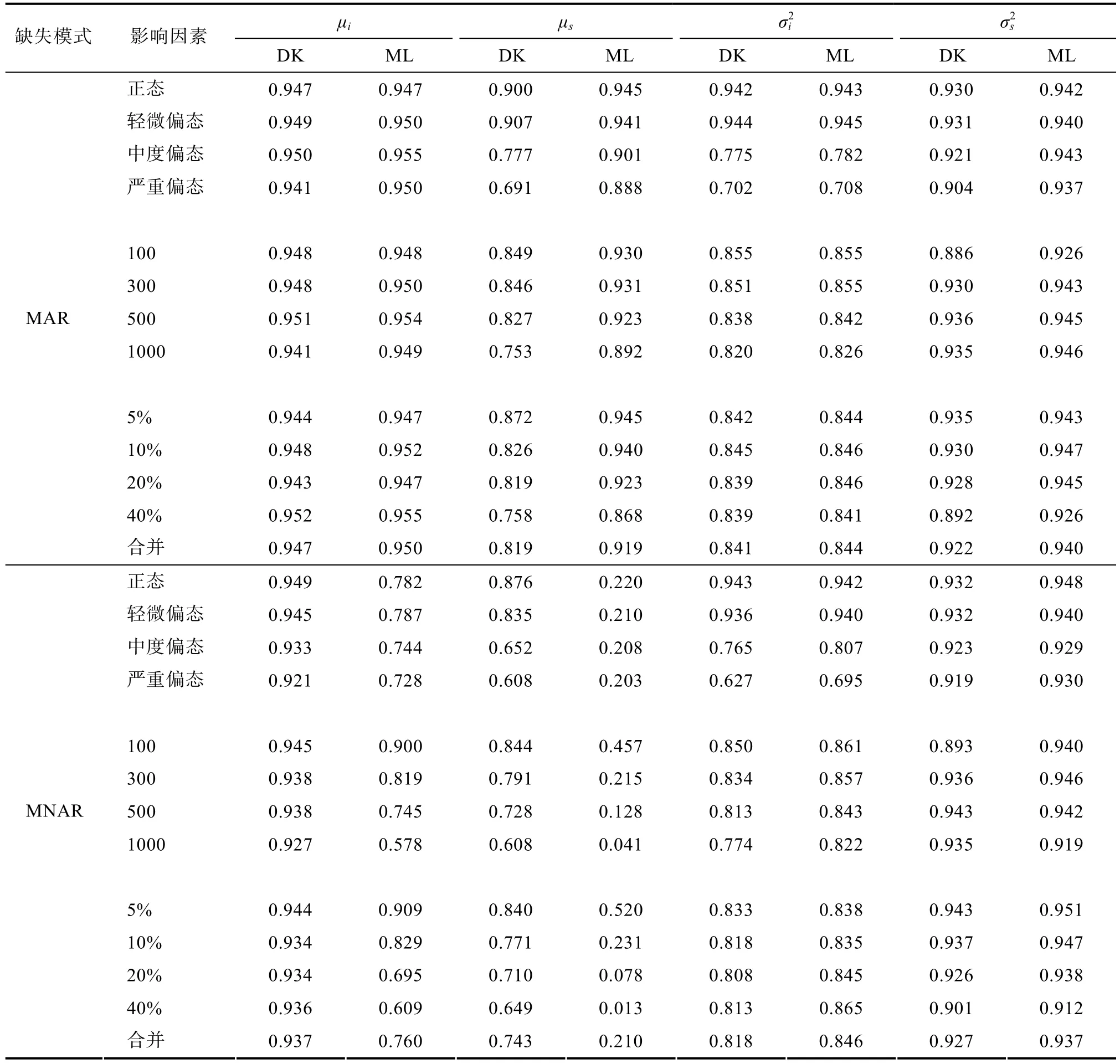
表1 95% 置信区间覆盖比率

对于截距均值的估计,在 MAR缺失机制下,两种方法得到的 95%置信区间覆盖比率差异很小;在MNAR缺失机制下,95%置信区间覆盖比率ML方法远低于D-K选择模型。在MAR下,ML方法和D-K选择模型几乎不受样本量、目标变量偏态程度和缺失比例的影响。而在MNAR下,随着分布偏态程度的增大,各方法得到的95%置信区间对真值的覆盖比率均有下降的趋势,但下降幅度不大。D-K选择模型几乎不受样本量和缺失比例的影响,但是ML方法随着样本量增大和缺失比例的增加,置信区间覆盖比率显著下降。

对于斜率均值的估计,在 MAR缺失机制下,ML方法优于D-K选择模型;在MNAR缺失机制下,ML方法得到的 95%置信区间覆盖比率远远低于MAR缺失机制下D-K选择模型。随着偏态程度增大,D-K选择模型和ML方法得到的95%置信区间覆盖比率有所降低,D-K选择模型的下降速度较明显,而ML方法下降不明显。在MNAR缺失机制下,随着偏态程度增大,D-K选择模型得到的95%置信区间覆盖比率有明显的降低,ML方法得到的结果虽有下降趋势但相对很小。随着样本量增大和缺失比例的增加,两种方法得到的95%置信区间覆盖比率均有下降的趋势。但是在MAR缺失模式下D-K选择模型受样本量和缺失比例的影响更大;而在MNAR缺失模式下,ML方法受样本量和缺失比例的影响更大。

对于斜率方差的估计,两种缺失机制下,两种方法得到的置信区间覆盖比率几乎没有差异。两种方法得到的 95%置信区间覆盖比率几乎不受目标变量分布偏态程度、样本量和缺失比例的影响。

6 讨论与建议

6.1 讨论

本文重点解决了三个方面的问题,一是在MAR缺失机制下,基于MNAR的D-K选择模型是否可以得到与ML方法近似的结果;二是在MNAR缺失机制下,基于MAR的ML方法是否可以得到与 D-K选择模型近似的结果;三是在目标变量正态分布的假设不满足时,不同缺失机制下两种方法是否具有稳健性。

(1)基于MAR的ML方法与基于MNAR的D-K选择模型的比较

无论是从参数估计的精度还是从 95%置信区间对真值的覆盖比率,在 MAR的缺失机制下基于MAR的ML方法得到了比D-K选择模型更优的结果,而在MNAR的缺失机制下基于MNAR的D-K选择模型的结果优于ML方法。

在 MAR的缺失机制下,对于潜变量增长模型关心的参数截距均值、截距方差和斜率方差这3个参数,两种方法得到的差异很小,尤其是在大样本量的情况下。这就说明即使数据是MAR的缺失机制,采用D-K选择模型对截距均值、截距方差和斜率方差的估计也不会带来非常严重的偏差,95%置信区间的覆盖比率的结果也说明了两种方法的差异不大;对于斜率的均值,两种方法存在差异,但是当样本量较大时,两种方法的差异逐渐减小,也就是说,在大样本的情况下,D-K选择模型相对于MAR机制的缺失数据,对斜率均值的估计具有一定的稳健性,不过值得注意的是此时得到的95%置信区间的覆盖比率略低于 ML方法。ML方法在MAR下得到较好的参数估计结果的结论与以往这一领域的研究所得到的结论一致,样本量和缺失比例的影响也得到了相似的结论(Enders &Bandalos,2001,2011a;Yuan,Yang-Wallentin,&Benter,2012;Lu,Zhang,&Cohen,2013)。

在 MNAR的缺失机制下,对于潜变量增长模型关心的截距方差和斜率方差这两个参数,两种方法得到的差异很小。这就说明即使数据是 MNAR的缺失机制,采用ML方法对截距方差和斜率方差的估计也不会带来非常严重的偏差,95%置信区间的覆盖比率的结果也说明了两种方法的差异不大;但是对于截距均值和斜率均值的估计,两种方法存在明显差异,且随着样本量增大,两种方法的差异越来越大。这就说明,即使在大样本的情况下,ML方法相对于 MNAR机制的缺失数据,对截距均值和斜率均值的估计仍存在较大偏差,95%置信区间的覆盖比率也可以得到类似的结论,尤其是对于斜率均值的估计;值得注意的是,当缺失比例很小时(如5%),两种方法的差异很小。综合来看,MNAR下的D-K选择模型较小受到缺失机制的影响,但是在实际应用中应结合样本量、目标变量的偏态程度和缺失比例的高低选择分析方法。Lu等(2013)和Lu和 Zhang (2014)分别基于潜变量增长模性和潜变量混合增长模型也发现缺失机制错误的定义可能会导致错误的结论,与本得到的结果一致。进一步证实了在缺失数据处理过程中选择正确模型的重要性。

(2)不同方法对目标变量分布形态的稳健性

考虑在违背模型对目标变量分布形态的假设时,各模型的估计表现如何。对于截距均值偏态程度对两种方法参数估计精度的影响均很小,对95%置信区间的覆盖比率的影响也很小。对于斜率均值,D-K选择模型在ML方法的假设下受到偏态程度的影响更大,且此时永久缺失比例与偏态程度之间存在明显的交互作用,在永久缺失比例大的情况下,其参数估计精度受偏态程度影响更敏感;与以往研究结果相同(Yuan &Lu,2008;Yuan,Yang-Wallentin,&Benter,2012;Enders &Bandalos,2001;Shin,Davison,&Long,2009),ML方法不受目标变量分布偏态程度的影响;95%置信区间的覆盖比率的结果也表明,其结果受偏态程度的影响,偏态程度越大,真值置信区间覆盖比率越低。对于截距方差的估计,各方法受到偏态程度的影响都较大,且样本量与偏态程度之间均存在显著的交互作用,在样本量小的情况下,得到的参数估计精度受偏态程度的影响更敏感。对于斜率方差的估计,MAR缺失机制下,D-K选择模型受偏态程度的影响最明显,且样本量与偏态程度之间存在明显的交互作用,当样本量小的时候,其参数估计精度受偏态程度的影响更敏感。而ML方法仅在 MNAR缺失机制下轻微受偏态程度的影响。总体来讲,D-K选择模型更容易受到目标变量分布偏态程度的影响,在样本量较大时,偏态程度的影响会减弱,尤其是对于截距均值、截距方差和斜率方差的估计结果。正如 Muthén等(2011)指出的对于非随机缺失的数据,由于缺失机制依赖于变量的分布,参数估计结果就会更多的依赖正态性的条件。

对于缺失数据处理模型的选择,应该综合考虑多种情况。其一,如果不能保证缺失数据的机制为MAR,则应注意到,非随机缺失的处理方法会依赖于目标变量的分布的这一结论,可以通过一系列的转换将其尽量转换为正态分布。其二应尽量让数据的缺失机制接近于 MAR,主要是因为 ML方法在MAR缺失机制下,即使对于非正态的数据也可以得到一致的参数估计结果Yuan和Lu (2008)。但是在实际应用中,往往很难验证数据的缺失机制是MAR,以往研究者建议在研究中尽量包含较多的变量个数,以便使得缺失数据的机制接近 MAR,二阶段的ML方法也是常用的方法(Graham,2003)。Yuan和Lu (2008)的研究表明,如果目标变量服从的分布未知或非正态,两阶段的ML方法是一个明智的选择。同时,也可以采用多个模型对数据进行分析,采用一系列模型拟合的指标,如 AIC,BIC,CAIC,BIC和DIC帮助选择合适的模型,具体内容可以参考Lu等(2013)以及Lu和Zhang (2014)的研究。

6.2 建议

由于MNAR缺失机制的理论假设较MCAR和MAR而言更为复杂,因此在实际应用中对 MNAR机制缺失数据处理方法的选择更要慎重。对于含有缺失值的研究数据,在数据处理过程中要充分了解可能造成数据缺失的各种原因,遵循一定的分析过程对数据做全面的分析和了解。结合模拟研究的结果,本文建议在进行敏感性分析时应同步注意考虑目标变量分布的偏态程度、缺失比例及样本量的大小可能对参数估计造成的影响,基于此建议处理含有缺失的追踪数据时,采用以下的处理步骤：

(1)首先检验目标变量是否服从正态分布,如果不服从正态分布,且偏离正态分布的程度为中等或较严重,则需要通过一些转换将其转换为正态分布,常用的转换方法有对数转换、指数幂转换等。

(2)检查数据的缺失模式。目前仅有完全随机缺失(MCAR)机制可以通过检验确定,方法包括进行一系列独立的t检验(Dixon,1988)、Little的MCAR检验(Little,1988)等。如果确信数据的缺失机制为MCAR,则可以采用基于完全随机缺失的传统处理方法,可参考Little和Rubin (2002)、Enders (2010,2011a)等人的介绍。

(3)如果不确定数据的缺失机制为 MCAR,检验缺失比例的高低,如果缺失比例不超过 10%,根据模型省简的原则,则可以采用基于 MAR的 ML方法。

(4)如果不确定数据的缺失机制为 MCAR,根据已有的研究或经验判断可能会存在非随机缺失,且数据缺失的比例较高,则需要对数据进行敏感性分析(sensitivity analysis)(Carpenter,Kenward,&White,2007;Graham,Hofer,Donaldson,MacKinnon,&Schafer,1997;Jamshidian &Yuan,2013;Moreno-Betancur &Chavance,2016)。众多方法学家建议研究者应用不同的模型或方法对可能含有 MNAR机制缺失的数据进行分析,检查不同方法下结果的差异(Muthén et al.,2011)。结合本研究结果,建议对带有缺失的数据分别采用MAR假设下方法(如ML方法)和 MNAR假设下的基于模型的方法(如 D-K选择模型,模式混合模型等)进行分析。

(5)将不同方法得到的结果进行比较,结合模型拟合指标(AIC,BIC,CAIC,BIC和DIC)选择一个最合理的假设对其数据的分析结果进行解释说明：如果结论在两类方法间一致,则认为选择MAR下的分析结果进行呈现也是可靠的;如果 MNAR假设下得到的结论与 MAR假设下的结论不一致,那么认为MNAR下的结果更可信。

(6)即使是基于 MNAR机制的分析,也存在不同的模型,不同模型的假设和分析结果若存在较大差异,则需要根据理论的进一步分析做出判断。

6.3 研究局限性

本研究主要探讨了MAR缺失机制假设下ML方法与MNAR缺失机制假设下D-K选择模型的比较,对于追踪研究中非随机缺失数据假设下的处理模型有多个(如模式混合模型),并且这些模型也有不同程度的拓展。本研究未能就更多的 MNAR缺失机制下的处理方法进行比较,在未来的研究中,可以进一步比较用于处理 MNAR缺失机制的不同模型间的比较。另外,本研究基于简单的 LGM 模型,在后续研究中可以考虑更复杂的基本模型,如存在潜类别的混合增长模型情境下,不同缺失值处理方法的比较。同时,在估计方法上,也应进一步考虑更多的方法,如二阶段ML方法和贝叶斯方法。

7 研究结论

(3)永久缺失比例是影响模型参数估计精度的主要因素;样本量增大会提高参数估计精度;偏态程度与永久缺失比例、偏态程度与样本量之间存在一定的交互作用。

Albert,P.S.,&Follman,D.A.(2009).Shared-parameter models.In G.Fitzmaurice,M.Davidian,G.Verbeke,&G.Molenberghs (Eds.),

Longitudinal data analysis

(pp.433−452).Boca Raton:Chapman &Hall/CRC Press.Beunckens,C.,Molenberghs,G.,Verbeke,G.,&Mallinckrodt,C.(2008).A latent-class mixture model for incomplete longitudinal Gaussian data.

Biometrics,64

(1),96−105.Carpenter,J.R.,Kenward,M.G.,&White,I.R.(2007).Sensitivity analysis after multiple imputation under missing at random:A weighting approach.

Statistical Methods in Medical Research,16

(3),259−275.Diggle,P.,&Kenward,M.G.(1994).Informative drop-out in longitudinal data analysis.

Applied Statistics-Journal of the Royal Statistical Society Series C,43

(1),49−93.Dixon,W.J.(1988).

BMDP statistical software manual:To accompany the 1988 software release

.California:University of California Press.Enders,C.K.(2011a).Analyzing longitudinal data with missing values.

Rehabilitation Psychology,56

(4),267−288.Enders,C.K.(2011b).Missing not at random models for latent growth curve analyses.

Psychological Methods,16

(1),1−16.Enders,C.K.(2010).

Applied missing data analysis

.New York:The Guilford Press.Enders,C.K.,&Bandalos,D.L.(2001).The relative performance of full information maximum likelihood estimation for missing data in structural equation models.

Structural Equation Modeling,8

(3),430−457.Glynn,R.J.,Laird,N.M.,&Rubin,D.B.(1986).Selection modeling versus mixture modeling with nonignorable nonresponse.In H.Wainer (Ed.),

Drawing inferences from self-selected samples

(pp.115−142).New York:Springer.Graham,J.W.(2003).Adding missing-data-relevant variables to FIML-based

structural equation models.Structural Equation Modeling,10

,80–100.Graham,J.W.,Hofer,S.M.,Donaldson,S.I.,MacKinnon,D.P.,&Schafer,J.L.(1997).Analysis with missing data in prevention research.In K.J.Bryant,M.Windle,&S.G.West (Eds.),

The science of prevention:Methodological advances from alcohol and substance abuse research

(pp.325−366).Washington,DC,US:American Psychological Association.Headrick,T.C.,&Mugdadi,A.(2006).On simulating multivariate non-normal distributions from the generalized lambda distribution.

Computational Statistics &Data Analysis,50

(11),3343−3353.Heckman,J.J.(1976).The common structure of statistical models of truncation,sample selection and limited dependent variables and a simple estimator for such models.

Annals of Economic and Social Measurement,5

(4),475−492.Jamshidian,M.,&Yuan,K.H.(2013).Data-driven sensitivity analysis to detect missing data mechanism with applications to structural equation modelling.

Journal of Statistical Computation and Simulation,83

,1344−1362.Little,R.J.A.(1988).A test of missing completely at random for multivariate data with missing values.

Journal of the American Statistical Association,83

(404),1198−1202.Little,R.J.A.(1993).Pattern-mixture models for multivariate incomplete data.

Journal of the American Statistical Association,88

(421),125−134.Little,R.J.A.(1995).Modeling the drop-out mechanism in repeated-measures studies.

Journal of the American Statistical Association,90

(431),1112−1121.Little,R.J.A.,&Rubin,D.B.(2002).

Statistical analysis with missing data

(2nd ed.).Hoboken,NJ:Wiley.Lu,Z.Q.,Zhang,Z.Y.,&Cohen A.(2013).Bayesian methods and model selection for latent growth curve models with missing data.In R.E.Millsap,L.A.van der Ark,D.M.Bolt,&C.M.Woods (Eds.),

New developments in quantitative psychology

(pp.275−304).New York:Springer.Lu,Z.Q.,&Zhang,Z.Y.(2014).Robust growth mixture models with non-ignorable missingness:Models,estimation,selection,and application.

Computational Statistics &Data Analysis,71

,220−240.McArdle,J.J.,&Epstein,D.(1987).Latent growth curves within developmental structural equation models.

Child Development,58

,110−133.Meredith,W.,&Tisak,J.(1990).Latent curve analysis.

Psychometrika,

55(1),107−122.Moreno-Betancur,M.,&Chavance,M.(2016).Sensitivity analysis of incomplete longitudinal data departing from the missing at random assumption:Methodology and application in a clinical trial with drop-outs.

Statistical Methods in Medical Research,25

(4),1471–1489.Muthén,B.,&Masyn,K.(2005).Discrete-time survival mixture analysis.

Journal of Educational and Behavioral Statistics,30

(1),27−58.Muthén,B.,Asparouhov,T.,Hunter,A.,&Leuchter,A.(2011).Growth modeling with non-ignorable dropout:Alternative analyses of the STAR*D antidepressant trial.

Psychological

Methods,16

(1),17−33.Muthén,L.K.,&Muthén,B.O.(2007).

Mplus user’s guide

(5th ed.).Los Angeles,CA:Muthén &Muthén.Power,R.A.,Muthén,B.,Henigsberg,N.,Mors,O.,Placentino,A.,Mendlewicz,J.,… Uher,R.(2012).Nonrandom dropout and the relative efficacy of escitalopram and nortriptyline in treating major depressive disorder.

Journal of Psychiatric Research,46

(10),1333−1338.Rotnitzky,A.(2009).Inverse probability weighted methods.In G.Fitzmaurice,M.Davidian,G.Verbeke,&G.Molenberghs(Eds.),

Longitudinal data analysis

(pp.453–476).Boca Raton,FL:Chapman &Hall.Roy,J.(2003).Modeling longitudinal data with nonignorable dropouts using a latent dropout class model.

Biometrics,59

(4),829−836.Schafer,J.L.(2003).Multiple imputation in multivariate problems when the imputation and analysis models differ.

Statistica Neerlandica,57

(1),19–35.Schafer,J.L.,&Graham,J.W.(2002).Missing data:Our view of the state of the art.

Psychological Methods,7

(2),147−177.Shin,T.,Davison,M.L.,&Long,J.D.(2009).Effects of missing data methods in structural equation modeling with nonnormal longitudinal data.

Structural Equation Modeling:A Multidisciplinary Journal,16

,70−98.Soullier,N.,de La Rochebrochard,E.,&Bouyer,J.(2010).Multiple imputation for estimation of an occurrence rate in cohorts with attrition and discrete follow-up time points:A simulation study.

BMC Medical Research Methodology,10

,79.Wu,M.C.,&Carroll,R.J.(1988).Estimation and comparison of changes in the presence of informative right censoring by modeling the censoring process.

Biometrics,44

(1),175−188.Ye,S.J.,Tang,W.Q.,Zhang,M.Q.,&Cao,W.C.(2014).Techniques for missing data in longitudinal studies and its application.

Advances in Psychological Science,22

(12),1985−1994.[叶素静,唐文清,张敏强,曹魏聪.(2014).追踪研究中缺失数据处理方法及应用现状分析.

心理科学进展,22

(12),1985−1994.]Yuan,K.H.,&Bentler,P.M.(2000).Three likelihood-based methods for mean and covariance structure analysis with nonnormal missing data.

Sociological Methodology,30

(1),165−200.Yuan,K.H.,&Lu,L.(2008).SEM with missing data and unknown population distributions using two-stage ML:Theory and its application.

Multivariate Behavioral Research,43

,621−652.Yuan,K.H.,Yang-Wallentin,F.,&Bentler,P.M.(2012).ML versus MI for missing data with violation of distribution conditions.

Sociological Methods &Research,41

(4),598−629.Zhang,D.,&Willson,V.L.(2006).Comparing empirical power of multilevel structural equation models and hierarchical linear models:Understanding cross-level interactions.

Structural Equation Modeling,13

(4),615−630.

附录1：ML方法的Monte Carlo 模拟的语句

TITLE:

ML-mnar-mar-n-40001000

DATA:

FILE=mnarmar40001000replist.dat; !指定每种模拟条件下的500个数据集文件名列表;

TYPE=MONTECARLO;!指定了分析类型为Monte Carlo模拟研究;

VARIABLE:

NAMES=m1-m5 y1-y5;

USEVARIABLES=y1-y5;

MISSING=ALL (999);

ANALYSIS:

ESTIMATOR=ML;

MODEL:

i s|y1@0 y2@1 y3@2 y4@3 y5@4;

i WITH s*0;

i*0.5 s*.02;

[i*-1 s*0.5];

y1*.5 y2*.48 y3*.42 y4*.32 y5*0.18;

SAVEDATA:

RESULTS are ml40201000results.dat;

附录2： D-K 选择模型的Monte Carlo 模拟的语句

TITLE:

DK-mnar-mar-n-40201000

DATA:

FILE=mnarmar40201000replist.dat;

TYPE=MONTECARLO;

VARIABLE:

NAMES=m1-m5 y1-y5;

USEVARIABLES=y1-y5 d2-d5;

MISSING=ALL (999);

CATEGORICAL=d2-d5;

DATA MISSING:

NAMES=y1-y5;

TYPE=SDROPOUT;

BINARY=d2-d5;

ANALYSIS:

ESTIMATOR=ML;

LINK=PROBIT;

ALGORITHM=INTEGRATION;

INTEGRATION=MONTECARLO;

PROCESSORS=2;

MODEL:

i s|y1@0 y2@1 y3@2 y4@3 y5@4;

i WITH s*0;

i*0.5 s*.02;

[i*-1 s*0.5];

y1*.5 y2*.48 y3*.42 y4*.32 y5*0.18;

[d2$1*1.1134 d3$1*1.3506 d4$1*1.5745 d5$1*1.7842 ];

d2 on y1*-0.5 (11)

y2*1 (12);

d3 on y2*-0.5 (11)

y3*1 (12);

d4 on y3*-0.5 (11)

y4*1 (12);

d5 on y4*-0.5 (11)

y5*1 (12);

SAVEDATA:

RESULTS are dk40201000results.dat;