定弦定角问题及求最值的应用研究
杜幸元
(广东省深圳市宝安区松岗中学,广东 深圳)
在定弦定角问题中,一般的题目设置多以某个动点到一个定点的线段的长度的最大值或最小值问题为主,解决这类题型首先要熟知定弦定角的含义及性质,掌握原理解题才会更加清晰简洁。首先我们需要掌握圆的各种性质,并能够进行熟练的转化和应用,其次是观察动点的运动轨迹,一般轨迹是一段弧,然后寻找不变的张角,并找出它的补角,以此为解决问题的突破口。之后根据张角找出他所对应的定弦,三点确定一个圆,确定好圆心,以此为基础再进一步求最值。下面我们将根据例题,对问题进行具体的分析,总结相关的应用方法。
一、认真分析题目给出的条件
在解决定弦定角及求最值问题时,首先要认真分析题目给出的条件,需要掌握圆的相关概念和性质,这是解决问题的前提。将题目给出的条件与圆的性质对应起来,与定弦定角的内涵对应起来,然后再解决下一步的问题。
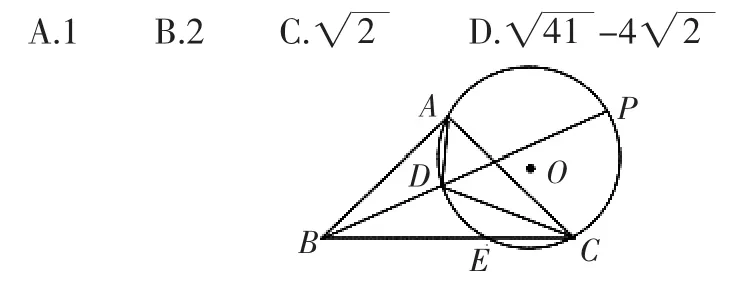
解:
因为∠CDP=∠ACB=45°
所以∠BDC°=135°(定弦定角的最值)
如图,当AD过O时,AD有最小值
因为∠BDC=135°
所以∠BOC=90°
所以△BOC为等腰直角三角形
所以∠ACO=45°+45°=90°
所以AO=5
又因为OB=OC=4
所以AD=5-4=1
二、有效运用数形结合思想
解决这类问题必须要学会数形结合,利用图形解决问题会起到事半功倍的效果。将题目中的条件在图形上表现出来,这样解题时会更加直观明了。此外很多题目之间可以互相转化,大家在练习中要注意总结相同点与不同点。
【例 2】如图,A(1,0)、B(3,0),以 AB 为直径作圆 M,射线 OF交圆O于E、F两点,C为弧AB的中点,D为EF的中点,当射线绕O点旋转时,CD的最小值为 ( )

解:连接DM
因为D是弦EF的中点
所以DM⊥EF
所以点D在以A为圆心、OM为直径的圆上运动
当CD过圆心A时,CD有最小值
连接CM
因为C为弧AB的中点
所以CM⊥AB
三、做出圆外一点与圆心的连线
在圆的定弦定角及求最值问题中,有一类题型是求圆外的一点到圆上的点的最值问题,这类问题其实是画出圆外一点与圆心的连线,延长与圆相交于两点,这两点与圆外一点的距离实际上就是最大值和最小值。
【例 3】如图,在 Rt三角形 ABC 中,∠ABC=90°,AB=4,BC=6,P是三角形ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP的长度的最小值是 ( )
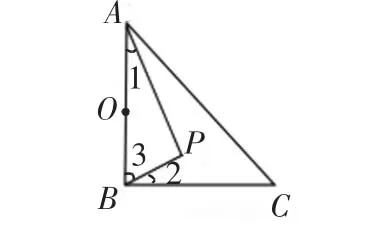
解:
因为∠ABC=90°,即:∠2+∠3=90°
又因为∠1=∠2
所以∠1+∠3=90°
所以∠APB=90。
所以∠APB在以AB为直径的圆上,
如图,圆心记为O,当CP所在直线经过圆心O时,CP最短
此时半径OB=2,BC=6
所以在Rt△OBC中,由勾股定理得:
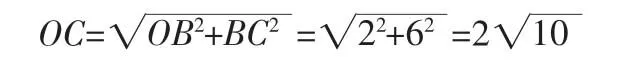
分析:这道题也可转化为求CP的长的范围,将AB看成定弦,将∠APB看成定角,看做是圆外一点经过圆心与圆的两个交点的距离。
总之,定弦定值及求最值问题都有一个固定的方法和模式,其解题思路其实是一样的,需要学生在认真分析问题的基础上,找出解决问题的关键点,找到问题的突破口,也可进行反向思考,要想求出最值,就必须具备什么样的条件,在猜测的基础上一步步找出题目给出的隐含条件,帮助解决问题。希望以上定弦定点及求最值问题的应用方法和策略能够为初中数学教师和学生起到良好的理论指导作用,帮助学生更快速、更便捷地解决这部分的问题。

