测度K-框架

张超华

(南京航空航天大学 理学院，南京 211106)

Hilbert空间中的框架概念发展到现在有着十分广泛的应用，它不仅在处理信号、压缩数据、采样等数学领域本身的学科上，而且在光学，通信工程等其它学科，都发挥了巨大作用.

Ehler结合测度和积分提出的一种比经典框架更一般的框架，并命名为测度框架，它是利用测度，建立在测度集上积分而得到的一种框架.

本文将在文献[1-3]的基础上，通过K-框架理论给出测度K-框架的定义，讨论测度K-框架与测度框架的关系，对测度K-框架的最优界利用测度框架的分析算子、合成算子以及算子K对测度K-框架的最优界进行控制，并利用算子K给出紧测度K-框架成为测度框架的等价性结论.

本文中的Hilbert空间均是可分的，I为H上的恒等算子.B(H1,H2)表示Hilbert空间H1到H2上的全体有界线性算子.简记B(H,H)为B(H).记算子F的共轭算子为F*.Ω表示Rn的非空子集，并令Μ(Ω,Β)为Ω上的全体有限正测度的集合，Β是指Ω诱导出的Borelσ-代数.

1 预备知识

定义1[2,4]设μ∈M(Ω,Β)为Rn上的测度框架，如果存在正数α,β，使得

(1)

α,β分别为框架μ的下界，上界.对式(1)，若只要求右边不等式成立，则称μ为Bessel测度;若α=β，则称μ为Rn的紧测度框架.进一步，若α=β=1，则称μ为Rn的Parseval测度框架.对于Rn的Bessel加权测度μ，称有界线性算子θμ

θμ：Rn→L2(Ω,μ),θμx=〈x,·〉Rn

(2)

(3)

(4)

这些算子在框架理论的研究中具有重要的作用.

引理1[5-6]设H，H1，H2是Hilbert空间，T1∈B(H1,H)，T2∈B(H2,H)，则下列叙述等价：

(1)R(T1)⊆R(T2);

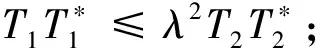
(3)存在T∈B(H1,H2)，使得T1=T2T.

引理2[7]设T∈B(H1,H2)，则T是满的充要条件为T*是下有界的，即存在正数c，对任意x∈H，均有‖T*x‖≥c‖x‖.

2 测度K-框架

定义2 设K∈B(Rn)，称μ∈M(Ω,Β)为Rn上的测度K-框架，若存在正数α,β，使

(5)

称α,β为μ的框架下界，上界.若上式中K=0，称μ为测度0-框架.另外，若将式(5)左边不等式改为等式，则称μ为Rn上的紧测度K-框架.

注1 显然Bessel测度一定是测度0-框架.设μ是Rn上的界为α,β的Bessel测度，若K=0，则K*=0，从而

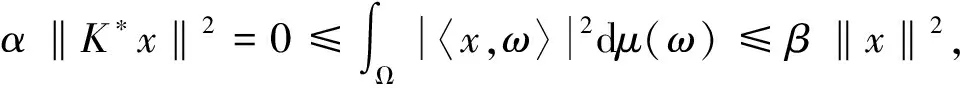
因而μ为Rn上的测度0-框架.

注2 若在式(5)中K=I，则μ为Rn上的测度框架.从而可以将测度K-框架看做是测度框架的一种推广.

定理1 设μ∈M(Ω,Β)是Rn上的Bessel加权测度，则下列等价：

(1)μ为测度K-框架，界为α,β;

(2)存在正数α,β，使得αKK*≤Sμ≤βI.

证明任取x∈Rn，由式(4)可知

(6)

另外，结论(2)成立等价于：〈αKK*x,x〉≤〈Sμ,x〉≤〈βx,x〉，∀x∈Rn.因此命题成立.证毕.

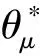
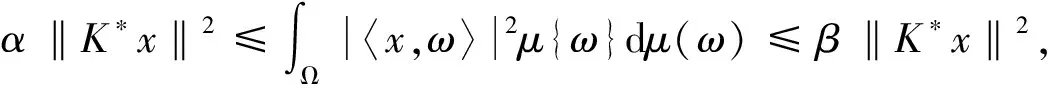
αKK*≤Sμ≤βI成立.证毕.

通过下面的讨论，我们知Rn的测度K-框架的最优下界可以由算子K和框架算子Sμ来描述.

定理3 设K∈B(Rn)且K≠0，若μ∈M(Ω,Β)是Rn的测度K-框架，那么最优下界，上界分别为λmin‖K‖-2，‖T‖2，λmin表示为Sμ的最小的不为零的特征值.

证明因为μ是Rn的测度K-框架，所以存在正数α,β，使得测度K-框架不等式(5)在Rn上成立.从而,

又因为

故α=λmin‖K‖-2是最优下界.最优上界显然.证毕.

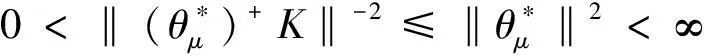
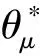
3 利用算子给出紧测度K-框架成为测度框架的等价刻画

本节着重研究测度K-框架与测度框架的关系，给出紧测度框架成为测度框架的算子的等价描述.

定理5 设K∈B(Rn)，μ∈M(Ω,Β)是Rn的测度框架，界为α,β.则μ为Rn上的测度K-框架.若K≠0，则其框架界为α‖K‖-2，β.

证明设μ∈M(Ω,Β)是Rn的测度框架，界为α,β，任取x∈Rn，

对任意K∈B(Rn)，K=0时显然符合结论;在K≠0时，则‖K*‖=‖K‖≠0，从而

‖K*x‖≤‖K*‖·‖x‖=‖K‖·‖x‖， ∀x∈Rn.

从而

‖K*x‖·‖K‖-1≤‖x‖.

因此

μ为Rn的测度K-框架，界为α‖K‖-2，β.证毕.

定理6 设Ω⊆Rn是有界的，K∈B(H)是Rn上的满射，则μ∈M(Ω,Β)为Rn的测度K-框架的一个充要条件是μ的支集生成Rn.

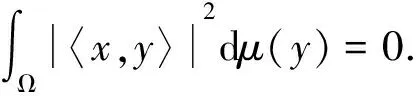
必要性.由定理5，只需证明μ是测度框架.由柯西-施瓦茨不等式,

又由有限测度μ以及Ω的有界性,得到μ为Bessel测度.定义

选择合适的算子K∈B(Rn)，我们可以由测度框架来构造一个测度K-框架.

引理3[8]若μ∈M(Ω,Β)为Rn的界为0<α≤β<∞的测度框架，且K∈B(Rn)是单的，则μ°K-1是Rn上的界为α,β‖K*‖2的测度K-框架.

证明设μ∈M(Ω,Β)为Rn的测度框架，界为α,β，任取x∈Rn,

上式表明μ°K-1是Rn上的测度K-框架.证毕.

下面利用算子K给出紧测度K-框架成为框架的等价刻画.

定理7 设K∈B(Rn)，μ∈M(Ω,Β)是Rn的紧测度K-框架，则下列叙述等价：

(1)μ是Rn的测度框架;

(2)K是满的.

证明(1)⟹(2).若μ是Rn上紧测度K-框架，其界为α1.由定义2，有

(7)

若μ是Rn的测度框架，且最优下界为α2，由定义1得

(8)

再由μ是紧测度K-框架.那么由(7)和(8)知，

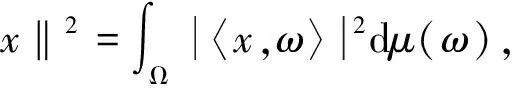
从而,

因此再利用引理2可得算子K是满的.

(2)⟹(1).设算子K为满射，由引理2可以找到正数c，使c‖x‖≤‖K*x‖，∀x∈Rn.由于μ是Rn的测度K-框架，故存在正数α,β，使得,

因此

故(1)成立.证毕.

推论1 设K∈B(Rn)可逆，则μ∈M(Ω,Β)是Rn的测度K-框架.

[1] 丁明玲，肖祥春，朱玉灿.Hilbert空间中的K-框架[J].数学学报,2014，57(6)：1090-1099.

[2] MEHLER.Random tight frames[J].Fourier Anal Appl，2012，18：1-20.

[3] 丁明玲，肖祥春，曾晓明.Hilbert空间中的紧K-框架[J].数学学报，2013，56(1)：105-112.

[4] MEHLER.Frame theory in directional statistics[J].Galanis-Statistics & Probability Letters，2011,158：1046-1051.

[5] DOUGLAS R G.On majorization，factorization and range inclusion of operators on hilbert space[J].Proc.Amer，Math.Soc.，1966，17(2)：413-415.

[6] RUDIN W.Real and complex analysis [M].Third Edition-1987-Tata McGraw-Hill Education,1987.

[7] CHRISTENSEN O.An introduction to frames and riesz bases[M].Boston：Birkhauser，2003.

[8] CHRISTENSEN O.Frames and pseudo-inverse[J].J Math Anal Appl,1995,195:401-414.